基于冗余数据分析的船舶主机控制系统传感器偶发性故障检测
2021-08-09李志闫明胜韩宝宏魏慕恒朱慧敏李奇钟
李志,闫明胜,韩宝宏,魏慕恒,朱慧敏,李奇钟*
(1. 神华中海航运(天津)有限公司,天津 300000; 2. 震兑工业智能科技有限公司,深圳 518101)
0 引言
近年来,伴随着船舶主机控制系统日益复杂化和精密化的发展趋势,构成控制系统的复杂电子电路和设备仪器的老化逐渐成为控制系统故障的重要诱因,而构成控制系统终端的众多传感器,受到包括振动、电磁干扰等恶劣的工作环境的影响,其老化速度往往明显高于线缆和其他对精度要求不甚严格的机电设备,而故障传感器返回的错误读数又会进一步导致控制系统做出错误决策,最终可能产生严重的安全事故,造成重大损失。而及时有效检测出微小故障对于降低系统损伤、减少事故发生具有重要意义[1]。
当传感器发生老化时,其故障往往表现出偶发性的特点,即故障持续时间有限,没有外部补偿故障仍可自行消失。也正因如此,偶发性故障在前期往往难以排查,而长期的风险累积又会导致严重后果。工业上通常根据经验对易损件进行定期更换,但难以在成本和安全性之间寻求平衡。
考虑到船舶控制系统通常会在同一设备上布置多个同类型传感器,其传回的数据之间往往具有较大的相关性和冗余度,如果其中某些传感器的读数和总体数据规律发生明显偏离,且这种偏离现象以一定频率重复出现,则认为发生了偶发性故障。基于这种思路,本文提出了一种能够对船舶主机控制系统的传感器偶发性故障进行准确检测的方法和系统。
1 DPCA检测模型
自Mehra[2]第一次系统探讨故障诊断技术以来,各种数据驱动的故障识别和诊断方法层出不穷,许多基于神经网络的方法在具体场景都收到了良好效果[3-5],但是为了达到理想的检测效果,往往需要用到深层的神经网络,算法往往实时性较差,需要对网络进行优化,而优化又会导致算法失去可移植性[6]。综合考虑算法的实时性和通用性,我们选择使用传统的多元统计分析方法对高维的冗余数据进行分析。
主流的多元统计分析故障诊断方法有主成分分析(Principal Component Analysis, PCA)、规范变量分析(Canonical Variable Analysis, CVA)、Fisher判别分析(Fisher Discriminant Analysis, FDA)、偏最小二乘法(Partial Least Squares, PLS)等[7]。其中尤以PCA最为常用,其结果的可解释性较强,适用于需要对模型进行机理解释的广阔工业场景。
利用主成分分析(PCA)对多传感器传回的同类型数据进行降维,可以从冗余数据中提取出关键特征,表征数据的主要规律。在工业上,利用PCA方法对数据进行降维并利用聚类方法对故障类型进行归纳和诊断是一种通用的做法,可以大大降低故障检测的复杂性[8]。PCA方法通常与某种聚类方法结合,前者提取故障特征,后者负责对故障进行分类,如与SVM结合对振动传感器的故障进行诊断[9]、与KNN相结合用于检测生化过程中的物质成分异常[10-11]、与模糊核聚类方法(KFCM)相结合,对船舶柴油机故障进行诊断[12]等。针对传感器偶发性故障,单独使用PCA用于提取特征用于后续检测即可。
虽然基于主成分分析的过程监控方法得到了广泛的应用,然而,该方法假设独立采样,即样本之间不存在时序相关性。在实际中,由于工业过程的动态特性,过程数据往往很难严格满足上述假设。对此,Ku等[13]提出,通过扩展主成分分析模型,通过将一部分时延样本纳入数据矩阵,可以构建动态主成分分析模型,对时序相关的动态过程数据进行建模。由于各传感器数据之间存在延时,即存在明显的时间相关性,所以用DPCA而不是PCA方法来判定,具有更好的准确性[14]。
我们首先采集船舶主机控制系统的传感器在正常工况下的测量样本x,k时刻的测量样本记为x(k),x(k)为m维列向量,m为传感器个数,建模过程共采集N个时刻的N组测量样本;对正常工况下的测量样本进行时延处理构造为扩增测量矩阵:

(1)中,d是时延样本长度,x(k)是时刻的测量样本的转置,k=1-d,2-d,3-d...N;将扩增测量矩阵X的各列归一化为零均值单位方差,得到规范测量矩阵Xnorm。
对规范测量矩阵的协方差矩阵S进行特征值分解,表达式为::

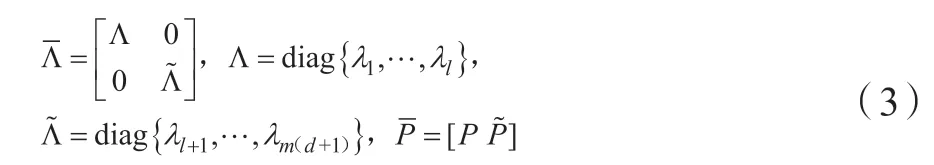
其中P是[m×(d+1)]×l阶矩阵,为主成分矩阵,由的前l列构成,为非主成分矩阵,是的第j个对角元素表示对角元素为的对角矩阵,表示对角元素为的对角矩阵;
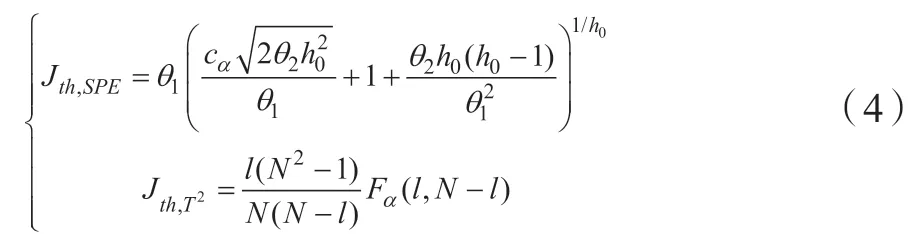
至此,我们获得了冗余数据中的主成分特征,以及相应的统计量计算参数与阈值。对于待分析的在线测量样本序列z,k时刻的测量样本记为z(k),其两种统计量的计算表达式为:

参数定义同(3)。
将在线计算出的平方预测误差SPE和霍特林T2统计量与预设阈值进行比较,若SPE≤Jth,SPE且,则船舶主机控制系统传感器无偶发性故障,否则发出预警。算法流程图如图1所示。
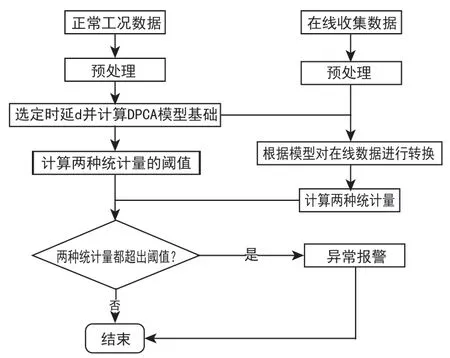
图1 故障检测流程
2 实验与结果分析
2.1 数据来源及实验流程
我们采集了本公司经营的一条二十万吨级货运船出厂后一年内的航行数据。由于船上的设备均为全新,我们取第一周的数据作为正常样本,将后半年航行的数据作为测试样本,用于检测是否存在控制系统传感器偶发性故障。其中船主机气缸安装有十六个同型号的不同位点的温度传感器(依次称为传感器1,传感器2, ,传感器16),用于记录排气温度。图2展示了其中任意选取的三个位点在出厂后第一个星期内记录的温度值。
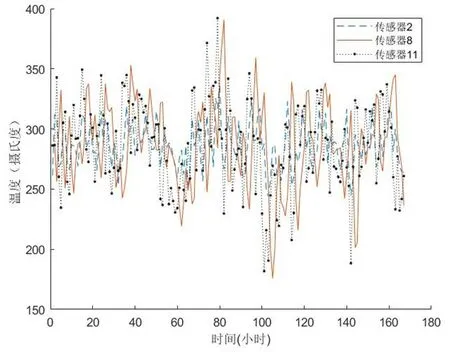
图2 三个传感器记录的正常工作数据
为了提升算法的准确性,我们将所有传感器的数据均进行去均值和方差归一化的预处理,然后用DPCA检测模型进行处理,分别取延时d为0-100的所有整数,其中d=0意味着没有任何时延,即PCA方法。而经过反复试验,d=100是一个远超出系统最大延时的边界,这一点从2.2中的结果中可以看出。
2.2 结果与分析
由于存在一个客观最大时延dmax,所以当d≥dmax时,继续增大时延不会对准确率有进一步的提升。我们以d=100时找到的所有异常作为基准,对其他各情况的准确率进行计算,得到准确率关于d的变化情况如图3所示。图4则展示了d=100时传感器1的一段数据在经DPCA处理后,得到的SPE和霍特林T2统计量及相应阈值的情况。从图中可以看出,SPE和霍特林T2统计量检测到的异常并不完全重合,实际应用中我们取二者的交集作为结果,这是考虑到偶发性故障尚不明显时并不会对船舶的航行安全造成明显影响,为了减少虚警而采用了较为保守的故障检测原则。
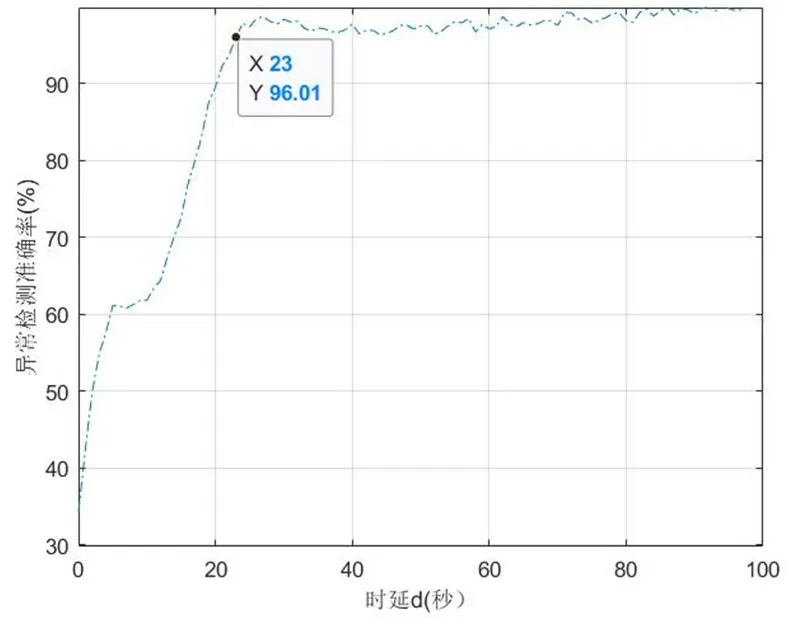
图3 检测准确率关于时延的变化关系
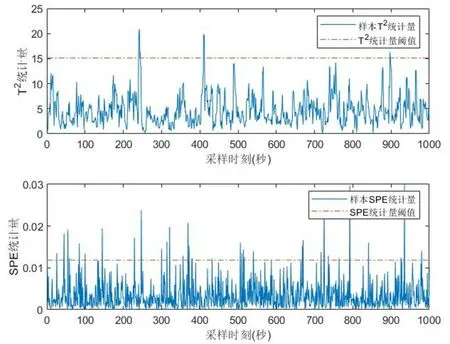
图4 利用基于DPCA的故障检测方法检测到240秒时刻前后有偶发故障发生
由图3可以估计,客观最大时延dmax≈23,随着d的增加,算法的用时也在逐渐增加,在单核CPU的前提下,其运行时间和检测准确率见表1。同时,我们也可以从算法理论层面进行对比,分别将d取值为(0,10,23,100)的情况下,16维中的前十维的特征贡献比例如图5所示。从图5中可以看出,考虑了时延之后,特征的贡献比例更加向前几维集中,这也意味着算法能更加有效地反映冗余数据的核心信息,有利于对数据的后续处理。
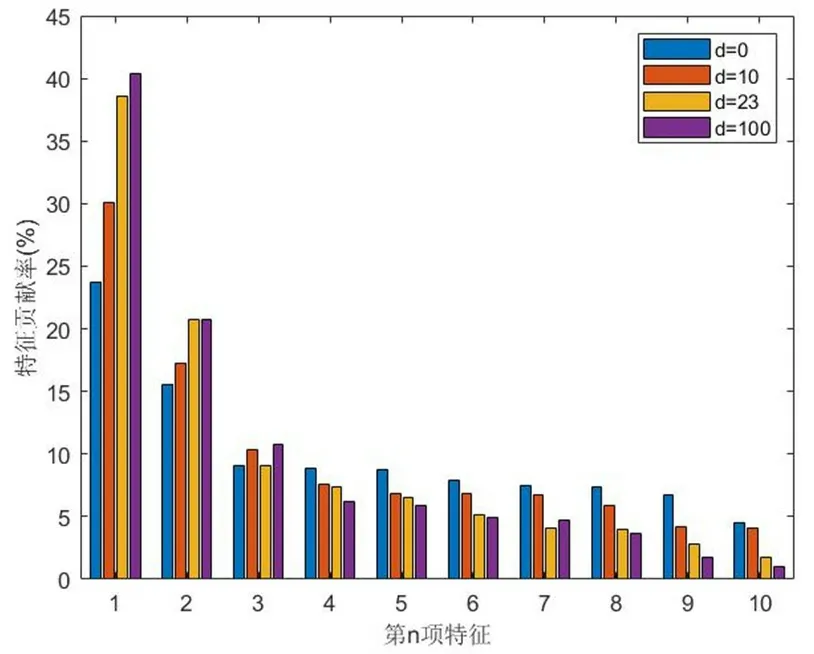
图5 不同时延下前十维的特征贡献比例
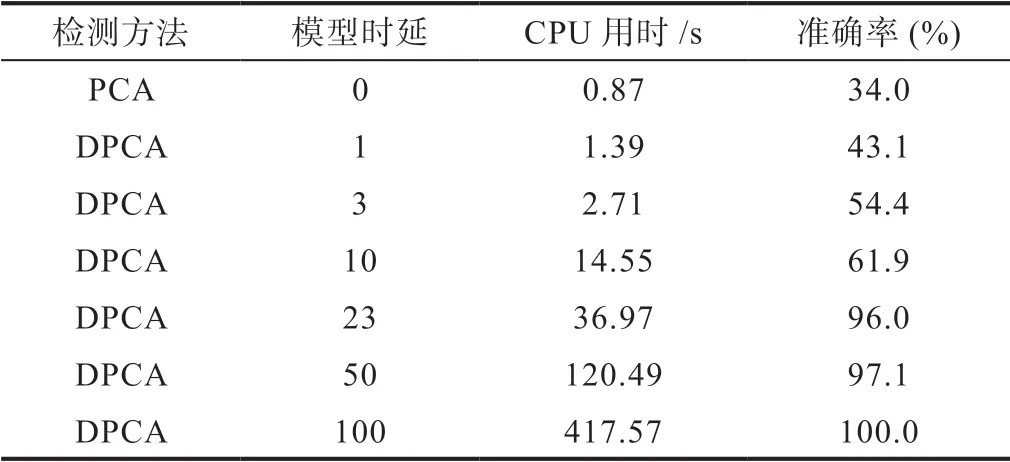
表1 不同模型下的检测准确率和程序运行时间
3 结论
(1)DPCA方法适用于从冗余的船舶主机控制系统传感器数据中提取有用的数据特征,识别异常数据,并据此排查出传感器的偶发性故障。
(2)和传统的PCA方法相比,由于DPCA考虑了多源数据之间时延关系,能够更好地完成数据对齐和特征提取的工作,而PCA方法更容易受到噪声和时延影响,难以反映数据的真实信息。
(3)实例分析表明,基于DPCA的冗余传感器数据处理方法,为船舶主机控制系统传感器偶发性故障检测提供了新思路,当延时达到与客观最大延时相近时,检测准确度高,具有较为广阔的应用场景。
