基于SLIC和马氏距离混合核函数聚类的脑肿瘤图像分割算法

王志刚，冯云超，黄 灌

(湖南师范大学 信息科学与工程学院，长沙 410081)

近年来，脑肿瘤的发病率和死亡率正在逐年攀升，且患者多为恶性肿瘤，它对人类的生命健康造成了严重的危害[1].利用计算机技术准确获得脑肿瘤的尺寸和位置等信息，能够帮助医生作出准确的诊断[2]，同时，在手术定位、创建病情档案、建立肿瘤模型等方面也有重要作用[3].因此，将脑肿瘤图像从MRI 影像中准确地分割出来对脑部疾病的诊断具有重要的意义.

在临床中，通常由医生手动绘制脑肿瘤边界，这不仅需要医生掌握较多的专业知识，还会耗费大量的时间和精力，且分割结果易受主观因素的影响，可能会因医生水平的不同而出现明显的差异.因此，实现脑肿瘤图像的自动分割，一直是学者们研究的热点问题.

模糊C均值聚类(fuzzy c-means, FCM)算法是一种经典的图像分割算法，也是一种无监督的聚类分析方法，已被广泛应用于医学图像分割领域[4].但是，该算法对噪声较为敏感，且初始聚类中心随机确定，容易陷入局部极值，当不同类别样本特征差异较小时，聚类精度较差.为此，学者们进行了大量的研究和改进，祖志文等[5]使用粒子群算法初始化聚类中心，提高了算法的稳定性；Yang 等[6]提出一种基于核函数及空间邻域信息的模糊聚类算法，扩大了不同样本间的特征差异，提高了算法的抗噪性；王燕等[7]将核函数与马氏距离相结合，提出了KM-FCM 算法，增强了算法的噪声鲁棒性.

针对传统模糊C 均值聚类算法对噪声敏感，初始聚类中心不确定，聚类精度不高以及无法对脑肿瘤MRI 图像准确分割的问题，本文将马氏距离混合高斯核函数引入到模糊C 均值聚类算法中，结合SLIC 算法和粒子群算法，提出一种新的脑肿瘤图像分割方法，研究其分割精度和有效性.

1 各向异性滤波

传统消噪方法虽然能较好地去除噪声，但却损害了原信号的强度，模糊了图像的边缘，不能很好地满足医学图像分割的需要.因此，本文采用各向异性滤波进行图像的预处理，在去除噪声的同时还可以把图像的边缘较好地保留下来.

各向异性滤波是把图像看成物理学的力场或热流场，图像像素总是朝着跟其值差异不大的地方流动，那些差异大的地方(边缘)得以保留.因此，各向异性滤波本质上是图像边缘保留滤波器(EPF)[8]，其在各方向上的扩散可表示为

2 算法描述

2.1 线性迭代聚类预分割

为避免残留噪声和散点对图像分割造成干扰，

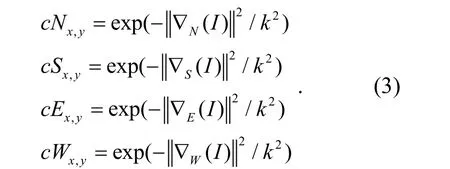
本文首先采用SLIC 算法对图像进行预分割.简单线性迭代聚类(simple linear iterative clustering,SLIC)算法是Achanta 等[9]提出的一种新的聚类算法，它能够生成大量形状规则、相对均匀的超像素块，可以有效避免过分割和欠分割现象.SLIC算法的具体步骤[10]如下：

1)初始化种子点.假设图像有N个像素点，首先，将其分为K个超像素块，则超像素块尺寸约为N K，超像素块间的距离可用S=N K来表示；其次，计算出所有像素点的梯度值，为避免影响后续的聚类结果，让种子点在邻域3×3 的窗口内移动，并且保证其移动到梯度值最小的位置上，以防止种子点被分配到影像的边缘位置或噪声点的位置；最后，分配对应标签到每个种子点上.

2)相似性度量.对每个像素点进行搜索，计算出像素点与种子点之间的相似程度(包括颜色距离和空间距离)，不断迭代直到算法收敛.其距离关系为

2.2 粒子群算法确定聚类中心

粒子群优化(particle swarm optimization, PSO)算法是由Kennedy 和Eber-hart 提出的群智能优化算法[11].其具体流程如下：

其中，wmax表示w的最大值，通常取0.9；wmin表示w的最小值，通常取0.4；t表示当前的迭代次数；tmax表示最大迭代次数.

2.3 基于马氏距离混合核函数的聚类算法

2.3.1 混合核函数聚类

由于单一高斯核函数只有唯一的可调参数σ，所以其具有很强的局部性，导致聚类算法的学习和泛化能力不强[12].本文采用混合高斯核函数替代单一高斯核函数，这样就可以通过调整多个σ参数来优化样本数据在核空间中的分布，从而提高核模糊聚类算法的性能.混合高斯核函数的定义为

2.3.2 马氏距离混合核函数聚类

传统高斯核函数虽具有很强的适应性，但其对数据差异性的度量方式是欧氏距离，而欧氏距离并没有考虑特征之间可能存在的耦合关系，因此它不能有效地描述2 个样本点之间的全局性关系，往往不能取得令人满意的效果.

马氏距离是由印度统计学家Mahalanobis 提出的[13]，因其引入了协方差矩阵，所以可以更好地描述2 个样本点之间的全局性关系，其定义为

2.4 算法步骤

本文所提算法的具体实现步骤如下：

1)使用各向异性滤波对图像进行预处理，设定迭代次数t= 20，导热系数k= 15，平滑系数λ= 0.15.

2)用简单线性迭代聚类算法对预处理后的图像进行分割，超像素块大小设为15 个像素.

3)设定粒子群算法的相关参数，即粒子群规模N= 30，最大迭代次数tmax= 30和学习因子c1=c2= 2，并求得初始聚类中心v0.

4)设定聚类数目c= 3，迭代终止条件ε= 10-5，最大迭代次数Tmax=100，高斯核数目g= 2，高斯核参数σ1=150，σ2= 20，约束系数λ=0.6.

5)输入由步骤3)获得的初始聚类中心v0，再根据式(17)～式(18)，不断更新聚类中心vi和隶属度矩阵U.如果J(i) -J(i- 1)≤ε或者达到最大迭代次数，则停止迭代；若不满足上述条件，则继续执行本步骤.

6)迭代停止后，根据最终得到的隶属度矩阵把目标像素指定为相应的最佳聚类中心的值，并输出图像.

7)结合形态学对图像进行后处理，即平滑脑肿瘤图像的边缘.

3 实验结果及分析

3.1 实验环境

本次实验的脑肿瘤MRI 图像来自BraTS2018数据库，该数据库的MRI 图像提供了4 种图像序列，分别是T1，T1c，T2 和FLAIR.由于FLAIR图像序列在成像过程中水分子信号被抑制，故常被用于肿瘤诊断[14]，本文亦选择该图像序列.实验环境为Windows10、AMD Ryzen 5 3500U 处理器、16 GB 内存，以及Matlab 2018a.

3.2 抗噪实验

由于MRI 图像在成像过程中经常受到高斯噪声的干扰，所以在图像中分别添加方差为0.005，0.01，0.02 和0.03 的高斯噪声，并用本文所提算法对MRI 图像进行分割，结果如表1 所示.

表1 不同强度噪声下的分割结果

由表1 可知，当噪声方差为0.005～0.02 时，分割结果相对稳定，能较好地将脑肿瘤图像分割出来，这说明算法具有良好的抗噪性；当噪声方差为0.03 时，消噪后的图像开始变得模糊，脑肿瘤图像的边缘部分开始出现误分割的现象.

3.3 脑肿瘤分割实验

为了验证所提算法分割脑肿瘤图像的有效性，从BraTS2018 数据库中随机挑选某位患者的脑肿瘤MRI 图像，抽取3 个层面进行图像分割，并且分别与FCM 算法[15]和KFCM 算法[16]的分割效果进行对比，结果如图1～图3 所示.

从图1～图3 可看出，在FCM 和KFCM 算法的分割结果中，脑肿瘤图像的边缘部分出现了一定程度的误分割现象，且有一定的散点存在；本文算法则能较好地处理脑肿瘤图像细节，且分割后无明显散点，其分割效果最接近于真值图像.

图1 切片1 分割效果对比

图3 切片3 分割效果对比

图2 切片2 分割效果对比

为了避免主观评价因素的影响，本文选择Dice，Jaccard，Sensitivity和Accuracy共4 个评价指标对算法分割精度进行评估，其定义分别为

其中，TP为正确分割的目标区域；FP为误分割的目标区域；FN为没有检测到的目标区域；TN为一定的非目标区域.

仍以上述3 幅脑肿瘤MRI 图像为例，将本文算法与FCM 算法和KFCM 算法的4 项评价指标进行比较，结果如表2 所示.

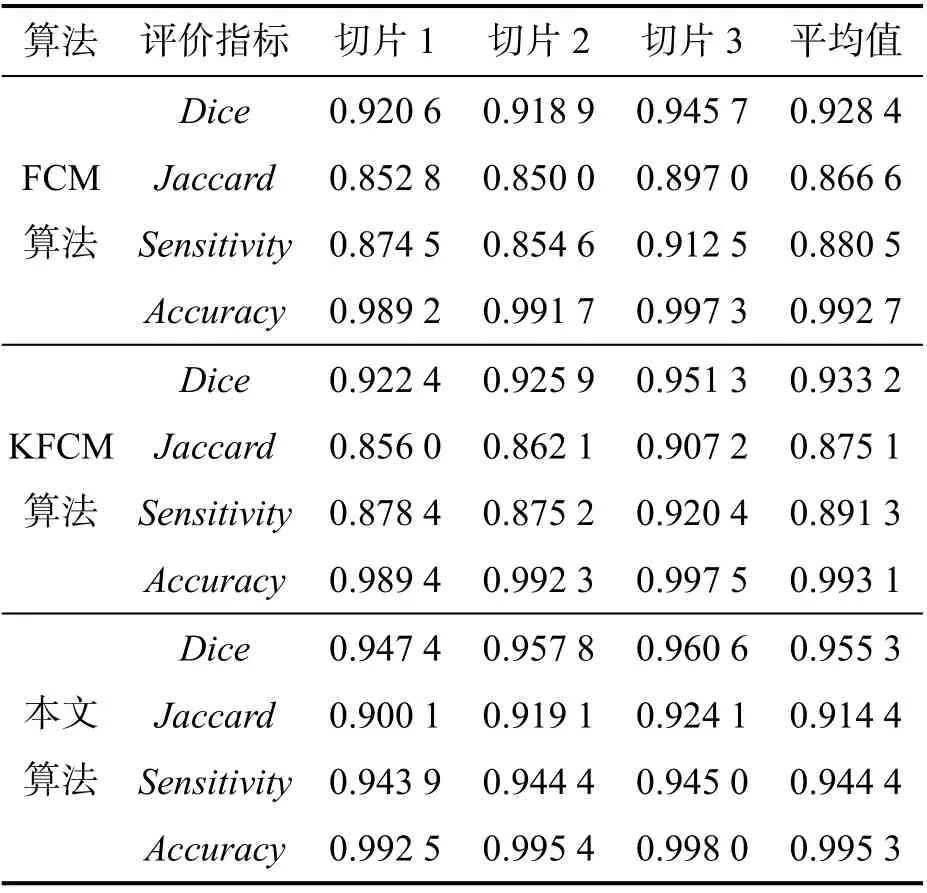
表2 本文算法与其他算法的分割性能对比

由表2 可以看出，本文算法相较传统聚类算法在各指标上均有一定提升：Dice平均值相较传统算法高出2.21%～2.69%；Jaccard平均值相较传统算法高出3.97%～4.78%；Sensitivity平均值相较传统算法高出5.31%～6.39%；Accuracy平均值相较传统算法高出0.22%～0.26%.在脑肿瘤图像分割中，通常以Dice和Jaccard作为主要指标，其值越接近1，代表分割效果越好.本文所提算法从实验中得出的Dice平均值和Jaccard平均值均较高.

4 结束语

本文所提脑肿瘤图像分割方法，利用各向异性滤波进行图像预处理，具有良好的抗噪性；通过粒子群算法确定初始聚类中心，提高了算法的稳定性；利用多个马氏距离高斯核函数进行数据映射，可以优化算法的分割性能.实验结果表明，与FCM 算法和KFCM 算法相比，所提算法具有较好的噪声鲁棒性，其分割精度更高，能将脑肿瘤图像从脑MRI 影像中准确地分割出来，是一种有效的脑肿瘤图像分割算法.但本算法也存在一定缺陷，如高斯核的各参数和权重不能自动调节，需要人为干预，这将是下一步研究的重点.