一类耦合系统的解及共振

魏其萍，王 跃

(1. 贵州民族大学 数据科学与信息工程学院，贵阳 550025；2. 贵州大学 数学与统计学院，贵阳 550025)

研究Kirchhoff 型方程所构成的耦合系统

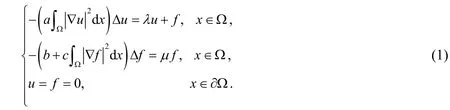
受上述文献启发，本文以特征值问题为铺垫，结合代数分析方法，考虑耦合系统(1)解的存在性，得出其共振经典解，并用实例证明该结论的可靠性，所用方法和结论与文献[13]均不同.

1 主要结果及证明

(iv)当f(x) ≡0 时，对任意λ＞0 ，系统(1)均有无穷多解.

因为可以将系统(1)中第2 个方程的解作为第1 个方程的耦合函数，在此情形下，可将第2 个方程的解在第1 个方程中的作用理解为一种函数扰动，所以系统(1)被称为弱耦合系统.基于弱耦合性，第一步便是要获得第2 个方程的解，为此，首先考虑系统(1)的第2 个方程，即

再将方程(4)的解代入系统(1)的第1 个方程，即

2 实例与结论

3 结束语