基于小波包能量和层次熵的D-S 证据理论的轴承故障诊断技术

叶小芬，王起梁，祝 敏，张浩瀚

（中车戚墅堰机车车辆工艺研究所有限公司，江苏 常州 213011）

0 引言

滚动轴承是列车齿轮传动系统的关键部件，滚动轴承的故障诊断一直受到人们的重视。近几年，国内外学者对轴承振动信号的分析开展了大量研究，常用的基于时频域的故障特征提取方法有短时傅里叶变换、局部特征尺度分解、局域均值分解、经验模态分解[1]、小波及小波包[2-3]分析、Hilbert-Huang 变换[4]/谱峭度分析[5]等。小波包变换被证实为非常有效可行的特征提取方法，另外分形维数、近似熵和样本熵等非线性方法的引入极大地丰富了故障诊断的方法和技术；此外，DS 证据理论给出了多源信息的组合规则，广泛应用于信息融合、决策分析等领域[6]。

本研究利用小波包对轴承振动信号多层分解，构造小波包能量分布和层次熵为故障特征集，分别建立BP 神经网络实现轴承故障分类诊断，最后应用D-S 信息融合理论，将2 种方法的诊断结果融合，以提高轴承故障诊断的准确率。故障诊断技术原理如图1 所示。

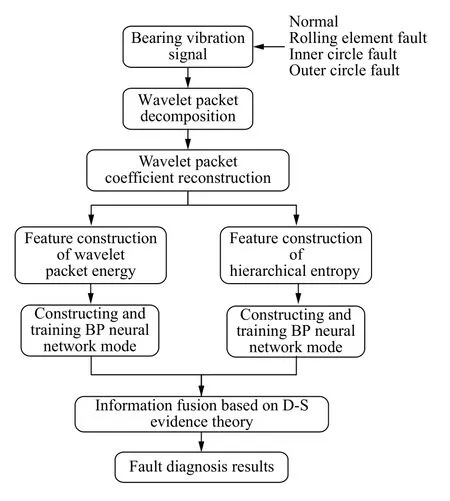
图1 轴承故障诊断技术原理图Fig.1 Schematic diagram of fault diagnosis technology of bearing

1 算法原理

1.1 小波包分解

小波包是小波分析理论的重要组成部分，小波包与小波的主要区别在于小波包每一层分解都同时分解低频的近似信号和高频的细节信号，在保留了信号完整性的基础上又提升了信号的低、高频段分辨率，一个3 层分解的小波包树形结构见图2，分解后得到的数据称为小波包（或称频带）。

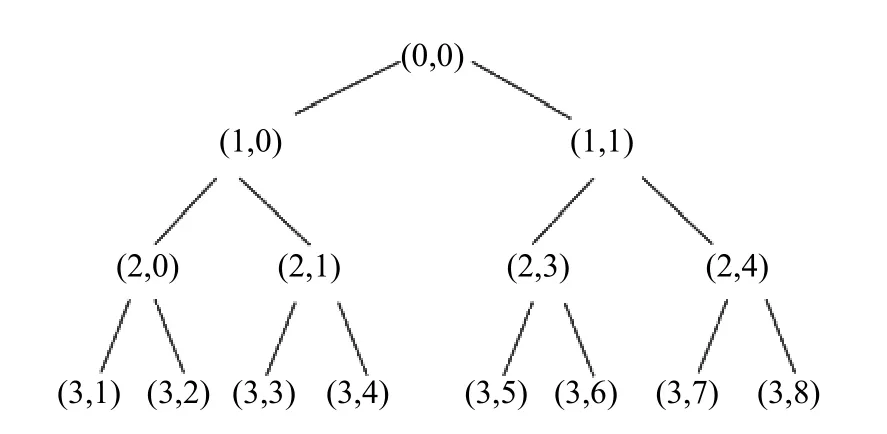
图2 小波包树形结构图Fig.2 Tree structure diagram of wavelet packet

不同故障模式的振动信号小波包能量值分布呈现不同的变化趋势，因此，构造小波包频段能量分布作为故障特征集[7]，进行轴承的故障诊断。

构造步骤如下[8]：

1）N层小波包分解：如进行3 层分解，Matlab语句为L=wpdec(signal,3,'db4')，可以提取第3 层从低频到高频23=8 个频带成分的小波包分解系数。

2）小波包分解系数重构：Matlab 语句W3i=wpcoef (L,[3,i])对第3 层小波包分解系数进行重构，提取各频带信号。用S3i(i=0,1,···,7)表示第3 层小波包分解系数的单支重构信号。

3）计算各频带信号的能量，构造能量特征向量。设W3i对应的频带能量为E3i，则：

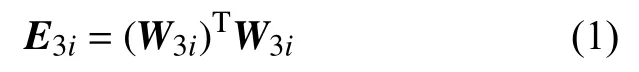
4）小波包能量归一化处理，能量特征向量E′为：

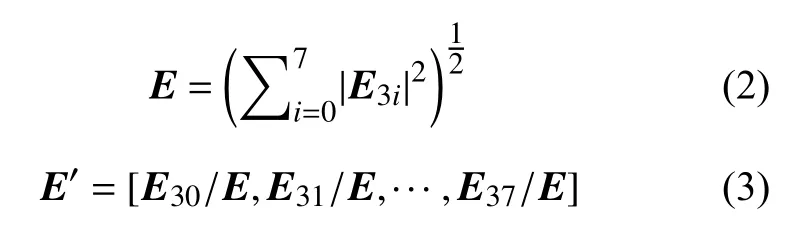
1.2 小波熵包层次

熵是时间序列复杂度的一种表征参数[9]，广泛应用于故障诊断领域，不同故障模式的振动信息的复杂程度的不同，则其熵值也不一样，因此可以构造以熵为故障特征集进行故障诊断研究，计算过程如下：

1）同1.1 中的第1 个步骤，对轴承振动信号进行小波包3 层分解；分别计算23=8 个节点信号的样本熵。

2）以各节点的样本熵（即层次熵）HierEntropy作为故障特征向量为：

样本熵的计算过程[10]如下：

①对于一个n点 时间序列x(1),x(2),···,x(n)，造一个m维向量：

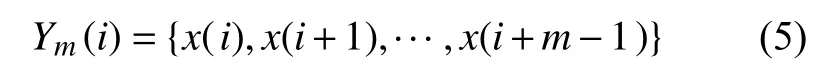
其中，1≤i≤n-m+1。

②计算Ym(i)和Ym(j)之间距离：

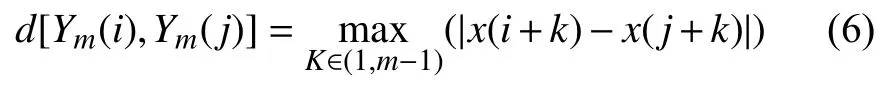
③设置容限ɛ，统计每个Xm(i)满足d[Ym(i),Ym(j)]≤ε的数目，记为Ii。

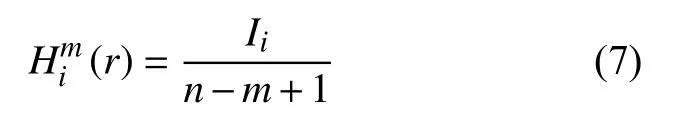
⑤用相同方法求出Hm+1(r)。

则该时间序列的理论上的样本熵定义为：

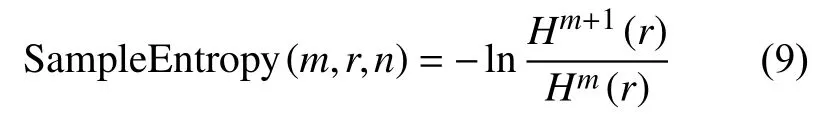
1.3 D-S 证据理论[11]

首先，定义mass 函数：在识别框架 Θ下，如果映射m：2Θ→[0,1]满足

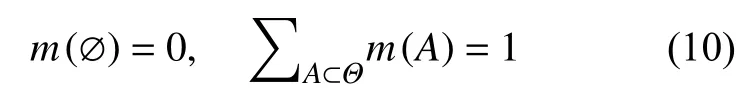
则称其为定义在 Θ上的mass 函数。集函数m(A)即对子集A本身赋予的置信度，在本研究中，A表示每一种可能出现的故障模式的概率，而识别框架就是所有故障模式的并集。

然后，定义置信函数：如果映射Bel:2Θ→[0,1]满足：

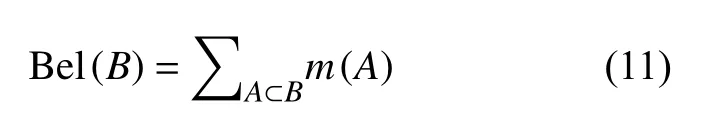
则称其为定义在 Θ上置信函数。集函数Bel(A)表示对子集A及其全部子集赋予了置信度。Bel(A)为A的所有子集可能性度量之和，表示了对A的信任。

D-S 证据理论的组合规则解决了已知n个相互独立的基本概率赋值，确定组合之后的基本概率赋值的大小。

假设，Bel1，Bel2是同一个识别框架下的2 个信任函数，m1,m2分别为其对应的基本概率赋值，那么m=m1⊕m2为[12]：

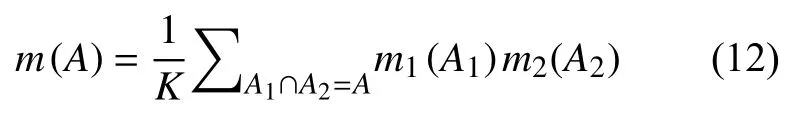
其中：符号 ⊕表示Dempster 组合规则；K为规范化因子，由下式定义：

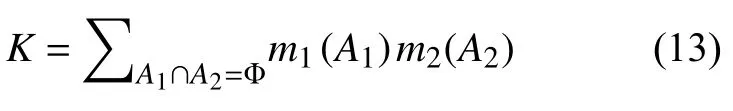
若m(A1)=max{m(Ai),Ai⊂Θ}，则A1为判决结果。

2 数据处理与分析验证

本研究采用的轴承数据来自于美国凯斯西储大学（Case western reserve university，CWRU）轴承数据中心，采样轴承型号为SKF-6205，电机转速分别为1730、1750、1772、1797 r/min，采样频率为12 kHz。

2.1 基于小波包能量的故障诊断

1）小波包能量特征提取与分析。

对轴承振动数据进行预处理，按照1.1 节步骤构造小波包频带能量特征，选取各组轴承状态的一组数据进行能量分布图绘制，结果如图3 所示。

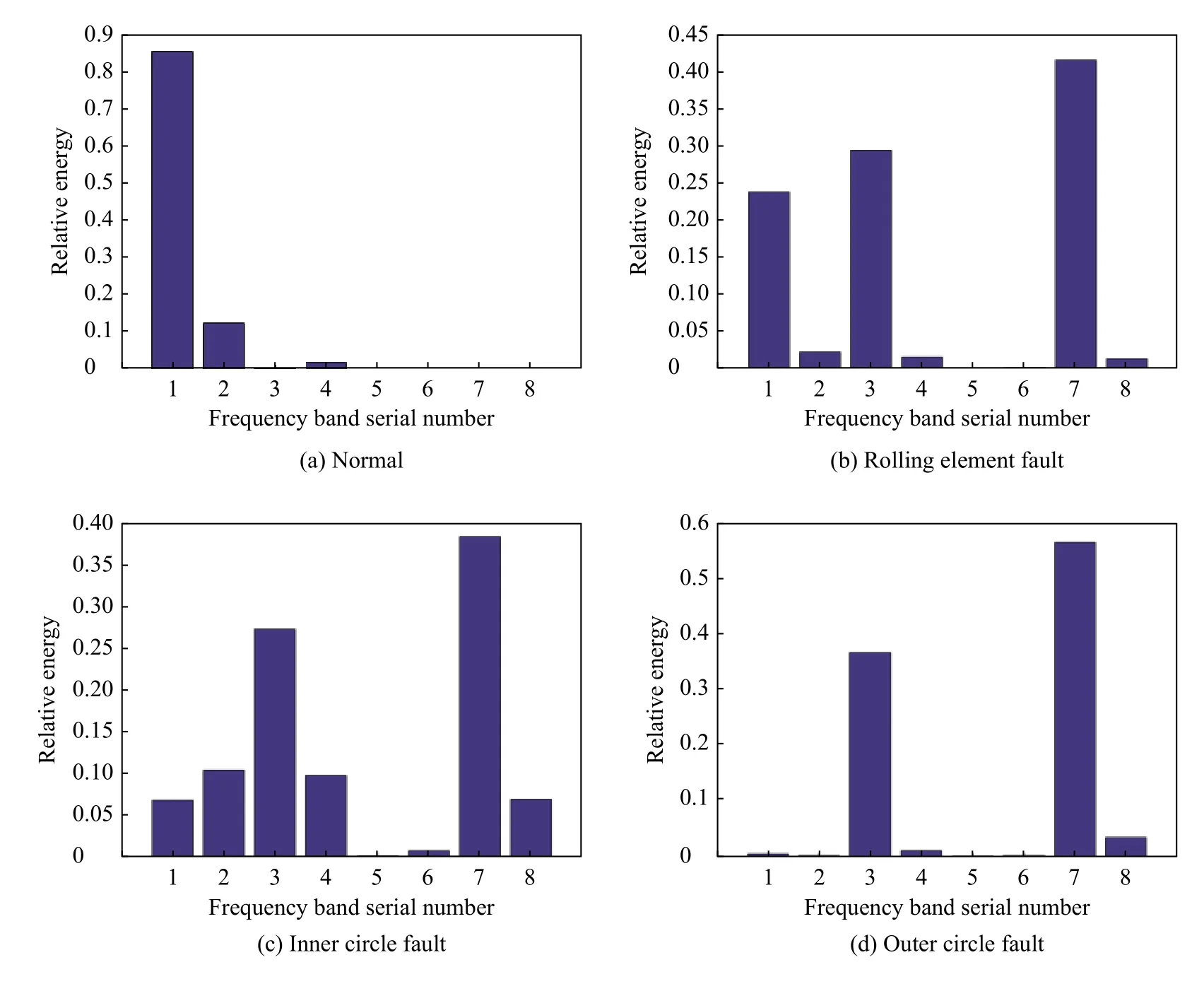
图3 轴承4 种状态的小波包能量频带分布图Fig.3 Distribution graph of energy-frequency band of wavelet packet under four kinds of bearing status

从故障特征能量分布可以看出：正常状态和故障状态的小波包能量分布存在明显差异，正常轴承的能量值较大的在1、2 频段，其他频道能量几乎很少，而故障状态在其他频段存在较大能量；3 种故障类型的轴承特征向量值分布和各频道能量大小也存在差别。因此，将小波包能量分布作为BP 神经网络的输入，通过BP 神经网络训练实现轴承故障分类诊断。

2）BP 神经网络的建立与训练。

BP 神经网络本质是反向传播算法，采用均方误差作为代价函数，如式（14），即每输入一个样本，便将网络的实际输出与期望输出做比较，算法将调整网络参数以使得均方误差最小。

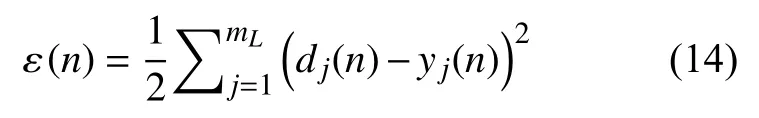
其中，dj(n)为期望的输出，yj(n)为n时刻神经元j的输出。

BP 神经网络构建步骤如下：

①确定神经网络输入：以1.1 节中式（3）获取的能量特征向量作为输入样本E′。

②设置神经网络输出：采用4 个二进制元素的向量表示，其中（0,0,0,1）为外圈故障，（0,0,1,0）为内圈故障，（0,1,0,0）为滚动体故障，（1,0,0,0）为正常。

③创建神经网络、设置训练参数：net=newff(minmax(Train),[18,4],{'tansig','purelin'},'traing dm')，输入层、隐含层和输出层的节点个数分别为8、18、4；训练精度要求为0.01，学习率0.15。

④BP 神经网络训练：net=train(net,Train,T)，训练结束后检查训练结果是否符合精度要求。如果符合要求则输入测试样本，测试网络性能；否则，重新网络训练，直至满足精度要求。

⑤应用训练好的神经网络进行仿真预测，[Y,pf,Af,perf]=sim(net,P,Pi,Ai)。本研究统计集和测试集的诊断如图4 所示，图中纵坐标代表类别标签，其中，1 代表（1,0,0,0），2 代表（0,1,0,0），3 代表（0,0,1,0），4 代表（0,0,0,1）。

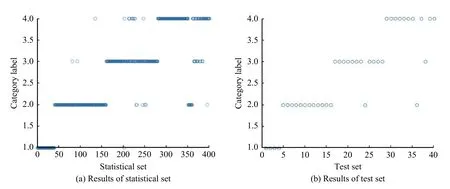
图4 诊断分类结果Fig.4 Results of diagnosis classification

2.2 基于层次熵的轴承故障诊断

对轴承振动数据进行预处理，按照1.2 节中方法，对同一故障尺寸0.177 8 mm（7 mils）的4 种轴承状态下的样本熵进行计算，结果见表1。由表1可见：轴承不同状态下其样本熵是不同的，同一状态的样本熵差别不大；滚动体故障的样本熵大于内圈故障，内圈故障样本熵又高于外圈故障，主要是由于外圈固定在轴承座上的，外圈信号传递路径较短，干扰小，故样本熵较小；而内圈和滚动体随轴转动，故障机理更复杂，因此熵值较大，但两者样本熵比较相近，不易区分，因此需要提取层次熵来进行进一步比较。

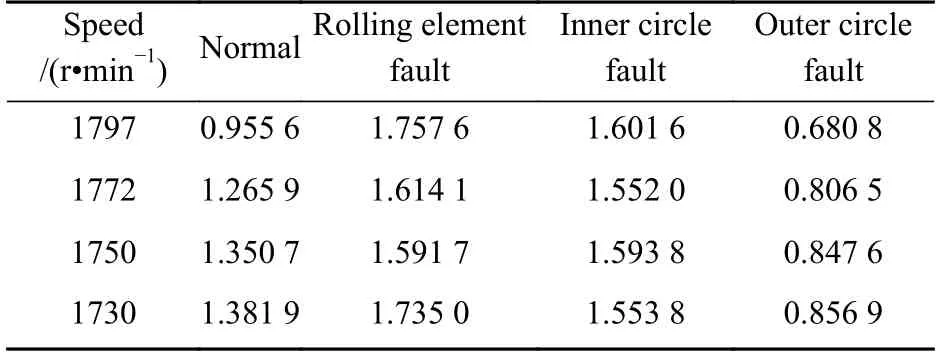
表1 轴承4 种状态下的样本熵Table 1 Sample entropy in four kinds of bearing status

4 种状态轴承振动信号的层次熵分布情况见图5。可见，3 种故障状态的高频部分熵值较高，这也说明故障振动信号的高频和低频部分都隐藏有故障信息；正常状态的层次熵从低频到高频逐渐下降，说明正常状态下轴承振动信息主要包含在低频部分。以层次熵构造故障特征向量HierEntopy 作为BP 神经网络的输入进行分类诊断。

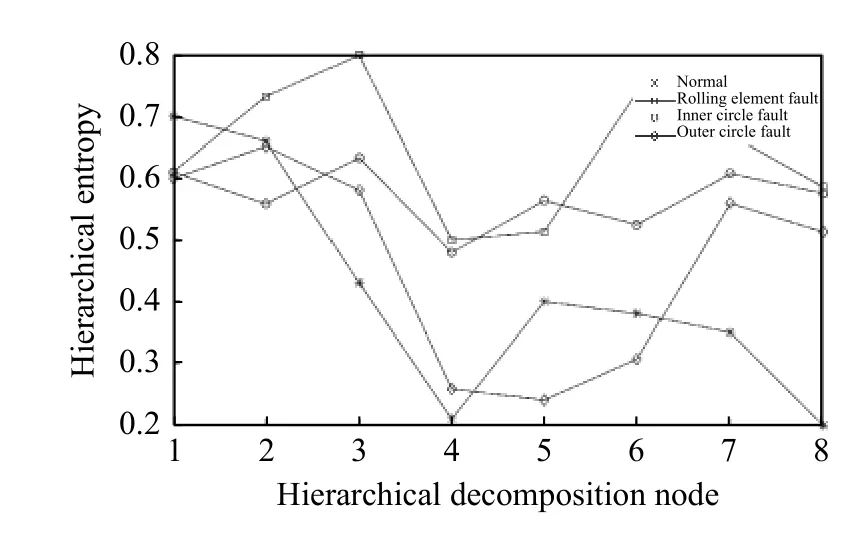
图5 4 种轴承状态下的层次熵Fig.5 Hierarchical entropy in four kinds of bearing status

2.3 D-S 证据理论信息融合

将基于小波包能量和层次熵的诊断结果统计准确率统计后，建立如下混淆矩阵CM（Confusion Matrix）[13]：

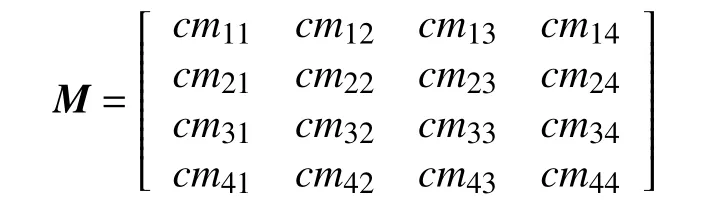
cmi j第i类故障状态样本被诊断为第j类故障状态的样本数与真实第i类故障状态的测试样本总数的比值；当i=j时，即对角线元素为各故障状态能够被神经网络正确分类的百分比。因此，可以应用混淆矩阵来表征反映神经网络对故障的分类能力。

神经网络识别出第j种故障状态的局部可信度为：

全局可信度为：

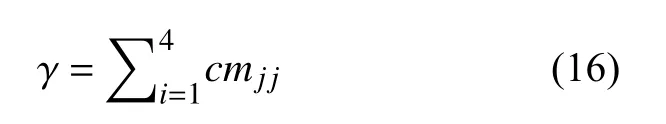
对于某一次神经网络的输出结果pj，基本概率赋值为：

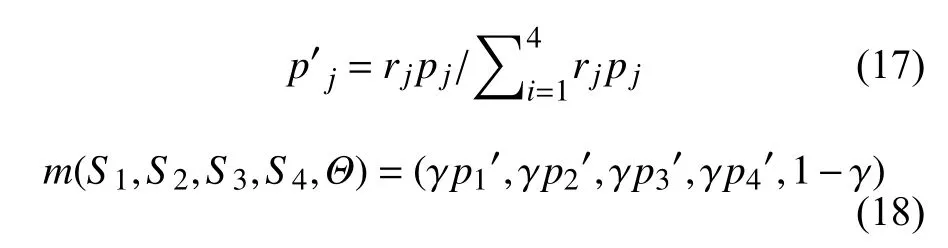
其中，识别框架为Θ=(S1,S2,S3,S4,Θ)，S j为轴承第j种状态。

2 种方法的诊断可信度见表2。根据式（18）选取某一条数据（滚动体故障）的2 种方法的基本概率分配函数赋值见表3。结合D-S 证据合成规则式（12），经过D-S 证据融合，诊断为基本概率从0.743 8、0.789 2 提升到0.980 0（表4）。

表2 诊断可信度Table 2 Diagnostic credibility

表3 基本概率赋值Table 3 Basic probability assignment of diagnosis

表4 D-S 证据融合诊断的基本概率赋值Table 4 Basic probability assignment of fusion diagnosis based on D-S evidence theory

3 轴承故障诊断软件系统的实现

将上述诊断技术方法可视化，开发相应的故障诊断软件，软件包括常见时域分析、频域分析、小波包分析、BP 神经网络等功能界面，并具有数据载入、分解结果保存、数据导出、图片保存等功能。主要功能界面如图6 所示。

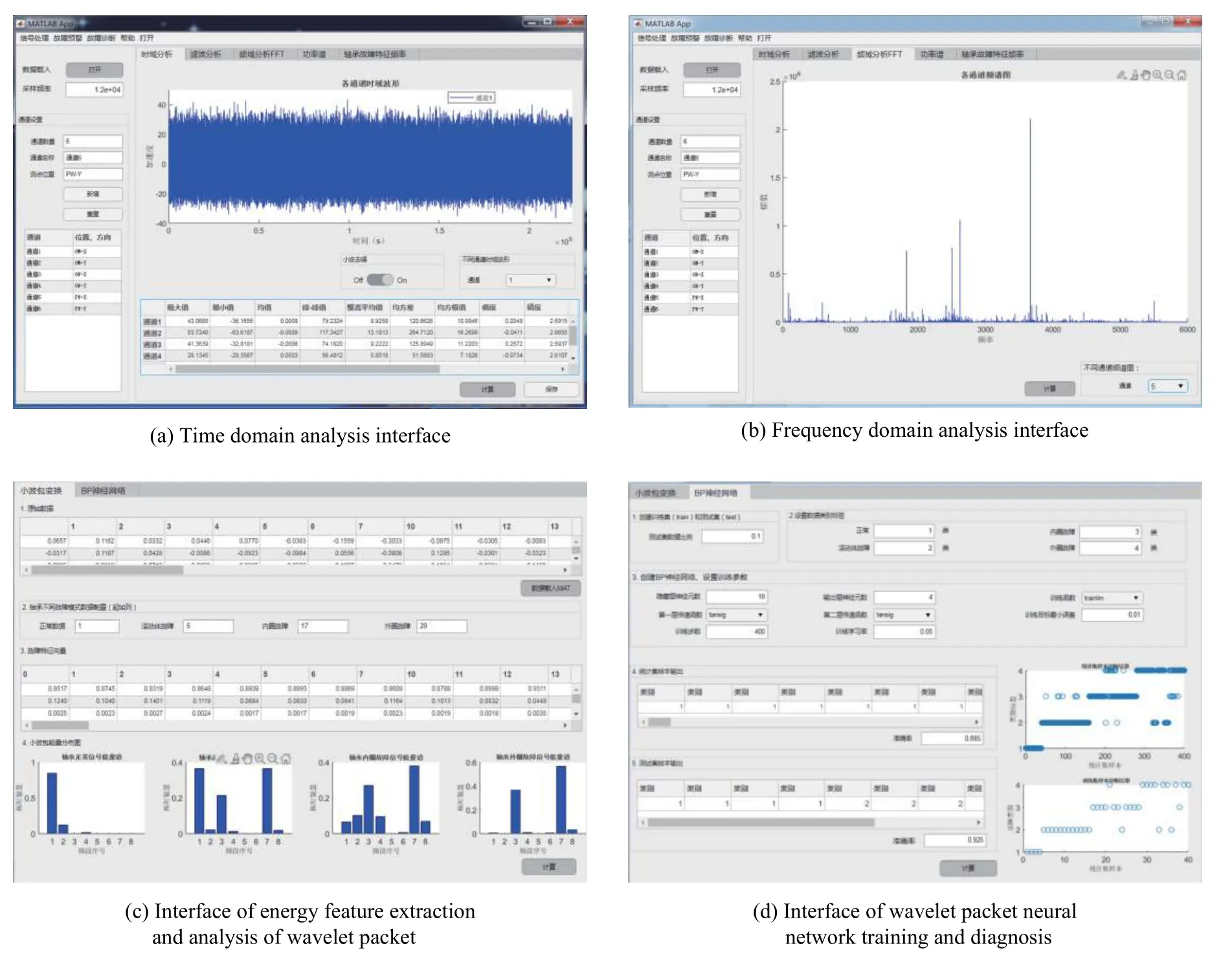
图6 功能界面Fig.6 Function interface

4 结论

1）利用小波包对轴承振动信号多层分解，构造小波包能量分布故障特征集，建立BP 神经网络实现轴承故障分类诊断。

2）采用基于层次熵和BP 神经网络构建了轴承故障诊断模型，实现轴承不同故障模式的分类诊断。

3）应用D-S 信息融合理论，实现2 种诊断结果的信息融合，对比单一方法诊断，准确度分别提升了6%和4%，表明D-S 证据理论相结合方法用于复杂机械的故障诊断是可行和有效的。

4）该研究方法为各类轴承故障的诊断提供一种高效可行的思路；同时开发故障诊断软件，具有一定的实用性价值。