隔墩对双向流道泵装置内流及压力脉动影响研究

赵振江，石 磊，蒋红樱，成 立，张 帝，卜 舸

（1.泗洪县水利局，江苏宿迁223900；2.江苏省水利工程科技咨询股份有限公司，南京210029；3.扬州大学水利科学与工程学院，江苏扬州225009；4.江苏省水利勘测设计研究院有限公司，江苏扬州225009）

0 引 言

在沿江滨湖地区，针对灌溉排水结合的双向抽水需求，建设了众多双向抽水泵站，双向流道泵站通过调节双向流道进出口闸门实现双向引水排水，得到广泛应用［1，2］，众多学者对泵装置的各项性能展开研究［3-5］。

刘超等［6，7］提出新型曲线扩散出水结构和进水导流墩设计方案，消除双向流道泵装置进水流道内的涡带；成立等［8，9］通过RNG 湍流模型对双向流道内水流流态进行模拟，揭示了双向流道内部流动规律，阐述了采取消涡措施的必要性；Zhu等［10］建立了双向流道泵装置模型试验台，观察分析了流道内水流特性并通过试验对各种方案进行比较，给出了可以有效改善流态的措施；泵装置内部压力脉动是诱导水力激振的主要原因，近年来学者展开大量压力脉动及振动的研究［11-14］。姚丹等［15］针对灯泡贯流式机组压力脉动特性展开研究，发现动静干涉是引起机组压力脉动的最主要原因；张德胜等［16］对轴流泵水力模型不同工况压力脉动特性展开研究，揭示了轴流泵内部不同位置处压力脉动及振动规律；杨帆等［17，18］研究了轴流泵装置不同叶片安放角下各工况压力脉动变化规律，并通过水听器试验分析了流道的内流脉动与流动噪声的时频特性；Duan等［19］对箱涵式轴流泵装置内部压力脉动与振动位移进行测量，发现叶轮进口压力脉动是水力诱发振动的主要原因。

为进一步探究双向流道内流及脉动特性，本文在泵装置进出水流道中加入隔墩，在不同工况进行数值模拟与分析，对加入隔墩后特征位置压力脉动及流态影响作出研究。

1 泵装置数值计算模型及方法

1.1 泵装置计算模型

本文以某双向流道泵站为计算模型，采用“X”型双层箱涵式进出水流道，其主要功能是汛期向外河排涝，平时向内河引水用于改善城区水环境，因此需双向引排。选用4 台立式轴流泵机组，配500 kW 立式异步电机4 台套，主水泵叶轮直径D=1 600 mm，转速n=245 r/min，单机设计流量Qd=7.3 m3/s，叶片数Z=3，导叶叶片数Zd=7。在设计排涝工况下，内河侧水位为14.0 m，外河侧水位为16.9 m。泵站计算模型包括进出水流道延伸段、进出水流道、叶轮及导叶，对进出水流道内部设置厚400 mm的隔墩，计算模型如图1。

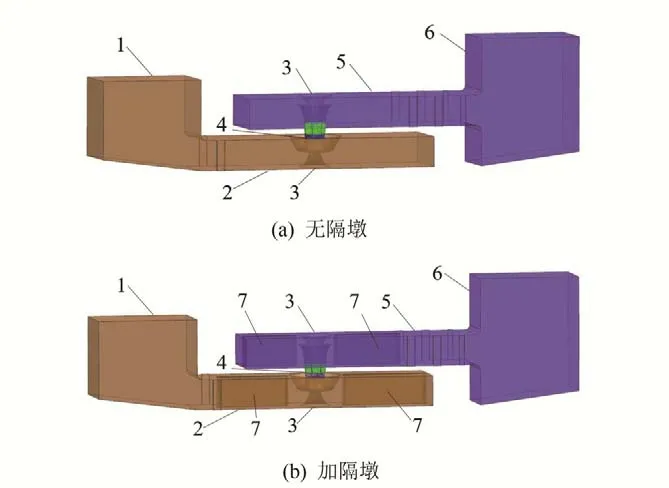
图1 双向流道泵装置三维模型Fig.1 Three dimensional model of two-way reversible pumping system

1.2 数值计算方法及网格划分

为研究双向流道泵装置内部流态及压力脉动特性，基于连续性方程与Navier-Stokes 方程（N-S 方程），通过采用ANSYS CFX 软件进行数值模拟。其中定常与非定常计算均采用RNGk-ε模型，根据南水北调泵站流道计算经验，该模型可以满足工程数值模拟需求。

对叶轮、导叶、进、出水流道及其延伸段分别采用ANSYS TurboGrid 与mesh软件进行网格划分，网格示意图如图2。为确保数值模拟准确性，在设计流量工况对泵装置不同网格数进行数值计算，经过网格无关性分析确定当泵装置整体网格数达到756 万格时，装置扬程变化微小，网格数对计算结果影响较小，确定最终整体计算网格数为756万。

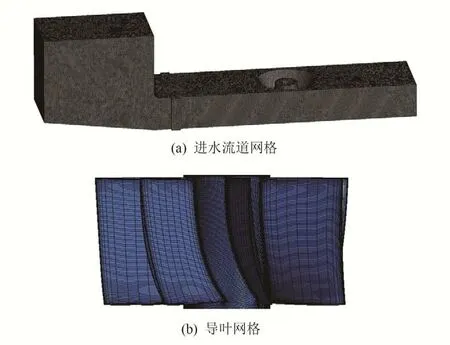
图2 网格划分示意图Fig.2 Grid division diagram

1.3 边界条件及计算设置

计算区域包括叶轮、导叶、进、出水流道及延伸段。计算域进口采用质量流进口边界条件，出口采用压力出口边界条件，设置为1 个标准大气压，进出口的自由水面采用钢盖假定设置为对称面；叶轮直径为1 600 mm，将叶轮设置为旋转域，转速为245 r/min，其余部分设置为静止域；壁面采用无滑移边界条件，近壁区域采用标准壁面函数处理。

在定常计算结果收敛的基础上对双向流道泵装置进行非定常数值计算，叶轮与进水流道及导叶间交界面选用Transient Rotor Stator；设置计算总时长为1.469 387 755 s，即6 个叶轮旋转周期，时间步长选取为叶轮旋转6°所需时长，即0.004 08 s。

1.4 数值计算有效性验证

为证明上述双向流道泵装置数值模拟准确性，在江苏省水利动力工程重点实验室的高精度水力机械试验台进行了双向流道泵装置模型试验，水力模型试验采用叶轮模型直径为300 mm，水泵装置模型比尺为1∶5.33，与原型根据等扬程进行换算，确定模型泵试验转速为1 307 r/min，如图3 所示。将试验结果换算至原型泵装置性能数据，与数值模拟不同工况结果进行外特性对比，如图4，对比结果表明，试验与数值模拟得到的性能曲线整体趋势相似，在设计工况下吻合度较高，试验与数模整体拟合性较好，数值模拟采用的计算方法及结果有效。

图3 模型试验装置图Fig.3 Model test device diagram

2 计算结果分析

2.1 隔墩对双向流道流态影响分析

为探究隔墩对双向流道内部流态影响，在有无隔墩不同工况下进行数值模拟计算：小流量工况0.8Qd、设计流量工况1.0Qd、大流量工况1.2Qd。

分别在距进、出水流道底板与顶板0.4 m 处设置水平截面，图5为各工况下进、出水流道所选取截面的速度云图与流线图。由图5可知，在各工况进、出水流道盲端均存在水流低速区。当不布置隔墩时，水流从进水流道进口进入水泵，流速逐渐升高，在设计流量与大流量工况下进水两侧流速较低，而中间流速相对较高，在设计流量存在小部分漩涡。出水流道流线较为平顺，由于叶轮旋转，导叶出口依然存在一定剩余环量，在出水流道盲端流线呈现为旋转趋势，由速度云图可知，在靠近导叶出口处，水流流速较大且偏向一方，随着水流逐渐排出，流速逐渐降低。对双向流道泵装置流道内增设隔墩后，整流流线影响不大，在设计流量工况盲端，小部分的漩涡被消除，在进水流道，入泵前的水流流速整体得到提高，流速分布相比无隔墩工况更加均匀。出水流道盲端处有旋转趋势的流线得以消除，布置隔墩后，隔墩两侧流速有一定提升。

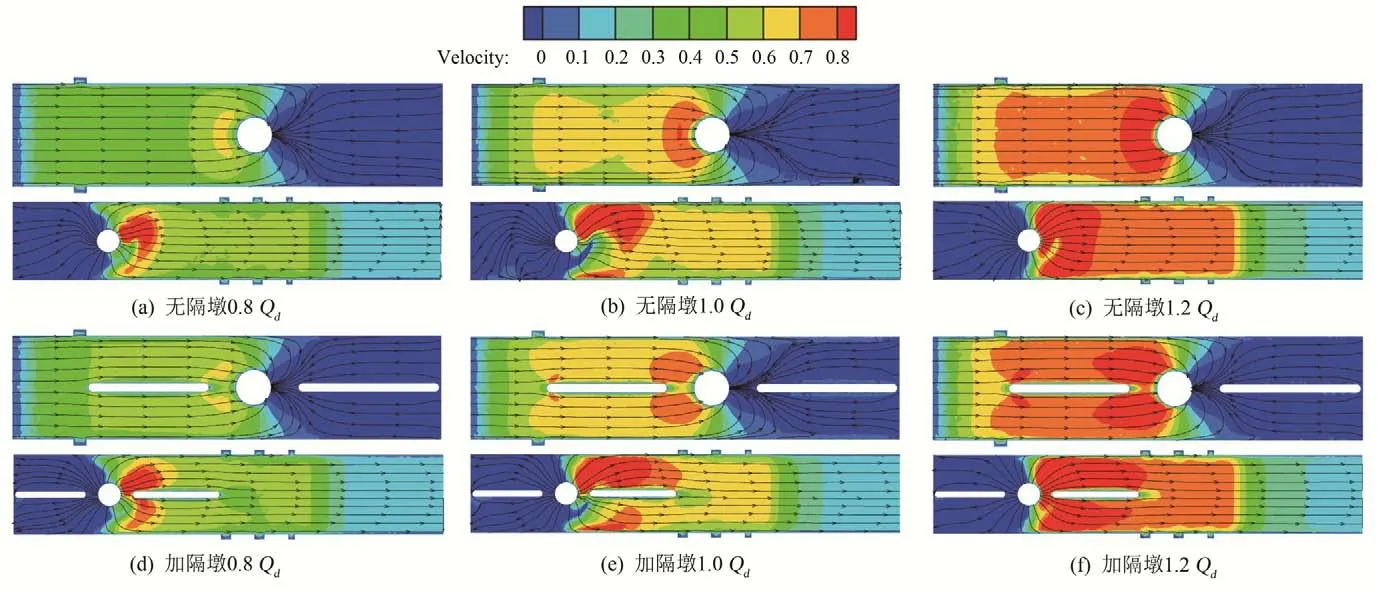
图5 不同工况进、出水流道速度云图及流线图Fig.5 Velocity nephogram and streamline diagram of inlet and outlet passages under different working conditions

采用面积加权的叶轮进口断面流速均匀度进行比较，计算公式如下：

式中：Vuna为断面流速均匀度；vai为叶轮室进口断面各单元轴向速度为叶轮室进口断面的平均轴向速度，m/s；ΔAi为叶轮进口断面i单元面积；A为断面总面积。不同工况下叶轮进口断面流速均匀度计算结果见表1。

由表1可知，在无隔墩与加隔墩各工况，叶轮进口断面流速均匀度均随流量的增大而逐渐增大，对比可知，在进、出水流道加入隔墩后，不同工况下的流速均匀度均有微小提升，在0.8Qd、1.0Qd、1.2Qd运行工况下分别提升0.72%、1.29%、1.36%。

表1 叶轮进口流速均匀度 %Tab.1 Uniformity of flow velocity at impeller inlet

2.2 隔墩对双向流道压力脉动影响

2.2.1 压力脉动监测点布置

为监测双向流道内无隔墩与加隔墩压力脉动情况，在叶轮进口（P1～P3）、叶轮出口（P4～P6）及导叶出口（P7～P9）3个截面沿径向均匀布置3 个监测点，布置隔墩后，流道内水流流态有所变化，在进水流道（P10～P11）、出水流道（P12～P13）盲端处各布置2 个监测点，进水流道（P14～P15）、出水流道（P16～P17）侧壁处各布置2个监测点，具体示意图见图6。

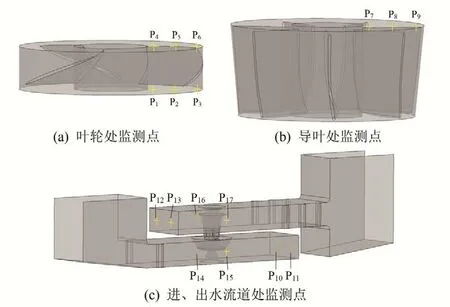
图6 压力脉动监测点布置Fig.6 Layout of pressure fluctuation monitoring points

2.2.2 压力脉动时域分析

通过非定常数值模拟对17 个监测点进行压力脉动数据采集，为了消除监测点自身静压对压力脉动特性影响，采用压力脉动系数Cp来表示其结果，压力脉动系数Cp表达式为：

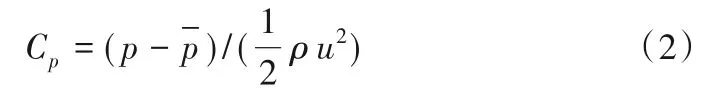
式中：p为监测点静压瞬时值，Pa为监测点静压平均值，Pa；ρ为水的密度，kg/m³；u为叶轮出口圆周速度，m/s。

在设计工况，对加隔墩与无隔墩双向流道内部监测点压力脉动情况进行分析，选取4 个旋转周期进行研究，图7 与图8 分别为无隔墩与加隔墩时设计工况下不同监测点的压力脉动时域特性。由图可知，在流道内加隔墩与无隔墩情况下，叶轮与导叶处压力脉动［图7（a）～（c）、图8（a）～（c）］随时间变化规律相似，均在1 个周期内呈现3 次波峰与波谷，随着测点由轮毂至轮缘的布置，压力脉动系数幅值呈逐渐变大趋势。图7 与图8 对比可知，当流道内无隔墩布置时，进、出水流道盲端及进水流道侧壁［图7（d）～（f）］所布置的监测点测得数据基本重合，而在出水流道侧壁［图7（g）］，由于叶轮旋转作用，出水流道两侧水流流速分布不均匀，所布置两监测点测得脉动数据存在差异，流道内水流流动紊乱，相比叶轮附近无明显脉动规律。增设隔墩后，进水流道盲端与侧壁［图8（d）、（f）］不同监测点数据重合率较高，可以发现，隔墩布置对进水流道内边壁脉动影响较小，对于出水流道盲端与侧壁［图8（e）、（g）］，受导叶出口水流剩余环量影响，流速分布不均匀，而隔墩的布置阻碍了水流流向发展，使不同测点随时间呈现不同的脉动规律，但幅值变化范围差异不大，流道内总体仍无明显波动规律。

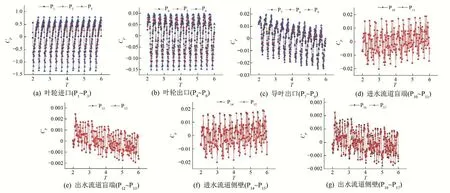
图7 无隔墩设计工况各监测点压力脉动时域Fig.7 Time domain of pressure fluctuation at each monitoring point under design condition without division pier

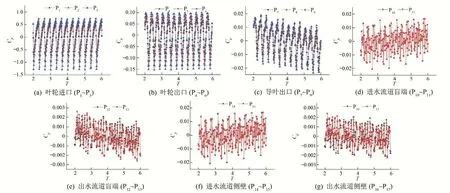
图8 加隔墩设计工况各监测点压力脉动时域Fig.8 Time domain of pressure fluctuation at each monitoring point under design condition with division pier

2.2.3 压力脉动频域分析

将所得数据进行快速傅里叶变换（FFT），得到压力脉动频域特性，图9 为设计工况下流道内无隔墩与加隔墩时各监测点的频谱对比图，其中，布置隔墩采用红色表示，无隔墩采用黑色表示。结果表明，在无隔墩与加隔墩情况下，叶轮与导叶处压力脉动主频与次主频保持一致，均为3 倍转频与6 倍转频，即1倍叶频与2 倍叶频处，由轮毂至轮缘主频与次主频处压力脉动系数Cp逐渐增大，由叶轮进口至导叶出口，主频引起的压力脉动系数Cp逐渐减小。对比有无隔墩结果发现，布置隔墩后主次频不改变，脉动幅值同样无明显变化，可知上述隔墩对叶轮导叶处脉动影响较小。

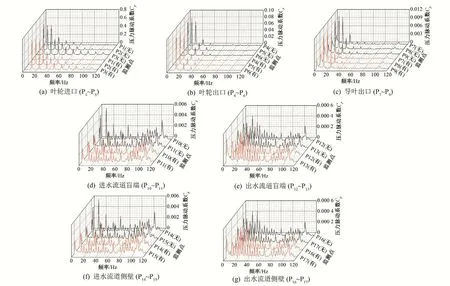
图9 有无隔墩设计工况各监测点压力脉动频域Fig.9 Frequency domain of pressure fluctuation at each monitoring point under design condition with or without division pier

流道内压力脉动规律性较差，图9（d）～（g）表明，在进水流道盲端与侧壁处，布置隔墩后，主频处幅值明显降低，无隔墩时进水流道盲端与侧壁脉动主频为1 倍叶频，压力脉动系数Cp范围为0.006 1～0.006 4，布置隔墩后主频为1 倍叶频，压力脉动系数Cp范围为0.004 1～0.004 2，由于本身压力脉动系数Cp较小，对流道影响不大，在出水流道盲端与侧壁处，隔墩的布置对主次频及幅值影响不大。流道内压力脉动无明显规律，在加隔墩与不加隔墩主次频不一致，但主频仍保持为叶频倍数，其余频率下幅值也相差不大，无隔墩时出水流道盲端与侧壁脉动主频为1 倍叶频，压力脉动系数Cp范围为0.000 56～0.000 58，布置隔墩后主频为2倍叶频，压力脉动系数Cp范围为0.000 53～0.000 56。

3 结 论

通过试验与数值模拟，针对某泵站双向流道内增设隔墩对流道及叶轮导叶处内流与压力脉动特性影响展开研究。主要结论如下：

（1）不同工况下，随着流量增大，流道内流速逐渐增大；在进水流道，流道两侧流速较低，中间较高，布置隔墩后流道内流速分布更加均匀；布置隔墩后，在小流量工况、设计流量工况及大流量工况下流速均匀度也存在少量提升，由82.8%、85.1%、88.3%提升至83.4%、86.2%、89.5%。

（2）压力脉动时域特性表明，叶轮与导叶处脉动幅值呈现周期性变化，1 个周期内均出现3 次波峰与波谷，脉动幅值由叶轮至导叶逐渐减小；增设隔墩后，叶轮导叶处时域特性变化较小，由于隔墩的布置阻碍水流原本运动趋势，出水流道侧壁不同测点时域特性发生改变，但脉动幅值范围相似。

（3）压力脉动频域特性表明，增设隔墩后，叶轮及导叶处主次频及幅值变化不大，而在进水流道盲端及侧壁处，脉动幅值得以降低；流道内压力脉动主要仍在叶频倍数处幅值较大。