基于CEEMD-BP耦合模型的灌区地下水埋深预测

王燕鹏，穆玉珠

（河南省新乡水文水资源勘测局，河南新乡453000）

0 引 言

灌区地下水埋深受气温、降水、蒸发散、地下水补给、地下水开采、土壤地质条件等很多种不确定性因素影响，其演变表现出不确定性、随机性、模糊性以及突变性等特点［1-4］，致使地下水埋深预测困难，且精度较低。提高灌区地下水埋深预测精度，对于灌区水资源合理利用和区域社会经济可持续发展具有重要意义［5-9］。国内外相关学者对地下水埋深预测做了大量研究，并取得了丰硕的成果。Khorasan 等［10］运用长序列模型在地下水埋深预测方面展开了大量研究；Maiti等［11］用多种网络模型对地下水的埋深开展预测并进行了对比分析；Liu 等［12］基于人工神经网络与复杂地下水管理进行了综合研究；Zhou等［13］结合ANN和SVM模型的小波预处理比较分析地下水埋深预测效果；于海姣等［14］运用WA-SVM 模型对我国干旱地区的地下水埋深进行了预测；邵光成等［15］将IABC-RBF 模型应用于地下水埋深预测；曹文洁等［16］将RBF 模型应用到地下水的动态预测中，分析地下水埋深的变化特征。综上可知，国内外的学者对地下水埋深预测的研究主要集中在利用单一模型预测等方面，由于地下水变化受多种不确定性因素影响，致使预测精度较低。互补集合经验模态分解法［17］（Complementary Ensembie Empirical Mode Decomposition，简称“CEEMD”）是一种基于固有模态函数解析的数据分解新技术，通过将数据分解为高频和低频两部分，重而可将复杂的时间序列变化转化为几个简单的单一变量的总和。而BP 神经网络比其他预测模型具有非常好的映射能力［18］，非常适合于非线性和不确定性问题的研究。因此，本文利用CEEMD 和BP 神经网络两者的优点，构建基于CEEMD 和BP网络的耦合模型，并将其应用于人民胜利渠灌区地下水埋深的预测。

1 研究方法

1.1 CEEMD-BP

从CEEMD 分解的角度来看，每个IMF 成分和趋势对时间序列的贡献都不相同，并且可以将IMF 成分和趋势项看成是时间驱动因素。对数据序列进行预测就可以认为对IMF 部分和趋势项两部的预测。

CEEMD-NAR预测步骤为：

（1）CEEMD 分解。利用MATLAB 工具对原始数据进行CEEMD的分解，获得各分量以及趋势项数据。

（2）划分训练数据与预测数据。1993-2011年序列数据的分量和趋势项作为网络的训练数据，2012-2013年序列数据的分量和趋势项作为网络的预测数据。

（3）BP 神经网络预测。利用BP 网络对IMF 分量与趋势项的训练数据进行反复的调试，使BP 分量与趋势项的预测到达最佳的效果。

（4）预测结果分析。最后将预测的IMF 分量和趋势项加起来然后还原，并且和原来的数据进行比较。模型预测流程如图1所示。

图1 CEEMD-BP耦合模型预测流程Fig.1 The technical route of the CEEMD-BP Coupling Prediction Model

1.2 评价指标

预测评价指标选取相对百分比误差RPE、平均绝对误差MAE、均方根误差RMSE、平均相对百分比误差MAPE，和纳什效率系数NSE作为本次预测精度检验的标准。

2 地下水埋深预测

2.1 灌区概况

人民胜利渠灌区是黄河下游首个自流灌溉区，位于河南省的北部，总面积1 486.84 km2。近年来，由于灌区工农业和城市化水平的不断提高，对水资源的需求不断增多，地下水的使用量也在逐步增加，造成地下水埋深日益增加。图2 为人民胜利渠灌区监测井1993到2013年实测数据。

从图2中可知，灌区的地下水埋深每年逐渐增加，但是在增加中还不时有一定的下降，下降的幅度大小也不尽相同，这也说明了埋深序列数据的不确定性和非线性，因此，利用CEEMD在反映非线性问题的优势是可行的。

图2 研究区1993-2013年监测数据Fig.2 Monitoring data of the study area from 1993 to 2013

2.2 CEEMD分解

根据CEEMD 分解的理论与方法，将研究区地下水埋深的数据按照前面所述的CEEMD 分析步骤分解，其中，数据噪声的方差和次数分别取值0.2和100次。结果见图3所示。

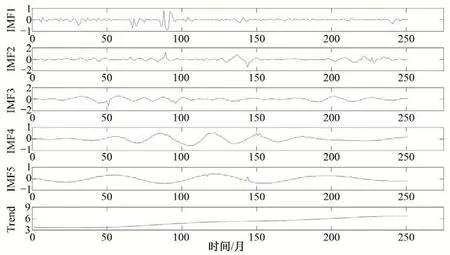
图3 灌区1993-2013年地下水埋深序列CEEMD分解结果Fig.3 Decomposition results of groundwater depth based on CEEMD from 1993 to 2013

从图3 可知，将数据分解成5 个分量和一个趋势项。从分量2 到趋势项波动性逐渐减小，频率也缓慢降低。地下水埋深数据经过CEEMD 分解处理后，平稳性得到了很大的提升，将原来的序列数据分解成具有周期性的分量，从而降低了预测的困难性。

2.3 预测结果

在使用BP 网络预测时，训练样本采用1993 到2011年的分量和趋势项，测试样本采用2012年到2013年的分量和趋势项。采用滚动预测的方式，延时阶数为1∶6，隐含节点数为20。预测结果如图4所示。

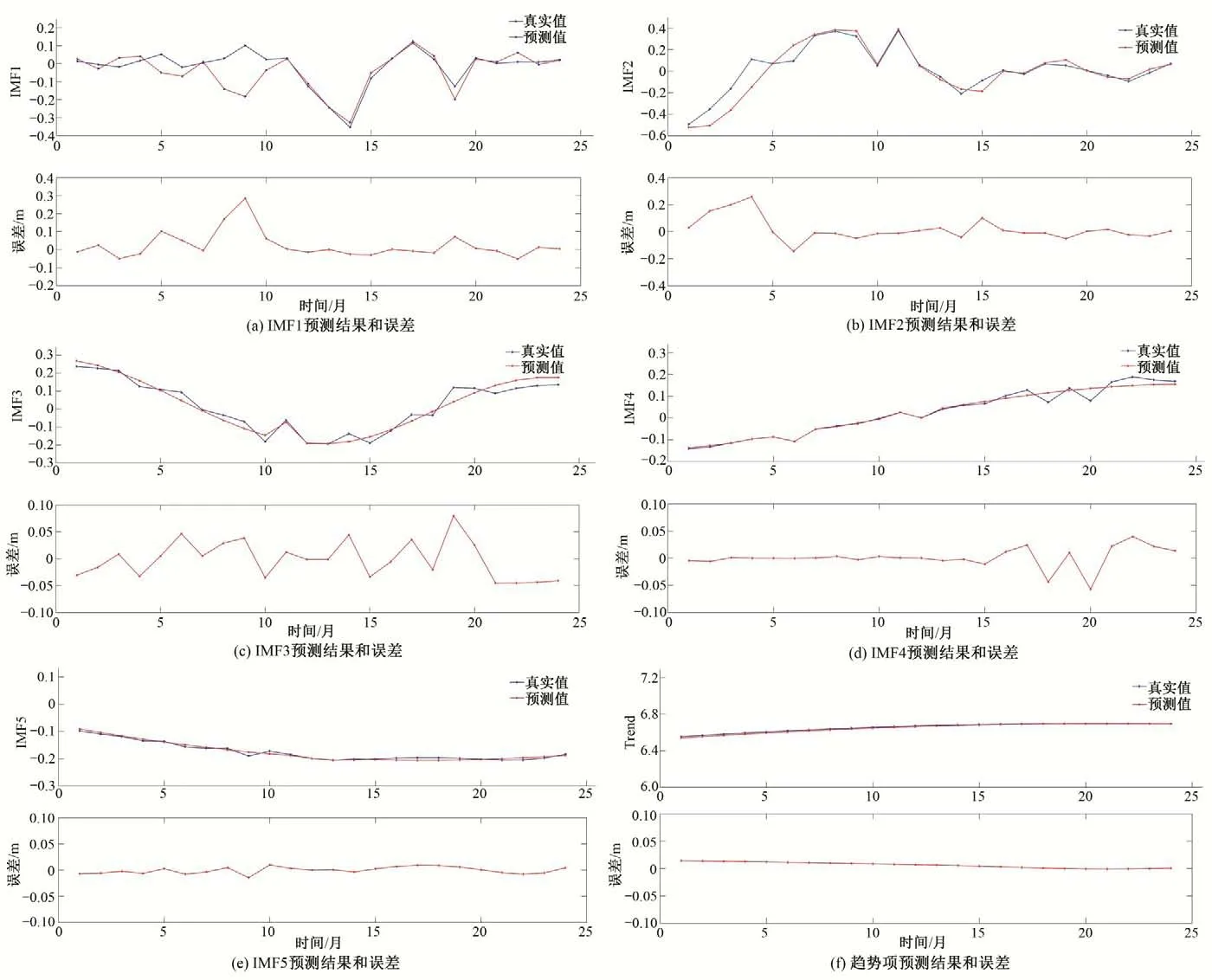
图4 分量IMF1～IMF5和趋势项预测结果Fig.4 Prediction results of IMF1～IMF5 and Residual

由图4 可以得出，分量误差逐渐减小，平稳性相对较高，通过CEEMD 对数据进行分解后，序列数据的波动性大大降低、平稳性显著升高。

由表1 可知，分量一相对误差都比较大，分别是最大值594.74、最小值4.30、平均值161.55，这说明IMF1 分量的平稳性比其他分量要低一点，也对预测误差产生了很大的影响；其他分量误差逐渐减小，逐渐趋于稳定。趋势项所对应的相对误差的各值均较小，分别为最大值0.04、最小值0、平均值0.01，因此低频信号的平稳相对较好，对预测误差产生的影响比较小。

表1 各分量与趋势项相对误差对比 %Tab.1 Comparison of relative error between each component and trend item

由表2 可知，通过计算CEEMD-BP 耦合模型的最大相对误差值为3.04%、最小相对误差值为0.03%、平均相对误差值为0.73%，且计算了模型的纳什效率系数为0.96，接近于1，说明了模型的质量很高，误差较小。

表2 研究区2012-2013年预测的相对误差Tab.2 The relative error of forecast in the study area from 2012 to 2013

由图5 可知，用BP 模型对研究区预测值与真实值基本一致，误差很小，无明显的波动。

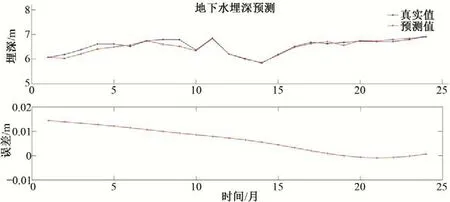
图5 研究区2012-2013年预测曲线Fig.5 Forecast curve for the study area from 2012 to 2013

2.4 讨 论

为了验证CEEMD-BP 的精确性，用Elman 模型、BP 模型、EEMD-BP 耦合模型与CEEMD-BP 模型进行比较。CEEMD-BP模型与其他3种模型对比如表3所示。

由图6可知EEMD 的误差远大于CEEMD；CEEMD-BP 耦合较好的克服了白噪音对EEMD-BP网络误差较大的缺点。

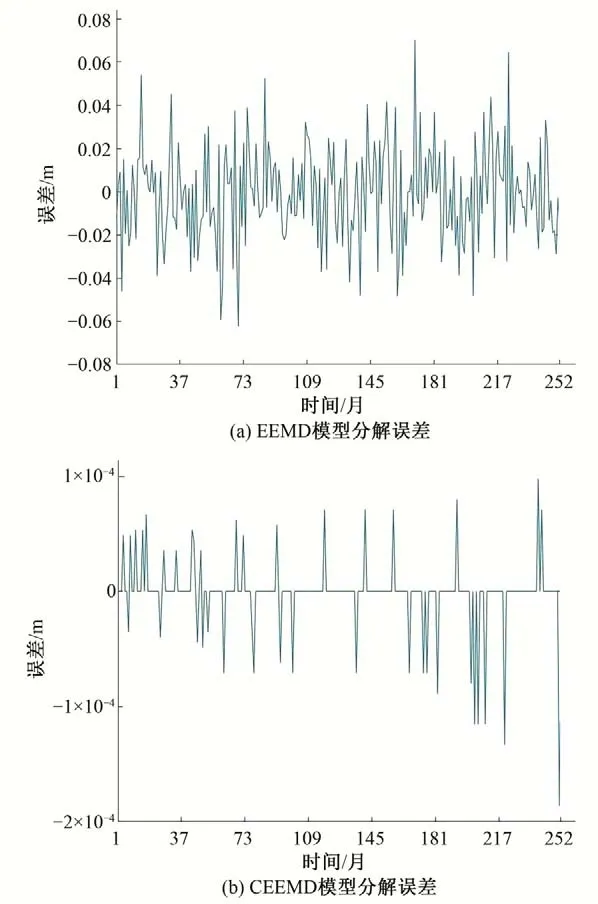
图6 CEEMD、EEMD模型误差Fig.6 The error of EEMD model and CEEMD model

从表3、图7 可知，CEEMD-BP 耦合模型的MAN、RMSE、MAPE均低于其他3 种模型；可以看出该模型与其他的预测模型相比误差小、精度高。

表3 模型评价指标表Tab.3 The outcome of evaluation index

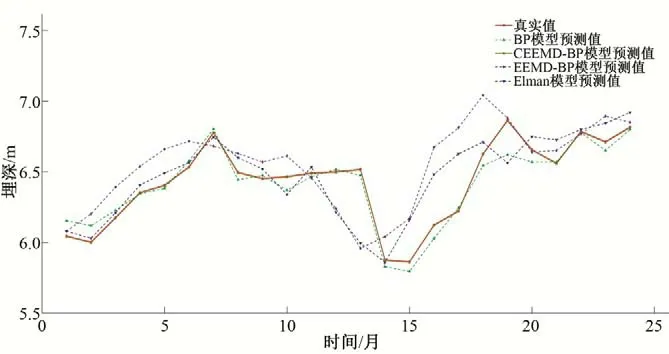
图7 其他模型与CEEMD-BP模型对比结果Fig.7 The outcome of EEMD-Elman model and other models

从图8 可以看出，在预测2012-2013年埋深数据时，同时将Elman、EEMD-BP、BP 模型与CEEMD-BP 相比较可知其相对误差小于其他3种，CEEMD-BP模型的预测效果较好。

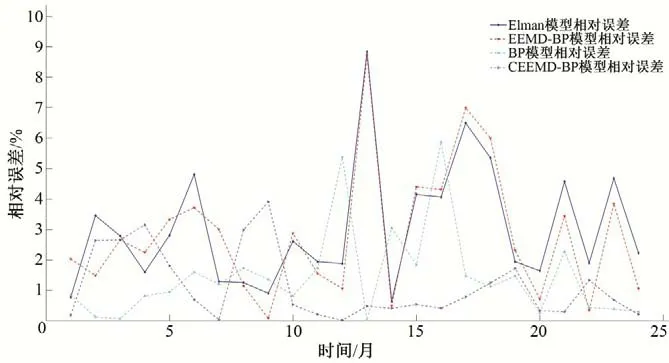
图8 CEEMD-BP与其他几种模型相对误差曲线对比Fig.8 The CEEMD-BP model is compared with other models

3 结 论

（1）地下水埋深经过CEEMD分解，通过增加相反的白噪声，其均值等于0，解决了EEMD 加入单列白噪声。通过将地下水埋深分解成不同频率的子分量，则复杂的预测变成对多个单一的预测变量。降低了原始序列非平稳性，且更具有规律性。

（2）CEEMD-BP耦合模型预测相对误差为0.73%，并计算了常用以验证水文模型模拟结果的纳什效率系数为0.96，精度比其他3 种预测模型相比较高，优于EEMD-BP 模型和BP 神经网络及Elman模型。

（3）虽然CEEMD-BP 耦合模型应用于灌区地下水埋深预测的精度较高，但是对高频分量的预测精度相对较差。另外，模型未涉及地下水埋深演变的物理机制，其适用性及精度的提升仍需进一步深入研究。