基于DT 及PCA 的DNN 入侵检测模型

武晓栋，刘敬浩，金 杰，毛思平

天津大学 电气自动化与信息工程学院，天津 300072

通信系统与网络入口时时刻刻都面临着来自于外部甚至于其系统内部的网络攻击，且不似网络未成熟时期的单一攻击，如今的绝大多数入侵行为种类多样并且呈混合态势发展，防御起来愈发困难。据相关文献，雅虎数据泄露造成了3.5 亿美元的损失，比特币泄露导致了大约7 000 万美元的损失[1]。基于入侵行为，入侵检测可分为基于网络的入侵检测系统（network based intrusion detection system，NIDS）和基于主机的入侵检测系统（host based intrusion detection system，HIDS）[2]。HIDS 通过查看在本地主机上生成的各种日志文件、磁盘资源信息以及系统信息等来检测入侵行为，而NIDS 通过检测出入本地的网络数据流中的数据包来判断是否有入侵行为。机器学习作为近几年非常热门的一种算法工具，理所应当的有专家学者尝试其在入侵检测方面的应用[3]。尤其是近几年，机器学习在入侵检测方面的应用大范围地出现在人们的视野中，从支持向量机（support vector machine，SVM）到神经网络（neural networks，NN）再到随机森林（random forest，RF）都有其在入侵检测中的应用。

1 相关研究

机器学习在入侵检测方面的应用早有先例。2003 年Kruegel 等人[4]将决策树（decision tree，DT）应用到入侵检测中去，相较于当时的Snort 检测引擎[5]能够实现更加迅速的检测速度；2004 年陈光英等人提出了特征选择与SVM 训练模型的联合优化方法，并用入侵检测数据集进行了实验，结果证明联合优化方法能更好地提高SVM 性能,并且有更快的收敛速度，这是国内比较早的一篇利用了机器学习方法的入侵检测相关文献[6]。饶鲜等人基于支持向量机进行入侵检测，对实时性问题进行了研究，但准确率较低[7]。2016 年，Ikram 等人提出利用主成分分析（principal component analysis，PCA）技术降维后用SVM 来检测入侵，其新颖之处在于SVM 中应用了参数自优化技术，提高了分类器的准确率并减少了训练以及测试的时间[8]。2019 年，国内学者杨宏宇等人提出一种基于改进卷积神经网络的入侵检测模型[9]，具有较高的入侵检测准确率与真阳率，且误报率较低。同年，Fernandez 等人提出利用前馈全连接深度神经网络（deep neural networks，DNN）来训练入侵检测系统（intrusion detection system，IDS），由于DNN在动态IP地址分配的情况下表现出鲁棒性，他们所提出的这个模型在现实中有更加广泛的应用范围[10]。仍然在2019 年，刘敬浩等人提出了一种基于ICA（independent component analysis）与DNN 的入侵检测模型ICA-DNN[11]，相较于一些浅层机器学习模型具有更好的特征学习能力和更精确的分类能力,但是对于算法的预测时间并未进行具体评估，模型实时性较差。综合以上学者所提出的入侵检测模型发现大多数研究对入侵检测的实时性研究不够重视，而少数对实时性有较深入研究的入侵检测模型则存在检测准确率不高的问题。为了深入研究对于入侵检测十分重要的实时性问题并保证入侵检测的准确率，本文提出DT-PCA-DNN 模型。训练后的DT 实际上为一系列的if-else 语句，处理大批量数据速度极高，但处理精细度不足；DNN 网络在处理大量高维度数据时的实时性较差，但精细度高。将二者结合，首先用DT 对数据进行一次预过滤再PCA 后送入DNN，实验结果表明，该模型在保证了较高检测率的同时大大提升了训练以及检测速度。

2 基础理论

2.1 主成分分析

PCA 是十分常用的一种线性降维算法，一般用于将高维度的数据的主要成分提取后简化为低维度数据，但是数据的完整程度可以根据需求进行调整。具体而言，PCA 希望将原始的特征空间映射到另外一个正交空间内，而且希望可以使用一个满足最近重构性及最大可分性的超平面来对数据集内所有的数据进行适当的描述。最近重构性：数据集内的点到这个超平面的距离比较近。最大可分性：数据集上的不同点在这个超平面上的投影要尽量远。如图1（a）所示，二维平面上存在若干数据，经由适当基变换（xy→ab），得到图1（b）。在图1（b）中，数据点在原基两个维度的全部信息都包含于a轴，b轴的存在与否不影响数据完整性。由此，实现了二维数据到一维的降维。本次实验所采用的数据集在预处理后维度值为122，经由PCA 降维至11 维，大幅度降低了数据维度间的相关性，简化了计算的复杂性，提供了神经网络所需要的低维数据源。

Fig.1 Diagram of data dimensionality reduction图1 简单数据降维示意图

2.2 决策树

决策树模型是一种描述对实例进行分类的树形结构，由节点（node）和有向边（directed edge）组成，节点有两种类型：表示一个特征或者属性的内部节点（internal node），表示一个类的叶节点[12]（leaf node）。决策树由根节点开始不断依据数据的特征进行分裂，直至所有数据到达叶子节点。作为分裂依据的属性必须是离散属性，对于连续属性，可以按照实验需求将其离散化。某售楼处想要根据对象的身份信息、年龄与是否已婚来判断被调查对象是否有购房需求，调查结果如表1 所示。

Table 1 Respondent information and willingness表1 被调查对象信息意愿表

由此可生成对应决策树如图2，当有对象F 身份为公司职员，已婚，29 岁，可根据决策树得知其有购房需求。

Fig.2 Decision chart of respondent图2 对象决策图

上例中调查对象的特征选择顺序不同，就可以生成不同的决策树。依据选取不同分裂特征有三种判决依据，分别为信息增益、增益率、基尼指数。ID3（iterative dichotomiser 3）算法的核心是在决策树各个节点上应用信息增益准则选择特征，C4.5算法用信息增益比来选择特征，CART（classification and regression tree）则将基尼指数作为选择特征的依据。关于决策树剪枝以及具体特征选择由于篇幅原因不予赘述，参考文献[12]即可。

2.3 深度神经网络

神经网络是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应[13]，此处所说的神经网络指的是机器学习与广义上的神经网络的交叉领域。神经网络中最基础的结构是神经元（neuron）模型，即定义中的简单单元。生物神经网络中，每个神经元与其他神经元相连，当其处于“兴奋”状态时，就会向相连的神经元发送神经递质，从而改变这些神经元的电位。若某个神经元的电位超过了一个“阈值”（threshold），该神经元就会被激活，即处于“兴奋”状态，向其相连的神经元发送神经递质[14]。1943年，国外学者将上述情况抽象为图3 所示的简单模型，即一直沿用至今的“M-P 神经元模型”[15]。

Fig.3 M-P neuron model图3 M-P 神经元模型

在此模型中，xi为来自第i个神经元的输入，ωi为第i个神经元的连接权重，θ为阈值，神经元接收到来自于n个其他神经元传递来的输入信号，这些输入信号通过带权重的连接进行传递，神经元将接收得到的总输入与θ进行比较，通过激活函数f(x)处理得到该神经元的输出y如式（1）：

常用的激活函数有sigmoid 函数、tanh 函数、ReLU 函数[16]。将多个神经元组合在一起即构成了神经网络，拥有超过两层及两层以上隐藏层的神经网络就是所提到的深度神经网络，单纯由输入输出层构成的神经网络只能解决线性可分问题，隐藏层的引入是为了解决非线性可分问题。图4 就是一个全连接的神经网络，即前一层的任一神经元一定与其下一层的任一神经元相连。输入层神经元仅仅是接受输入，不进行函数处理，神经网络的学习过程实质上就是不断调整神经元之间的连接权重与神经元的阈值，从而不断接近训练样本的输出结果，其中最杰出的算法就是误差逆传播（back propagation，BP）算法，现今大多数神经网络的训练都采用BP 算法。

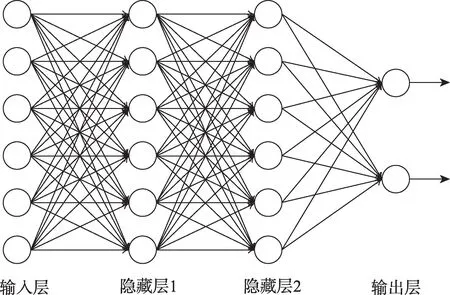
Fig.4 Double hidden layer fully connected DNN图4 双隐层全连接深度神经网络

3 系统设计

系统整体设计如图5 所示，第一步对整体数据集预处理。数据预处理首先将连续数据归一化，其次对离散取值的数据进行one-hot 编码。数据预处理后的数据集分为训练数据集以及测试数据集，用预处理后的训练数据集建立DT 同时训练DNN。PCA 为无监督学习，不需要进行训练，在DT 以及DNN 训练完成后，DT-PCA-DNN 模型建立。此时用经预处理的测试数据集对建立的入侵检测模型进行测试并调整完善相关参数。训练后的DT 实际上为一系列的if-else 语句，处理大批量数据速度极高，但处理精细度不足；DNN 网络在处理大量高维度数据时的实时性较差，但精细度高；PCA 恰好可以解决数据维度过高带来的问题。将三者结合，首先用DT 对数据进行一次预过滤再PCA 后送入DNN 二次分类，用DT 筛选出易判断的入侵数据减轻DNN 工作量，PCA 解决DNN 网络遇到高维数据训练慢的问题，三种方法弥补了彼此的不足之处，在实时性较好的同时保证了检测的准确率。

Fig.5 System flow chart图5 系统流程图

3.1 数据处理

对数据的处理应为两部分，首先将连续数据归一化，其次对离散取值的数据进行编码。

3.1.1 数据归一化

本文实验归一化处理采用min-max 标准化，该标准化方式是对原始数据进行线性变换，变换后数据落入[0,1]区间之内。所用变换函数如式（2）：

设数据集中有m条数据，每条数据都有n维特征，则式中x为归一化前第i条数据的第j维特征值，min为归一化前这m条数据第j维特征中的最小值，max为归一化前这m条数据第j维特征中的最大值，x*为归一化后第i条数据的第j维特征值。

3.1.2 one-hot编码

独热编码，又称为一位有效编码，用于离散数据编码。采用N位状态寄存器来对N个状态进行编码，每个状态都有其独立的寄存器位，且任何时间皆为一位有效。存在样本集合如表2 所示。

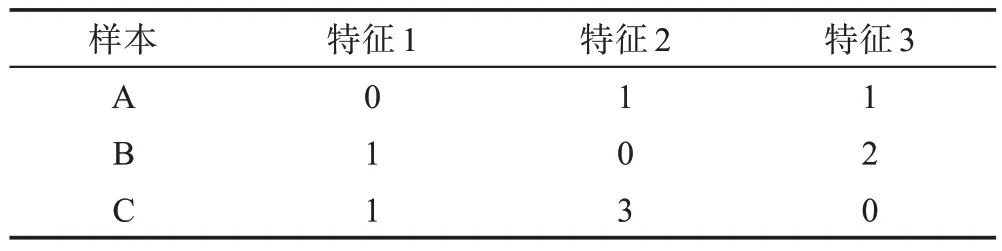
Table 2 Feature distribution of sample set表2 样本集合特征分布表

表2 中的样本特征维度为3，特征1 有两种取值[0,1]，特征2 有四种取值[0,1,2,3]，特征3 有三种取值[0,1,2]。

特征1 有两种取值，则编码规则应为：

0→10

1→01

相应的特征2 有四种取值，则编码规则应为：

0→1000

1→0100

2→0010

3→0001

特征3 的编码规则同上，则不予赘述。

样本A、B、C经过one-hot编码后结果如表3所示。

Table 3 One-hot encoded result of sample set表3 样本集合one-hot编码后结果表

3.2 模型训练

3.2.1 建立DT

首先选择所用决策树类型，因ID3 算法所使用的信息增益对可取值数目较多的属性有所偏好，且所用模型在实验数据未降维之前就使用了DT，数据维度高，因此此处本文选用ID3 算法。其次是DT 的深度问题，由于DT 的作用并不是尽可能多地识别出入侵数据，而是尽可能少地将正常数据误判为入侵数据，DT 的深度不宜过深。如果DT 的深度过深，第一次分类的准确率会有所提升，但是已经被判断为入侵的但实际为正常的数据会影响最终的准确率。

3.2.2 训练DNN

由于DNN 对高维数据进行处理需要比较大的隐藏层层数，一旦隐藏层层数过低，欠拟合现象会十分严重。而隐藏层越多，训练DNN 所耗时间呈指数式增长，与本文的实时性要求不符。引入PCA 对数据进行降维处理后降低了数据特征维度之间的相关性与数据冗余度，DNN 训练更加迅速的同时保证了DNN 的准确率。

DNN 使用BP 算法进行训练，使用ReLU 作为激活函数来简化神经网络的计算过程，使用占用资源少、模型收敛更快的adam 优化算法缩短训练时间。

3.3 DT-PCA-DNN 模型优化

如图6 所示，首先以训练过后的DT 对预处理后的测试数据集初次分类，分类结果为入侵的数据判定为入侵并存入临时训练样本，分类结果为正常的数据去除这次DT 分类所给的标签，准备第二次判断数据类型。DT 这一层相当于过滤网，将易于筛选的入侵数据筛选出来。由于训练后的DT 实际上为一系列的if-else 语句，处理大批量数据速度极高，由此大大减轻了DNN 的工作量，提高了算法的运行速度。

Fig.6 DT-PCA-DNN model optimization图6 DT-PCA-DNN 模型优化

第二步，对DT 判断为正常但已去除标签的数据进行PCA 降维处理。训练后的DNN 对PCA 处理后所输出的低维数据进行第二次分类，分类结果为入侵则添加入侵标签后存入临时训练样本，分类结果为正常则添加正常标签后存入临时训练样本。由于DT 与DNN 属于监督学习，在利用临时训练样本集再训练时需要用到所赋予数据的标签。由于入侵检测过程是逐条数据进行的，可在检测过程中将测试数据集的原本数据类型与所对应数据所添加标签的比对结果进行量化，量化值累积到设定阈值后利用刚才积累的数据对DT 以及DNN 做一次再训练微调。经过若干次的微调之后，所设计模型达到最优。

4 实验仿真

4.1 数据集

本次实验所用数据集为NSL-KDD[17]数据集，它是KDD 99 数据集的改进，相较于KDD 99 数据集，该数据集不包含冗余记录，来自每个难度级别组的所选记录的数量与原数据集内记录的百分比成反比，对所建立模型的评估会更加有效[18]。NSL-KDD 数据集训练集共有125 937条数据，测试集共有数据22 544条，具体的数据类型如表4。

Table 4 Data distribution of NSL-KDD data set表4 NSL-KDD 数据集数据分布表

NSL-KDD 数据集有41 种特征，分为TCP 连接基本特征、主机上的操作特征、基于时间的网络流量统计特征、基于主机的网络流量统计特征这四大特征类；41 种特征的前三种为离散特征，分别为protocol_type（协议类型，共有三种：TCP、UDP、ICMP）、service（服务类型，训练集有70个取值，测试集有64个取值，取二者大值）和flag（连接正常或错误的状态，共11个取值）。

对数据进行归一化处理后进行one-hot 编码。对protocol_type 编码后数据维度上升至43，对service 编码后数据维度由43 上升至112，对flag 编码后数据维度由112 上升至122，最终NSL-KDD 数据集经过onehot编码后的数据维度为122。

4.2 度量指标

首先列出混淆矩阵如表5 所示，TP表示真实数据类型为正常且模型预测结果仍为正常的数据条数，TN表示真实数据类型为入侵且模型预测结果也为入侵的数据条数，FP表示真实数据类型为入侵但模型预测结果为正常的数据条数，FN表示真实数据类型为正常但模型预测结果为入侵的数据条数。当然，仅仅不同数据条数的大小是不足以作为评估实验结果的标准的，因此在以上参数的基础上建立了相对合理的评估标准，即准确率AC（accuracy）、检测率DR（detection rate）、查准率PR（precision）、虚警率FAR（false alarm rate），各自定义分别如下：

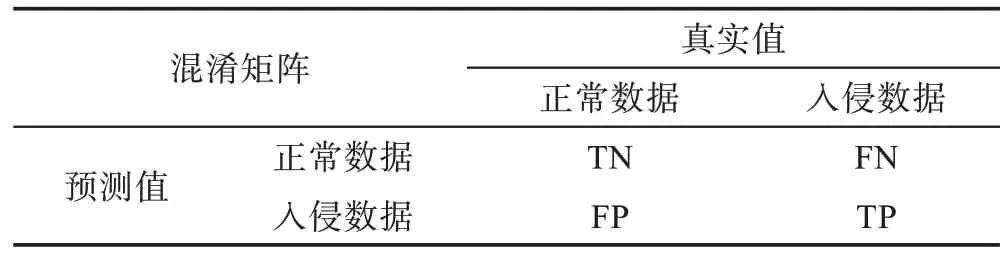
Table 5 Data confusion matrix表5 数据混淆矩阵

4.3 参数设置

对数据进行预处理后，包括one-hot 编码与归一化，所有数据值都位于区间[0,1]，以0.5 为标准对数据各维度进行离散化后用DT 对所有训练数据进行第一次筛选，所用DT 主要参数设置如表6 所示，之后进行PCA 降维，PCA 主要参数设置如表7 所示，降维后数据送入DNN，DNN 主要参数设置如表8 所示。因所设计系统为线性系统，所有参数均可以通过固定其他参数求得该最优参数的方法逐个得出。

criterion（属性切分准则），值为字符串类型，有两种标准可供选择，分别为“gini”与“entropy”。splitter（切分点），值为字符串类型，有两种标准可供选择，分别为“best”与“random”，“best”意味着在所有特征中寻找最优切分点，“random”意味着在随机选择的部分特征中寻找最优切分点。max_depth（所构建决策树的最大深度），可以是整数型或None。max_features为寻找最佳切分时所考虑的特征数。random_state（用以产生随机数的多种状态），其取值可以为整数型、RandomState 实例或None。经实验证明，该值取392时达到最佳效果。

Table 7 PCA main parameters表7 PCA 主要参数

Table 8 DNN main parameters表8 DNN 主要参数

n_components（降维后的特征维度），可以为所降至维度数或者保留数据百分比；whiten（是否白化），使特征之间的相关性减低并且所有特征具有相同的方差；svd_solver（奇异值分解器），字符串，当其值为“auto”，且满足一定条件时，调用完整的奇异值分解函数。

hidden_layer_sizes（隐藏层大小），元组类型。通过调整该值来确定隐藏层层数与隐藏层内的神经元个数。此处引入两个隐藏层，第一层内有140 个神经元，第二层内有70 个神经元；activation 为激活函数；solver（权重优化函数），通过选择不同字符串来选择对应权重优化函数。

4.4 实验结果

实验采用Windows10 系统，64 位操作系统，处理器版本为Intel®CoreTMi7-9750H CPU@2.60 GHz,物理内存总量16.0 GB，开发语言是Python3.5，所用软件包为sklearn。

4.4.1 实验1

本次实验主要研究二分类检测时间，即二分类下检测的实时性问题。本次实验主要对比了FC[19]、DT、PCA-DNN、EDF[20]、CNN[20]、DT-PCA-DNN 模型的二分类预测准确率以及训练时间。为体现DTPCA-DNN 的特点，所用测试数据为NSL-KDD 测试数据集内所有数据。

为便于观察，由表9 得出图7，图中因FC 训练时间过长，对选取纵轴间隔影响过大，不予列出。

Table 9 Results of experiment 1表9 实验1 结果

Fig.7 Results of experiment 1图7 实验1 结果

观 察图7 可 知：PCA-DNN 与FC 的准确率AC 基本相当，但是FC 训练时间远高于PCA-DNN，并且预测时间稍长，检测实时性差。EDF 算法训练时间稍长于PCA-DNN，且准确率AC 与PCA-DNN 基本持平；CNN 算法训练时间长达90 s，准确率也稍低于EDF 以及PCA-DNN，劣于二者。DT 虽然训练速度极快，但是准确率比EDF 以及PCA-DNN 都要低4 个百分点。

较不使用DT 的PCA-DNN，DT-PCA-DNN 训练125 973 条数据多耗时1.32 s，预测22 544 条数据多耗时10 ms 左右，但是准确率AC 有将近10 个百分点的提升，效果十分显著。DT 的引入对训练时间及预测时间的影响极小，但是大大提升了预测的准确率。

4.4.2 实验2

本次实验主要研究DT-PCA-DNN 模型的五分类检测时间，即五分类下的检测实时性问题。将正常样本标记为0，DoS 样本标记为1，Probe 样本标记为2，U2R 样本标记为3，R2L 样本标记为4。

分析表10 可知，DT-PCA-DNN 在五分类上的速度优势是十分明显的，但总准确率稍逊色于EDF 以及CNN，而作为对比的DT 与PCA-DNN，虽然训练时间短，但是相对的总准确率较低，性能不佳。在五分类实验中将PCA-DNN 以及DT-PCA-DNN 进行比较，训练时间长3 s，准确率有6 个百分点的提升，证明DT的引入在保证准确率的同时也并没有造成多大的时间损失。

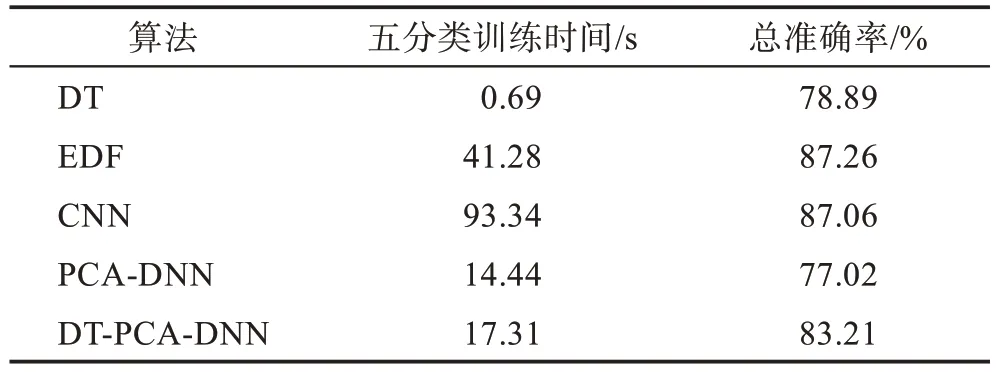
Table 10 Total results of experiment 2表10 实验2 总结果

分析表11 可知，DT-PCA-DNN 在DT 预筛选时可能处理掉了一部分数据导致U2R 无结果显示（U2R 样本量小）。DT-PCA-DNN 的优势主要体现在对R2L 的识别能力上，但因其数据集中占比小，所以导致整体准确率低于EDF 以及CNN，同时该模型对Normal 数据在检测率比较高的情况下虚警率也比较高，这是一个需要指出的问题。

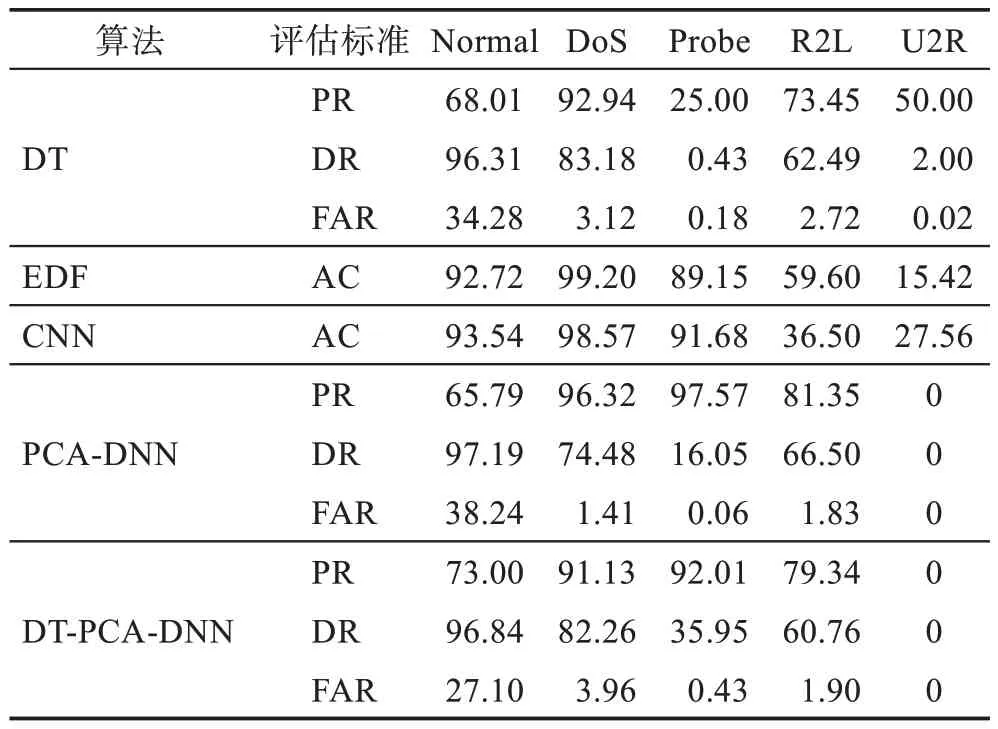
Table 11 Five classification results of experiment 2表11 实验2 五分类结果 %

5 结束语

本文所提出的基于深度学习方法的入侵检测模型DT-PCA-DNN 在保证准确率的基础上大大提高了训练以及检测的速度。模型利用DT 对预处理完毕待检测数据初步筛选再PCA 降维后作为输入由DNN进行二次判决。引入DT 后训练时间增加幅度小，但准确率有了很大提升，同时DT 预筛选减轻了后续DNN 的工作量，对整体训练速度有一定的提升作用。下一步的研究方向主要是解决DT-PCA-DNN 模型在五分类实验中对Normal 数据虚警率高的问题，同时提高DT-PCA-DNN 的五分类能力。