运用数学方法把握关键知识点有效开展总复习

黄惠琦

【摘要】如何有效开展初三中考备考总复习是每一位一线教师面临的共同问题。数学是一门逻辑性强、比较抽象的学科，教师要准确把握关键知识点，运用数学方法开拓学生的思维，有效开展初三总复习。

【关键词】初三数学;总复习;知识点;数学方法;三解形

有效开展初三中考备考总复习是每一位一线教师面临的共同问题。复习课与平时的授课有所不同，它要求对复习目标的把握更准确到位，明确具体，对知识点的梳理简明扼要，更多地关注知识点的内在联系，关注数学思想、方法的渗透、归纳、总结和提升，达到以点带面的高效复习效果。本文将以“三角形的有关概念、性质”复习为例，探讨对关键知识的准确把握以及初三数学总复习的有效开展。

一、准确把握课标要求及复习定位

“三角形的有关概念、性质”是初中数学的重要内容，它包含的基本图形和几何解题方法是中考数学的必考点和频考点。新课程标准对“三角形的有关概念、性质”的知识内容要求也比较高，教师在引导学生复习这一内容时要首先明确课标要求及复习定位，做到有的放矢，提高复习的效率（如图1）。

二、深挖教材，对知识点进行归纳总结提升

教材是学生进行数学学习的根本。在进行总复习时，教师要带领学生深入研究教材，运用数学思想对教材中的知识点进行归纳、总结和提升。

（一）运用分类思想，加深对数学概念的理解

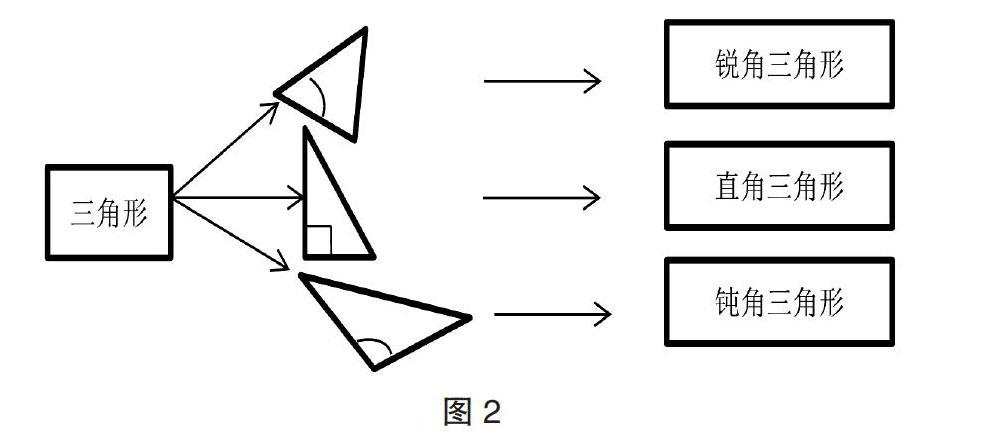
在学习数学概念时，首先要把概念进行分类。分类思想是数学学习中一个非常重要的思想，它可以帮助我们了解新的概念。可以毫不夸张地说，人们对很多事物的认知都是从分类开始的。数学源于生活，在进行“三角形的有关概念、性质”复习时，教师可以在学生了解三角形的定义基础上，运用分类思想画出图形，对三角形进行分类，帮助学生加深对三角形概念的理解（如图2、3）。

1.按角分

2.按边分

（二）感悟化归思想，把未知向已知转化

关于三角形三边关系，教材中有一段精彩描述：“对于任意一个△，如果把其中任意两个顶点（例如B，C）看成定点，由‘两点之间，线段最短可得……”[1]这段描述中隐含了一个重要的数学思想——化归思想。它把探索“三角形三边关系”这个新的问题转化、归结为“两点之间，线段最短”这个已经学习过的知识，从而达到了化未知为已知的教学目的（如图4）。

在学习新知识的过程中，学生是否能运用化归思想将新的问题转化、归结为已学过的旧知识来求解，是学生数学能力的重要体现。新、旧知识之间是有联系的，如果学生能找到它们之间的联系，就很容易理解新的知识。尝试让学生换一个角度看问题，学生就会有新的发现，就会找到新问题的突破口。

（三）构建图形体系，提升识图、作图能力

三角形的高、中线、角平分线是三角形的重要线段，它们之间是有着紧密联系的。在进行复习时，教师可以引导学生找出它们的联系，构建图形体系，提高学生的识图、作图能力。

1.三角形的高

三角形的高起源于垂线段，当它与三角形（锐角三角形、直角三角形、钝角三角形）結合时，就可以得到如下图形（如图5）。过三角形的一个顶点，作三角形的高，其本质就是过这个顶点作对边所在直线的垂线段。只要抓住了这个本质，不论遇到什么三角形都可以轻而易举地作出它的高。高作出来后，一般的三角形就转化为特殊的直角三角形，解题思路也就拓宽了。

由此可见，三角形的高起源于垂线段，可以向直角三角形延伸。三角形的高起到了架构一般三角形和直角三角形的重要作用。

2.三角形的中线

三角形的中线起源于线段的中点，教师同样可以运用构建图形体系的思路让学生对三角形的中线进行深入理解（如图6）。

由构建的图形体系可以找出图形之间的联系，三角形的中线起源于线段的中点，可以向平行四边形、三角形的重心和直角三角形的外接圆图形延伸。

3.三角形的角平分线

三角形的角平分线起源于角的平分线，教师可以引导学生把三角形的角平分线向对称图形延伸，与全等三角形联系起来，还可一生三，生成三角形的内心（如图7）。

从构建的图形体系可以看到，三角形的角平分线起源于角的平分线，可以向全等三角形和三角形的内心延伸。

通过构建图形体系，能够看到图形之间是有联系的，这种联系具有两个发展变化方向：①从简单到复杂，从复杂到简单;②从一般到特殊，从特殊到一般。这样不仅把原本相对独立的知识点联系起来，方便学生进行系统学习、复习，而且可以让学生的识图、作图能力得到有力的提升。

复习课对于即将中考的学生至关重要，它不仅是对已经学过的知识进行系统梳理的过程，而且是让学生掌握重要数学思想的过程。有效的复习课可以帮助学生提高逻辑推理能力、直观想象能力等核心素养，可以帮助学生构建数学知识体系，提高学生分析问题并解决问题的能力。因此，教师要准确把握关键知识点，运用数学方法开拓学生的思维，有效开展初三总复习。

【参考文献】

人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心.义务教育教科书·数学·八年级上册[M].北京：人民教育出版社，2018.