采用自适应优化权重的出库货位优化方法研究

姜良重，雷 航，李贞昊，钱伟中，施甘图

1.电子科技大学 信息与软件学院，成都 610054

2.宏图智能物流股份有限公司，成都 610051

仓库货位匹配作业在现代物流作业系统中占据重要的一环，货位匹配的结果会极大影响整个物流作业的效率和企业利益。不管是人工操作的仓库还是最近流行的自动化立体仓库，都需要一个合理、高效的货位匹配规划。

为了优化货位匹配结果，国内外学者在货位优化方面开展了大量的研究工作。

在优化原则上，Hausman 等[1]提出基于周转率和货物种类的入库货位分配，取得了比随机存储更好的仓库管理效率。党伟超等[2]提出考虑货架稳定性，该方案将货架的稳定性考虑到优化策略中，降低了出入库过程中货架倾覆的风险。

对于货位优化求解算法方面，当今学者大多使用启发式算法，能够在较短时间内，求解出一个令人满意的货位分配结果。Heragu 等[3]提出了使用启发式算法来进行货位分配；马永杰等[4]提出基于遗传算法的自动化仓库货位匹配；俞雷霖等[5]提出基于混合禁忌搜索算法的货位分配，该算法相比传统的遗传算法有着更好的结果表现；陈月婷等[6]提出了改进粒子群算法的立体仓库货位分配优化；张思建等[7]提出了基于模拟退火算法的AVS/RS 多批货箱入库货位优化；王厅长等[8]提出了采用病毒协同进化遗传算法的自动化仓库货位优化方案。

另外，一些学者针对某些特殊场景下的货位分配也进行了大量研究。宁浪等[9]针对JIT生产的零部件配送具有种类多、批次多、批量少、出入库时间分散等特点进行货位优化研究；侯忠等[10]针对汽车零配件仓库特点，采用遗传算法优化货位分配；王雨宁等[11]针对医疗器械仓库具有品类多，需要精准存取等特点，运用EIQBC分类法、多目标指派模型解决货位分配问题。

总之，由于货位分配属于组合优化问题，随着库位的增多，计算量指数级增加，因此国内外学者大多采用启发式算法来优化货位分配，本文对于出库货位优化问题出于计算量考虑同样采用启发式算法。对于优化原则，当前大多数学者研究货位优化问题时，主要考虑货架的稳定性、货物的出入库时间、货物相关性等局限在仓库内部的因素，暂未发现有学者考虑到仓库作业繁忙程度等仓库外部因素对货位优化的影响。在仓库繁忙时，作业人员更愿意优先考虑出库效率，而在仓库作业不繁忙时，作业人员为了降低货物积压导致价值下降风险更愿意出库生产日期靠前的货物，但大多数学者对于存放在仓库内货物的生产日期的考虑，只是简单地使用先进先出原则，无法满足作业人员要求。

本文基于以上发现的不足，首先设计货物剩余价值率和出库代价优化模型，然后基于仓库作业的繁忙程度，研究仓库繁忙程度对货物出库代价和货物剩余价值率之间的优化权重取值的影响，提出了基于仓库繁忙率的自适应优化权重，并建立多目标出库货位优化模型，接下来，使用基于自适应算子，灾变算子和精英策略的改进策略的遗传算法对模型求解，并基于企业实际数据验证模型和算法的合理性，最后总结本文研究成果。

1 出库货位分配多目标优化模型构建

1.1 货物剩值率设计

货物剩值率是货物的当前实际价值与刚生产时价值的比值，影响货物剩值率的因素主要有货物是否有损坏，临近保质期程度等，由于货物仓储中损坏概率小，故本文只考虑临近保质期程度对货物剩值率的影响，并定义临期率衡量货物临近保质期程度。

货物刚生产的一段时间内，价值变化不大，但到某临界点后，价值会逐渐下降，并且下降速度会随着时间推移而加快。因此，定义第i种货物的第n批次的货物的临期率Rexpri(i,n)如式（1）：

式（1）中，Psl(i,n)是第i种的第n批次的货物的剩余保质时长，Pl(i,n)是第i种货物的第n批次的货物的保质时长。

基于以上分析，第i种货物的第n批次的货物剩值率Rrv(i,n)如式（2）：

为了在出库过程中优先出库货物剩值度低的货物，第一个优化目标函数如式（3）：

式（3）中，SorderSku是订单货物种类集合，SResult(i)是第i种货物的货位分配结果集，A(i,n)是第i种货物的第n批次货物的数量，AorderSum是订单要求货物数量总和。

1.2 货物出库代价设计

货物出库代价是衡量某订单需求货物出库时需消耗的总时间代价。本文暂只针对立体仓库研究，故定义编号为z的库位，库位中存放第i种货物的托盘的出库代价C(z,i)如式（4）：

式（4）中，Dh(z)是编号z的库位到门的最短路径距离，Vfork是叉车速度，Nl(z)是编号z的库位所在的层数，Televator是升降机每升/降一层需要的时间。

根据上述分析，为了尽可能降低出库代价，故建立第二个目标函数如式（5）：

式（5）中，SorderSku是订单货物种类集合，Sresult是货位分配结果集，N(z,i)是编号为z的库位中含第i种货物的托盘数，C(z,i)是编号为z的库位存放第i种货物的托盘的出库代价。

1.3 多目标优化倾向权重确定

出库货位优化目标有货物出库代价和货物剩值率，当仓库繁忙时，货位优化算法应更倾向于优化出库代价，提高作业效率，防止仓库拥挤；当仓库作业空闲时，货位优化算法应更倾向于优化货物剩值率，将货物剩值率低的货物出库，降低货物因存放过久而价值下降的风险。

基于以上分析，本文使用仓库繁忙度衡量仓库繁忙程度，并根据仓库繁忙度计算各优化目标的权重。

1.3.1 仓库繁忙度计算方法

仓库繁忙度是指开始进行货位优化的那一时刻的仓库繁忙度。仓库出库操作主要靠叉车，叉车使用率高，则说明当前仓库作业繁忙。因此，采用叉车使用率来衡量仓库繁忙程度，但考虑在当前出库作业过程中仍可能有作业到达，因此不能仅考虑某一时刻仓库叉车使用率。

基于以上分析，某一时刻仓库叉车使用率Rforkuse表述如式：

式（6）中，NcurFork是当前仓库正在使用的叉车，NsumFork是仓库中总共拥有的叉车数量。

仓库繁忙度MwarehouseBusy表述如式（7）：

式（7）中，λ是考虑到当前出库作业过程中仓库繁忙度增加而设置的预留量，设置为0.2。

1.3.2 倾向权重计算方法

本文选用线性转换得到货物剩值率优化倾向权重w1和货位出库代价优化倾向权重w2，表述如式（8）：

1.4 目标函数归一化处理

由于任务总量、货物种类等因素会导致f1和f2的值相差较大，f2根据定义不需要进行归一化，因此仅需对f1进行归一化处理。

货物的出库代价由于出库库位位置和数量的不确定性，在全局上无法进行归一化处理，因此本文根据遗传算法特点，在每一代种群内对f1进行归一化处理。

基于以上分析，在某一代种群内，f1和f2归一化后的fn1和fn2表述如式（9）：

式（9）中，fmin1是当代种群中f1的最小值，fmax1是这代种群中f1的最大值。γ是常量，防止分母为零，设置为0.000 1。

1.5 出库货位优化模型目标函数

出库货位优化模型需要满足如下几个约束：所选库位的货物数量和种类必须满足订单要求；所选库位的货物能够被允许出库。

基于以上分析，得到优化目标函数表述如式（10）和（11）：

式（10）中，Fout是优化函数值，fn1是f1归一化后的值，fn2是f2归一化后的值。式（11）中，A(i,z)是编号为z的库位上第i种货物的数量，AorderSum(i)是订单要求的第i种货物的数量，F(i,z)是编号为z的库位上第i种货物能否出库标志。

2 出库货位优化模型的算法设计

出库货位优化涉及出库货位选择和货位货物出库顺序确定。因此参考文献[12]，将货位优化问题分为两层进行优化：（1）货位选择层：选择哪些库位上的货物完成货物出库；（2）货位顺序层：确定已选中的货位货物出库顺序。

2.1 货位选择层算法设计

货位选择层优化问题是组合优化问题，采用遗传算法进行求解。因已有研究成果表明精英策略[13]、自适应交叉率[14]和变异率和灾变算子[15]明显改善了传统遗传算法的缺点，因此这里基于上述改进策略并结合货位优化问题特点设计货位选择层算法。

2.1.1 确定编码方式

染色体采用二进制编码，染色体中每个基因表示一个库位，1代表选用该库位货物，0代表不选用该库位货物，染色体长度为货物对应库位数总和，并使用辅助编码表达每个基因所对应的库位、货物类别、数量信息，染色体结构设计如图1所示。

图1 染色体结构Fig.1 Chromosome structure

2.1.2 适应度计算设计

因出库货位优化是最小化目标函数而适应度是求最大值，需要转换，因此，适应度函数表述如式（12）：

式（12）中，Fadapt是适应度值，Cmax是一个相对大的数，Fout是出库货位优化目标函数，因Fout最大值为1，因此设Cmax=1。

2.1.3 选择算子设计

先采用精英策略，将种群中适应度最大的个体直接复制进入下一代，对于剩余个体采用锦标赛选择法选择，两种策略结合既能不丢失最优个体，又能保证适应度较大个体的基因遗传到下一代。

2.1.4 自适应算子

自适应算子能提高遗传算法的收敛精度和收敛速度，本文自适应算子参考文献[16]，如式（13）：

式（13）中，k1、k2、k3和k4是常量，fmax是当前种群中个体最大适应度值，f′是要交叉的两个个体中较大的适应度值，favg是当前种群平均适应度值，f是要变异个体的适应值，Pc是交叉概率，Pm是变异概率。

2.1.5 交叉算子设计

基于编码特点和出库货位分配问题特点，交叉方式采用同类货物基因段双切点交叉。同类货物基因段双切点交叉操作过程如下：

步骤1在种群中，随机选取父代个体PL1和父代个体PL2。

步骤2在PL1上随机选取一段同类货物基因段。

步骤3将PL1和PL2上相同位置的同类货物基因段进行互换。

这样操作的优点是两染色体交叉后，子代染色体所表示的结果仍符合优化目标的约束。

2.1.6 变异算子设计

针对染色体编码方式和出库货位分配问题特点，采用互换变异方式。首先，随机在染色体上，选取一段同类货物基因段，然后在该基因段上随机选取一个值为1的基因和一个值为0的基因，最后将两个基因值互换。

2.1.7 染色体修复策略

由于每个库位的货物数量不同，在进行变异操作后，可能导致染色体无法满足出库货位优化目标的约束，需要进行染色体修复，修复步骤如下：

步骤1首先，判断经过变异的第i种货物对应染色体基因段Gi所表达的货物数量是大于、小于还是等于订单中第i种货物的数量。若小于转步骤2，若大于转步骤4，若等于转步骤5。

步骤2变异后导致基因段Gi所表达的货物数量小于订单中第i种货物的数量，需要增加出库库位，从未选择的出库库位中随机选择一个库位SnoSelect，将基因段Gi中对应库位SnoSelect的基因值变为1，转到步骤3。

步骤3判断基因段Gi所表达的货物数量是否小于订单中第i种货物的数量，若大于转步骤5，否则转步骤2。

步骤4变异后导致基因段Gi所表达的货物数量大于订单中第i种货物的数量，可能需要减少出库库位，将基因段Gi里基因值为1所对应的库位按照库位存放第i种货物的数量从小到大排序成S1,S2,…，然后依次按顺序累加库位Si存放第i种货物的数量，若累加的货物数量大于订单中第i种货物数量，则将库位Si后面的库位所对应基因段Gi的基因值变为0，即不选择后续库位。转步骤5。

步骤5结束染色体修复。

2.1.8 灾变算子设计

灾变算子的引入，模拟了自然界中生物灭绝现象，其主要作用是当算法过早收敛时，使其跳出局部搜索。灾变算子主要由灾变条件和灾变方式构成，本文设计如下：

（1）灾变条件：首先设置一个灾变倒计时数C，每当新一代个体中最好的个体的适应度相比上一代没有进化，则C值减1；然后当C=0，发生灾变，根据灾变方式重新生成种群。

（2）灾变方式：首先保留当代最优个体，然后随机生成其他个体，最后将这些个体组成新一代种群。

2.2 货位顺序层优化

货位顺序层优化是基于货位选择层优化结果进行优化，确定货位上货物出库顺序。

2.2.1 货位顺序层问题描述

由于订单要求货物数量不一定恰好等于所选库位上存放的货物数量，导致最后一个出库的库位上货物只有部分货物出库，若随机确定顺序，可能导致出库货位优化结果不佳，因此需要确定货位出库顺序。

2.2.2 货位顺序层优化算法设计

首先确定存放货物需全部出库的库位，然后对剩余的每个库位计算每个库位的出库优化目标值，最后根据每个库位的出库优化目标值从小到大依次选择库位。基于以上思想，设计如下步骤来求解货位顺序优化问题：

步骤1按照库位上存放第i种货物存放数量从大到小排序得库位序列(S1,S2,…,Sn)，依次累加库位上第i种货物的数量，直到总和满足订单中第i种货物数量，剩余没有被累加的库位序列(Sm,Sm+1,…,Sn)为货物全部出库的库位，库位序列(S1,S2,…,Sm-1)则为需要比较的优化目标大小的库位。转到步骤2。

步骤2针对库位序列(S1,S2,…,Sm-1)，计算每个库位的出库优化目标值。转到步骤3。

步骤3步骤2 中计算的库位出库优化目标值最大的库位为最后出库库位，(Sm,Sm+1,...,Sn)库位序列根据库位存放第i种货物的数量由小到大顺序出库。

2.3 出库货位优化模型求解算法流程

出库货位优化模型求解算法需要经过货位选择层算法优化和货位顺序层算法优化，流程如图2所示。

图2 出库货位优化模型求解算法流程图Fig.2 Flowchart of algorithm for solving outbound storage location optimization model

3 实例验证和结果分析

3.1 实验环境

本文使用Java 语言实现出库货位优化算法并基于实际生产数据进行算法验证。

参考遗传算法常用参数设置，设置出库货位优化算法参数如表1所示。

表1 出库货位优化算法参数表Table 1 Parameter table of outbound storage location optimization algorithm

3.2 实例数据

本文数据来源于宏图智能物流股份有限公司的物流仓库数据库中的货物存储数据，数据格式见表2。

表2 库存信息格式Table 2 Inventory information format

数据库中信息含有8 165 个库位信息，19 588 个不同货物种类不同批次的货物库存信息，总库存货物数量为11 222 825件。

3.3 实验结果分析

3.3.1 验证算法性能

本文基于自适应算子、精英策略和灾变策略的改进出库货位优化算法（IOSAA）是对采用标准遗传算法的传统出库货位优化算法（TOSAA）的改进，现基于实际订单运用IOSAA 和TOSAA 分别对货物出库货位分配模型进行求解，并比较目标函数值的结果来验证IOSAA是否比TOSAA有更好的优化结果。由于出库代价无法在算法外部进行归一化，因此，将出库代价倾向优化权重设为1，比较两者优化出库代价的结果，实验采用的订单详情如表3所示。

表3 测试实例中订单详情表Table 3 Order details table in test case

算法优化过程对比结果如图3所示。从图3可以看出，TOSAA由于采用传统遗传算法作为主要优化手段，导致无法保存每一代最优结果，因此优化过程不平稳，并且容易过早收敛，无法继续优化；而IOSAA由于采用了精英策略、自适应算子和灾变算子改进手段，可以弥补传统遗传算法的不足，优化过程更平稳、快速，并且可以避免过早收敛，尽可能到达到最优值。

图3 IOSAA和TOSAA优化过程比较Fig.3 Comparison of IOSAA and TOSAA optimization process

下面采用了10个不同的企业实际出库订单再次对比IOSAA和TOSAA算法效果，出库代价倾向优化权重设为1，结果如图4所示。

图4 不同订单下IOSAA和TOSAA出库代价优化结果对比Fig.4 Comparison of IOSAA and TOSAA outbound cost optimization results under different orders

从图4 可以看出，IOSAA 的优化结果明显优于TOSAA，在各个订单中都表现稳定，出库代价最低，并且随着订单规模增加，出库代价增大，差距也越明显。

下面结合自适应优化权重，对比IOSAA和TOSAA，设置仓库繁忙度为0.6，出库代价和剩值率结果如表4所示。

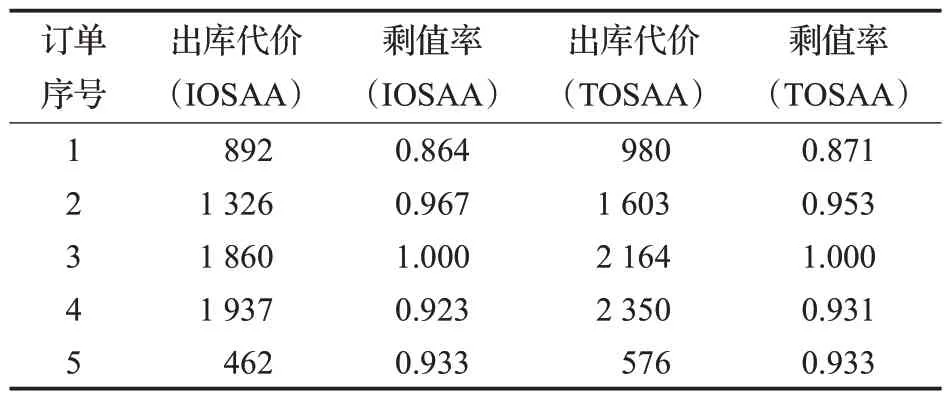
表4 基于自适应优化权重，IOSAA和TOSAA结果对比Table 4 Based on adaptive optimization weights，IOSAA and TOSAA results comparison

为了明显看出两者的差距，定义对比综合值如式（14）：

式（14）中，Fcompare1是算法1 的对比综合值，Fcompare2是算法2的对比综合值，fout1是算法1结果中的出库代价，fout2是算法2结果中的出库代价，frv1是算法1结果中的货物剩值率，frv2是算法2结果中的货物剩值率。

因此，表4 中IOSAA 和TOSAA 所对应的对比综合值，如表5所示。

表5 表4中IOSAA和TOSAA所对应的对比综合值Table 5 Value of comparison of IOSAA and TOSAA in Table 4

从表5 可以看出，IOSAA 的对比综合值明显小于TOSAA，优化结果表现更优。

由于货物出库过程中作业人员无法忍受算法耗费过长时间，因此接下来比较两者运行时间，通过运行100次，TOSAA和IOSAA平均运行时间对比如图5所示。

图5 IOSAA和TOSAA运行时间对比Fig.5 IOSAA and TOSAA running time comparison

如图5 所示，TOSAA 算法运行速度要快于IOSAA算法，但是对于实际应用来说，100多毫秒的延迟相比于优化结果的提升幅度，是完全可以接受的。

基于上述分析，表明改进后的出库货位优化算法能够有效解决出库货位优化问题，并且优化结果相比使用标准遗传算法的出库货位优化算法有所提高。

3.3.2 验证自适应优化权重作用

为验证基于仓库繁忙度的自适应优化权重是否有效，本文首先选取同一个订单，采用不同的仓库繁忙度，分别使用自适应优化权重和不适用优化权重算法进行对比，仿真结果如图6所示。

图6 同一订单不同仓库繁忙度下，仿真对比结果Fig.6 Simulation comparison results under the same order with different warehouse busyness

接下来选取一系列订单，采用同一个仓库繁忙度（这里设置仓库繁忙度为0.6），分别使用自适应优化权重和不适用优化权重算法进行对比，仿真结果如图7所示。

图7 不同订单同一仓库繁忙度下，仿真对比结果Fig.7 Simulation comparison results under the same warehouse busyness for different orders

由图6、图7的结果可知，使用了自适应优化权重的出库货位优化算法对于货物剩值率的优化优于不使用自适应优化权重的算法，这是由于不使用自适应优化权重的算法只考虑优化出库代价，这导致某些生产日期靠前的货物无法出库，造成货物积压，给企业造成损失，而使用了自适应优化权重的出库货位优化算法根据仓库繁忙度来调整优化权重，并且在仓库繁忙时，倾向于降低出库代价，提高出库代价；在仓库比较空闲时，倾向于出库货物剩值率低的货物。因此，基于仓库繁忙度的自适应优化权重可以有效帮助仓库降低生产日期靠前的货物积压风险，同时可以在仓库繁忙时优先考虑出库效率。

4 结语

本文研究了仓库出库货位优化问题，建立了以出库代价和货物剩值率为原则的出库货位优化模型，并利用改进遗传算法结合基于仓库繁忙率的自适应优化权重对模型进行求解，通过企业实际生产数据验证了模型和算法的可行性和合理性，对于出库货位优化，采用精英策略、自适应算子和灾变算子的遗传算法的优化结果优于标准的遗传算法，并且其收敛速度更快，能够避免过早收敛；同时使用基于仓库繁忙率的自适应优化权重，能够较好地避免货物因在仓库内存放过久而货物价值降低的风险同时又能在仓库繁忙时优先考虑出库效率。

本文在研究中对于临期率和货物剩值率的设计过于主观，并且没有考虑到跨仓库出库的情形。因此，在今后的研究中，需要进一步研究，建立更加客观的临期率和货物剩值率模型，并研究跨仓库出库的场景下的出库货位优化。