支持连接关键词搜索的属性加密方案研究
2021-08-06陈思琦黄汝维
陈思琦,黄汝维
(广西大学计算机与电子信息学院,广西 南宁 530004)
1 引言
在云计算模式下,用户将存储或者计算任务外包给云服务器,就能够享受高质量的存储服务或计算服务。为了保证隐私安全,用户通常将数据加密后进行存储。可搜索加密技术使得用户能够在不解密的前提下对密文进行检索操作,用户将数据加密后存储在云端,提出搜索请求的用户利用搜索关键字生成陷门,云服务器执行关键字搜索任务,然后返回包含该关键字的密文。大部分的可搜索加密方案属于“一对一”通信模式,在云计算环境下,用户希望能给特定的一部分人分享数据,数据拥有者要么对密钥进行共享,这显然会带来密钥泄露的可能性;要么每增加1个用户,均使用该用户的公钥对数据进行加密,这使得数据拥有者加密负担较重;或者通过聚合密钥等操作,当用户逐渐增多时,可信授权机构管理密钥的负担也会增加。在大部分单关键词可搜索加密方案中,如果第1次搜索返回的结果无法满足用户需要,用户将会使用另外的关键词进行下一轮搜索,这种多次搜索-解密的过程将会花费很大的代价。
在多用户数据共享方面,2005年,Sahai等人[1]提出了基于属性的加密方案ABE(Attribute-Based Encryption)。基于属性的加密方案主要分为密钥策略的属性加密方案KP-ABE(Key-Policy Attribute-Based Encryption)和密文策略的属性加密方案CP-ABE(Ciphertext-Policy Attribute-Based Encryption)。在CP-ABE中,密文与访问策略相关联,适合云环境下数据分享场景,数据属主制定访问策略,用户的属性用来生成私钥,满足访问策略的用户能够解密相应的数据。Goyal等人[2]提出了一个基于访问树结构的KP-ABE方案。Kaushik等人[3]于2013年构造了基于CP-ABE的可搜索加密方案,采用了访问树结构。大部分基于访问树的可搜索加密方案虽然能够直观方便地表达访问策略,但是存在计算开销、通信开销较大等问题。2011年,Waters[4]提出了3种基于不同困难假设的CP-ABE方案,基于线性秘密共享策略LSSS(Linear Secret Sharing Scheme),实现了与访问树相等的策略表达能力,且具有更高效率和安全性。陈燕俐等人[5]提出了一个基于LSSS共享矩阵的可搜索加密方案,能够支持文件级细粒度的访问控制。部分其他基于CP-ABE的加密方案主要针对属性撤销、提高加解密效率方面[6 - 9]。
为了缩小搜索范围,避免多次搜索-解密的过程,Golle等人[10]提出了2种支持连接关键词的搜索方案。Chuah 等人[11]于2011年提出了基于 Bed Tree的多关键词搜索方案,提高了搜索效率。王尚平等人[12]提出了支持关键词连接搜索的加密方案,并且通过授权用户以及云服务器先后对关键词加密来实现多用户共享。但是,文献[10-12]的方案基于对称密码学,实用性有限。Boneh等人[13]基于谓词加密概念,构建了支持加密数据上的比较查询(x≥a)公钥系统,实现加密数据上的连接关键词搜索,但是该方案使用合数阶双线性群,需要较大的群空间。2012年,Chen 等人[14]提出了2种支持关键词连接搜索的加密方案,但是该方案无法支持关键词子集的搜索。Zhang等人[15]提出了支持关键词子集搜索的加密方案,但是用户端的计算量较大。宋衍等人[16]提出了一个支持关键词任意连接搜索的属性加密方案,在方案中使用了访问树作为访问结构,当文档数据较多时,加解密效率仍然有待提高。
针对大部分基于属性的可搜索加密方案存在效率低下、密钥易泄露以及仅支持单关键词搜索的问题,本文基于LSSS提出了一个支持连接关键词搜索的属性加密方案AECKS(Attribute-based Encryption supporting Conjunctive Keyword Search),能够支持文件级细粒度访问控制,提高用户的加解密效率。基于多项式方程实现了连接关键词的搜索,使得搜索范围更加精确,提升了用户的搜索体验。
2 基础知识
2.1 双线性群
设p、q是素数,G1、G2分别是阶为p、q的乘法循环群,双线性映射e:G1×G1→G2。则有:
(1)双线性。对于任意的a,b∈Zp和x,y∈G1都有e(xa,yb)=e(x,y)ab;对于任意的x1,x2,y∈G1,有e(x1x2,y)=e(x1,y)e(x2,y)。
(2)非退化性。存在x,y∈G1,使得e(x,y)≠1,其中1是G2的单位。
(3)可计算性。存在有效的多项式时间算法对任意的x,y∈G1,计算e(x,y)的值。
2.2 q维判定性Diffie-Hellman问题(q-DDH)

2.3 Shamir秘密共享方案
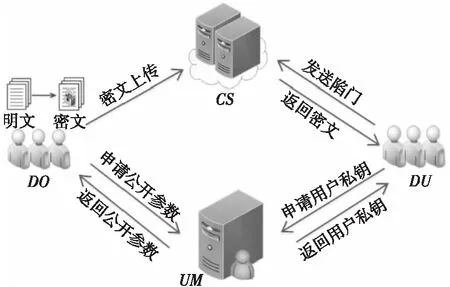
Shamir秘密共享方案基于拉格朗日多项式插值,设p为素数,共享秘密值为s。通过tt个子密钥重构得到共享秘密值s,当t′ 给出tt个子密钥yi,i≤i≤tt,通过拉格朗日插值公式重构出多项式f(x)为: (1) AECKS方案的系统模型如图1所示,包括授权管理机构(UM)、数据拥有者(DO)、数据用户(DU)和云服务器(CS)共4个参与方。UM负责管理系统中的全部属性,并且负责系统初始化和用户密钥生成工作,UM是完全可信的;DO首先对文档的每个文件生成关键词集合,使用访问结构将关键词集合进行加密,文档数据利用对称加密算法加密(如AES加密算法),然后将所有密文上传到CS;DU根据搜索需要,利用私钥以及想要搜索的关键词集合生成陷门后发送给CS;CS负责用户数据存储以及数据搜索工作,CS是“诚实但好奇”的,能够忠实执行用户的操作,但可能会试图从中获取信息。 Figure 1 System model图1 系统模型 支持连接关键词搜索的属性加密方案AECKS包括下列5个多项式时间算法: (1)Setup(1λ)→ (PK,MSK):由UM执行初始化算法,生成系统公私钥。UM输入1个安全参数1λ,输出1个公钥PK和1个主密钥MSK。 (2)Encrypt(PK,(M,ρ),W)→ (CT):由DO执行加密算法。算法输入公共参数PK、用户定义的访问结构(M,ρ)和待加密的关键词集合W,输出密文CT,其中ρ为2.4节中的映射函数。 (3)KeyGen(PK,MSK,S)→ (SK):由UM执行用户私钥生成算法,算法以公共参数PK、系统主密钥MSK以及用户属性集S作为输入,输出用户私钥SK。 (4)TokenGen(SK,W′)→ (Trap):由DU执行陷门生成算法,输入用户私钥SK和待搜索的关键词集合W′,输出W′对应的陷门值Trap。 (5)Search(CT,Trap): 由CS执行关键词搜索算法,输入密文CT和陷门值Trap,如果用户满足数据属主定义的访问策略且搜索的关键词集合存在,则CS返回对应的搜索结果,否则CS返回0。 PK=(e,p,ga,gb,{hi}i∈[1,|U|]G,GT,H) (2) 保存主密钥为: MSK= (a,b) (3) z(x)=a·(x-H(w1))(x-H(w2))… (x-H(wmp))+k= ampxmp+…+a1x+a0 (4) 对于i∈{ 0,1,…,mp},计算Hi=gbai,并计算W0=gasgk,W1=gs,构造密文: CT=(W0,W1,{Hi,i∈{0,1,…,mp}}, {(Ci,Di),i∈[1,l]}) (5) SK=(S,K,L,{Kx,∀x∈S}) (6) Trap=(S,tok0,tok1,L′, {Fi,i∈{0,1,…,mp}},{K′x,x∈S}) (7) 在关键词搜索阶段,由用户而非云服务器执行陷门生成工作,在进行搜索操作时,云服务器通过双线性映射计算得到秘密值Eroot,计算过程如下所示: (8) 如果用户的属性集能够满足访问结构(M,ρ),那么存在一组值{ωi∈Zp}i∈I使得∑i∈Iωiλi=s,所以 Eroot=-e(g,g)bstu (9) 当用户的属性集满足数据属主访问策略后,云服务器再执行关键词搜索算法判断关键词是否存在。 e(W0,tok0)=e(gasgk,gbu)= e(g,g)asbu+kbu (10) e(W1,tok1)=e(gs,g(α-t)bu)e(g,g)asbu-stbu (11) (12) 如果陷门关键词集合包含于密文中的关键词集合,则能够还原出该随机多项式,即: (13) 因此 e(W0,tok0)= (14) 等式成立,说明关键词集合存在,则云服务器返回相应的搜索结果。 4.2.1 抵抗合谋攻击 在本文方案AECKS中,DO将秘密共享值嵌入了密文中,如果要进行关键词的比较操作,那么用户或者攻击者需要将e(g,g)buts恢复出来,假设User1是一个能成功进行搜索请求的用户,即使攻击者A的属性集合包含了User1的属性集合,但是由于在进行用户私钥构造时,不同用户所选取的随机数不同,所以无法以共谋方式通过组件的组合获得User1的私钥。攻击者A无法伪造正确陷门,因为陷门值的每个组件都是以随机大数u为指数的幂,攻击者A不能根据tok0=gbu求解得到u的值,因此AECKS在离散对数问题假设下是安全的。 4.2.2 用户密钥安全 大部分基于属性的可搜索加密方案是由云服务器进行关键词陷门生成,在这个阶段,用户密钥通常不加密就直接提交给云服务器,由云服务器进行用户权限的判断,这可能导致用户密钥泄露。本文方案陷门由搜索用户调用算法生成,避免了密钥泄露的可能性。同时在密钥生成阶段,用户私钥中的组件K、L与随机大数t相关联,在离散对数困难问题假设下,用户密钥的安全性得到了保障。 4.2.3 抵抗选择关键字攻击 定理1在q-DDH假设下,AECKS能够抵抗选择关键字攻击(CKA)。 下面采用反证法证明。 (2)询问阶段1。A询问关键词集合W′c=(w′c,1,w′c,2,…,w′c,t)的陷门,同样在生成陷门阶段,对于w′c,j∈W′c,如果攻击者A已经询问过w′c,j,则挑战者S返回相应的xc,j,如果未被询问,则S随机选取xc,j∈ZP作为H(wc,j),并将其加入B中。随后攻击者A将对关键词W′c进行密文搜索,确定关键词W′c是否存在。 (3)挑战阶段。在多次询问后,A开始挑战。A选择了2个关键词集合W0=(w0,1,w0,2,…,w0,t),W1=(w1,1,w1,2,…,w1,t)发送给S。要求A不能询问(W0W1)∪(W1W0)中任何关键词子集的陷门,然后S随机选取β∈{0,1},生成Wβ的密文后发送给A。 随后S将陷门发给A,A调用搜索算法查看Wβ是否包含W′d。 (5)猜测阶段。A输出对β的猜测β′。如果β′=β则y=gam,否则y=x。攻击者A不知道主密钥,构造的m次多项式f(x)中的系数是均匀分布的,A无法从密文以及陷门中得到关于f(x)系数或主密钥的信息。如果y=gam,则对于i∈{1,2,…,m}, 因此说明生成了正确的陷门。由于A不能询问集合(W0W1)∪(W1W0)中任何子集的陷门,在这个前提下算法要分辨β的取值,只能是A从正确陷门中得到了信息。所以,如果A分辨出了β的取值,说明S具有一定优势能够判断y=gam是否成立,这与问题假设相悖,因此A不具分辨密文的优势。 本文方案能够达到CKA安全。 证毕 □ 本节将构造的AECKS方案与现有的加密方案在不同阶段的计算量进行详细比较,在数据外包模式下,考虑到DO和DU的资源有限,存储能力与计算能力可能受限,因此要求在加解密阶段和陷门生成阶段的计算量尽量小。记P表示双线性配对运算,H表示椭圆曲线群中的纯量乘法,E表示椭圆曲线群中的指数运算,v1表示访问结构中的属性个数,v2表示搜索用户具有的属性个数,user表示具有访问权限的用户个数,ky1表示文档关键词个数,ky2表示搜索关键词个数,表1给出了本文AECKS方案与文献中其他方案的性能分析对比,包括加密阶段、陷门生成、搜索阶段的计算量以及是否实现连接搜索功能。当被搜索关键词集合包含于文档的关键词集合时能够进行连接搜索,如果搜索的关键词集合大于文档关键词集合,则不存在满足条件的搜索结果,因此ky2≤ky1。 Table 1 Performance comparison of previous schemes and AECKS scheme 通过表1可以看出,与同样基于LSSS共享矩阵的可搜索加密方案[5]相比,本文AECKS方案在加密阶段由于与v1以及ky1线性相关,效率会有一定损失,但是文档的关键词个数是有限的,ky1不会无限增大,而且本文方案实现了关键词连接搜索;在陷门生成阶段,文献[5]的方案与v2线性相关,本文方案与ky1线性相关,因此计算量的开销增加有限。与文献[13]的方案对比,AECKS同样具有连接搜索功能,文献[13]加密阶段的计算量与ky1和user线性相关,这说明随着访问用户的增加,计算量也会大大增加;本文方案在加密阶段的计算量与ky1和v1相关,由于用户的属性是确定、有限的,因此在用户增加的情况下,用户在加密阶段的计算量并不会线性增加,同样由于文档关键词的个数也是有限的,因此在陷门生成阶段,本文方案具有较高效率。在搜索阶段,文献[5]的方案仅与v2线性相关,文献[13]的方案仅与ky2线性相关,本文方案与ky1和v2线性相关,但是由于搜索操作是由云服务器执行,考虑到云服务器的计算资源充足,因此不会对用户造成资源负担。同时本文加密方案支持关键词连接搜索,当数据不断增加时,不必因为关键词域重新加密数据,因此本文方案是灵活高效的,并且在通信和计算开销方面都具有较大的优势。 本文构建了一个支持关键词连接搜索的属性加密方案AECKS。基于多项式方程实现了文档的连接搜索,缩小了搜索范围。同时用户在本地生成搜索陷门,避免了密钥直接暴露给云服务器从而造成密钥泄露的风险。采用LSSS共享矩阵实现了文件的细粒度访问控制,实现了云环境下的多用户共享,并且提高了加解密效率,节省了用户资源。最后通过严格的安全性分析证明该方案能够抵抗选择关键字攻击。
2.4 线性秘密共享LSSS策略
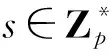
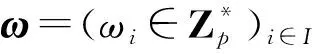
3 系统模型与方案设计
3.1 系统模型
3.2 方案定义
3.3 方案设计

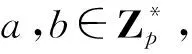
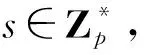
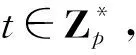
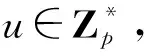
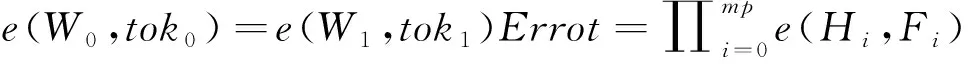
4 方案分析
4.1 正确性分析
4.2 安全性分析
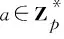
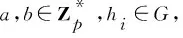

4.3 性能分析

5 结束语
