埋置空气隙柔性凸点结构随机振动应力应变分析
2021-08-06赵鲁燕潘开林
李 鹏 ,赵鲁燕 ,潘开林
(1.桂林电子科技大学 海洋工程学院,广西 北海 536000;2.桂林电子科技大学 机电工程学院,广西 桂林 541004)
当前,柔性凸点结构已逐渐成为柔性晶圆级封装CWLP(Compliant Wafer Level Package)提升电子产品性能和可靠性的核心技术之一[1]。芯片热疲劳及机械振动疲劳失效是显著影响CWLP 芯片互连结构可靠性的关键。电子产品实际服役过程中,通常会经受温度循环、外界振动等环境冲击作用,影响产品性能的同时对器件可靠性造成巨大威胁[2]。在航空航天及军事等领域,振动已成为影响电子产品可靠性的重要因素。据统计,电子设备中电路组件失效中约有20%是由振动和冲击引起的[3]。
目前,国内外学者针对不同柔性凸点结构热-机械可靠性已开展诸多研究。Fan 等[4]通过在传统晶圆级封装焊点下增加柔性聚酰亚胺层明显降低了焊点应力,提高了焊点疲劳可靠性;梁颖等[1]建立了晶圆级封装柔性凸点三维有限元模型并分析了焊点热疲劳应力应变特性;周兴金等[3]针对焊点下填充柔性层的柔性凸点进行了热-结构应力应变分析,柔性层有效降低了凸点的热-结构应力应变。
上述研究结果表明采用柔性层的柔性凸点可在一定程度上改善柔性晶圆级封装中的芯片凸点结构可靠性。笔者所在课题组前期研究表明[5],采用新型埋置空气隙柔性凸点结构可显著提升CWLP 器件热疲劳可靠性。电子产品实际工作过程中同时存在的振动或冲击也在一定程度上影响柔性凸点的结构可靠性,因此有必要进一步针对随机振动条件下的埋置空气隙柔性凸点互连结构进行互连结构可靠性分析。
本文采用设计的新型埋置空气隙柔性凸点结构,应用ANSYS 软件对柔性晶圆级封装芯片进行随机振动条件下的应力应变分析,探讨了随机振动条件下柔性凸点结构的应力应变特性及可靠性。研究结果表明,埋置空气隙的柔性凸点结构的应用能较好地满足电子产品的抗振可靠性要求。
1 有限元仿真建模
1.1 埋置空气隙柔性凸点结构
本课题组基于传统柔性芯片结构和硅微加工工艺设计的埋置空气隙柔性凸点结构如图1 所示,与相关机构合作完成的埋置空气隙柔性凸点结构原型如图2所示。

图1 埋置空气隙柔性凸点结构Fig.1 Structure of compliant bump with embedded air-gap

图2 柔性凸点实物原型Fig.2 Physical prototype of compliant bump
1.2 实体建模
采用上述柔性凸点结构,以动态随机存储器芯片为对象,依据器件结构建立单焊点三维有限元模型。整体结构由硅芯片、埋置空气隙、钝化层、铜互连结构层、凸点下金属层、焊点、焊盘、阻焊膜及PCB 基板等构成,结构模型尺寸参数如表1 所示。

表1 柔性凸点结构参数Tab.1 Structure parameters of compliant bump
仿真分析时,为确保模型精度,首先采用Surface软件模拟焊点外形尺寸参数以减小形态建模引起的误差。为减小计算规模,提升分析效率,忽略封装结构中通孔等微细结构。在不影响分析结果的前提下,为简化求解,对建模过程进行如下假设[6]:(1)芯片内部完全接触,材料连接理想,结构致密,无结构缺陷;(2)芯片制造过程中无累积残余应力和应变;(3)随机振动分析时整体结构温度保持一致。
结合芯片结构特点,采用自上而下建模步骤:先定义体,同时产生线、面,随后进行布尔操作[7],完成的柔性凸点结构模型如图3 所示。

图3 柔性凸点结构实体模型Fig.3 Entity model of compliant bump
焊料选用Sn96.5Ag3.5 无铅焊料,定义为粘塑性,焊点网格选择Visco107 单元。该单元由8 个节点定义,每个节点具有X、Y、Z方向3 个自由度。其他结构采用Solid226 网格单元,该单元由20 个节点组成,各节点有5 个自由度,用于分析大挠度和应力刚化作用[8]。
定义材料属性时假设封装结构各组成材料为各向同性、均质材料,Sn96.5Ag3.5 焊料合金弹性性能参数如表2 所示[5],其中,t为材料性能参数持续时间。焊料合金粘塑性本构方程材料参数如表3 所示[5]。为有效描述随机振动载荷条件下铜互连线应力应变特征,定义铜材料为弹塑性强化材料,采用双线性强化模型来表征[9]。其余材料定义为弹性材料,材料性能参数如表4 所示[5]。

表2 材料性能参数[5]Tab.2 Material property parameters[5]
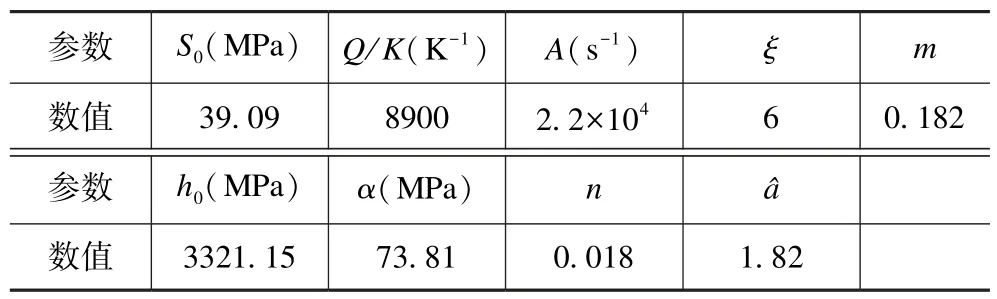
表3 Sn96.5Ag3.5 粘塑性本构材料参数[5]Tab.3 Anand model constants of Sn96.5Ag3.5[5]

表4 封装结构材料参数[5]Tab.4 Material parameters of package structure[5]
1.3 网格划分
ANSYS 提供三种网格划分方法:自由网格、映射网格和扫掠网格。为保证计算精度,网格划分不采用均匀网格且尽可能减少网格单元数目。基于此,重点研究区域及附近网格划分较密集,远离区域则网格划分较为稀疏[8]。
网格划分时,利用布尔操作及扫掠划分,为获得均匀六面体网格,首先对单焊点结构模型采用控制单元尺寸方法生成扫掠网格;然后通过拉伸操作等生成整体模型,最后依次合并节点、关键点、线和面[10]。非核心研究区域采用自由网格划分,划分所得有限元模型如图4 所示。

图4 柔性凸点结构有限元模型Fig.4 Finite element model of compliant bump
2 随机振动有限元仿真分析
随机振动问题分析时,需应用随机过程理论在激励、响应和系统特性三个要素间进行求解。进行随机响应分析前必须得到以系统频率为主的系统特性,通常需两个步骤:频率分析和随机响应分析[7]。利用ANSYS 软件进行随机振动仿真分析时,首先要对模型进行模态分析获得相关结构固有频率,然后进行PSD频谱分析[11]。本文选用Block Lanzcos 法[12]对振动模态进行提取,分析所得柔性凸点结构的前十阶固有频率如表5 所示。
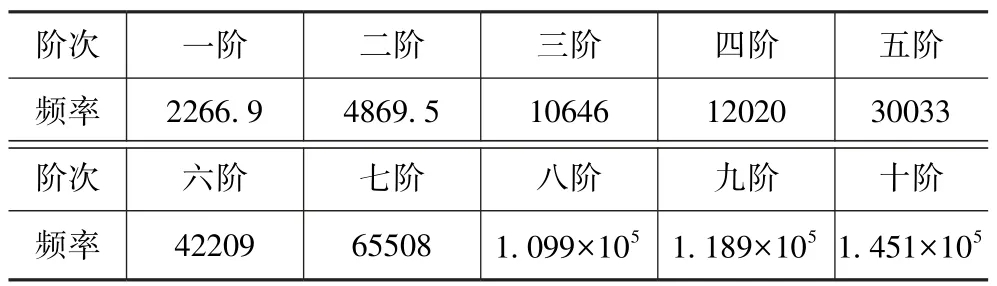
表5 前十阶固有频率Tab.5 Top ten-order natural frequency Hz
军用电子产品激励频率通常为5~2000 Hz[13]。柔性凸点结构第一阶频率是2266.9 Hz,高于军用电子产品的激励频率,柔性凸点结构能满足军用电子产品对动力学的设计要求。
2.1 载荷条件设置
设置随机振动载荷环境条件进行有限元分析时,将实际载荷情况简化为稳定温度作用外加随机振动状态进行模拟分析。随机振动基本特征是不可重复性和不可预测性,但并非是毫无规律。随机振动可通过功率频谱密度函数来反映随机振动激励输入特征,分析时需要在点集上指定功率谱密度[6]。
封装结构有限元随机振动分析包含频率分析和随机响应分析,本文按照国家军用标准军用设备环境实验方法振动试验[9]中的第8 类振动环境试验条件进行载荷设定,随机振动频率范围选择20~2000 Hz,重力加速度为9.81 m/s2。
仿真分析选择的功率谱密度为军用设备环境试验方法振动试验[9]中第8 类随机振动环境-喷气式飞机振动环境加速度PSD 谱。分析时需要在点集上指定功率谱密度,功率谱密度有位移功率、速度功率、加速度功率等谱密度形式。本文对模型施加的加速度响应值,如表6 所示。

表6 频率加速度响应值[9]Tab.6 Frequency acceleration response value[9]
2.2 边界条件设置
边界约束条件对振动分析最大应力、应变有较大影响,合理设置约束条件是仿真运算收敛的前提[13]。芯片一侧与PCB 基板通过焊点连接而不被固定,PCB基板一侧因被固定变形受到一定限制,假定PCB 基板一侧固定在刚性基体上,随机振动过程中对PCB 基板四个角点施加基础激励[14]。假设硅芯片上表面为自由面,芯片和基板两个内侧对称面上施加对称约束边界条件。此外,随机振动分析采用的基础激励只施加在模态分析中有约束处的节点。
3 仿真结果及分析
分别针对X、Y、Z三个方向施加激励进行随机振动分析,利用通用后处理器POST1 观察有限元模型的1δ解,获得各向加载应力、变形云图。从中可直观得出柔性凸点结构在受到一定范围频率内随机振动激励作用时结构变形及应力应变分布情况[15]。
3.1 X 方向施加激励
施加X方向随机振动激励时的整体结构、铜互连线和焊点等效应力、应变云图如图5 所示。由图5 可知,随机振动条件下,封装结构整体最大等效应力出现在距离芯片中心最远的边缘位置处。
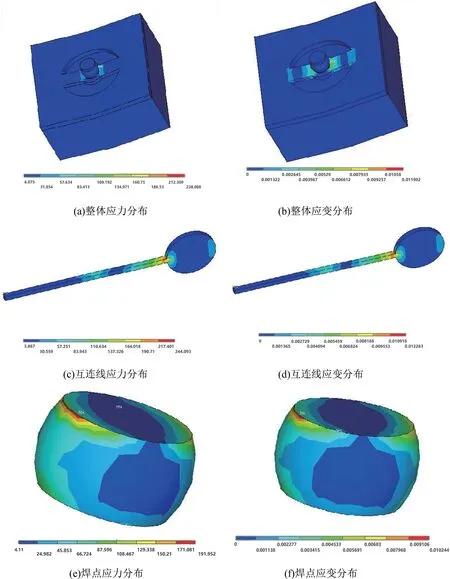
图5 施加X 方向随机振动激励时整体结构、铜互连线和焊点的等效应力、应变云图Fig.5 Equivalent stress and strain cloud diagrams of the overall structure,copper interconnets and solder joints when the X-direction random vibration excitation is applied
整体1δ应力最大值出现在焊点与凸点下金属层Ni接触面上,最大值为0.701197 MPa。互连线应力最大值出现在靠近铜焊盘连接处,最大应力值2.3 MPa;焊点应力最大值出现在与PCB 接触的铜焊盘上,最大应力值0.090519 MPa。整体结构、互连线、焊点的应变最大值与应力最大值出现位置一致,应变最大值分别为0.119×10-3,0.226×10-4和0.453×10-5。综上,X方向激励下柔性凸点结构应力应变均处于材料弹性变形范围内,结构是可靠的。
3.2 Y 方向施加激励
施加Y方向随机振动激励时的整体结构、铜互连线和焊点等效应力、应变云图如图6 所示。由图6 可知,随机振动作用下整体结构应力应变分布情况较之X向激励有所变化。施加Y方向激励时芯片1δ应力最大值出现在凸点下金属层上,最大应力为1.1 MPa;铜互连线最大应力值出现在靠近铜焊盘连接处,且互连线发生了扭曲,应力最大值为3.1 MPa;焊点应力最大值出现在焊点与PCB 的铜焊盘相接触的面上,最大值为0.110045 MPa。

图6 施加Y 方向随机振动激励时整体结构、铜互连线和焊点的等效应力、应变云图Fig.6 Equivalent stress and strain cloud diagrams of the overall structure,copper interconnets and solder joints when the Y-direction random vibration excitation is applied
Y方向激励时,芯片最大应变值出现在互连线桥体两端,最大值为0.249×10-3,究其原因,加载过程中桥体两端产生了结构突变。互连线与焊点最大应变值和最大应力值的位置是一样的,最大应变值分别为0.323×10-4和0.525×10-5。综上,Y方向激励下柔性凸点结构的各个部分也均处于弹性变形范围内,结构也是可靠的。
3.3 Z 方向施加激励
施加Z方向随机振动激励时的整体结构、铜互连线和焊点等效应力、应变云图如图7 所示。由图7 可知,芯片1δ应力最大值出现在焊点与凸点下金属层接触处,最大值为0.519149 MPa。互连桥两端应力较大,在互连桥两端出现了非圆滑过渡,结构产生突变。互连线应力分布最大位置是与铜焊盘相接触的一端,最大应力值为1.01 MPa,出现了应力集中现象。焊点应力最大位置是焊点与下部金属层相接触的圆面边缘位置,最大应力值为0.046485 MPa。

图7 施加Z 方向随机振动激励时整体结构、铜互连线和焊点的等效应力、应变云图Fig.7 Equivalent stress and strain cloud diagrams of the overall structure,copper interconnects and solder joints when the Z-direction radom vibration excitation is applied
芯片最大应变出现在凸点下金属层与PI 互连桥接触处,应变值为0.962×10-4。互连线最大应变出现在互连线靠近铜焊盘一侧,最大应变值0.104×10-4。焊点最大应变值出现在焊点与下部金属层相接触面的外圆边缘,最大应变值为0.202×10-5。综上,Z方向激励下柔性凸点结构的各个部分也未超过材料弹性变形极限,结构也是可靠的。
3.4 仿真结果分析
对比施加X、Y、Z三个方向激励条件所得仿真分析结果可知,施加Y方向激励时互连线1δ应力值显著大于X、Z方向激励情形下的应力值。施加Y方向激励时铜互连线最大应力出现在靠近铜焊盘的位置,应力值为3.1 MPa,发生概率为68.3%;介于1δ和2δ之间的应力为6.2 MPa,发生概率为27.1%;超过3δ的应力为9.3 MPa,发生概率仅为0.27%,应力值远小于铜材料屈服极限180 MPa。
综上所述,随机振动载荷对柔性凸点结构可靠性影响总体较小,埋置空气隙柔性凸点结构可提供随机振动条件下芯片三维方向上良好的柔性适应性,可避免加载频率范围内随机振动产生的互连结构失效。
4 结论
本文采用ANSYS 软件在热与振动复合载荷下对埋置空气隙柔性凸点的芯片封装结构进行了应力应变分析。由分析结果可知,柔性凸点结构一阶固有频率为2266.9 Hz,满足军用电子产品对动力学设计的要求。分别施加X、Y、Z方向激励后的随机振动仿真分析结果表明,施加Y方向激励时铜互连线最大应力出现在靠近铜焊盘的位置处,超过3δ的应力为9.3 MPa,发生概率仅为0.27%。超过3δ范围的应力远小于铜材料屈服极限应力。埋置空气隙柔性凸点结构的应用能较好地满足电子产品的抗振设计要求,提高电子产品抗振疲劳可靠性。
