基于小波分析的ARIMA-GRNN模型的新疆CPI分析

唐 萍，王丰效

(喀什大学 数学与统计学院，新疆 喀什 844000)

0 引言

居民消费价格指数(CPI)是用来反映消费者购买产品价格水平的变动情况，CPI的高低在一定程度上能够说明通货膨胀的严重程度，是政府制定相关政策和计划，进行宏观调控的理论依据[1].近年来，国家大力扶持新疆经济，新疆CPI与新疆经济发展息息相关，因此通过对该地区CPI进行分析，在一定程度上对当地政府制定经济发展策略具有重要意义.研究CPI的方法很多，如小波分析、神经网络、灰色模型、SARIMA、ARIMA、VAR等.文献[1]通过小波分析和ANIFS模型对CPI进行分析；文献[2]通过ARIMA模型对CPI进行了预测分析；文献[3]通过实例验证小波分析的BP-SARIMA预测模型的有效性；文献[4]说明了GRNN神经网络在实际应用中优于BP神经网络.基于以上研究基础，本文先根据小波分析对数据进行预处理，再利用新疆CPI相关数据建立小波ARIMA-GRNN模型进行实证分析.

1 小波分析的ARIMA-GRNN模型

1.1 小波分析

小波分析是建立在泛函分析、Fourier分析、样条分析及调和分析基础上的新的分析处理工具.它又被称为多分辨分析，在时域和频域同时具有良好的局部化特性,常被誉为信号分析的“数学显微镜”.近十多年来,小波分析的理论和方法在信号处理、语音分析、模式识别、数据压缩、图像处理、数字水印、量子物理等专业和领域得到了广泛的应用[5].将小波分析应用于时间序列中，可以将数据分出周期项、趋势项和随机性[8].小波分析主要通过分解、去噪、重构三个步骤.设时间序列数据为f(t),则f(t)的多分辨分解可以表示为

其中φj,k(t)，φJ,k(t)分别是尺度函数φ(t)和母小波函数φ(t)的伸缩和平移函数簇；cj,k为尺度展开系数；dj,k为小波展开系数；J为任意设定的尺度.

1.2 ARIMA模型

自回归求和移动平均模型(Autoregressive Integrated Moving Average)[2]，简记为ARIMA(p,d,q),模型结构如下：

1.3 GRNN神经网络

广义回归神经网络(GRNN)是RBF神经网络的一种改进.GRNN在结构上主要由四层构成，如图1所示，分别为输入层(input layer)、模式层(pattern layer)、求和层(summation layer)和输出层(output layer).对应网络输入

X=(x1,x2,…,xn)T

和网络输出

Y=(y1,y2,…,yk)T.

相对于BP神经网络来说,GRNN的非线性映射能力和学习速度非常强,且仅只含唯一参数光滑因子，网络学习训练全部依据样本数据，可以最大程度上防止人为主观因素的影响，大大提高预测的精度.

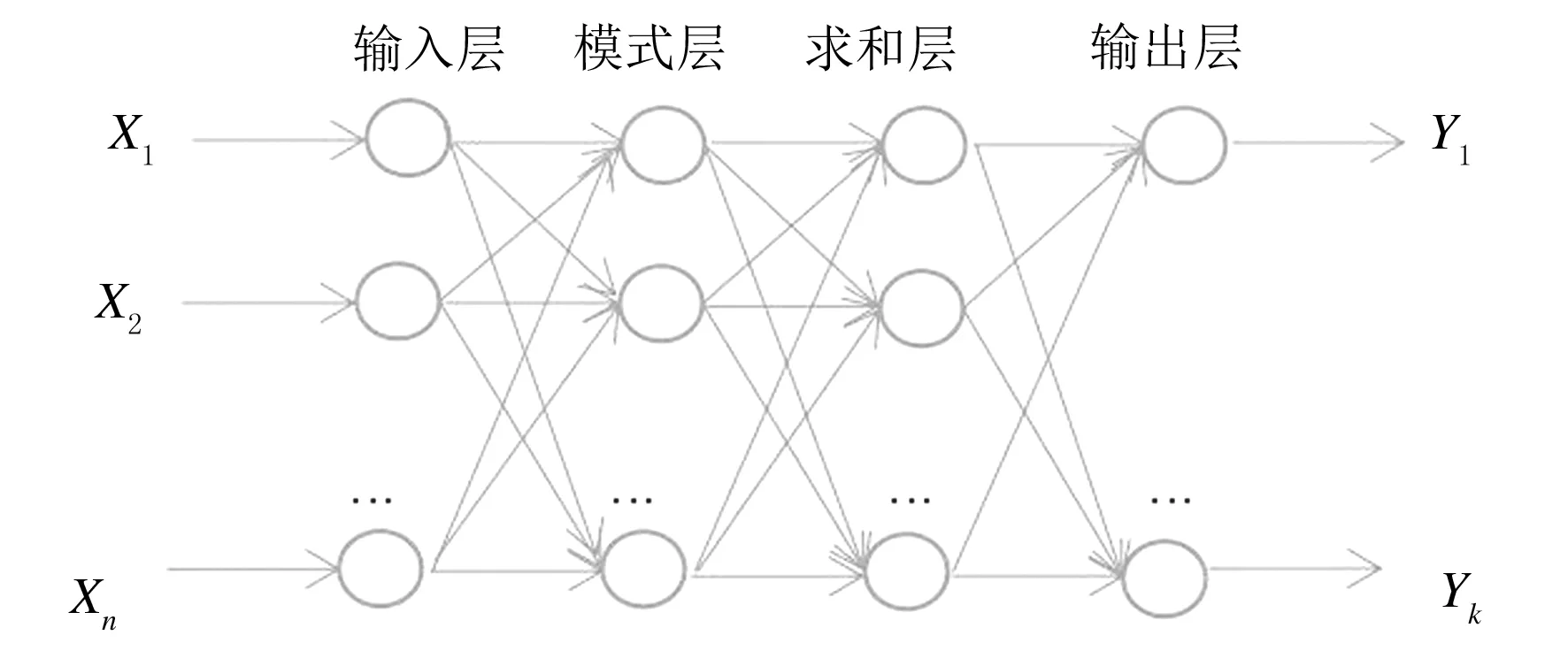
图1 GRNN神经网络结构图

输入层的神经元的个数等于输入样本向量的维数.将变量输送给模式层，模式层的神经元个数为样本的个数，传递函数为

输出变量i和对应样本X之间Euclid距离为

求和层的计算公式有两种，一种是

权值为1，传递函数为

另一类计算公式为

传递函数为

1.4 小波分析的ARIMA-GRNN模型的构建

首先对原始数据进行小波分解预处理，再对预处理后的数据做ARIMA模型预测，最后通过GRNN模型进行预测修正.通过结合小波分析、ARIMA和GRNN神经网络模型的优点，建立小波分析的ARIMA-GRNN模型.小波分析的ARIMA-GRNN模型的建模步骤为：

步骤1 选择合适的小波函数及分解层数对原始数据进行分解.

步骤2 分别对近似部分aj=(xj,1,xj,2,…,xj,n)和细节部分dJ=(yj,1,yj,2,…,yj,n)建立合适的ARIMA模型，1≤j≤J，J为分解的层数.

1.5 模型预测的评价标准

(1)均方根误差RMSE准则

其中:yi代表预测值;gi代表真实值.RMSE值越小，代表模型的预测准确度越高.

(2)平均绝对误差MAE准则

其中:yi代表预测值;gi代表真实值;MAE值越小，代表模型的预测准确度越高.

(3)Theil不相等系数准则

其中:U的取值范围为0到1之间，当U的取值越接近于1时，代表预测值跟真实值相差很大，即模型的预测准确度越低；当U取值越趋于零时，代表预测值接近于真实值，即模型的预测准确度越高.

2 实证分析

首先对CPI数据进行数据特征分析，然后分别建立ARIMA、小波ARIMA和小波ARIMA-GRNN预测模型，通过比较3个模型的预测精度，来验证小波ARIMA-GRNN是否具有一定的优势.

本文选取新疆维吾尔族自治区2000年1月至2021年2月的CPI月度数据，数据共计254个，数据来源于国家统计局.研究中模型估计和预测利用了Eviews和Matlab软件工具完成.

2.1 小波分解及去噪

CPI月度数据不可避免地受到随机扰动项的干扰，收集到的数据会包含一定的噪声，这些噪声与数据的本质特征无关，但是会对预测结果形成一定的干扰.为了提高预测的精度，对CPI原始数据进行小波处理.

目前小波函数的选择并没有统一的理论标准，根据本文研究的CPI数据的特征，选取db4小波作为小波基[5]，对CPI进行一层小波分解得到各尺度的近似分量和细节分量，如图2所示.其中s代表的是CPI数据的原始图像，d代表细节分量，下标代表分解的层数，a代表近似分量.

S=a1+d1.

以上小波分解过程通过MATLAB小波分析工具箱完成.

图2 小波分解

2.2 基于小波分析的ARIMA模型建模

对近似分量a1和细节分量d1分别用经典的时间序列进行相应的拟合和预测.近似分量a1的时序图如图3所示，由该时序图可知该序列为非平稳时间序列，对a1序列进行ADF检验，检验结果如表1所列，ADF检验未通过，该序列为非平稳时间序列.

对数据进行差分处理，首先对序列进行一阶差分处理，一阶差分后的ADF检验结果如表2所列，由表2可知一阶差分后的a1序列为平稳序列，因此，模型参数d的取值为1.

通过差分序列的相关图，自相关系数和偏自相关系数确定参数p,q的值.自相关图(ACF)和

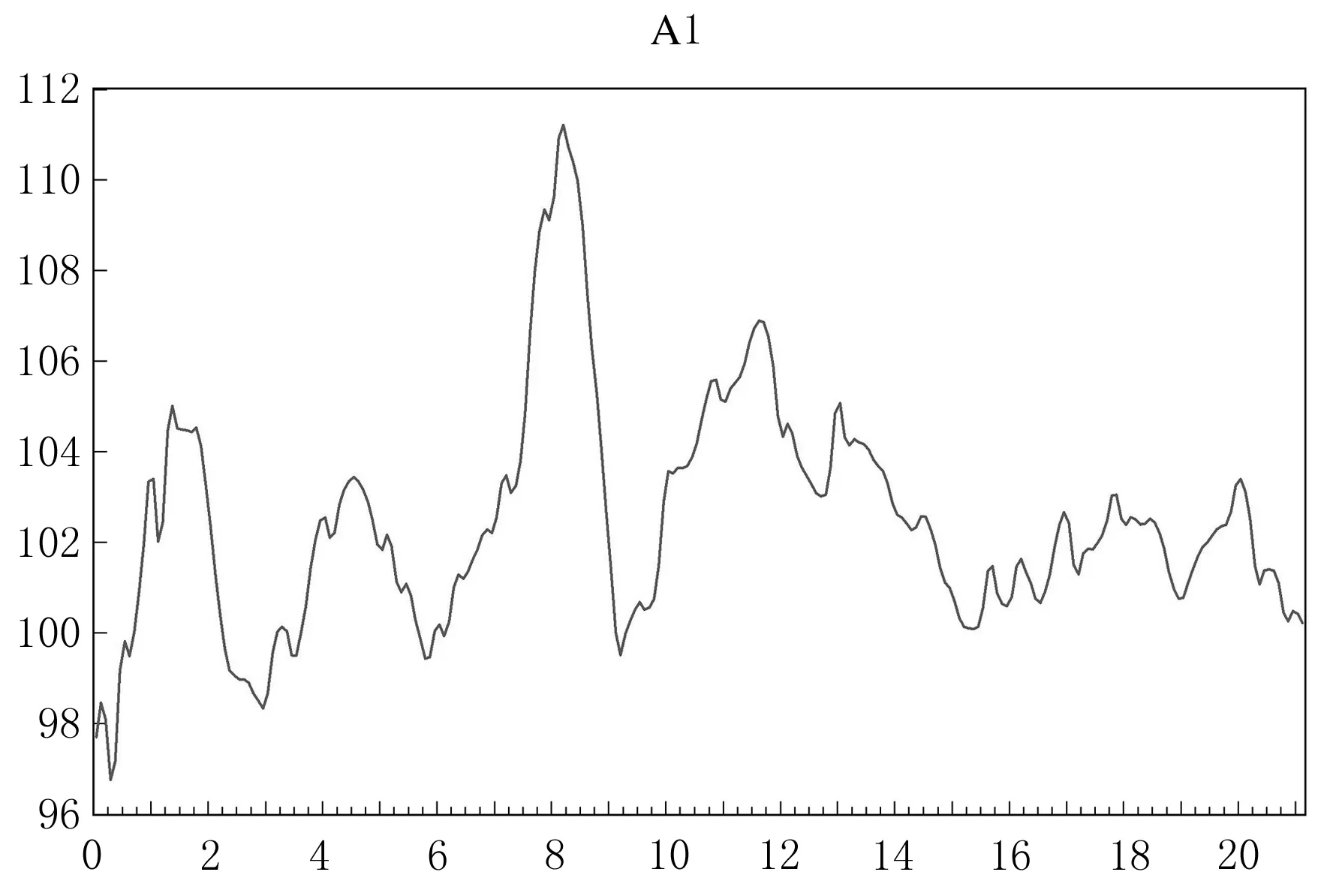
图3 a1时序图

偏相关图(PACF)如图4所示，根据赤池信息准则(Akaike Information Criterion,AIC)和施瓦茨准则(Schwarz Criterion,SC)较小，结合拟合度(R-squared)最优原则，最终确定最优模型为ARIMA(1,1,1)，a1的ARIMA(1，1，1)模型的拟合结果如图5所示，参数显著性皆为显著，且该模型通过有效性检验，利用其进行预测，得出a1的ARIMA预测模型为

a1=(x1,1,x1,2,…,x1,p).

表1 a1序列的ADF检验结果

表2 a1序列一阶差分后ADF检验结果

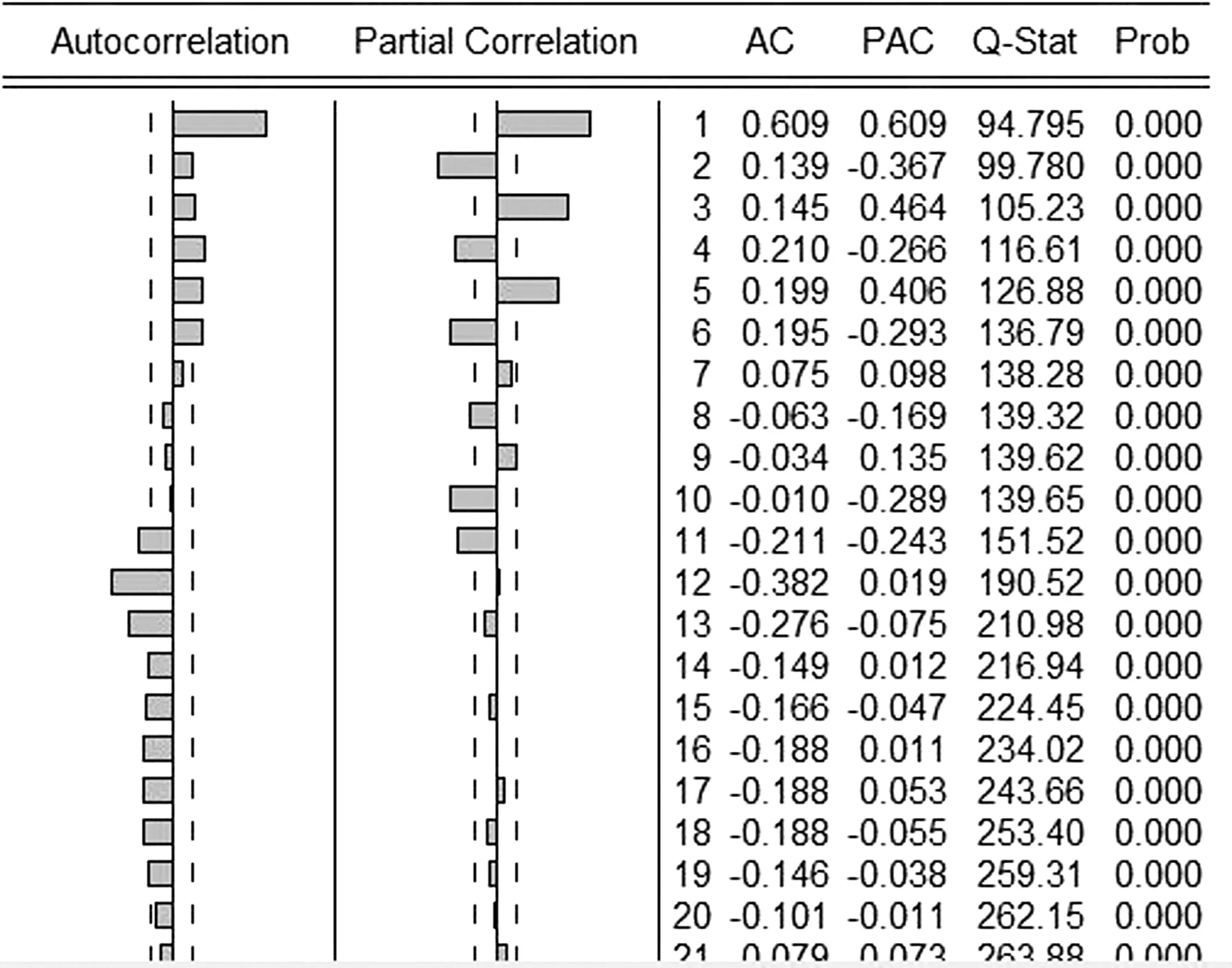
图4 a1一阶差分后的ACF和PACF图

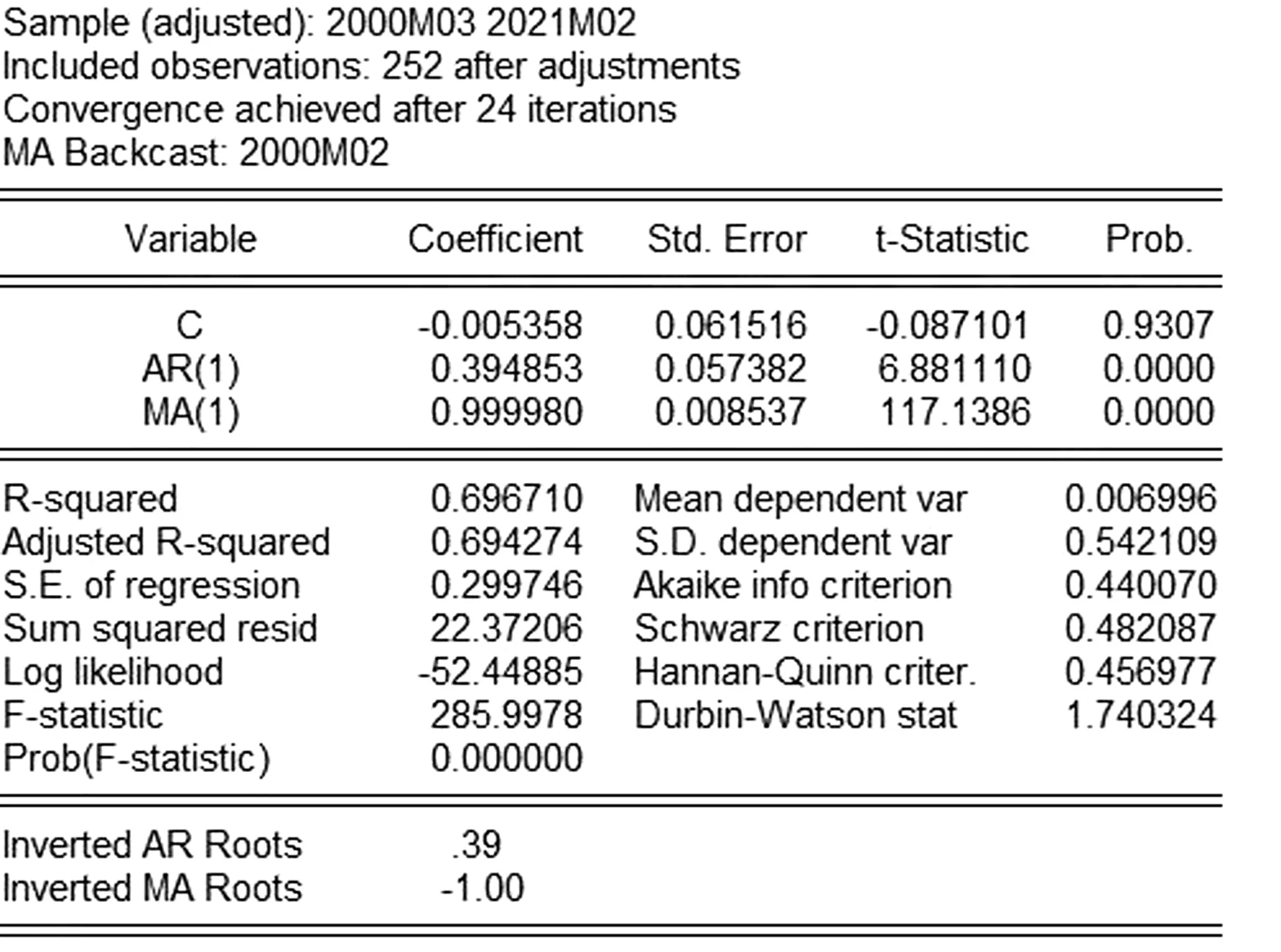
图5 a1的模型拟合图

同样最终确定b1最优模型为ARMA(2,1)，参数显著性皆为显著，且通过有效性检验，利用其进行预测得出d1的ARMA预测模型为

d1=(y2,1,y2,2,…,y2,q).

2.3 基于小波分析的ARIMA-GRNN模型建模

将a1的预测模型和d1的预测模型W=(W1,W2)作为GRNN神经网络的输入变量，将CPI数据的真实值作为输出变量，总共有252个数组，前248个数组作为训练集，后4组作为网络的预测数据.通过交叉验证，确定最优的spread值.

通过程序运行，得出最佳spread值为0.1，最终得出模型的预测值，如图6所示.

图6 GRNN在MATLAB中运行结果图

2.4 模型的比较评价

为了比较小波分析及未经小波分析的预测效果的差别，建立ARIMA模型[2]、小波ARIMA模型.将ARIMA模型、小波ARIMA模型和小波ARIMA-GRNN 模型的预测结果进行比较.各模型的预测值跟真实值的误差见表3.

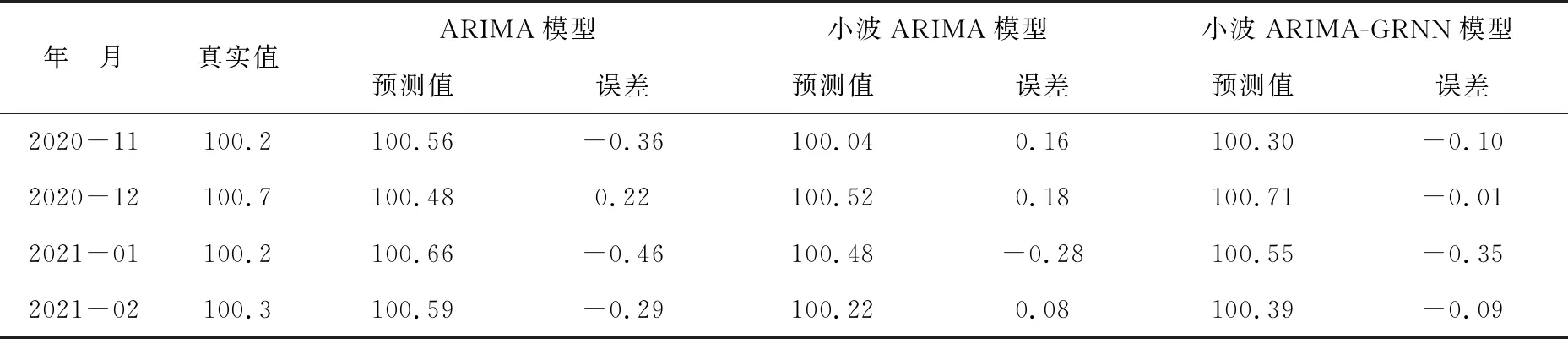
表3 各预测模型的相对误差表

由3种模型的预测结果的误差比较可知，小波ARIMA-GRNN模型的误差要比小波ARIMA模型小，小波ARIMA模型的误差要比小波ARIMA模型小.

进一步根据均方根误差准则、平均绝对误差准则和Theil不相等系数准则来比较这3种模型的预测效果，结果见表4所列.

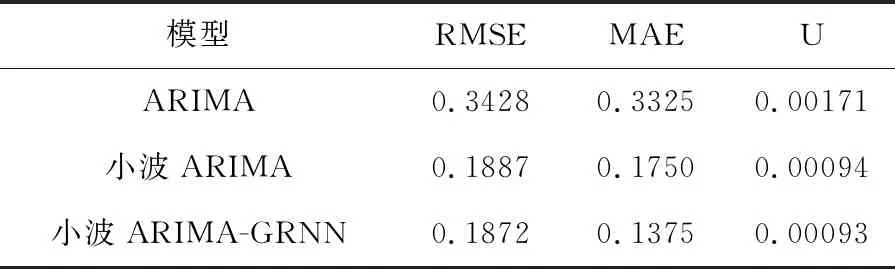
表4 各模型指标评价结果

RMSE和MAE的值越小，模型的效果越好.U值越接近于零，模型预测的准确度也就越高.通过实证分析表明将小波分析应用到时间序列中，能显著地提高模型的预测精度.小波ARIMA和小波ARIMA-GRNN模型的预测精度要比ARIMA模型的高.通过GRNN神经网络的预测修正，其预测精度要比小波GRNN高.小波ARIMA-GRNN模型优于小波ARIMA模型，优于ARIMA模型.

3 结语

本文针对CPI数据的特点，建立小波ARIMA-GRNN模型.对于该模型，小波分析能够将波动的CPI序列进行去噪分解，得到不同频率的近似分量和细节分量，对于不同的近似分量和细节分量其数据特征也不一样，能够为后续的时间序列建模提高预测精度.进一步的研究方向：①模型的改进.比如说将ARIMA模型换成其他的模型，或者将GRNN神经网络换成其他类型的神经网络，或者选取其他的小波基，预测精度是否提高.②模型的适用性.模型是否适应于其他的经济数据预测.