典型区域土壤重金属空间变异与多变量均质性分区研究

杨楠，连雅，，夏新，张明顺，李宗超*

（1.中国环境监测总站，北京 100012；2.北京建筑大学环境与能源工程学院，北京 100044）

土壤形成过程中受到母质、地形、水文和农业生产等自然因素和人类活动因素影响，在空间和时间尺度上均具有高度的异质性[1]。在土壤污染调查中，为提高调查结果的精度，常加密布设点位[2]。但在后续跟踪监测中难以对全部点位开展长期监测，因此需对地块内的调查点位进行筛选。WANG 等[3]、GAO 等[4]研究中和《地理信息 空间抽样与统计推断》（GB/Z 33451—2016）标准中提及可在均质性区域内筛选代表性点位。为获得土壤重金属均质性区域，本文开展了相关分区方法研究，使地块分区后子区域内土壤重金属含量趋于均质化，子区域间趋于异质化。

目前多数学者使用地统计学与GIS 结合的方法对土壤重金属空间变异特征进行研究，利用半变异函数描述土壤重金属空间变异结构，使用基于半变异函数的克里金插值对污染空间进行预测，直观地观测重金属的空间连续分布情况[5−9]。模糊聚类分区方法可同时考虑多个土壤属性变量，进行土壤空间管理区域的划分[10−13]，但该方法未考虑变量之间的相关性对聚类分析带来的误差影响[14]。主成分−模糊聚类分析方法，利用主成分分析提取原始数据的绝大部分信息并将多个具有相关性的指标转化为少量互不相关的综合性指标，再将主成分得分作为新指标进行聚类分析，极大提高了分区的效率和准确性，该方法目前被广泛应用在基于有机质等土壤养分指标的土壤空间均质性分区研究中[15−17]，但将其应用于以重金属含量为指标的土壤污染空间均质性分区研究相对较少。

本研究以土壤重金属均质性分区为导向，利用地统计学与GIS 结合的方法对土壤重金属元素的空间变异结构特征进行描述，获得重金属空间插值结果；利用主成分−模糊聚类分析方法开展重金属空间均质性分区研究；通过方差分析验证分区结果合理性，并通过与重金属空间插值结果比较，讨论分区结果可靠性。本研究旨在证明主成分−模糊聚类分析方法可用于重金属均质性分区，并为在均质性区域内筛选代表性点位奠定基础。

1 材料与方法

1.1 研究区域概况

为充分研究主成分−模糊聚类分析分区方法的适用性，本文选择了受自然和人为因素影响、土壤重金属空间变异特征较复杂的某山区金属矿下游的耕地地块作为研究区域。该区域位于北回归线以北，平均海拔为805 m，区域面积为5.54 km2，东西横跨2 km，南北纵跨4 km。研究区域土壤由两种成土母质——泥盆系碎屑岩和泥盆系碳酸盐岩发育而来，区域范围内土壤类型有红壤和水稻土两种，所占面积分别为3.62 km2和1.92 km2。

1.2 数据来源

将研究区域划分为200 m×200 m 的网格，并在耕地内布设样点（112 个），如图1 所示。通过GPS 开展野外定点采样工作，采用单点采样法，采样深度为0～20 cm。采样过程中避免与金属工具接触，样品置于聚乙烯塑料袋中。土壤样品经风干、逐级研磨过100目筛后，开展8种重金属检测。采用盐酸−硝酸−氢氟酸−高氯酸全消解的方法，Pb 和Cd 含量采用石墨炉原子吸收光谱法（GB 17141—1997）测定，Cr、Zn、Cu和Ni含量采用火焰原子吸收法（HJ 491—2009）测定，As 和Hg 含量采用原子荧光光谱法（GB 22105.1—2008和GB 22105.2—2008）测定。分析过程中均加入国家土壤标准物质（GSS−6），重金属回收率均在90%以上，所有样品均设置3 个平行样，平行样的相对误差小于10%，同时进行空白实验，选10%的样品做重复测试，相对误差在±5%以内。

1.3 研究方法

1.3.1 土壤重金属含量地统计分析

基于地统计学对土壤重金属含量的空间结构特征进行探索性分析，包括空间自相关性分析和空间变异性分析。

半变异函数是地统计学函数，一般用来描述区域化变量的空间变异结构[18]。数学计算公式为：

式中：N（h）为具有相同间隔距离h时的样点对数量，Z（xi）和Z（xi+h）分别为位置在xi和xi+h上的变量实测值。半变异函数有4 个重要的参数：块金、基台值、块金效应和变程。块金值代表随机变异。基台值代表由结构变异和随机变异组成的总体变异。块金效应是块金值与基台值的比值，即随机（人为）因素引起的空间变异占总体变异的比例，取值分别为：0%～25%、25%～50%、50%～75%、75%～100%时，代表的空间相关性程度分别为：强、明显、中等、弱[19]。变程表示空间自相关的作用范围，在变程范围内，变量具有空间自相关性，反之则不存在[20]。

克里金插值法是以变异函数理论和结构分析为基础，对区域化变量进行无偏最优估计的插值方法。计算公式为：

式中：x0为待预测样点，Z（xi）为样点xi处重金属的测试值，λi为样点xi处测试值的权重。

1.3.2 主成分−模糊聚类分析

主成分分析可以通过正交变换将多个相关性变量转化为几个互不相关的综合变量（主成分），一般提取特征值>1 的主成分进入后续数据分析与研究[21−22]。样点主成分值（即主成分得分）的计算公式为：

式中：Fnj为第n个样点第j项主成分的取值；m为常数，表示原始变量的个数；eji为第j项主成分第i项变量的载荷；fj为第j项主成分的特征值；Xni为第n个土壤样点第i项变量的标准化值。

模糊聚类分析是根据样本数据本身所具有的特征，采用相似性原则进行分类，最终使同类分区内数据变异最小，而不同类分区间数据变异最大[23]。分类效果的优劣主要由两个指标[模糊效果指数（Fuzzy performancel index，FPI）和归一化分类熵（Normalized classification entropy，NCE）]确定，计算公式分别为：

式中：c为分类数，n为样本数，uik为第k个样本属于第i个聚类中心的模糊隶属度。FPI和NCE取值均为0～1，FPI越接近0，聚类所得分区之间共用的数据越少，聚类效果就越好。NCE越接近0，分区内的数据相似程度越高，聚类效果就越好。因此，FPI和NCE同时取最小值的聚类数为最佳分区数[24]。

1.3.3 数据分析和软件制图

使用SPSS 24.0 软件进行描述性统计分析和主成分分析，使用GS+9.0 软件进行半方差函数拟合，使用ArcGIS 10.2 软件绘制重金属含量空间分布预测图和主成分得分空间分布预测图，使用MZA 1.0.1 软件进行模糊聚类分析，通过ArcGIS 10.2 软件绘制分区结果图。

2 结果与分析

2.1 土壤重金属含量状况

由柯尔莫戈洛夫−斯米诺夫（Kolmogorov−Smirnov）正态分布检验（P≤0.05）结果可知，Cr、Ni 含量符合正态分布，Cu对数变换后符合正态分布，Hg倒数变换后符合正态分布，As、Pb、Zn、Cd不符合正态分布。研究区域土壤重金属含量统计情况见表1，由表1 可知，As、Cr、Pb、Zn、Cd、Cu、Ni、Hg 峰度均大于0，说明其数据分布曲线较为陡峭，为高狭峰。Cr 元素数据分布具有负偏性，说明Cr 元素含量中有偏低值；其余7 种元素数据分布具有正偏性，说明该7 种元素含量中均有偏高值，尤其除Ni 外，其他6 种元素偏度较高，说明其偏高的测试值较大。8 种重金属变异程度由强到弱为：As>Pb>Zn>Cd>Hg>Cu>Ni>Cr，变异系数取值0%～10%为轻度变异，10%～100%为中度变异，大于100%为高度变异[25]，因此，Hg、Cu、Ni、Cr 为中度变异，As、Pb、Zn、Cd为高度变异。

表1 土壤重金属含量统计特征描述Table 1 Description of statistical characteristics of heavy metal contents in soil

2.2 土壤重金属含量地统计分析

2.2.1 土壤重金属空间变异分析

地统计学一般要求所研究的区域化变量均服从正态或近似于正态分布[26]。本研究根据拉依达准则将样本平均值加减3 倍标准差区间外的数据定为异常值，以平均值与3 倍标准差的和或差代替异常值[27]。对异常值处理后的各重金属变量数据再次进行柯尔莫戈洛夫−斯米诺夫正态分布检验，Cr、Cu、Ni、Hg 4 个变量的数据符合正态分布，As、Pb、Zn、Cd 4 个变量的数据在进行对数变换后近似符合正态分布，均符合要求。

对研究区域As、Cr、Pb、Zn、Cd、Cu、Ni、Hg 8 种重金属开展空间变异分析，对各重金属数据构建半变异函数模型，选择决定系数较高且残差最小的拟合模型作为最优模型，模拟结果见表2。从拟合结果来看，8 种元素的决定系数均高于0.8，说明各变量的模型拟合精度较好，满足后续分析要求。Zn、Cd元素的块金效应低于25%，说明其具有强烈的空间自相关性；As、Cr、Pb、Cu、Ni、Hg 元素的块金效应为25%～75%，说明其具有中等程度的空间自相关性。

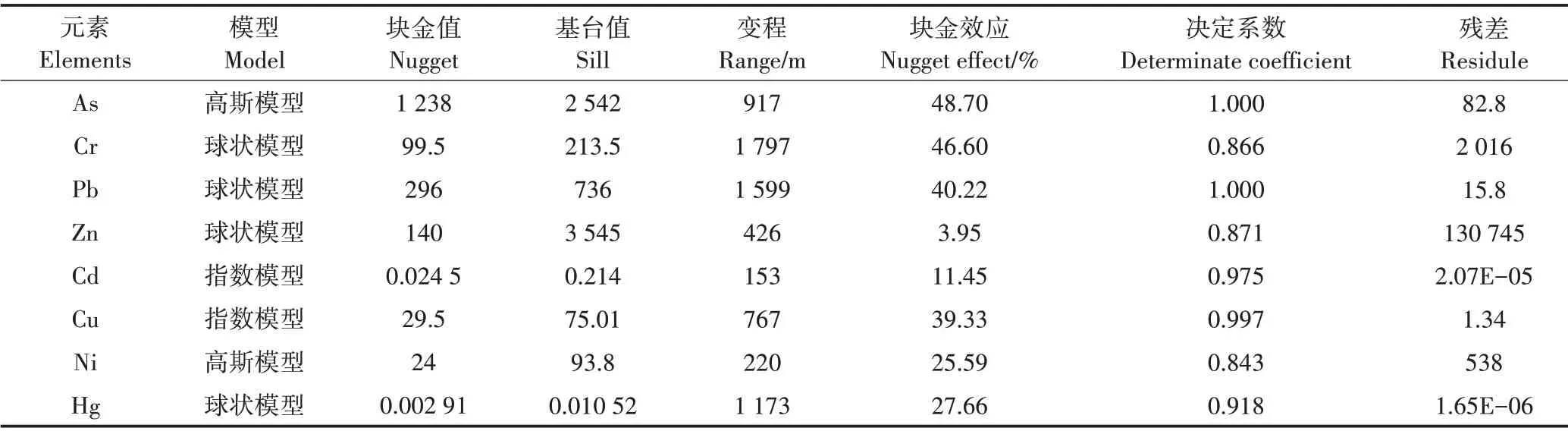
表2 土壤重金属变量半变异函数拟合及相关参数Table 2 Semivariogram fitting and related parameters of heavy metal variables in soil

8 种重金属变程从大到小为：Cr>Pb>Hg>As>Cu>Zn>Ni>Cd，自相关范围逐渐减小，除Cd 外（其有效变程为153 m），其余7种重金属的变程均大于布设点位的影响范围（200 m），说明土壤样点基本在各金属元素的空间自相关范围内，各元素的半变异函数模型能反应研究区域内重金属含量的空间变异情况。

2.2.2 土壤重金属含量空间分布特征

根据各元素分布特征对数据进行相应的对数变换，根据趋势分析结果剔除相应的全局趋势，根据上述最佳半变异函数模型及其拟合参数，确定相应的插值参数，对8 种重金属含量进行普通克里金插值，利用均方根误差、标准均方根误差和平均标准误差作为指标，通过交叉验证评估克里金插值模型的精度，确定最优插值精度的插值模型，最终获得各重金属元素含量的空间分布预测图，见图2。

由图2 可知，As、Pb、Zn、Cd、Cu、Hg 6 种重金属含量的空间分布在整体上具有一定的相似性，大面积高值区在西部靠北区域，向东重金属含量逐渐减小；Cr元素含量空间分布则与之相反，高值区在东部靠北区域，向西重金属含量逐渐减小；而Ni 元素含量空间分布则无明显的大范围高值区域，只在西部靠北区域有小面积高值区。

2.3 土壤重金属多变量均质性分区研究

2.3.1 重金属变量相关性分析

为使均质性分区更符合研究区域实际重金属含量分布情况，以重金属含量原始测试值为数据源，进行主成分−模糊聚类分析和相关的分区结果讨论。主成分分析前对指标间相关性进行分析，形成相关系数矩阵，见表3。8种重金属中，除Ni与As、Cr、Pb之间相关系数未达显著水平，其他指标间的相关性均达显著水平（P<0.01），其中Cd 与Zn 的相关系数最大，达到0.989。Bartlett 球状检验显示Bartlett 值=1 319.933，P<0.05，指标间存在相关性，适合进行主成分分析；KMO检验显示KMO值=0.784（>0.5），主成分分析的结果可接受。

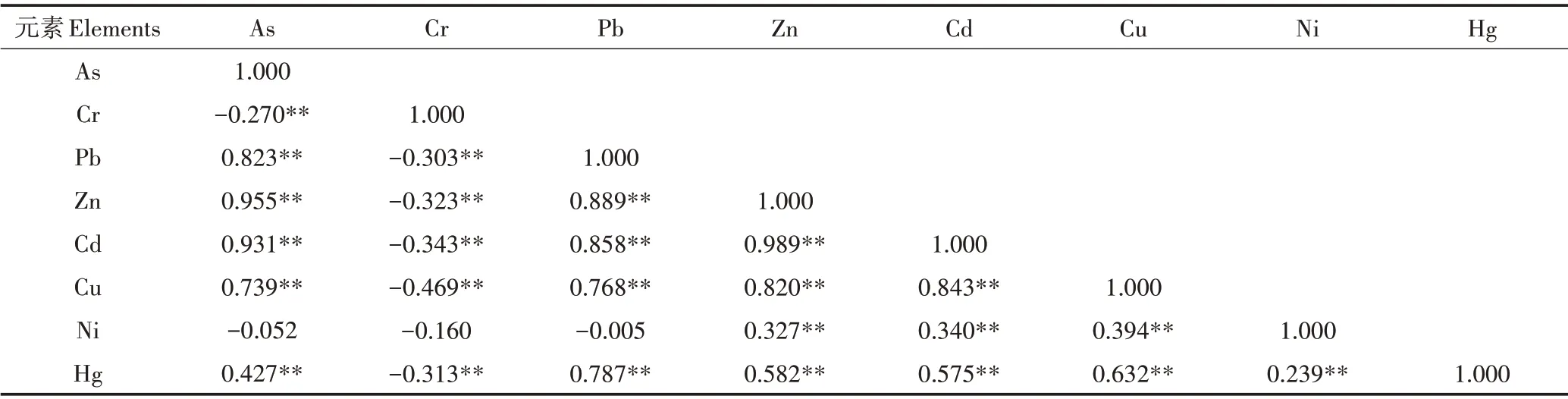
表3 土壤重金属变量相关系数矩阵Table 3 Correlation matrix of heavy metal variables in soil

2.3.2 主成分分析

对8种重金属变量进行主成分分析，结果见表4。采用最大方差旋转法可提取出3 个主成分——第一主成分（PC1）、第二主成分（PC2）和第三主成分（PC3），作为模糊聚类分析的3个指标，旋转后其特征值分别为4.65（>1）、1.28（>1）和1.17（>1），方差贡献率分别为58.13%、15.96%和14.62%，累计贡献率为88.71%，即这3 个主成分涵盖了原始数据信息总量的88.71%。根据公式（3）和表4中各成分载荷，计算112个样点的第一、第二和第三主成分得分，在比较普通克里金法与反距离权重法交叉验证精度后，选择使用精度较高的普通克里金插值法对其进行插值，结果见图3。

由表4 可知，第一主成分中，As、Pb、Zn、Cd、Cu、Hg 元素载荷较高，说明第一主成分主要反映了该区域As、Pb、Zn、Cd、Cu、Hg 的分布状况，即第一主成分得分的空间分布与As、Pb、Zn、Cd、Cu、Hg 含量的空间分布呈现高度正相关。第二主成分中，Cr 元素载荷较高，说明第二主成分主要反映了Cr 的分布状况，即第二主成分得分的空间分布与Cr 含量的空间分布呈现高度负相关。第三主成分中，Ni 元素载荷比较高，说明第三主成分主要反映了Ni 的分布状况，即第三主成分得分的空间分布与Ni 含量的空间分布呈现高度正相关。

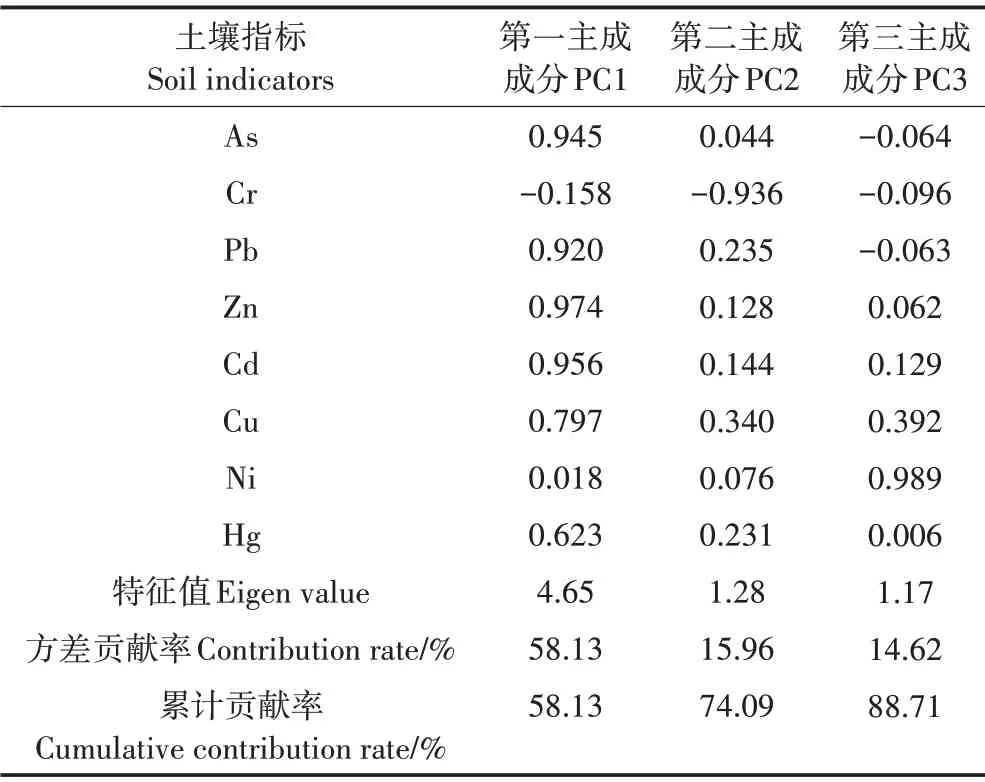
表4 土壤重金属主成分分析结果Table 4 Principal component analysis results of soil heavy metals

2.3.3 聚类分析

以30 m×30 m 为栅格像元大小，从2.3.2 第一、第二和第三主成分得分的克里金插值图中，将研究区域划分为6 184 个栅格，分别提取每个栅格PC1、PC2 和PC3 得分3 个指标的数据，进行模糊聚类分析。软件参数设置为[13，28]：最大迭代次数为300，收敛阈值为0.000 1，模糊指数为1.30，最大分区数为6，最小分区数为2，获得NCE和FPI曲线如图4 所示。由图4 可知，将研究区域分为3 个分区是最佳的。分区结果如图5所示。

2.3.4 分区结果合理性验证

如图5 所示，通过主成分−模糊聚类分析方法将研究区域分为3 个互相镶嵌的子区域：分区1、分区2和分区3，土地面积占比分别为1%、30%和69%，所含样点分别为2、33个和77个。为验证分区结果的合理性，统计3 个分区各重金属含量平均值并进行方差分析，结果见表5。方差分析结果显示，8 个重金属指标在3 个分区的均值均有显著性差异（P<0.05）。3 个分区中，As、Pb、Zn、Cd、Cu、Ni、Hg 平均含量为分区1>分区2>分区3，Cr 平均含量为分区3>分区2>分区1，与土壤重金属含量空间分布预测（图2）所显示的研究区域重金属的空间分布基本一致。为进一步验证分区结果，分别计算分区前后各重金属的变异系数并进行比较（图6），3 个分区内8 个重金属变量的变异系数，除Cr的分区1变异系数稍大于分区之前区域整体的变异系数，其他变量的分区变异系数均小于分区前整个研究区域。即分区后子区域内的变异变小，而子区域之间的重金属含量变异变大，分区合理。

表5 不同土壤重金属分区平均含量统计及方差分析Table 5 Average content statistics and variance analysis of different soil heavy metal zones

3 讨论

3 个分区互为镶嵌的碎片化小区域在重金属含量空间分布预测图（图2）中未得到全面展现，为对其进行具体讨论，对碎片化小区域内点位进行编号（图5），分区1的碎片化区域内点位为9号和12号，分区2的碎片化区域内点位为1、2、3、4、5、6号和13号，分区3的碎片化区域内点位为7、8、10号和11号，利用Anse⁃lin Local Moran′ I 指数对碎片化小区域的13 个点位的聚类及异常值情况进行分析。黑色9 号和12 号点位为As、Pb、Cd、Hg 含量影响的“高值聚类点位”，是研究区域重金属含量最高值和次高值点位。红色1、2、3、4、5、6 号和13 号点位为被As、Cd、Cu、Ni 含量影响的“被低值围绕的高值异常点位”，所以其被分为分区2。而蓝色7、8、10号和11号点位为As、Pb、Zn、Cu、Hg 含量影响的“高值聚类点位”，但是与其周围的分区1 内点位数据对比来说，属于相对低值点位，所以被分为分区3。主成分−模糊聚类分析方法得到的分区与该研究区域实际土壤重金属含量空间分布情况相符。而图2 重金属含量空间分布预测图中未能具体展现这些点位的数据特征，可能是在地统计分析时由于异常值处理和（或）克里金插值的平滑效应被掩盖了。碎片化小区域与其实际的大面积分区区域在空间上呈非连续分布，且通过上述讨论，其内的13 个点位重金属含量呈现不同程度的“异常”，是研究区域内估计和预测重金属含量的关键性点位，在进一步的点位优化筛选研究前，可考虑优先保留这13 个点位，同时将对应的碎片化区域设置为非优化区域，除此之外的大面积分区区域作为最终分区进行研究。

通过主成分−模糊聚类分析方法得到的研究区域空间分区结果并不唯一，分区过程中存在不确定性因素。一是主成分的提取个数的不确定，主成分分析中主成分提取通常考虑特征值（是否大于1）和累计贡献率两个因素，对于土壤重金属污染的主成分分析，纪冬丽等[29]、刘慧琳等[30]采用最大方差旋转法提取特征值大于1 的主成分进行分析，累计贡献率均达85%以上，本研究中主成分提取方法和结果与之一致。二是主成分得分空间分布预测的不确定，对于土壤重金属插值分析，肖艳桐等[31]指出应根据不同的数据分布和影响因素选择适合的空间插值方法，本研究考虑到主成分得分呈对数正态分布，且空间自相关性强，同时为保证分区过程中的精度，通过比较普通克里金插值和反距离权重插值两种方法的交叉验证精度，最终选用精度相对较高的克里金插值对3 个主成分得分的空间分布进行预测。此外，李凯等[32]、谢云峰等[33]指出克里金插值易丢失局部细节，且克里金插值过程中，从数据检验、全局趋势剔除到半变异函数拟合等，每一步的参数确定都会影响克里金插值结果，从而影响均质性分区结果。因此分区过程中对数据进行准确分析并确定较为合适的参数对获得可靠合理的分区结果来说至关重要。

4 结论

（1）Zn、Cd 含量具有强烈的空间自相关性，As、Cr、Pb、Cu、Ni、Hg 含量具有中等程度的空间自相关性，这为通过普通克里金插值方法获得土壤重金属空间分布预测图提供了依据。

（2）利用主成分−模糊聚类分析方法将研究区域划分为3 个均质性分区，通过空间插值图比较和方差分析对分区结果的合理性进行了验证，除Cr 外，其他7 种元素均质性变异系数均小于分区前整个研究区域，分区均合理。主成分−模糊聚类分析方法可对土壤重金属空间变异特征较复杂的区域进行多变量均质性分区，分区后不同分区之间重金属含量差异显著，分区内各重金属含量较为均匀，对区域土壤重金属含量的准确估计与预测具有重要意义，同时为利用均质性分区筛选代表性点位奠定基础。