临近空间高超声速飞行器轨迹预测方法研究进展

邵雷 雷虎民 赵锦

摘要：临近空间高超声速飞行器轨迹预测对其自身制导控制与对其防御拦截均具有重要意义。本文从合作与非合作两个角度对临近空间高超声速飞行器轨迹预测中采用的常用方法进行了分析，在合作飞行器的轨迹预测中，重点结合飞行器预测校正制导过程对解析法与数值法进行了归纳与分析;在非合作飞行器的轨迹预测中，主要分析了基于运动模型预测、基于概率密度预测与基于博弈对抗预测等几种不同轨迹预测方法。最后对轨迹预测的可能研究方向进行了分析。

关键词： 高超声速飞行器;轨迹预测;合作;非合作;拦截

中图分类号：TJ761; V412.4  文献标识码： A  文章編号： 1673-5048（2021）02-0034-06

0 引  言

临近空间高超声速飞行器大多运行于距离地面20～100 km的高空，介于传统航空器与卫星轨道之间的空域，作战高度高于绝大多数地面防空武器，低于大部分轨道拦截器与高层反导拦截器，其潜在的极大的军事应用价值，使其成为世界各国研究的焦点[1-2]。临近空间高超声速武器以高超声速飞行器为载体或直接作为武器本体使用，长时间在临近空间飞行，具有飞行高度高、速度快、突防能力强、打击范围广等特点，对当前防御系统的远程探测发现、跟踪制导、拦截打击等都带来了严峻挑战，能突破目前几乎所有的防御体系，成为进攻方的首选与防御方的难点。

临近空间高超声速飞行器轨迹预测，从合作的角度，可为飞行器自身再入制导过程的轨迹调整提供依据，实现飞行器轨迹在线调整，提高飞行器制导控制性能;也可为地面监测系统提供监测依据，提高对飞行器运行管理能力。另一方面，从非合作的角度，目标轨迹预测是对其拦截的前提，通过对目标的高精度轨迹预测，不但可为防御方尽早制定拦截方案提供数据支撑，也可为拦截过程中，拦截弹发射决策、遭遇点解算、导弹规划与制导控制提供依据。

1 面向合作的临近空间高超声速飞行器轨迹预测方法

针对合作临近空间高超声速飞行器的轨迹预测，通常依托飞行器动力学模型展开，半速度坐标系下的典型运动模型为

r·=vsinγ

φ·=vcosγsinχrcosθ

θ·=vcosγcosχr

v·=-Dm-gsinγ

γ·=1vLcosβm-（g-v2r）cosγ

χ·=Lsinβmvcosγ+vcosγsinχtanφr （1）

式中：h=r-Re为当地高度，Re=6 371 km为地球半径; v为当地速度;γ为当地航迹倾角;χ为当地航迹偏角;φ为经度;θ为纬度;α为攻角;β为倾侧角;D=ρv2CDS/2

为飞行阻力;L=ρv2CLS/2为飞行升力;CD为阻力系数;CL为升力系数;S为特征面积;m为飞行器质量。

从合作的角度，可较为准确地获取目标的当前状态与实时控制逻辑，同时也可得到较为准确的运动模型，即式（1）中飞行器质量m、特征面积S、气动系数CL，CD及控制量α，β均可通过先验特征及任务规划信息获取。因此，面向合作的临近空间高超声速飞行器轨迹预测本质是根据飞行器的当前实时状态，按照一定的方法与规律获取后续时刻的状态，影响轨迹预测精度的主要因素是飞行器气动参数模型的不确定性。

目前，根据预测轨迹原理，合作飞行器主要有两类预测方法：一是在特定条件下，通过式（1）得到运动轨迹解析解;二是基于规划的控制量，通过数值方法得到飞行器轨迹数值解。

1.1 合作飞行器的解析预测方法

解析法是一种较为直观的合作高超声速飞行器轨迹预测方法，预测过程中，通常根据当前状态及先验信息，通过求解式（1）得到飞行器运动轨迹的解析表达式，实现对飞行器的轨迹预测，该方法通常用于弹道式飞行器的轨迹预测[3];但高超声速目标再入过程受气动力的影响，呈现出明显的非弹道特征，很难得到一般意义上的解析解，只能通过合理简化得到一阶或二阶近似解[4]。一些学者尝试不同的方法进行简化与近似，崔乃刚等[5]利用匹配渐进展开法将大气层外的开普勒轨道与大气层内的滑翔弹道相结合，得到了跳跃再入弹道解析解;Lu等[6]将飞行器准平衡滑翔问题看成一类正则摄动问题，认为准平衡滑翔下的纵向轨迹可以看成是平衡滑翔解与其他高阶项解的组合;胡锦川等[7]基于平稳滑翔假设，将升力系数分解为横向分量、平衡滑翔纵向分量和平稳滑翔纵向分量，分别采用解析积分、正则摄动法、高斯积分法和单步龙格-库塔积分获得了滑翔段高度、射程、弹道偏角、经度、纬度和速度的解析解;余文斌等[8]通过简化再入飞行动力学模型，提出了基于线性时变系统的谱分解解析法，获得了再入弹道解析解。

采用解析预测法进行轨迹预测计算速度快、实时性强，但为了获得解析解，需要对运动模式与运动关系进行设定与简化。当综合考虑高超声速目标再入过程运动模式复杂多变的实际情况时，往往很难获得解析解。

1.2 合作飞行器的数值预测方法

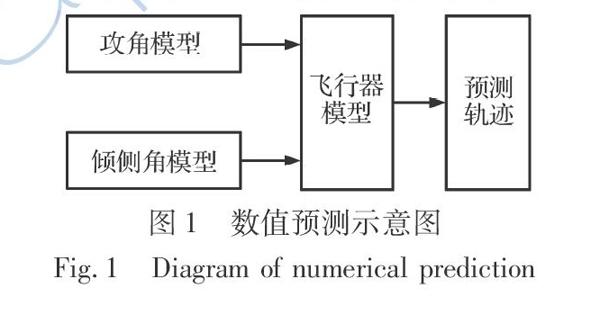
随着高性能计算与处理技术的发展，一些学者也尝试在预测校正制导过程中，采用数值法进行轨迹预测。该方法利用规划的运动逻辑与先验的运动模型通过数值解算方法得到后续时刻的状态[9-11]，为制导过程弹道调整提供依据。典型的预测过程如图1所示，首先设计飞行器的攻角模型和倾侧角模型，然后基于所设计的模型对再入轨迹进行数值预测。

数值预测法能够适应不同运动模式的设计，提高了轨迹预测的适用范围，但受到飞行器运动模型匹配性的影响较大。为了提高计算效率需要对模型进行简化，难免会引入误差;此外，受到高超声速流场复杂不确定的影响，计算模型中采用的气动参数CL，CD等先验信息也会存在一定的偏差，进而影响预测精度。在实际工程应用中，为减少误差，需采用六自由度运动模型进行轨迹预测，但当考虑飞行器的姿态运动时，积分步长必须足够小，从而导致轨迹预测时间大幅度增加，很难满足在线计算的需要，带来了预测精度与计算效率的矛盾。

2 面向非合作的临近空间高超声速飞行器轨迹预测方法

在非合作临近空间高超声速飞行器的轨迹预测中，预测方往往很难获取飞行器的运动模型、控制逻辑等先验信息，即式（1）中飞行器质量m、特征面积S、气动系数CL，CD及控制量α，β均不能直接获取。对飞行器进行轨迹预测的难点，源于高超声速环境下目标特征参数的复杂性与目标未来时刻控制量α，β变化规律的不可预知性。

目前，非合作目标轨迹预测方法研究较多的是数值积分法，与上述合作飞行器轨迹预测过程不同的是，在非合作目标轨迹预测中不能获取目标先验气动参数模型，同时也不能规划目标攻角、倾侧角等控制量变化模型，需要基于歷史跟踪数据与一定的假设条件获取相关模型，进而实现轨迹预测。传统轨迹预测方法假定预测时长较短，目标运动状态变化较慢，直接利用目标跟踪模型进行预测，如CA，CV，CT，Singer，Jerk以及当前统计模型等，根据目标当前状态外推后续状态[12-13]。

随着预测时长的增加，传统预测方法累积误差将逐渐增加，特别是当目标运动模式发生变化时，预测过程将快速发散。这种情况下，如何挖掘与利用目标潜在信息成为提高目标轨迹预测精度的一个关键性问题。根据挖掘与利用目标潜在信息的方式不同，可将预测方法分为三类：一是利用目标运动机理信息，建立预测模型实现轨迹预测;二是采用统计学原理建立相关控制量的概率分布，实现轨迹预测;三是从机动博弈角度，通过引入目标机动意图评估获取目标运动控制量模型。

2.1 基于运动模型的非合作目标轨迹预测方法

为了更好地匹配目标机动特性，提高轨迹预测精度，最为直接的方法是通过对目标运动特性的分析，将目标气动参数、升阻比等运动学特征表述为具有一定规律的关系式，建立目标动力学预测模型。在轨迹预测过程中，首先利用高精度跟踪数据估计这些特征参数，然后分析其变化规律，并基于函数拟合方法给出未来时刻的变化趋势，代入动力学模型进行轨迹预测。典型的控制量拟合函数为

f（a，t）=a1sin（a2t+a3）+a4t+a5（2）

在轨迹预测过程中，利用对控制量的历史估计数据对式（2）中的待拟合参数a=[a1，a2，a3，a4，a5]进行估计，获取目标运动历史过程控制量变化规律，并假定目标运动控制量在未来预测时长内仍按此规律变化，得到预测时刻的运动控制量，实现对目标的轨迹预测。在预测过程中，针对目标不同运动特性的假设可以得到不同形式的目标运动模型，如张洪波等[14]将攻角和倾侧角等控制参数建模成一阶Gauss-Markov过程，利用控制参数的辨识结果对控制参数变化规律进行拟合重构，实现对目标的轨迹预测;王路等[15]认为轨迹预测的关键是获得目标的升阻比，将再入拉起后的升阻比建模成运动状态的函数，通过函数拟合得到升阻比变化关系，并通过数值积分预测轨迹;张博伦等[16-17]在预测模型中引入与气动阻力、升力和侧向力参数相关的状态变量，建立关于目标机动运动状态方程，利用跟踪数据估计并拟合气动参数，并以拟合参数估计控制量实现轨迹预测;张凯等[18]针对高超声速再入滑翔目标跳跃机动的特点，通过研究气动参数的变化规律，递推得到目标运动轨迹。

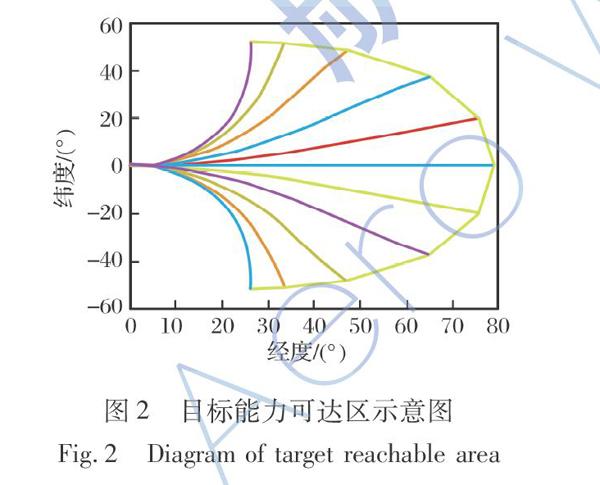
在已知目标准确初始状态与运动模式时，这种预测方法基于目标的动力学方程并通过数值积分外推运动轨迹，能够综合影响飞行器轨迹的各种因素[19]，在获得高精度初始状态以及控制量估计值的条件下，具有较高的轨迹预测精度。但当目标初始状态不准确、目标运动模式发生变化或特征参数辨识不准确时存在较大误差[20]，制约了这类方法的实际运用。在实际高超声速目标轨迹预测过程中，若不对目标机动能力、机动方式等相关动力学特性进行约束，直接利用上述方法进行轨迹预测，其不确定范围实质是目标能力可达区，过大的不确定范围将导致预测结果变得没有价值，如图2所示。

考虑高超声速目标再入过程中，受到环境、热流、过载、动压等众多硬约束，其飞行走廊、机动特性均受到严格约束，一些学者试图通过目标机动特性的分析，约束轨迹预测范围，进一步提高轨迹预测精度。陈小庆等[21]对目标的机动技术进行了研究，但仅分析了目标的机动能力;张裕禄等[22]通过建立简化飞行器动力学模型，分析了平衡滑翔和给定攻角跳跃滑翔两种纵向运动特点，基于给定纵向运动条件下的摆动式和转弯式横向运动分析，建立了横向运动与攻角、倾侧角之间的关系模型;谢愈等[23]通过目标运动方程建立了侧向摆动式机动弹道的弹道形式和倾侧角间的关系模型，分析了高超声速飞行器的机动能力;李广华[24]以攻角和倾侧角为控制量，分析了目标在纵向和横向的可能机动模式以及机动能力，同时提出了可达能力、绕飞能力、转弯能力等飞行器机动能力评估指标;Zhu等[25]研究了一种横向摆动式机动策略，有效提高了高超声速再入滑翔飞行器的突防能力。

2.2 基于概率密度的非合作目标轨迹预测方法

在难以获取目标运动状态先验信息的情况下，基于概率密度的预测方法利用统计学理论，通过对目标历史状态信息的分析，获取目标运动轨迹的统计特征，实现对目标的轨迹预测，基本思路如图3所示。

在实际轨迹预测过程中，结合再入滑翔跳跃目标运动特征，韩春耀等[26]将运动轨迹分解为具有趋势性、周期性和随机性特征的子序列，并分别针对各项子序列特征选择合适的子轨迹预测模型进行回归预测，最后将各预测结果集成为最终预测结果;翟岱亮等[27]将高超声速再入目标历史轨迹中的控制变量看成混沌时间序列进行轨迹预测，在高维矢量空间中描述目标动力学特性，能够在一定程度上应对目标的无规律机动;Chen等[28]采用聚类与非参数估计相结合的方法建立轨迹密度函数，并利用后验处理技术生成轨迹;程媛等[29]采用非参数估计方法，利用先验轨迹数据构建更符合目标实际概率密度分布特征的不确定轨迹预测模型，并通过历史跟踪轨迹数据的KS检测对不确定轨迹预测模型进行匹配，实现轨迹预测;乔少杰等[30]采用高斯混合模型对不同运动模式的概率分布进行建模，使基于历史数据的模型概率达到最大，并采用最小二乘法和高斯混合回归模型训练得到预测模型。

这类方法采用目标统计学特征对目标的局部状态进行建模，避免了目标运动模式不匹配以及参数估计不准确带来的轨迹预测误差，提高了轨迹预测过程的鲁棒性。但这类方法往往以大量先验信息为样本输入，难以适应非合作目标博弈对抗中准确样本信息难以获取的实际问题，采取怎样的途径、什么方法获取目标先验信息成为问题研究的难点。

2.3 基于对抗博弈的非合作目标轨迹预测方法

从博弈论的角度分析，对抗过程中目标的运动总具有一定目的性，若能获取目标运动的这种目的性，则可为目标轨迹预测提供更多潜在信息。利用当前状态与预设先验信息之间的关系判断目标机动意图，对目标机动模式进行合理推理，可提高轨迹预测精度[31-33]，典型预测过程如图4所示。

在实际预测过程中，可通过构造机动意图代价函数进行意图评估，并采用贝叶斯理论迭代推导机动模式和运动状态递推公式[34]，通过蒙特卡洛采样实现轨迹预测。针对意图信息的获取问题，Guillermo等[35]针对合作飞行器，利用飞行手册、规划飞行航路、飞行约束等先验信息与实际飞行状态相结合评估飞行意图;罗艺等[36]采用基于动态贝叶斯网络的推理方法，对高超声速飞行器与攻击目标之间的攻击关系进行推理，预测攻击意图。

引入目标潜在目的性信息，可在一定程度上降低预测过程的信息不确定度，提高轨迹预测精度。但在实际对抗过程中，非合作目标的机动可表现为任务完成的目的性机动与博弈对抗的冗余机动等多种形式，如何准确提炼目标的这种对抗博弈目的性信息，并将其合理引入轨迹预测过程将是提高预测精度的关键。

3 临近空间高超声速飞行器轨迹预测研究发展趋势

飞行器轨迹预测对于提高飞行器自身制导控制性能与提高拦截效能均具有重要意义，特别是在针对高超声速目标的拦截过程中，一定精度的轨迹预测是有效拦截的前提和基础。尽管不少学者从非合作的角度对其轨迹预测问题进行了一定的探索，但受到临近空间高超声速飞行器运动的特殊性与高超声速环境的复杂性等多方面因素的影响，其轨迹预测过程中模型精确辨识、目标机动模式建模以及目标机动模式辨识等问题一直没有得到较好的解决，还有待深入研究。

3.1 基于模型参数辨识的轨迹预测研究

受到复杂高超声速再入环境以及建模过程中简化过程等多方面因素的影响，往往很难建立临近空间高超声速飞行器的精确先验模型，模型的不准确将直接影响到合作飞行器轨迹预测的精度。如何在再入过程中，快速、鲁棒地辨识出模型参数，提高预测模型准确度将是合作飞行器轨迹预测的一个重要问题。

3.2 面向轨迹预测的机动建模研究

临近空间高超声速再入目标可通过气动力控制方式在临近空间进行非弹道式、高速、可持续大范围机动飞行，气动特性随高度大范围变化，这种独特运动特性与临近空间复杂气动环境高度耦合，使其控制方式、突防策略与传统空气动力类、弹道导弹类等目标差异巨大，传统目标轨迹预测模型难以适应这种新特征，如何综合分析这种复杂飞行特征，针对性地建立轨迹预测模型，对于提高非合作飞行器轨迹预测精度具有重要意义。

3.3 基于意图的轨迹预测研究

在难以获得目标准确先验信息的非合作飞行器中，若仅利用飞行器轨迹跟踪所获取的历史统计数据进行拟合性或统计性预测，则飞行器飞行状态以及控制状态等的不确定将对轨迹预测带来较大的不确定，使其轨迹预测过程快速发散。考虑飞行器运动往往具有目的性，若能将这种目的性引入轨迹预测过程，则可在一定程度上提高轨迹预测精度。如何挖掘与利用目标运动的目的性将是预测过程中的一个重要问题。

参考文献：

[1] 姚郁，郑天宇，贺风华，等. 飞行器末制导中的几个热点问题与挑战[J]. 航空学报，2015，36（8）： 2696-2716.

Yao Yu，Zheng Tianyu，He Fenghua，et al. Several Hot Issues and Challenges in Terminal Guidance of Flight Vehicles[J]. Acta Aeronautica et Astronautica Sinica，2015，36（8）： 2696-2716.（in Chinese）

[2] 梁晓庚，田宏亮. 临近空间高超声速飞行器发展现状及其防御问题分析[J]. 航空兵器，2016（4）： 3-10.

Liang Xiaogeng，Tian Hongliang. Analysis of the Development Status and the Defense Problem of Near Space Hypersonic Vehicle[J]. Aero Weaponry，2016（4）： 3-10. （in Chinese）

[3] Battin R H. An Introduction to the Mathematics and Methods of Astrodynamics[M]. Reston：AIAA，1999.

[4] 周軍，水尊师，葛致磊. 一种适用于月球跳跃返回的改进解析预测校正制导律[J].宇航学报，2012，33（9）： 1210-1216.

Zhou Jun，Shui Zunshi，Ge Zhilei. An Enhanced Analytical Predictive Corrector Skip Guidance for Lunar Return Vehicles[J].Journal of Astronautics，2012，33（9）： 1210-1216. （in Chinese）

[5] 崔乃刚，黄荣，傅瑜，等. 基于匹配渐进展开的跳跃式再入解析预测-校正制导律设计[J]. 航空学报，2015，36（8）： 2764-2772.

Cui Naigang，Huang Rong，Fu Yu，et al. Design of Analytical Prediction-Correction Skip Entry Guidance Law Based on Matched Asymptotic Expansions[J]. Acta Aeronautica et Astronautica Sinica，2015，36（8）： 2764-2772. （in Chinese）

[6] Lu P. Asymptotic Analysis of Quasi-Equilibrium Glide in Lifting Entry Flight[J]. Journal of Guidance，Control，and Dynamics，2006，29（3）： 662-670.

[7] 胡锦川，张晶，陈万春. 高超声速飞行器平稳滑翔弹道解析解及其应用[J]. 北京航空航天大学学报，2016，42（5）： 961-968.

Hu Jinchuan，Zhang Jing，Chen Wanchun. Analytical Solutions of Steady Glide Trajectory for Hypersonic Vehicle and Planning Application[J]. Journal of Beijing University of Aeronautics and Astronautics，2016，42 （5）： 961-968. （in Chinese）

[8] Yu W B，Chen W C. Entry Guidance with Real-Time Planning of Reference Based on Analytical Solutions[J]. Advances in Space Research，2015，55（9）： 2325-2345.

[9] Zeng L，Zhang H B，Zheng W. A Three-Dimensional Predictor-Corrector Entry Guidance Based on Reduced-Order Motion Equations[J]. Aerospace Science and Technology，2018，73： 223-231.

[10] Lu P. Predictor-Corrector Entry Guidance for Low-Lifting Vehicles[J]. Journal of Guidance，Control，and Dynamics，2008，31（4）： 1067-1075.

[11] 程阳，程林，张庆振，等. 基于在线约束限制的飞行器预测校正制导[J]. 北京航空航天大学学报，2017，43（10）： 2143-2153.

Cheng Yang，Cheng Lin，Zhang Qingzhen，et al. Aircraft Predictor-Corrector Guidance Based on Online Constraint Limit Enforcement[J]. Journal of Beijing University of Aeronautics and Astronautics，2017，43（10）： 2143-2153. （in Chinese）

[12] Urban M，Manfred M，Thomas I B. Trajectory Prediction for Light Aircraft[J]. Journal of Guidance，Control，and Dynamics，2011，34（4）： 1112-1119.

[13] Woo H，Ji H，Kono H，et al. Lane-Change Detection Based on Vehicle-Trajectory Prediction[J]. IEEE Robotics and Automation Letters，2017，2（2）： 1109-1116.

[14] 张洪波，黄景帅，李广华，等. 典型控制规律滑翔飞行器的轨迹预测方法[J].现代防御技术，2017，45（4）： 112-118.

Zhang Hongbo，Huang Jingshuai，Li Guanghua，et al. Trajectory Prediction of Glide Vehicle Based on Typical Control Law[J]. Modern Defence Technology，2017，45（4）： 112-118. （in Chinese）

[15] 王路，邢清华，毛艺帆. 基于升阻比变化规律的再入高超声速滑翔飞行器轨迹预测算法[J]. 系统工程与电子技术，2015，37（10）： 2335-2340.

Wang Lu，Xing Qinghua，Mao Yifan. Trajectory Prediction of Reentry Hypersonic Glide Vehicle Based on Changing Rule of Lift-Drag Ratio[J]. Systems Engineering and Electronics，2015，37（10）： 2335-2340. （in Chinese）

[16] 张博伦，周荻，吴世凯. 临近空间高超声速飞行器机动模型及弹道预测[J].系统工程與电子技术，2019，41（9）： 2072-2079.

Zhang Bolun，Zhou Di，Wu Shikai. Maneuver Model and Trajectory Prediction of Near Space Hypersonic Aircraft[J]. Systems Engineering and Electronics，2019，41（9）： 2072-2079. （in Chinese）

[17] 翟岱亮，雷虎民，李炯，等. 基于自适应IMM的高超声速飞行器轨迹预测[J]. 航空学报，2016，37（11）： 3466-3475.

Zhai Dailiang，Lei Humin，Li Jiong，et al. Trajectory Prediction of Hypersonic Vehicle Based on Adaptive IMM[J]. Acta Aeronautica et Astronautica Sinica，2016，37（11）： 3466-3475. （in Chinese）

[18] 张凯，熊家军. 高超声速滑翔目标多层递阶轨迹预测[J]. 现代防御技术，2018，46（4）： 92-98.

Zhang Kai，Xiong Jiajun. Multi-Level Recursive Trajectory Prediction for Hypersonic Gliding Reentry Vehicle[J]. Modern Defence Technology，2018，46（4）： 92-98. （in Chinese）

[19] Li X R，Jilkov P V. Survey of Maneuvering Target Tracking： Motion Models of Ballistic and Space Targets[J]. IEEE Transactions on Aerospace and Electronic Systems，2010，46（1）： 96-119.

[20] 李广华，张洪波，汤国建. 高超声速滑翔飞行器典型弹道特性分析[J]. 宇航学报，2015，36（4）： 397-403.

Li Guanghua，Zhang Hongbo，Tang Guojian. Typical Trajectory Characteristics of Hypersonic Glide Vehicle[J]. Journal of Astronautics，2015，36（4）： 397-403. （in Chinese）

[21] 陈小庆. 高超声速滑翔飞行器机动技术研究[D]. 长沙：国防科学技术大学，2011.

Chen Xiaoqing. Study of Maneuvering Technology for Hypersonic Gliding Vehicle[D]. Changsha： National University of Defense Technology，2011. （in Chinese）

[22] 张裕禄，毕红葵，叶泽浩. 高超声速滑翔飞行器典型运动分析与模型设计[J]. 空军预警学院学报，2019，33（2）： 125-129.

Zhang Yulu，Bi Hongkui，Ye Zehao. Typical Motion Analysis and Model Design of Hypersonic Glide Vehicle[J]. Journal of Air Force Early Warning Academy，2019，33（2）： 125-129. （in Chinese）

[23] 谢愈，刘鲁华，湯国建，等. 高超声速滑翔飞行器摆动式机动突防弹道设计[J]. 航空学报，2011，32（12）： 2174-2181.

Xie Yu，Liu Luhua，Tang Guojian，et al. Weaving Maneuver Trajectory Design for Hypersonic Glide Vehicles[J]. Acta Aeronautica et Astronautica Sinica，2011，32（12）： 2174-2181. （in Chinese）

[24] 李广华. 高超声速滑翔飞行器运动特性分析及弹道跟踪预报方法研究[D].长沙： 国防科学技术大学，2016.

Li Guanghua. Motion Characteristics Analysis and Trajectory Prediction for Hypersonic Glide Vehicle[D]. Changsha： National University of Defense Technology，2016. （in Chinese）

[25] Zhu J W，He R Z，Tang G J，et al. Pendulum Maneuvering Strategy for Hypersonic Glide Vehicles[J]. Aerospace Science and Technology，2018，78： 62-70.

[26] 韩春耀，熊家军，张凯，等. 高超声速飞行器分解集成轨迹预测算法[J]. 系统工程与电子技术，2018，40（1）： 151-158.

Han Chunyao，Xiong Jiajun，Zhang Kai，et al. Decomposition Ensemble Trajectory Prediction Algorithm for Hypersonic Vehicle[J]. Systems Engineering and Electronics，2018，40（1）： 151-158. （in Chinese）

[27] 翟岱亮. 高超声速再入滑翔飞行器轨迹预测关键技术研究[D]. 西安：空军工程大学，2016.

Zai Dailiang. Key Technology Study for Hypersonic Vehicle Tra-jectory Prediction[D]. Xian：Air Force Eengineering University，2016. （in Chinese）

[28] Chen C S，Eick C F，Rizk N J. Mining Spatial Trajectories Using Non-Parametric Density Functions[J]. Lecture Notes in Computer Science，2011，6871（1）： 496-510.

[29] 程媛，迟荣华，黄少滨，等. 基于非参数密度估计的不确定轨迹预测方法[J]. 自动化学报，2019，45（4）： 787-798.

Cheng Yuan，Chi Ronghua，Huang Shaobin，et al. Uncertain Trajectory Prediction Method Using Non-Parametric Density Estimation[J]. Acta Automatica Sinica，2019，45（4）： 787-798. （in Chinese）

[30] 乔少杰，金琨，韩楠，等.一种基于高斯混合模型的轨迹预测算法[J]. 软件学报，2015，26（5）： 1048-1063.

Qiao Shaojie，Jin Kun，Han Nan，et al. Trajectory Prediction Algorithm Based on Gaussian Mixture Model[J]. Journal of Software，2015，26（5）： 1048-1063. （in Chinese）

[31] Yepes J L，Hwang I，Rotea M. New Algorithms for Aircraft Intent Inference and Trajectory Prediction[J]. Journal of Guidance，Control，and Dynamics，2007，30（2）： 370-382.

[32] Jimmy K，Dominick A II. Intent Inference with Path Prediction[J]. Journal of Guidance，Control，and Dynamics，2006，29（2）： 225-236.

[33] Liu Y，Li X R. Intent Based Trajectory Prediction by Multiple Model Prediction and Smoothing[C]∥AIAA Guidance，Navigation，and Control Conference，2015.

[34] 张凯，熊家军，李凡，等. 基于意图推断的高超声速滑翔目标贝叶斯轨迹预测[J]. 宇航学报，2018，39（11）： 1258-1265.

Zhang Kai，Xiong Jiajun，Li Fan，et al. Bayesian Trajectory Prediction for a Hypersonic Gliding Reentry Vehicle Based on Intent Inference[J]. Journal of Astronautics，2018，39（11）： 1258-1265. （in Chinese）

[35] Guillermo F，Juan A B，Javier L-L. Generation of Aircraft Intent Based on a Microstrategy Search Tree[J]. IEEE Transactions on Intelligent Transportation Systems，2017，18（6）： 1405-1421.

[36] 罗艺，谭贤四，王红，等.一种高超声速飞行器攻击意图预测方法[J]. 西安电子科技大学学报，2019，46（5）： 113-119.

Luo Yi，Tan Xiansi，Wang Hong，et al. Method for Predicting the Attack Intention of Hypersonic Vehicles[J]. Journal of Xidian University，2019，46（5）： 113-119. （in Chinese）

Research Progress in Trajectory Prediction for

Near Space Hypersonic Vehicle

Shao Lei1*，Lei Humin1，Zhao Jin2

（1. Air and Missile Defense College，Air Force Engineering University，Xian 710051，China;

2. The Institute of Huanghe Group，Xian 710043，China）

Abstract： Trajectory prediction for near space hypersonic vehicle is of great significance to the guidance and intercept. The common prediction methods for near space hypersonic vehicle are analyzed from the cooperation and non-cooperation point.

Firstly，for the cooperation vehicle，the analytic method and numerical method are summed up and analyzed combined with the process of aircraft prediction-correction guidance.

Then，predictions based on  motion model  probability density  and game antagonism are analyzed for the non-cooperation vehicle. Finally，the possible research directions for trajectory prediction is analyzed.

Key words： hypersonic vehicle; trajectory prediction; cooperation; non-cooperation;  interception

收稿日期：2020-06-28

基金項目：国家自然科学基金项目（61773398）

作者简介：邵雷（1982-），男，湖北天门人，副教授，博士，研究方向是空天拦截器制导控制与仿真、武器系统总体技术与作战运用。