变机动高超声速滑翔目标的轨迹序列预测算法

陈南华 赵良玉 雍恩米 娄泰山

摘要：针对变机动临近空间高超声速滑翔目标轨迹难以准确预测的问题，提出一种基于ARIMA-UKF的轨迹预测算法。首先，在目标机动变化情况下通过无迹Kalman滤波（Unscented Kalman Filter，UKF）算法实现对目标的跟踪估计，为轨迹预测提供基础数据;其次，通过对数据进行平稳性分析、模型辨识、参数估计和模型诊断来确定自回归集成滑动平均（Autoregressive Integrated Moving Average，ARIMA）模型，并根据该模型预测目标加速度信息;最后，结合UKF算法中的一步预测方法对目标轨迹进行预测。仿真结果表明，UKF算法能为轨迹预测提供位置误差小于100 m和速度误差小于1.2 m/s的跟踪估计数据;在目标变机动情况下相较于复合函数拟合预测方法，ARIMA-UKF算法预测150 s，100 s和50 s时的位置精度分别提升了5 km，4.5 km和2.3 km。

关键词： 高超声速滑翔目标;轨迹预测;模型辨识;自回归集成滑动平均模型;无迹Kalman滤波

中图分类号：TJ761;V448.2 文献标识码： A  文章编号： 1673-5048（2021）02-0040-09

0 引  言

作為新一代的跨大气层空天飞行器，以HTV-2和AHW为代表的高超声速滑翔飞行器（Hypersonic Glide Vehicle，HGV）是指以马赫数大于5的速度，在临近空间利用自身特殊气动外形提供升力进行无动力滑翔的飞行器[1-3]。其具备突防能力强、毁伤效能高、打击精度准及可快速执行全球任务等优势，受到了各军事强国的高度重视[4-5]。目前，各国专家学者已对HGV的控制特性[6-7]、轨迹优化[8]、跟踪估计[9-10]和轨迹预测[11-15]等问题进行了大量研究。随着HGV的不断发展，来自临近空间的高超声速威胁日益增大，防御方难以对其轨迹进行连续跟踪和准确预测，这极大地影响了拦截作战方案的制定[11，16-17]。因此，研究HGV的轨迹跟踪和预测方法对防御该类目标具有重要意义[9，18]。

HGV目标的连续跟踪是轨迹预测的基础，常使用的跟踪方法为Kalman滤波方法。文献[9]使用线性Kalman滤波方法对HTV-2目标进行跟踪，仿真结果表明目标总位置误差在25 km以内，处于可接受范围之内，证明了Kalman滤波算法的合理性。雍恩米等[10]使用无迹Kalman滤波（Unscented Kalman Filter，UKF）[19]算法在雷达量测模型基础上较好地实现了对滑翔式再入飞行器的跟踪。假设目标运动符合一定规律是实现轨迹预测的前提[4]，文献[11]认为实现轨迹预测的关键是能否对飞行器升阻比进行预测，并根据升阻比线性增长变化的特性，提出基于升阻比变化规律的轨迹预测算法，但该算法是在纵程最优条件下开展的研究，具有一定的局限性。秦雷等[9]以线性Kalman滤波的跟踪结果为基础计算HTV-2当前时刻的控制参数，并通过对运动方程进行动态积分实现目标飞行轨迹的预测，但其使用的线性Kalman滤波跟踪算法仅适用于线性系统。

杨彬等[12]采用广义回归神经网络的方法预测HGV目标飞行轨迹，其核心是通过使用径向基函数逼近非线性运动方程来推导目标飞行轨迹，然而基于神经网络的轨迹预测方法往往受限于训练样本规模，故在仅具有较少的量测数据情况下其预测精度较低。文献[13]在固定攻角和倾侧角的情况下使用交互式多模型跟踪估计目标状态信息，采用一阶多项式和三角函数的复合函数拟合目标气动参数变化曲线，并通过拟合公式预测气动参数信息来预测目标轨迹。魏喜庆等[14]为解决零倾侧角条件下非弹道式高超声速飞行器的轨迹预测问题，在连续跟踪的基础上采用双正弦和函数拟合目标的加速度，然后通过拟合曲线预测加速度信息，进而推导出未来时刻目标轨迹，但其并没有考虑高超声速滑翔目标的机动变化。

目前防御和拦截临近空间高超声速飞行器的作战方式，通常是根据预测轨迹确定拦截弹的发射时机和命中点，拦截弹在进入末制导阶段之前按一定的制导律向预测命中点飞行[20]。但是，由于无法事先准确预知临近空间高超声速目标的真实攻击对象和机动行为，所以如果目标在拦截弹发射后的机动行为发生了变化，则按照前文所述预测轨迹方法得到的命中点也将失效，拦截弹将可能无法顺利完成中末制导交接班，从而导致防御和拦截任务失败。为了解决这一不足，本文考虑日益发展成熟的军用数据链技术[16]，假设拦截弹在发射后仍然具备改变作战区域的能力，即可以根据预测轨迹的变化实时调整预测命中点和相应的制导律，提出一种考虑临近空间高超声速滑翔目标机动变化情况下的飞行轨迹时间序列预测算法。在使用UKF算法对目标状态进行跟踪的基础上，结合自回归集成滑动平均（Autoregressive Integrated Moving Average，ARIMA）模型和UKF算法中的一步预测方法，设计了一种ARIMA-UKF轨迹序列预测算法，并通过数值仿真验证了其有效性。

1 目标模型

1.1 目标运动模型

对于临近空间高超声速滑翔目标而言，其气动力受多方面因素影响：（1）随飞行速度和高度等变化;（2）受目标飞行攻角和倾侧角等控制参数影响;（3）与目标飞行器的特征尺寸密切关联[9]。此外，通过气动力作用引起的加速度变化是临近空间高超声速飞行器滑翔段进行机动的主要原因。因此，为了准确地获取机动变化的目标状态信息，本文在东北天（East-North-Up，ENU）坐标系下描述目标的状态信息，目标运动模型为

xk=Fxk-1+G（g+uk-1）+wk-1=

f（xk-1，uk-1）+wk-1 （1）

式中：xk=[rx，k，ry，k，rz，k，r·x，k，r·y，k，r·z，k]T为ENU坐标系下目标在k时刻的状态向量，（rx，k，ry，k，rz，k）和（r·x，k，r·y，k，r·z，k）分别表示目标的位置和速度;g=[00g]T为重力加速度;uk-1=[ux，k-1，uy，k-1，uz，k-1]T=[x，k-1，y，k-1，z，k-1]T是目标的气动加速度向量;wk-1是均值为零且方差为Qk-1的高斯白噪声;f（·）为目标运动模型函数向量;F和G分别为运动模型的状态转移矩阵和加速度控制矩阵，且可分别表示为

F=I3×303×303×3ΔtI3×3（2）

G=0.5（Δt）2I3×3ΔtI3×3（3）

式中：I3×3为三阶单位矩阵;Δt为时间步长;03×3为三阶零矩阵。

1.2 雷达量测模型

假设量测雷达在目标的整个飞行段均可以连续跟踪。雷达量测模型建立在ENU坐标系中，雷达量测值zk主要由观测距离sk、高低角θk和方位角ηk三个参数组成，如图1所示。

图中，sk为雷达到目标的距离;θk为雷达到目标的连线与ENU坐标系当地水平面的夹角;ηk为雷达到目标连线在ENU坐标系当地水平面内的投影与正东方向的夹角，则雷达量测模型为

式中： vk=[vs，kvθ，kvη，k]T是均值为零且方差为Rk的高斯白噪声;h（·）为雷达量测模型的非线性函数向量。

2 基于UKF的雷达跟踪算法

2.1 UKF算法

Kalman滤波是一种由计算机实现的实时递推算法。在目标跟踪领域被广泛应用[21]，但只适用于系统精确模型已知且噪声为高斯白噪声的线性系统。然而，目标跟踪领域的大多数系统本质上为非线性系统，Kalman滤波算法无法适用，扩展Kalman滤波（Extended Kalman Filter，EKF）应运而生[22]。EKF算法使用一阶Taylor级数展开的方式对非线性系统进行线性化，但忽略了系统高阶项，仅适用于弱非线性系统。

考虑临近空间高超声速滑翔目标系统运动特性的强非线性，本文使用基于UKF的雷达跟踪算法。相较于EKF，UKF算法是对非线性函数的概率密度分布进行近似，而不是对非线性函数进行近似，其选用确定的样本Sigma点来逼近系统状态的后验概率密度，能较好地描述状态的真实均值和方差，避免了计算Jacobian矩阵，且在高斯条件下可达到三阶Taylor级数展开精度。因此，选用UKF算法作为高超声速滑翔目标的跟踪算法，不仅能提升目标跟踪精度，而且也能简化计算的复杂度。UKF算法流程简述如下[19]：

（1）時间更新

2.2 轨迹跟踪场景

本文以HTV-2作为临近空间高超声速滑翔目标的轨迹跟踪和预测对象[23]。假设跟踪目标为质点，忽略地球自转和非球形摄动等因素影响[9]。飞行器质量907.2 kg，特征参考面积0.483 7 m2，初始攻角18.598 2°，初始倾侧角6.428 6°，升力系数和阻力系数选自文献[9]，目标的起始位置为（0 m，0 m，56 279 m），初始速度为3 244.5 m/s，初始航迹倾角-2.056 9°，初始偏航角为90°。HTV-2在ENU坐标系下飞行总时间为883 s，且目标在飞行400 s时通过将东向加速度减小61.68 m/s2来进行机动变化，由原轨迹的命中点1机动变化到命中点2，目标飞行轨迹如图2所示。

为便于计算，设地球为半径6 371.393 km的球体，预警雷达站部署测量位置为（7×104 m，100 m，0 m），雷达的采样间隔Δt为1 s，距离量测误差为100 m，方位角和俯仰角误差均为0.5 mrad。初始协方差矩阵取为

P0=diag102102102101010（18）

2.3 轨迹跟踪分析

使用UKF算法跟踪目标机动变化前后的飞行轨迹，以检验其对目标轨迹跟踪的适用性和有效性。图3为目标机动前后的真实飞行轨迹和使用UKF算法对机动前后飞行轨迹进行跟踪估计的对比图。可以看出，UKF算法对目标机动前后的飞行轨迹均能实现较好地跟踪。图4

是使用UKF算法估计机动前后目标飞行轨迹的位置误差图;图5是使用UKF算法估计机动前后目标飞行轨迹的速度误差图。图4～5中的仿真结果表明，UKF算法对目标机动前的位置估计误差在100 m以内，对机动后目标飞行轨迹的位置估计误差在90 m以内;UKF算法对目标机动前后状态估计的速度误差均在1.2 m/s以内，这与文献[10]中的UKF跟踪估计结果一致。

3 轨迹预测

3.1 ARIMA模型

3.1.1 ARIMA模型概况

自回归滑动平均（Autoregressive Moving Average，ARMA）模型是最常用的拟合平稳序列模型[24]。然而，现实中绝大部分序列都是非平稳的，ARMA的应用受到限制。对于一个非平稳序列而言，其均值、方差和协方差等是时变的，难以通过已知的序列信息展现整体序列的随机性。为解决上述问题，Box和Jenkins于20世纪70年代初提出了以随机理论为基础的时间序列方法，即用于时间序列预测的ARIMA模型[25]。

在时间序列预测ARIMA（p，d，q）模型中，p是表示序列值滞后p阶的自回归系数;d表示时间序列数据转化为平稳数据需要进行的最少差分次数，对应ARIMA模型中的“I”;q是表示误差项滞后q阶的滑动平均系数。ARIMA的实质是对于原始非平稳序列在ARMA的基础上做d阶差分，使序列数据表现平稳特性。此外，ARIMA模型会根据时间序列数据本身的回归构成、随机误差项的回归构成和差分情况具体表现为：自回归模型（Auto-regressive，AR）、滑动平均模型（Moving Average，MA）、ARMA和ARIMA。

3.1.2 ARIMA的数学表示

（3） 参数d的确定

对时间序列数据做自相关平稳检验，根据ACF和PACF的截尾情况来判断数据的平稳性，换言之，如果二者既不是拖尾也不是截尾，则数据为非平稳序列。因此，需要对非平稳序列数据进行差分，直至满足平稳性条件，进而确定差分次数d。

（4） 参数p和q的确定

在序列数据平稳之后，通過ACF和PACF确定参数p，q及模型，如表1所示。

3.1.4 ARIMA建模和预测步骤

（1） 平稳性分析。如果序列数据是非平稳的，可以通过差分使其满足平稳性条件。

（2） 模型辨识。使用ACF和PACF分析平稳序列，并综合差分阶数，确定参数p，d和q。

（3） 参数估计和模型诊断。对模型的参数进行估计，并检验参数的显著性和残差的随机性，然后对比参数拟合结果确定最终模型。

（4） 使用确定后的最终模型进行预测。

3.2 基于ARIMA-UKF的轨迹预测算法

临近空间高超声速滑翔目标轨迹预测问题实质上是状态估计问题，即在历史数据的基础上使用预测方法预测所需要的信息。

在目标轨迹跟踪信息的基础上，通常使用的轨迹预测方法是采用复合函数来拟合目标轨迹的加速度信息，然后使用拟合函数曲线给出未来时刻的加速度信息，进而通过式（1）计算出未来时刻的目标轨迹信息。目前，对加速度信息进行拟合的常用复合函数模型如下所示：

f（t）=b1sin（b2t+b3）+b4sin（b5t+b6）+b7t+b8 （24）

式中：b1，b2，b3，b4，b5，b6，b7和b8为待拟合参数;t为时间自变量。然而，采用此复合函数进行拟合的方式是在目标倾侧角固定情况下进行的，即忽略了目标机动特性[14]。

但是，在实际的高超声速滑翔目标预测过程中，拦截弹发射后仍然存在目标加速度突变的机动变化情况，这会使复合函数拟合预测方法[14]预测的命中点失效，拦截弹无法完成防御和拦截任务。

为了解决临近空间高超声速滑翔目标在机动变化情况下的预测问题，本文考虑日益发展成熟的军用数据链技术，即假设拦截弹发射后仍具备和指挥控制系统进行双向通讯并实时改变飞行轨迹的能力，提出了一种基于ARIMA-UKF的轨迹预测算法。该算法在目标机动变化情况下采用UKF跟踪算法对目标轨迹进行实时跟踪估计，并将跟踪的位置和速度信息作为轨迹预测的历史数据，然后通过使用ARIMA时间序列方法处理历史数据，分析目标加速度信息的变化规律，进而对未来时刻的目标加速度信息进行预测，最后将预测的加速度信息代入目标运动模型式（1）中初步解算出位置和速度信息，并结合UKF算法中的一步预测方法，即式（5）～（9），从而实现目标未来时刻的轨迹预测。如图6所示。

3.3 轨迹预测分析

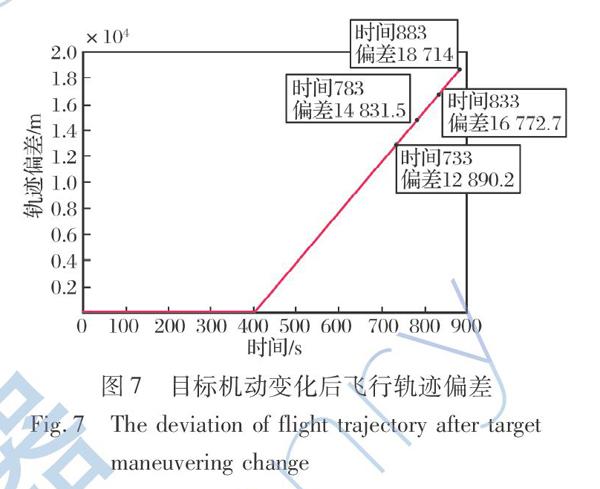
根据2.2节和2.3节中的跟踪场景和仿真分析数据，使用ARIMA-UKF轨迹序列预测算法和式（24）中的复合函数拟合预测方法进行轨迹预测。由2.2节中图2可以看出，目标在机动变化后其飞行轨迹会随时间逐渐偏离原飞行轨迹，目标机动变化后的飞行轨迹偏差见图7。

由图7可以看出，在733 s时目标机动前后的偏差为12.89 km;783 s时和833 s时目标机动前后的偏差分别为14.83 km和16.77 km;在883 s时最终命中点2和命中点1之间的偏差为18.71 km。因此，若不能及时考虑目标机动变化带来的影响，拦截弹仍会按照命中点1的方位进行飞行，并将逐渐偏离目标机动后的命中点2，进而导致拦截任务失败。

采用式（24）中的复合函数拟合预测方法进行预测。即对机动变化前（400 s以前）的目标加速度数据进行分析拟合。在ENU坐标下目标加速度真值和复合函数拟合曲线对比结果如图8所示。可以看出，复合函数拟合预测方法对目标机动后的加速度信息拟合偏差较大。

基于此，假设雷达对变机动目标持续进行量测，在此基础上使用UKF算法跟踪估计目标信息，并使用ARIMA-UKF时间序列预测算法实现对机动变化后目标的轨迹预测。使用ARIMA-UKF时间序列预测算法预测150 s机动变化后的目标飞行轨迹，即基于733 s前的雷达量测数据和UKF跟踪估计数据，预测733 s至883 s之间的目标飞行轨迹。在目标轨迹预测之前，采用提出的ARIMA-UKF算法进行150 s目标加速度信息预测。ARIMA-UKF算法在UKF算法跟踪估计的变机动目标轨迹信息基础上，对目标加速度信息分析处理并确定ARIMA（p，d，q）模型。图9展示了ENU坐标系下目标加速度信息真值、复合函数拟合预测和ARIMA-UKF算法预测150 s的加速度值对比结果，可以看出，使用ARIMA-UKF算法相较于复合函数拟合方法预测的150 s目标加速度信息更加接近真值。

将复合函数拟合预测和ARIMA-UKF预测的150 s加速度信息代入目标运动模型式（1）中，结合UKF算法中的一步预测方法实现733 s至883 s之间的轨迹预测。复合函数拟合预测方法和ARIMA-UKF时间序列轨迹预测算法预测150 s的位置误差和速度误差随时间变化情况如图10～11所示。

从图中可以看出，在733 s之前的位置估计误差较小，这是雷达量测误差造成的;在733 s至883 s之间，复合函数拟合预测方法预测的位置误差在8 km以内，预测的速度误差在120 m/s以内;ARIMA-UKF算法预测的位置误差基本在3 km以内，预测的速度误差在70 m/s以内，且位置误差随时间增加而逐渐增大，这是由于目标轨迹预测过程中存在误差的积累。

根据ARIMA-UKF算法预测的150 s目标轨迹信息控制发射后的拦截弹对机动变化后目标进行拦截。在拦截过程中，雷达持续量测目标飞行轨迹，UKF算法持续跟踪估计，使用ARIMA-UKF算法预测100 s机动变化后的目标飞行轨迹，即预测783 s至883 s之间的目标飞行轨迹。分析783 s之前的目标加速度历史信息，使用ARIMA-UKF算法进行100 s目标加速度信息预测，目标加速度真值、复合函数拟合预测方法和ARIMA-UKF预测100 s加速度值对比结果如图12所示。可以看出，ARIMA-UKF算法相较于复合函数拟合预测方法，预测效果更好;相较于图9中150 s的加速度预测信息，ARIMA-UKF算法预测的100 s加速度信息更精准。

图13～14分别是使用复合函数拟合预测方法和ARIMA-UKF算法预测100 s的位置误差和速度误差随时间变化情况。从图13可以看出，在783 s之前两种预测方法的预测位置误差在100 m以内;在783 s至883 s之间，复合函数拟合预测方法预测的位置误差在6 km以内;ARIMA-UKF算法预测的位置误差在1.5 km以内。由图14中可知，复合函数拟合预测方法预测100 s的速度误差在120 m/s以内;ARIMA-UKF算法预测的速度误差在45 m/s以内。此外，速度误差在增大到一定程度之后开始下降，这是因为图12中的后部分加速度预测值逐渐逼近真值，致使速度累计误差减小。

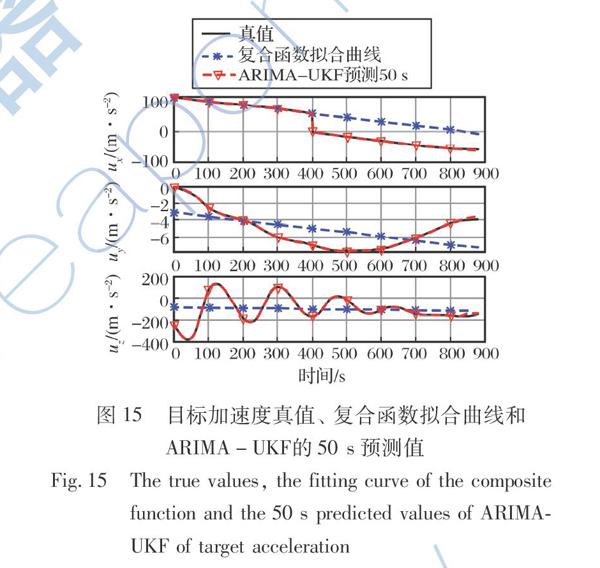
使用复合函数拟合预测方法和ARIMA-UKF时间序列轨迹预测算法预测50 s机动变化后的目标飞行轨迹，即预测833 s至883 s之间的目标飞行轨迹。基于833 s前的目标加速度历史数据，使用ARIMA-UKF算法预测50 s高超声速滑翔目標加速度数据，目标加速度真值、复合函数拟合预测方法和ARIMA-UKF算法预测50 s的加速度值对比如图15所示。可以看出，ARIMA-UKF算法相较于复合函数拟合预测方法的预测效果更为精准;相较于预测150 s和100 s的加速度值，使用ARIMA-UKF算法预测50 s目标加速度值的准确性进一步提高。在目标运动模型式（1）中代入ARIMA-UKF算法预测的50 s目标加速度数据，结合UKF算法中的一步预测方法来预测50 s目标飞行轨迹，即833 s至883 s之间机动变化后的目标位置和速度信息。仿真结果如图16～17所示，其表述了使用复合函数拟合预测方法和ARIMA-UKF算法预测50 s的位置误差和速度误差随时间变化情况。可以看出，复合函数拟合预测方法预测50 s的位置误差和速度误差分别为3 km和120 m/s;ARIMA-UKF算法预测50 s的位置误差和速度误差分别为0.7 km和30 m/s，ARIMA-UKF算法的预测精度更高，其中速度误差的下降和图14中的原因相同，均是速度累计误差减小造成的。

4 结  论

为解决临近空间高超声速滑翔目标机动变化情况下难以对其轨迹进行预测的问题，提出了一种基于ARIMA-UKF的轨迹预测算法。主要结论如下：

（1） 针对目标机动变化情况下的轨迹预测问题，提出了一种ARIMA-UKF轨迹序列预测算法，并进行了仿真验证。在变机动目标的UKF算法跟踪数据基础上，采用ARIMA方法对目标加速度的历史数据进行平稳性处理，并根据模型辨识、参数识别和模型诊断确定目标加速度的ARIMA（p，d，q）模型，然后使用该模型预测未来时刻的加速度信息，并结合UKF算法的一步预测方法对目标轨迹进行预测，通过仿真验证了ARIMA-UKF算法相较于复合函数拟合预测方法在目标机动变化时具有较好的轨迹预测效果。

（2） 在目标883 s的总飞行时间中，目标机动变化后的733 s，783 s，833 s和883 s偏离机动前轨迹的距离误差分别为12.89 km，14.83 km，16.77 km和18.71 km。复合函数拟合预测方法预测150 s，100 s和50 s的位置误差分别在8 km，6 km和3 km以内;预测150 s，100 s和50 s的速度误差均在120 m/s以内。ARIMA-UKF轨迹预测算法预测150 s、100 s和50 s的位置误差分别在3 km，1.5 km和0.7 km以内;预测150 s，100 s和50 s的速度误差分别在70 m/s，45 m/s和30 m/s以内。在目标机动变化后，ARIMA-UKF轨迹序列预测算法相较于复合函数拟合预测方法能较为精准地预测目标飞行轨迹，为拦截弹实时调整飞行轨迹提供了支撑。

（3） 在实际的高超声速滑翔目标飞行过程中，其所处大气环境变化存在强不确定性，机动形式更复杂，如何根据工程应用的可行性，进一步明确目标机动意图;如何针对目标机动特性进行更加符合实际飞行情况的限定或建模;如何针对目标不同机动强度和机动持续时长的情形进行分析，是后续轨迹跟踪和预测的重点和难点。为此，需要进一步研究更加精准的跟踪算法来为预测提供基础数据，研究更多更有效的轨迹预测算法来提升预测实时性和预测精度。

参考文献：

[1] Moses P L，Rausch V L，Nguyen L T，et al. NASA Hypersonic Flight Demonstrators-Overview，Status，and Future Plans[J]. Acta Astronautica，2004，55（3-9）： 619-630.

[2] 赵良玉，雍恩米，王波兰. 反临近空间高超声速飞行器若干研究进展[J]. 宇航学报，2020，41（10）： 1239-1250.

Zhao Liangyu，Yong Enmi，Wang Bolan. Some Achievements on Interception of Near Space Hypersonic Vehicles[J]. Journal of Astronautics，2020，41（10）： 1239-1250. （in Chinese）

[3] 梁晓庚，田宏亮. 临近空间高超声速飞行器发展现状及其防御问题分析[J]. 航空兵器，2016 （4）： 3-10.

Liang Xiaogeng，Tian Hongliang. Analysis of the Development Status and the Defense Problem of Near Space Hypersonic Vehicle[J]. Aero Weaponry，2016 （4）： 3-10. （in Chinese）

[4] 韩春耀，熊家军，张凯，等. 高超声速飞行器分解集成轨迹预测算法[J]. 系统工程与电子技术，2018，40（1）： 151-158.

Han Chunyao，Xiong Jiajun，Zhang Kai，et al. Decomposition Ensemble Trajectory Prediction Algorithm for Hypersonic Vehicle[J]. Systems Engineering and Electronics，2018，40（1）： 151-158.（in Chinese）

[5] 卜祥伟. 高超声速飞行器控制研究进展[J]. 航空兵器，2018（1）： 47-61.

Bu Xiangwei. Progress on Flight Control of Hypersonic Flight Vehicles[J]. Aero Weaponry，2018（1）： 47-61.（in Chinese）

[6] Zhang D，Tang S，Zhu Q J，et al. Analysis of Dynamic Characteristics of the Rigid Body/Elastic Body Coupling of Air-Breathing Hypersonic Vehicles[J]. Aerospace Science and Technology，2016，48： 328-341.

[7] 李传明，孙经广. 基于非线性函数的高超声速飞行器容错控制[J]. 航空兵器，2019，26（3）： 10-18.

Li Chuanming，Sun Jingguang. Fault-Tolerant Control for Hypersonic Vehicles Based on Nonlinear Function[J]. Aero Weaponry，2019，26（3）： 10-18.（in Chinese）

[8] Zhao J，Zhou R. Particle Swarm Optimization Applied to Hyperso-nic Reentry Trajectories[J]. Chinese Journal of Aeronautics，2015，28（3）： 822-831.

[9] 秦雷，周荻，李君龙. 临近空间非弹道式目标跟踪修正变结构滤波[J]. 系统工程与电子技术，2017，39（7）： 1582-1589.

Qin Lei，Zhou Di，Li Junlong. Tracking Filter for Nonballistic Near Space Targets Based on MVSIMM Algorithm[J]. Systems Engineering and Electronics，2017，39（7）： 1582-1589.（in Chinese）

[10] 雍恩米，錢炜祺，何开锋. 基于雷达跟踪仿真的滑翔式再入弹道突防性能分析[J]. 宇航学报，2012，33（10）： 1370-1376.

Yong Enmi，Qian Weiqi，He Kaifeng. Penetration Ability Analysis for Glide Reentry Trajectory Based on Radar Tracking[J]. Journal of Astronautics，2012，33（10）： 1370-1376.（in Chinese）

[11] 王路，邢清华，毛艺帆. 基于升阻比变化规律的再入高超声速滑翔飞行器轨迹预测算法[J]. 系统工程与电子技术，2015，37（10）： 2335-2340.

Wang Lu，Xing Qinghua，Mao Yifan. Trajectory Prediction of Reentry Hypersonic Glide Vehicle Based on Changing Rule of Lift-Drag Ratio[J]. Systems Engineering and Electronics，2015，37（10）： 2335-2340. （in Chinese）

[12] 杨彬，贺正洪. 一种GRNN神经网络的高超声速飞行器轨迹预测方法[J]. 计算机应用与软件，2015，32（7）： 239-243.

Yang Bin，He Zhenghong. Hypersonic Vehicle Track Prediction Based on GRNN[J]. Computer Applications and Software，2015，32（7）： 239-243.（in Chinese）

[13] 翟岱亮，雷虎民，李炯，等. 基于自适应IMM的高超声速飞行器轨迹预测[J]. 航空学报，2016，37（11）： 3466-3475.

Zhai Dailiang，Lei Humin，Li Jiong，et al. Trajectory Prediction of Hypersonic Vehicle Based on Adaptive IMM[J]. Acta Aeronautica et Astronautica Sinica，2016，37（11）： 3466-3475.（in Chinese）

[14] 魏喜庆，王社阳，李瑞康. 基于自适应IMM算法的高超声速飞行器轨迹预测[J]. 上海航天，2016，33（2）： 27-31.

Wei Xiqing，Wang Sheyang，Li Ruikang. Trajectory Predicting of Hypersonic Vehicle Using Adaptive Interactive Multiple Model Filter[J]. Aerospace Shanghai，2016，33（2）： 27-31.（in Chinese）

[15] 邵雷，雷虎民，赵锦. 临近空间高超声速飞行器轨迹预测方法研究进展[J/OL]. 航空兵器，2021. DOI：10.12132/ISSN.1673-5048.2020.0138.

Shao Lei，Lei Humin，Zhao Jin. Research Progress in Trajectory Prediction for Near Space Hypersonic Vehicle[J/OL]. Aero Weaponry，2021. DOI：10.12132/ISSN.1673-5048.2020.0138. （in Chinese）

[16] 邢清华，高嘉乐. 反临作战天海地一体化传感器资源调度的挑战与思考[J]. 航空兵器，2020，27（1）： 1-8.

Xing Qinghua，Gao Jiale. Challenges and Thinking for Sensor Resources Scheduling Based on Space-Sea-Ground Integration in NSHV Defense[J]. Aero Weaponry，2020，27（1）： 1-8.（in Chinese）

[17] 张凯，熊家军，兰旭辉，等. 盲区下高超声速飞行器贝叶斯指示交接方法[J]. 系统工程与电子技术，2019，41（3）： 493-499.

Zhang Kai，Xiong Jiajun，Lan Xuhui，et al. Bayesian Handover Method of Hypersonic Vehicle in Detection Blind Zone[J]. Systems Engineering and Electronics，2019，41（3）： 493-499.（in Chinese）

[18] 孙鹏，杨建军. 临近空间平台防空反导作战运用仿真研究[J]. 弹箭与制导学报，2011，31（2）： 14-16.

Sun Peng，Yang Jianjun. The Study on Proximity Space Platform in Air Defense and Anti-Missile Operation Based on Simulation[J]. Journal of Projectiles，Rockets，Missiles and Guidance，2011，31（2）： 14-16.（in Chinese）

[19] Julier S，Uhlmann J，Durrant-Whyte H F. A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators[J]. IEEE Transactions on Automatic Control，2000，45（3）： 477-482.

[20] 雍恩米，赵良玉，赵暾. 萨德导弹拦截防御作战弹道设计与仿真分析[J]. 空天防御，2020，3（2）： 65-71.

Yong Enmi，Zhao Liangyu，Zhao Tun. Design and Simulation of THAAD Missile Defence Trajectory[J]. Air & Space Defense，2020，3（2）： 65-71.（in Chinese）

[21] Lou T S，Chen N H，Chen Z W，et al. Robust Partially Strong Tracking Extended Consider Kalman Filtering for INS/GNSS Integrated Navigation[J]. IEEE Access，2019，7： 151230-151238.

[22] Sunahara Y，Yamashita K. An Approximate Method of State Estimation for Non-Linear Dynamical Systems with State-Dependent Noise[J]. International Journal of Control，1970，11（6）： 957-972.

[23] 何山，吳盘龙，恽鹏，等. 一种面向临近空间高超声速再入滑翔目标跟踪算法[J]. 宇航学报，2020，41（5）： 553-559.

He Shan，Wu Panlong，Yun Peng，et al. A Tracking Algorithm for Near Space Hypersonic Reentry Glide Target[J]. Journal of Astronautics，2020，41（5）： 553-559.（in Chinese）

[24] 冯盼，曹显兵. 基于ARMA模型的股价分析与预测的实证研究[J]. 数学的实践与认识，2011，41（22）： 84-90.

Feng Pan，Cao Xianbing. An Empirical Study on the Stock Price Analysis and Prediction Based on ARMA Model[J]. Mathematics in Practice and Theory，2011，41（22）： 84-90.（in Chinese）

[25] 闫祥祥. 使用ARIMA模型预测公园绿地面积[J]. 计算机科学，2020，47（S2）： 531-534.

Yan Xiangxiang. Using ARIMA Model to Predict Green Area of Park[J]. Computer Science，2020，47（S2）： 531-534.（in Chinese）

Trajectory Sequence Prediction Algorithm for Hypersonic

Gliding Target with Variable Maneuver

Chen Nanhua1，Zhao Liangyu1*，Yong Enmi2，Lou Taishan3

（1. School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China;

2. China Aerodynamics Research and Development Center，Mianyang 621000，China;

3. School of Electrical and Information Engineering，Zhengzhou University of Light Industry，Zhengzhou 450002，China）

Abstract： A trajectory prediction algorithm based on ARIMA-UKF is proposed to solve the accuracy problem of trajectory prediction of hypersonic gliding target with variable maneuver in near space. Firstly，the Unscented Kalman Filter （UKF） algorithm is used to track and estimate the state of the target under the condition of target maneuver change，which provides basic data for trajectory prediction. Secondly，the Autoregressive In tegrated Moving Average  （ARIMA） model is determined through stationarity analysis，model identification，parameters estimation and model diagnosis of the data，and predicting the acceleration information of the target. Finally，the trajectory of the target is predicted by combining the one-step prediction method in the UKF algorithm. The simulation results show that the UKF algorithm can provide tracking estimation data with position error less than 100 m and velocity error less than 1.2 m/s for trajectory prediction. In the case of target maneuverability，compared with the composite function fitting prediction method，the position accuracy of the ARIMA-UKF algorithm in 150 s，100 s and 50 s is improved by 5 km，4.7 km and 2.4 km respectively.

Key words： hypersonic gliding target;trajectory prediction;model identification;ARIMA;UKF

收稿日期：2021-01-11

基金項目： 国家自然科学基金项目（12072027;11532002）

作者简介：陈南华（1994-），男，河南周口人，博士研究生，研究方向为Kalman滤波和飞行动力学与控制。

通讯作者：赵良玉（1981-），男，河南商丘人，副教授，博士，研究方向为导航制导与控制、飞行器总体设计。