输电塔结构耐受风速的随机分析

2021-08-05张栋余书君范文亮任坤唐正奇

广东电力 2021年7期

张栋, 余书君, 范文亮, 任坤, 唐正奇

(1.佛山电力设计院有限公司，广东佛山528000；2.重庆大学 a.土木工程学院；b.山地城镇建设与新技术教育部重点实验室，重庆 400045)

输电塔是输电线路维持安全稳定运行的重要载体，其可靠性直接关系到整个输电线路的安全。近年来，关于输电塔可靠度的研究逐渐增多，这些研究的思路大致有两类：一是以现有设计规范为对象，研究依据规范设计输电塔构件的可靠度水平[1-7]，或规范中各计算系数对可靠度指标的影响[8]，部分学者亦针对规范设计表达式对应的功能函数中各随机变量的统计参数开展研究[9]；二是以依据规范设计的实际输电塔结构为对象，结合有限元模型和随机分析方法，开展输电塔的静力可靠度[10-12]或动力可靠度分析[13-15]。

可靠度分析对于评估规范的可靠性水平和设计输电塔的安全程度具有重要的作用，但是输电塔结构的抗风能力亦不可忽视，甚至更受工程界关注。然而，与之相应的研究明显偏少，且主要集中于通过试验方法或有限元模拟方法等研究输电塔结构的极限承载力[16-18]。与输电塔可靠度分析相比，这类研究存在如下不足：一方面，没有充分考虑荷载与抗力等的随机性；另一方面，尽管每一输电塔的设计均依据现行规范，但也体现了设计人员的主观性，基于设计输电塔的承载力分析必然包含了主观性的影响，减弱了研究成果的可借鉴价值。

输电塔设计规范体现了输电塔设计中的共性，因此在输电塔的可靠度分析中很多学者针对设计规范开展了共性研究。然而，在输电塔的抗风能力研究方面，针对基于设计规范的输电塔结构耐受风速的随机分析尚属空白，开展相关研究有助于明晰依据现行设计规范设计输电塔耐受风速的底线。为此，本文从设计规范出发，提出输电塔结构耐受风速的随机分析方法，将其应用于特定情况下的耐受风速分析，并通过可靠度比较验证本文方法的正确性。

1 耐受风速的定义

耐受风速是结构所能承受的最大风速。结构失效是与结构的预定功能或极限状态密不可分的，耐受风速与预定功能息息相关，具体而言，耐受风速可以定义为结构在满足预定功能的条件下所能承受的最大风速。

在现有输电线路的设计规范或规程中，杆塔结构的预定功能往往通过承载力极限状态加以保证，如GB/T 50545—2010《110 kV～750 kV架空输电线路设计规范》[19]规定，承载力的极限状态为

γ0(γGSGk+ψ∑γQSQk)≤Rk/γR.

(1)

式中：γ0为杆塔结构重要性系数；γG为恒载分项系数；γQ为可变荷载分项系数；γR为抗力分项系数；ψ为可变荷载组合系数；SGk为永久荷载效应标准值；SQk为可变荷载效应标准值；Rk为抗力在极限状态下的标准值。

事实上，上述承载力极限状态对应的极限状态方程为[20]

R-S=0.

(2)

式中：R为结构的抗力；S为作用在结构上的荷载效应。在设计规范的可靠度校准与可靠度分析中，通常仅考虑简单荷载组合，即荷载效应由永久荷载的荷载效应与1个可变荷载的荷载效应组合来确定，本文亦沿用类似的处理方式。对于耐受风速而言，简单荷载组合下的荷载效应S由永久荷载的荷载效应SG和风荷载的荷载效应SW组合来确定，即S=SG+SW。输电塔所能承受的风荷载可表示为

SW=R-SG.

(3)

本文将此极限状态下的风荷载称为耐受风荷载，记为SWN，与之对应的风速即为输电塔的耐受风速vN。

2 基于设计规范的耐受风速随机分析

2.1 抗力和永久荷载的统计特征

如上文所述，耐受风荷载是在极限状态下的风荷载，在满足规范[19]要求的前提下，抗力在极限状态下的标准值

Rk=γRγ0(γGSGk+γQSWk)，

(4)

式中SWk为风荷载的标准值。

要确定抗力的标准值，需要已知SGk和SWk，然而，基于规范表达式很难给出各标准值的绝对值，可借鉴可靠度分析的思路通过荷载效应比给出相对值，即

ρ=SWk/SGk.

(5)

于是：

(6)

(7)

σR=δRμR，

(8)

(9)

σG=δGμG.

(10)

式中：μR、σR分别为抗力的均值和标准差；KR、δR分别为抗力的均值系数和变异系数；KG、δG分别为永久荷载的均值系数和变异系数。根据文献资料，抗力近似服从对数正态分布[21]，永久荷载服从正态分布[21]，其均值系数和变异系数为KR=1.092、δR=0.108、KG=1.000、δG=0.050[9]，各分项系数为γ0=1.000、γG=1.200、γQ=1.400、γR=1.111[19]。

因此，只要已知风荷载的标准值SWk，就可以结合式(4)—(10)确定抗力和永久荷载的统计参数。

2.2 耐受风荷载的统计特征

通常可假设抗力R和永久荷载SG相互独立，将式(7)—(10)代入式(3)可得耐受风荷载的均值μWN和变异系数δWN为：

μWN=μR-μG=

(11)

(12)

虽然式(11)、式(12)可以确定耐受风荷载的统计参数，但是其分布类型却无法确定。蒙特卡洛法是一种以概率统计理论为基础，通过在电脑上进行大量统计随机抽样来解决数学问题的计算方法。针对任意给定的风荷载标准值SWk(如SWk=1，2)与可取荷载效应比ρ(如ρ=1，2)，均可确定R与SG的统计参数与概率分布，然后结合式(3)进行蒙特卡洛模拟，获得耐受风荷载的SWN的大量样本。基于此样本，一方面可以统计出SWN的均值与变异系数，另一方面可以直接获得其概率密度函数。

表1与表2分别给出了蒙特卡洛模拟得到的SWN的均值、变异系数与由式(11)、式(12)所得结果的对比，不难发现两者结果非常吻合，验证了理论分析的有效性和准确性。

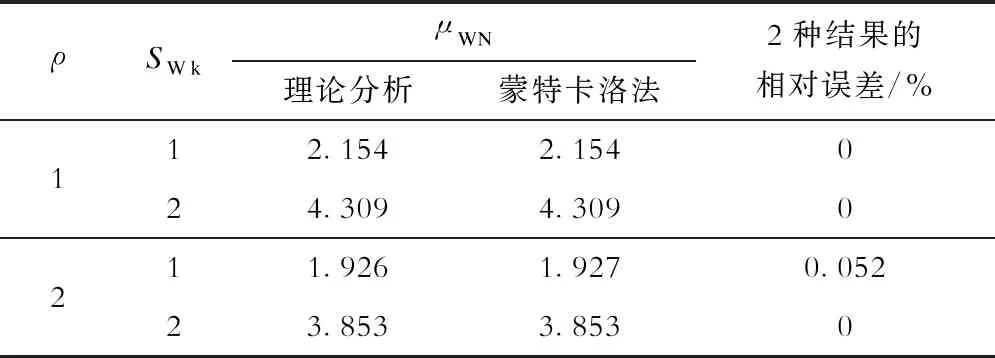
表1 耐受风荷载均值的计算结果

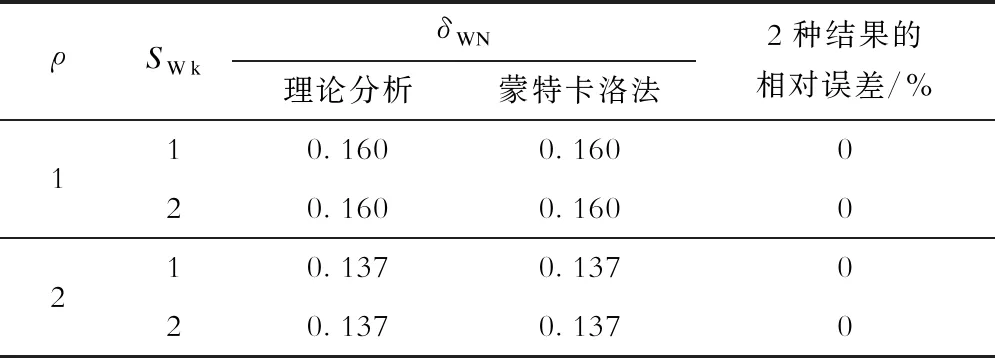
表2 耐受风荷载变异系数的计算结果

图1给出了荷载效应比ρ=1且风荷载标准值SWk分别取1、2的结果，图2给出了荷载效应比ρ=2且风荷载标准值SWk分别取1、2的结果。综合结果不难发现：耐受风荷载SWN均近似服从对数正态分布，与ρ和SWk的取值基本无关。

图1 SWN的分布拟合结果(ρ=1)

图2 SWN的分布拟合结果(ρ=2)

2.3 耐受风速的随机分析

DL/T 5551—2018《架空输电线路荷载规范》[22]规定，杆塔风荷载的标准值

SWk=ω0μzkμskβzkBAsk，

(13)

(14)

式中：ω0为基准风压标准值；μzk、μsk、βzk、Ask分别为按规范确定的风压高度系数、体型系数、风振系数、构件承受风压的投影面积值；B为覆冰时风荷载增大系数(本文取B=1)；v0为基准高度为10 m的风速。

式(13)、式(14)实际上描述了风荷载SW与风速v之间的物理关系，即

(15)

式中μz、μs、βz、As分别为风压高度系数、体型系数、风振系数、构件承受风压的投影面积值的真实值。

基于式(15)描述的物理关系，结合2.2节耐受风荷载的随机分析结果，即可实现耐受风速的随机分析。但是，由于耐受风速与耐受风荷载之间关系的复杂性，直接进行耐受风速的随机分析并不方便。为此，首先进行耐受风速平方的随机分析，然后以此为基础进行耐受风速的随机分析。

2.3.1 耐受风速平方的随机分析

(16)

式中μz、μs、βz、As均服从正态分布，相应的概率信息见表3[21]。

表3 相关参数的概率信息

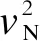
表4 μz、μs、βz、As倒数的概率信息

表5 μz、μs、βz、As倒数平方的概率信息

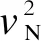
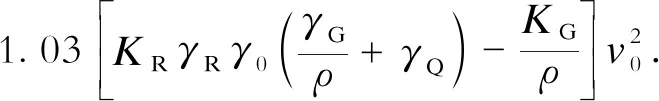
(17)

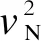
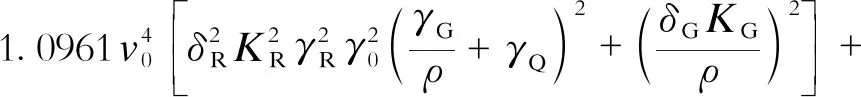
(18)

(19)

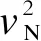
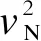
表均值的计算结果对比

表变异系数的计算结果对比

图的分布拟合结果(ρ=1，v0=30 m/s)

图的分布拟合结果(ρ=2，μzk=μsk=βzk=Ask=1)

2.3.2 耐受风速的随机分析

若取基本风速v0=30 m/s与v0=33 m/s，荷载效应比ρ=1与ρ=2，μzk、μsk、βzk、Ask均取1或2，由蒙特卡洛模拟给出的vN的均值和变异系数见表8。

表8 耐受风速的统计参数计算结果

由表8可知：耐受风速的均值随着荷载效应比ρ的增加而减小，且随着基本风速v0增加而增加；耐受风速的变异系数随着荷载效应比ρ的增加而减小，与基本风速v0的取值基本无关。同时，图5给出了基本风速v0=30 m/s，荷载效应比ρ=1，μzk、μsk、βzk、Ask均取1或2时，耐受风速的分布拟合结果；图6给出了基本风速v0=30 m/s与v0=33 m/s，荷载效应比ρ=2，μzk、μsk、βzk、Ask均取1时，耐受风速的分布拟合结果。由图5和6可知：耐受风速vN服从对数正态分布，与ρ、v0、μzk、μsk、βzk、Ask的取值基本无关。