基于深度学习的相位截断傅里叶变换非对称加密系统攻击方法*

徐昭 周昕 白星 李聪 陈洁 倪洋

(四川大学电子信息学院, 成都 610065)

大多数光学加密系统都是对称加密系统, 在光学图像加密中明文和密文之间具有线性关系, 其系统的安全性有待加强. 而基于相位截断傅里叶变换(phase-truncated Fourier transform, PTFT)的非对称加密系统,其非线性的相位截断操作使加密系统的安全性得到了极大提升. 本文提出使用深度学习方法攻击PTFT加密系统, 通过PTFT加密系统构造出明密文对图像数据集, 然后将其输入残差网络(residual network, ResNet)中进行训练, ResNet自动学习该加密系统的解密特性. 最后应用测试集对训练好的模型进行解密性能测试,数据表明该模型能够较好地恢复图像并且该模型具有一定的抗噪声能力. 与两步迭代振幅恢复算法相比, 本文所提出方法恢复的图像质量更好.

1 引 言

在互联网高速发展的时代, 信息安全的重要性不言而喻. 在多种多样的传递信息方式中, 图像是一种重要的载体, 因此保证图像传输的安全得到广泛关注. 数字图像加密是保证图像安全的一种重要技术, 这种技术通常使用计算机等电子手段实现.但是往往受到速度和成本的限制, 基于传统的计算机加密技术需要耗费较长的时间. 随着光信息技术的发展, 光学图像加密技术也取得了长足的进步.光学图像加密技术属于并行加密, 它通过干涉、衍射、傅里叶变换等操作使明文图像变成类似噪声的密文图像, 以光速对图像的所有像素进行加密, 速度快效率高. 光的波长、相位、振幅等都能够作为密钥, 和计算机图像加密算法相比, 光学图像加密具有更高的复杂度和加密自由度.

1995年, Refregier和Javidi[1]首次提出了基于双随机相位编码的光学图像加密算法, 该算法是通过使用两块随机相位板和傅里叶变换来实现. 不过由于该加密算法是对称加密系统, 其线性特性降低了系统的安全性, 因此Qin和Peng[2]在2010年提出了基于相位截断傅里叶变换(phase-truncated Fourier transform, PTFT)的非对称加密系统. 该系统在加密过程中通过相位截断和两块随机相位板生成密文, 而在解密过程中则用与加密密钥不同的解密密钥来恢复密文, 此解密密钥是在加密过程中通过截断处理所产生的. 由于该加密系统是非线性的, 因此系统安全性得到很大提高, 攻击难度较大.

随着人工智能技术的飞速发展以及计算机算力的提升和数据量的膨胀, 深度学习在计算机视觉、生物医学、模式识别等领域都取得了突破进展, 很多算法纷纷涌现并投入到实际应用中. 在深度学习领域有许多经典的神经网络, 如LeNet-5[3],AlexNet[4], VGGNet[5], GoogleNet[6], ResNet[7]等,众多学者在此基础上做出了很多重要工作. 深度学习的特点在于它能使神经网络自动分析数据和数据之间的关系, 因此完全可以利用神经网络的这一特性来研究光学图像加密中明文和密文之间的对应关系, 也就是说可以通过分析它们之间的关系来成功攻击加密系统. Hai等[8]就曾使用卷积神经网络(convolutional neural networks, CNN)成功破解了双随机相位编码的光学图像加密系统, 不过正如前面所说的, 此加密系统是线性且对称的, 安全性较低, 同时破解难度也较低.

本文旨在使用深度学习的方法攻击PTFT加密系统, 该加密系统为非线性且非对称的系统, 破解难度较大. 通过以残差网络(residual network,ResNet)为基础训练大量的明密文对, 使神经网络拟合明文和密文之间的对应关系, 将神经网络训练好之后, 输入密文将可以得到恢复出的原文图像.本文首先介绍了PTFT加密系统原理和ResNet工作原理, 然后阐述了利用ResNet训练图像数据的方法, 最后通过实验验证该方法的可行性, 并且和其他算法所恢复的图像质量进行比较.

2 基本原理

2.1 基于PTFT的非对称加密系统

在基于PTFT的非对称光学图像加密系统中,两块随机相位板R1,R2用作加密密钥, 傅里叶频谱面和输出平面上的截断相位P1,P2用作解密密钥.加密密钥是公开的, 解密密钥只有特定的人才能拥有. 图1为系统的加密解密原理图.

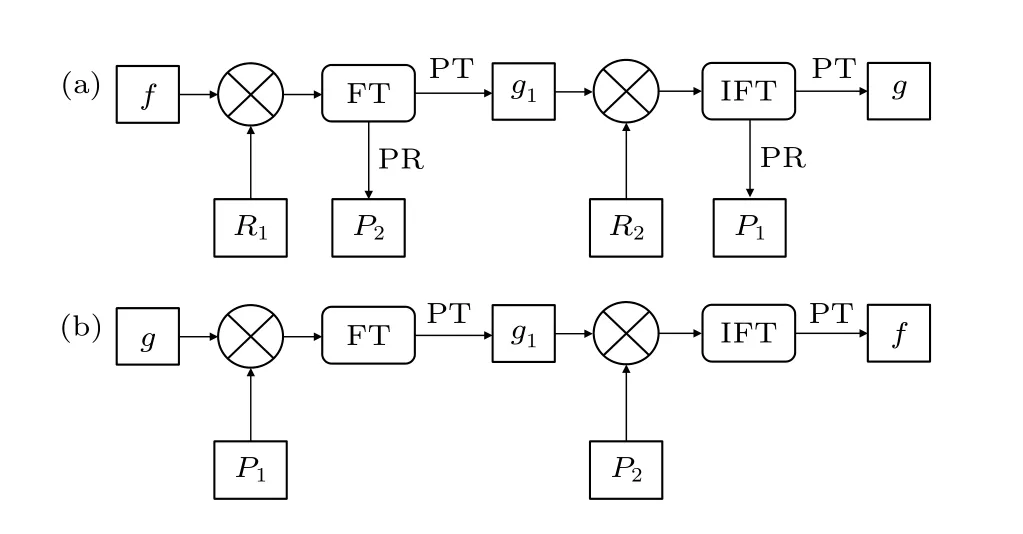
图1 基于PTFT的加密系统原理图 (a) 加密过程; (b) 解密过程Fig. 1. Schematic diagrams of PTFT system: (a) Encryption; (b) decryption.

加密时, 输入图像f(x,y) 乘以第一个随机相位板R1(x,y)=exp[j2πφ(x,y)] , 然后对其进行二维傅里叶变换, 将得到的傅里叶频谱进行相位截断, 截断后的振幅为g1(μ,ν) ,g1乘以第二块随机相位板R2(μ,ν)=exp[j2πφ(μ,ν)], 再进行一次二维傅里叶逆变换得到一个复振幅, 将复振幅进行相位截断便得到了密文图像g(x,y). 加密公式如下所示:

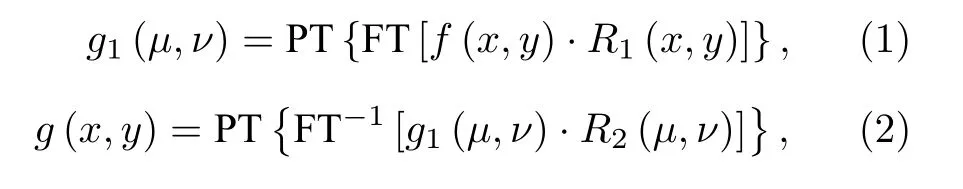
其中PT表示相位截断, FT表示傅里叶变换,FT-1表示逆傅里叶变换.

解密过程如图1(b)所示, 相应公式如下:

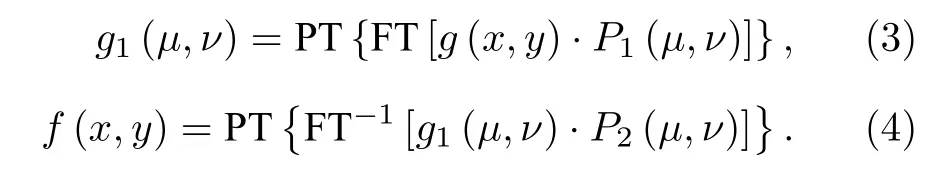
通过上述公式可知, 该加密系统的加密密钥和解密密钥并不相同, 加密过程和解密过程不可逆,为非对称加密系统. 在没有得到解密密钥的情况下无法恢复出原文图像, 因此安全性得到提升, 更容易抵抗传统攻击方法.

2.2 基于ResNet的图像恢复算法框架与实现

传统的CNN中, 随着网络层数的叠加, 特征也越来越丰富, 因此神经网络层数越深, 理论上得到的效果越卓越. 但是简单地增加网络层数会导致两个问题, 一个是在后向传播的过程中不能有效地把梯度传递到前面的网络层, 因此会出现梯度消失或者梯度爆炸的问题, 导致模型无法收敛, 影响网络的性能. 初始化和正则化虽可以保证几十层的网络能够正常收敛, 但是在更深层次的网络中, 准确率达到饱和后效果反而变差. 另一个问题是退化现象, 模型精度下降, 训练错误的频率非常高, 相应的现象在CIFAR-10和ImageNet[9]中都有出现.

因此对于这种问题, He等[7]在2015年提出了残差网络模型(ResNet), 和传统CNN相比, ResNet通过旁路支线将输入传递到后面的网络层, 这种结构称为跳转连接(skip connection)[10], 传统的CNN在传递信息的时候, 会存在信息丢失的问题, ResNet这种直接将输入与输出连接的结构使得神经网络只需要学习输入与输出差别的那部分, 学习更容易了, 这种模型缓解了梯度问题, 让网络学习到的内容更丰富. 其结构如图2所示.

图2 残差网络模块Fig. 2. Residual module of ResNet.

本文提出的基于深度学习的攻击PTFT加密系统的方法是在不知道密钥的情况下对明文-密文对进行选择明文攻击, 因此需要大量的明文-密文对来制作训练集, 将明文-密文对放进神经网络中进行训练, 让神经网络拟合从密文到明文的过程,从而达到解密的效果.

如图3所示, 我们设计的基于ResNet神经网络是一个端到端的结构, 图像加密的过程可以描述为:

其中O是明文图像,I是密文图像, 尽管该加密系统不是一个对称加密系统, 不能简单地进行逆变换进行恢复, 但是神经网络的训练过程可以看作是加密的逆过程, 表示为:

P代表经过神经网络恢复出来的图像.

如图3所示, 尺寸为 6 4×64 的灰度图像先进入卷积层, 卷积层的卷积核的尺寸为 3×3 , 步长为1×1, 用于对输入图像进行特征提取. 此后经过卷积运算的图像数据经过激活层, 激活函数为ReLU[11,12], 如下所示:

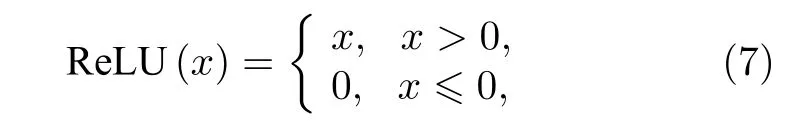
x代表神经网络中上一层的输出, 接下来经过残差模块, 残差模块中包括卷积层、批量归一化(batch normalization, BN)层[13]和激活层, BN层可以加快收敛速度, 提高模型准确性并控制过拟合. 卷积核保持和之前的卷积层一致并输出64张特征图,图3中设置了5个相同的残差模块, 经过5个残差模块后数据又依次被输入到相应的层中, 最后, 我们可以从神经网络中获得 6 4×64×1 的图像.

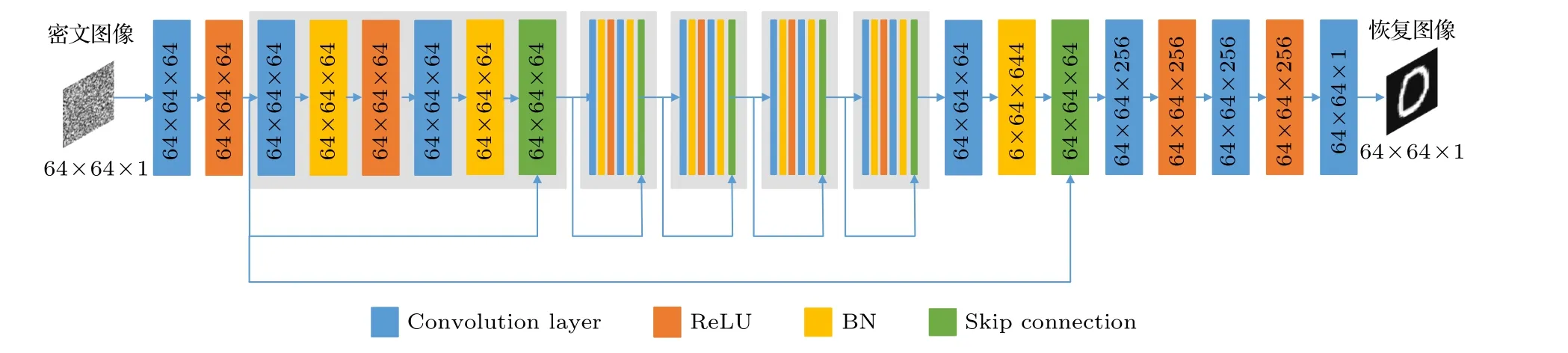
图3 基于ResNet的网络架构Fig. 3. Neural network based on ResNet.

为了更好地恢复密文图像, 本文使用均方差(mean squared error, MSE)损失函数[14,15], 其定义如下:

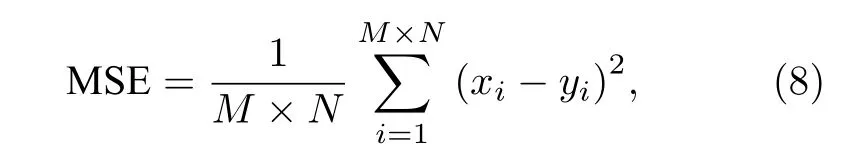
其中xi和yi分别代表最后一层的输出值和原始图像的真值,M和N分别代表图像的宽度和高度, 最后我们期望在训练的过程中最小化损失函数, 当损失函数不再下降时, 训练完成, 模型具有恢复原文图像的能力.

3 实验结果与分析

本次实验的硬件平台采用的CPU是 Intel 至强 E5-2630V4, 内存为16 G, GPU为NVIDIA Ge-Force GTX1080Ti, 编译环境为Python 3.6, 深度学习平台为TensorFlow 1.12. 数据集基于MNIST[16],将所有MNIST数字图像进行PTFT加密得到密文, 由明密文对组成的构成所有的数据集, 训练集中有10000对明密文对, 验证集和测试集中各有1000对, 每张图像的大小为 6 4×64. 其中验证集的目的是调整网络的超参数, 而测试集的目的则是验证神经网络的泛化能力.

实验中学习率设置为0.0001, 优化器采用的是Adam[17], batch size设置为16, 实验结果如图4所示, 图4(a)是明文图像, 图4(b)是密文图像, 图4(c)是通过神经网络恢复的明文图像.

图4 神经网络重建效果图 (a) 明文图像; (b) 密文图像;(c) 通过神经网络恢复的明文图像Fig. 4. Images reconstructed by neural network: (a) Plaintext; (b) ciphertext; (c) plaintext reconstructed by neural network.

为了测试模型的鲁棒性, 可以将高斯噪声添加进密文中, 然后检测其重建效果. 本文使用与密文能量比分别为10%, 20%和50%的高斯噪声得到被污染的密文, 并将其放入测试集中进行测试, 得到图5所示结果. 图5(a)是没有添加噪声的结果,图5(b)是添加10%高斯噪声的结果, 图5(c)是添加20%高斯噪声的结果, 图5(d)是添加50%高斯噪声的结果. 可以看到, 即使密文中带有噪声, 但是恢复出来的图像仍然可以清晰地看到轮廓, 这表明本文提出的模型具有很强的抗噪声能力. 但当密文中带有噪声比例较高如50%时恢复出来的图像失真严重, 已难以辨认, 可以认为该神经网络对噪声的鲁棒性范围在50%以下.

图5 含有不同能量比高斯噪声的密文解密效果 (a) 0%;(b) 10%; (c) 20%; (d) 50%Fig. 5. Reconstruction results of ciphertext containing Gaussian noise with different energy ratios: (a) 0%; (b) 10%;(c) 20%; (d) 50%.

此后, 针对密文含有 2 0% 能量比高斯噪声的情况, 我们尝试让训练集中的密文也被与密文能量比为 2 0% 的高斯噪声污染, 重新制作数据集并重新训练, 再用训练好的网络去处理含有 2 0% 能量比高斯噪声的测试集中的密文, 结果如图6(b)所示.

图6 使用含不同能量比高斯噪声的密文训练集后的测试效果 (a) 0%; (b) 20%Fig. 6. Test results after using ciphertext groups of Gaussian noise with different energy ratios: (a) 0%; (b) 20%.

作为对比, 图6(a)是训练集中密文没有被高斯噪声污染情况下训练好的网络, 对含有 2 0% 能量比高斯噪声的测试集密文重建结果, 可以看到经过噪声训练的神经网络在抗噪声方面表现更佳. 因此在实际中, 如果待处理的密文含有噪声, 可以考虑通过让训练集中的密文也遭受大致相当的噪声污染的方法, 以提高网络的训练效果.

由于在实际应用中, 密文受到噪声污染的比例通常是无法确定的, 因此针对训练集和测试集噪声比例不同做出的测试如图7所示(测试集噪声比例均为30%).

图7 使用含不同能量比高斯噪声的密文训练集后的测试效果 (a) 0%; (b) 20%Fig. 7. Test results after using ciphertext groups of Gaussian noise with different energy ratios: (a) 0%; (b) 20%.

可以看到, 即使训练集和测试集的噪声比例不同, 经过噪声训练的神经网络在恢复被噪声污染的密文时仍然效果更好.

为了评价图像质量, 我们使用峰值信噪比(peak signal to noise ratio, PSNR)和结构相似性(structural similarity index, SSIM)作为参考[18]:

其中X(i,j) 和Y(i,j) 分别代表原始图像和恢复图像的像素值,μX和μY分别是X(i,j) 和Y(i,j) 的均值,σX和σY分别是X(i,j) 和Y(i,j) 的标准差,σXY是X(i,j) 和Y(i,j) 的协方差,C1和C2用来保持稳定性, 使(10)式的分母任意时刻都不为0,k1=0.01,k2=0.03[19],L是像素值的动态范围, 对于实验中的图像,L=255.

图8分别是图6(a), (b)的PSNR和SSIM, 可以从数据上得知, 加入噪声训练过的神经网络, 在恢复有噪声的密文图像时的质量确实比没有经过噪声训练的神经网络恢复的图像质量好.

图8 图6中图像的PSNR和SSIM (a) PSNR; (b) SSIMFig. 8. PSNR and SSIM in Fig.6: (a) PSNR; (b) SSIM.

除了深度学习能够恢复该加密系统加密后的图像, 此前Wang和Zhao[20]曾提出使用两步迭代振幅恢复算法来恢复加密图像. 该算法建立在密文和加密密钥公开的前提下, 可以简单分为两步进行, 第一步求PTFT加密系统中傅里叶平面上振幅分布的近似值, 给输出平面上的相位分布即解密密钥赋一个任意初始值, 根据密文求出迭代第一次的傅里叶平面上的振幅分布值, 由此值求出密文,与真正的密文的均方差表示迭代算法的收敛性. 第二步与第一步类似, 由第一步求出傅里叶平面振幅分布的近似值后, 根据此值和空域的随机相位板迭代出明文图像, 迭代出来的明文和原始明文的均方差表示迭代算法的收敛性. 根据此算法迭代10万次得出图9(b)结果.

从图9中可以直观地看出, 由本文提出的深度学习算法恢复出来的图像质量好于两步迭代振幅恢复算法恢复的图像质量. 而从图10中可以得知深度学习算法恢复的图像的PSNR高于两步迭代法恢复图像的PSNR, 深度学习算法恢复的图像的SSIM均高于0.5, 而两步迭代法恢复图像的SSIM均不高于0.1.

图9 (a)深度学习算法恢复结果; (b)两步迭代振幅恢复算法恢复结果Fig. 9. (a) Reconstruction results by deep learning; (b) reconstruction results by two-step iterative amplitude retrieval approach.

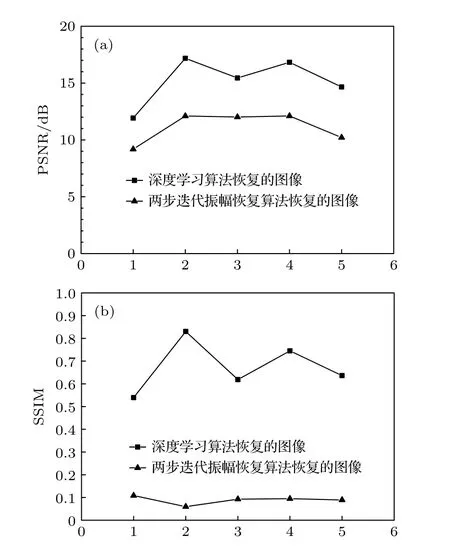
图10 图9中图像的PSNR和SSIM (a) PSNR; (b) SSIMFig. 10. PSNR and SSIM in Fig. 9: (a) PSNR; (b) SSIM.

4 结 论

本文提出使用深度学习的方法攻击基于PTFT的非对称加密系统, 由于该加密系统在双随机加密系统的基础上进行相位截断, 因此该系统是非线性的加密系统, 攻击难度大. 我们从深度学习角度对PTFT系统进行研究, 使用基于ResNet的神经网络训练明密文对数据集, 该网络自动学习密文到明文的拟合过程. 实验结果表明, 通过深度学习的方法能够对密文图像进行有效的恢复, 并且该网络具有一定的抗噪声能力. 与两步迭代振幅恢复算法相比, 本文提出的方法恢复的图像质量也远好于它.在下一步的研究工作中将尝试提高恢复图像的质量, 并对更复杂的加密系统进行攻击研究.