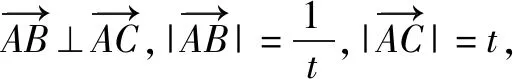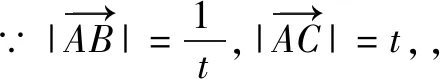借助数形结合思想 推开数学解题之门
2021-08-05马金玲
马金玲
(山东省东营市第一中学 257000)
“数”与“形”有着密切的联系,两者结合起来可获得事半功倍的解题效果,因此教学中应注重数形结合思想的灌输,为学生系统、深入的讲解数学基础知识,使其掌握各种图象绘制技巧,并能根据图象构建正确的图形,灵活用于解答数学习题中,促进其解题能力的显著提升.
一、借助数形结合思想,解答零点习题
零点是高中数学的重要知识点,相关题型在高考中的出现频率较高.解答零点问题应注重根据题意对函数的形式进行转化,以方便的绘制出对应函数的图象,运用数学结合思想将其转化为图象交点问题,问题便迎刃而解.如下题:
已知函数f(x)=3x+x,g(x)=log3x+x,h(x)=sinx+x的零点依次为x1,x2,x3,其大小关系正确的是( ).
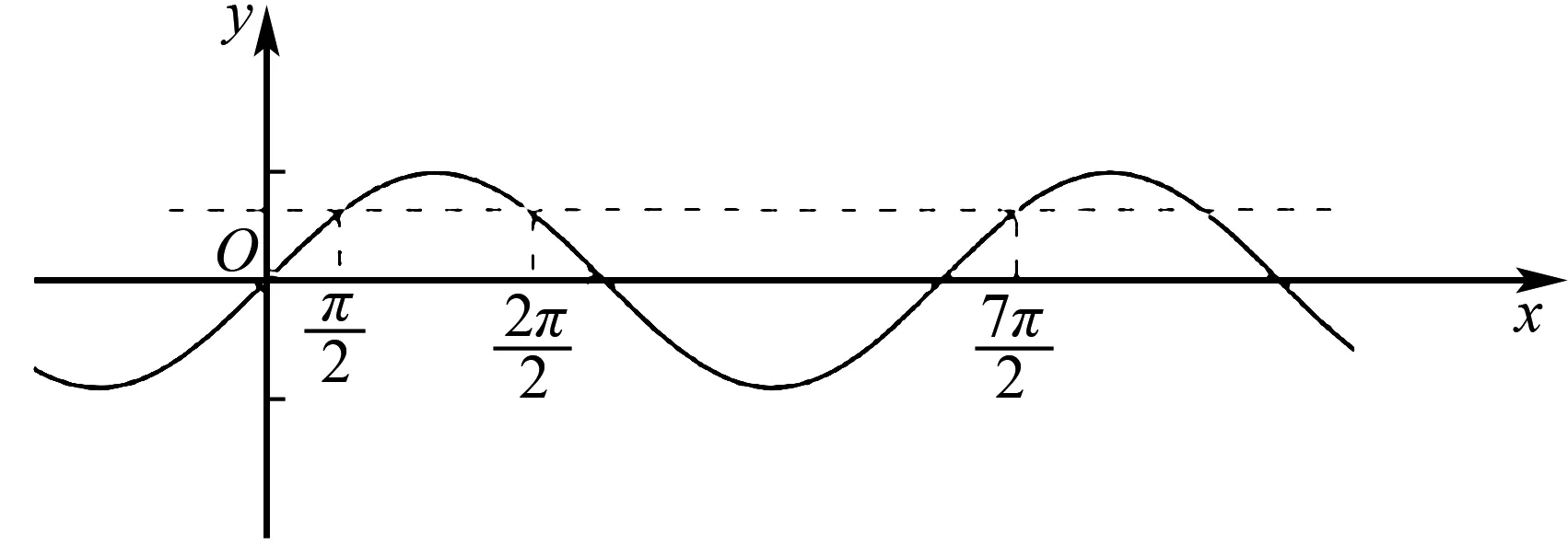
A.x1 C.x3 认真观察三个函数解析式,可知其均含有x,因此可将各解析式拆分成两部分,其零点分别表示函数y=3x、y=log3x、y=sinx和y=-x交点的横坐标.在同一坐标系中绘出的函数图象,如图1所示: 图1 图1 由图可直观的看出三个函数和y=-x图象交点对应的横坐标关系,即,x1 三角函数是高中数学的重要构成部分,尤其求解三角函数表达式中相关参数的取值范围、个数等问题时借助数学结合思想,可直观的看到参数之间的关系,顺利突破题目,因此,解题中应提高数形结合思想应用意识,通过绘制对应的图形,充分挖掘题目隐含条件,高效的解答出相关习题.如下题: A.5 B.6 C.7 D.8 图2 函数与方程联系紧密,尤其一些方程习题通过转化为函数问题,借助函数图象运用数形结合思想能够快速作答.尤其为保证解题的正确性,应注重根据题设准确的绘制出不同定义域内的函数图象,通过函数图象交点迅速的判断出方程根的个数.如下题: A.2 B.3 C.4 D.5 该题目是分段函数和二次函数综合题目难度较大.∵f2(x)-bf(x)=0,则可得f(x)=0或f(x)=b,在平面直角坐标系中画出函数f(x)的图象如图3所示: 图3 由图3可清晰的看到当f(x)=0时,x=0或x=2共两个根;当f(x)=b,0 高中阶段向量既可以单独出题,也可以作为解答其他习题的工具,尤其在解答向量与三角形结合的习题时,通过构建合理的直角坐标系,将向量之间的关系运用坐标表示出来,而后通过坐标的运算进行求解,可迅速解答出难度较大的习题.如下题: A.13 B.15 C.19 D.21 借助数形结合思想解答高中数学习题时,不仅要认真审题,将陌生的问题转化为熟悉的问题,而且还要运用所学知识准确地绘制出各种函数图象以及图形,通过对图象、图形的认真分析,准确的找到相关参数之间的内在关系,在解题中少走弯路,顺利的得出正确答案.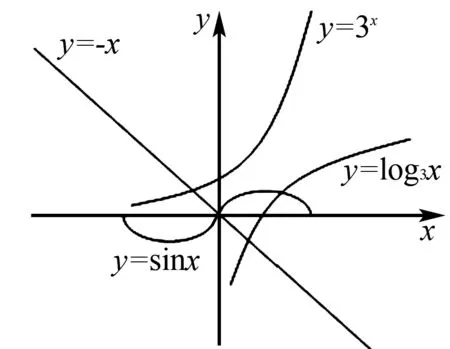

二、借助数形结合思想,解答参数习题


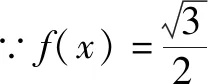


三、借助数形结合思想,解答方程习题
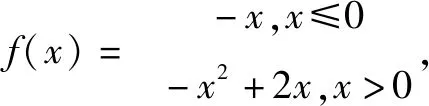
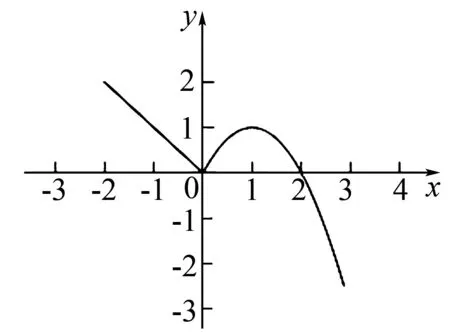
四、借助数形结合思想,解答向量习题