三角形内切圆的方程的求解策略

武增明

(云南省玉溪第一中学 653100)

例题(2010年高考全国卷Ⅰ理科数学第21题文科数学第22题)已知抛物线C：y2=4x的焦点为F，过点K(-1，0)的直线l与C相交于A，B两点，点A关于x轴的对称点为D.

(1)证明：点F在直线BD上；

解(1)设A(x1，y1)，B(x2，y2)，D(x1，-y1)，l的方程为x=my-1(m≠0).

将x=my-1代入y2=4x并整理，得y2-4my+4=0，从而y1+y2=4m，y1y2=4.①

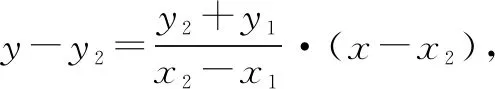
所以点F(1，0)在直线BD上.

(2)方法1(定义法)：由①知，x1+x2=(my1-1)+(my2-1)=4m2-2，x1x2=(my1-1)(my2-1)=1.

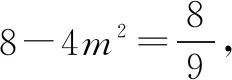
所以l的方程为3x+4y+3=0或3x-4y+3=0.

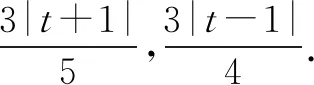
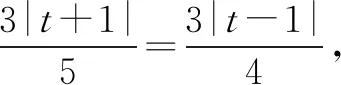
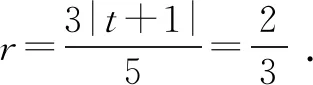
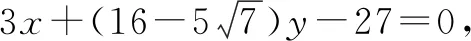
又∠BKD的角平分线所在直线的方程为y=0， ③

评注在这里，方法1和方法2定义法是指三角形内角平分线的定义和三角形内切圆的定义.由三角形内角平分线的定义知，三角形内角平分线上任意一点到这个角的两边的距离相等.由三角形内切圆的定义知，三角形中两个内角的角平分线的交点是这个三角形内切圆的圆心，内切圆的圆心到三角形的一条边的距离是这个内切圆的半径.

方法3(等面积法)：不妨取直线l的方程为3x-4y+3=0，不妨设点A在点B的下方.

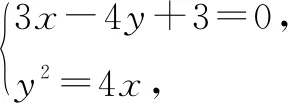
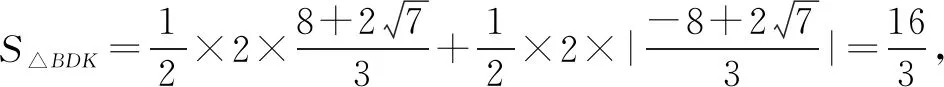
设△BDK的内切圆的半径为r，则

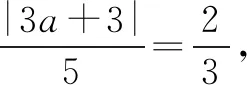
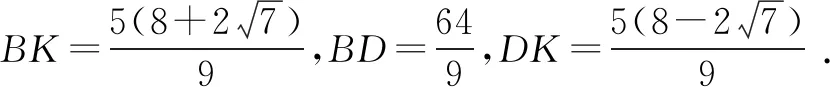
我们知道，若已知一个三角形的三边的长，都可以用再解1求出其面积，在这里是运用余弦定理求cos∠BKD时增加了运算量.

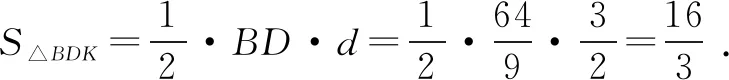
由此解法，我们可以看出，若知道三角形一边所在的直线方程和这边所对的顶点坐标，用再解2来求三角形的面积时运算量会减少很多.

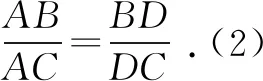
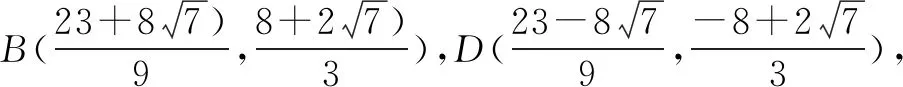
=0.

本文给出求解三角形内切圆方程的四种方法，何时用哪种方法求解速度快？没有规律可循，可以说很灵活，但是只要同学们认真领悟并掌握这五种方法，解决三角形内切圆方程的问题就没有问题了.