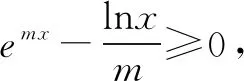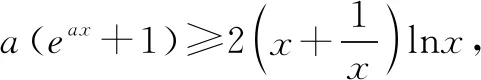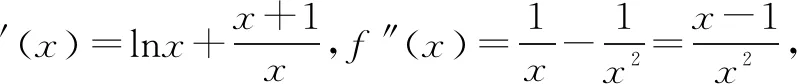同构式解题举隅

蒋满林

(福建省古田县第一中学 352200)

一、预备知识

指对混杂恒等式：xex=lnex·ex=tlnt(t=ex);xlnx=elnx·lnx=tet(t=lnt).

这两个恒等式就是通常所说的指对混杂同构式，简称同构式，它在解决某些指、对函数混杂问题往往能收到时事半功倍的效果，下面结合例子说说同构式的具体应用.

二、同构式解题

1.利用同构式求参数范围

例1(2020山东21，海南22题)已知函数f(x)=aex-1-lnx+lna.

(1)略；

(2)若f(x)≥1，求a的取值范围.

评注构造同构式ex-1+lna+x-1+lna≥x+lnx=elnx+lnx，再利用函数g(t)=et+t的单调性进行解题，避免了遇字母就讨论的基本思路，创新思维视角、简化过程计算，提高解决问题的能力.

2.利用同构式求参数最值

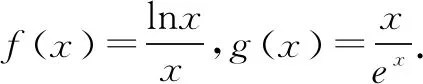
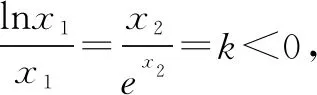
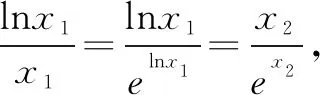
3.利用同构式证明不等式

例3 已知函数f(x)=2x-lnx.

(1)求函数f(x)的单调区间；

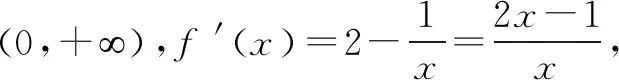
4.利用同构式计算函数值

例4 已知x0是函数f(x)=x2ex-2+lnx-2的零点，计算e2-x0+lnx0的值.

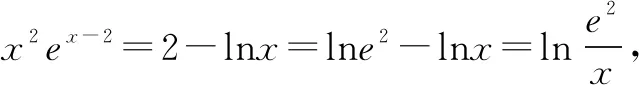
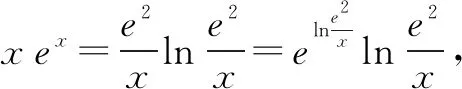
三、变式练习

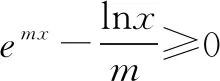
2.已知函数f(x)=2ae2x-lnx+lna，若f(x)≥0恒成立，求实数a的最小值.

附参考解答