基于多元线性回归的真菌分解过程分析

马秋敏，杨 洪，2，于亦飞

（1.江苏海洋大学 理学院，江苏 连云港 222005；2.江苏省海洋资源开发研究院（连云港），江苏 连云港 222005）

碳循环描述了碳在整个地球化学循环中的交换过程，是自然界中物质和能量循环的重要组成部分。碳循环的一部分包括化合物的分解，允许碳被更新并以其他形式使用。这部分过程的一个关键组成部分是植物材料和木质纤维的分解，而分解木质纤维的关键因素是真菌。2021年美国大学生数学建模竞赛A题要求用数学建模的方法研究真菌分解木质纤维素纤维过程及其相互作用问题。本文拟采用修正Frisch法、最小二乘法、微分方程等研究真菌分解木质纤维素纤维的过程，以及不同种类真菌间的相互作用、在环境影响下的真菌生存能力。

1 “真菌分解速率”模型的建立与分析

1.1 模型建立

基于题中给出的假设条件，以及影响真菌的外部影响因素（湿度、菌种间的影响、pH值等）和内部影响因素（真菌的内在性状，如生长速度、耐湿性等），并且假设存在下列相关系数a，b，c，d，构建真菌分解速率y与影响因素间的多元线性回归模型[1]：

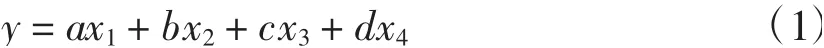
其中，x1为真菌的耐湿性，x2为真菌生长率，x3表示菌种间的影响，x4为pH值，y为真菌分解速率。

1.2 模型求解

由赛题资料可知，真菌分解速率y和生长率x2呈线性关系，真菌分解速率y与耐湿性x1呈正比关系。进一步研究真菌耐湿性x1、真菌生长率x2对真菌分解速率y的影响，根据生长率x2与分解速率y2的数据，利用Eviews软件作x2与y2的散点图如图1所示。由图1可见，x2与y2近似呈对数关系。

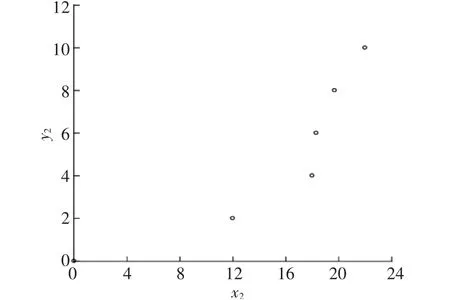
图1 真菌生长率x2与分解速率y2关系

将真菌生长率x2与真菌分解速率y2进行线性回归，运用最小二乘法得到估计结果如图2。

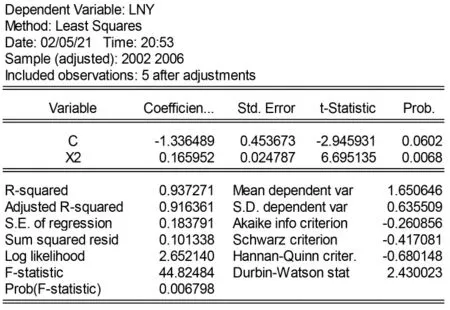
图2 x2与ln y2最小二乘估计结果

由图2可知，

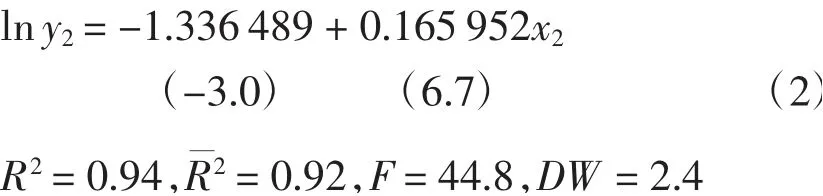
其中，括号内的数字是t值。R2=0.94说明总离差平方和中有94%被样本回归直线解释，只有6%未被解释。可见回归方程拟合结果较好，且t检验和F检验均符合要求，回归方程显著。

将（2）式化简可得：

同理，得到耐湿性x1与分解速率y1的最小二乘估计结果如图3。

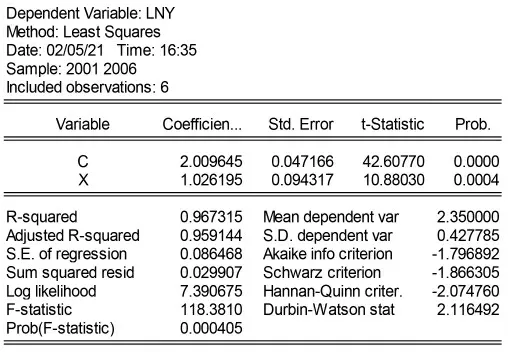
图3 x1与ln y1最小二乘估计结果

由图3可得

其中括号内的数字是t值。R2=0.97说明总离差平方和中有97%被样本回归直线解释，只有3%未被解释。表明回归方程拟合结果较好，且t检验和F检验均符合要求，回归方程显著。

将（4）式化简可得：

同时，在处理真菌耐湿性与生长率关系时，可发现不同真菌耐湿性和生长率大致呈线性关系（这里的线性关系可看作广义的二元关系，只要两个变量直接有关联即可）。因此，在保持真菌分解速率不变的情况下将两种因素进行合并，其拟合方程为：

将不同因素影响下的y1、y2进行加总，得出合并处理后的真菌分解速率模型为：

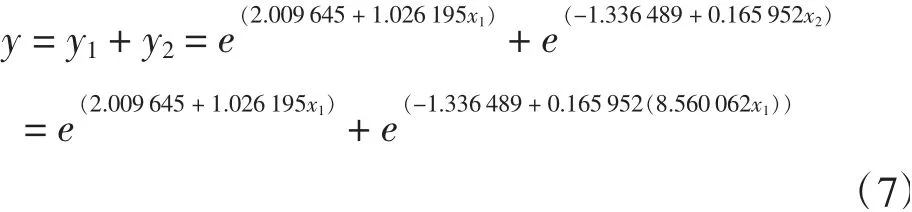
2 真菌间不同关系模型的建立与分析

2.1 竞争关系模型的建立与求解

（1）竞争关系标准模型如下：

其中：x5、x6分别为A、B菌种在t时刻的数量；rA、rB为A、B菌种的固定增长率；NA、NB是环境资源容许的菌种最大数量；σ1表示对于供养A菌种的食物量而言，单位数量B菌种（相对NB）的消耗为单位数量A菌种（相对NA）消耗的σ1倍；σ2表示对于供养B菌种的食物量而言，单位数量A菌种（相对NA）的消耗为单位数量B菌种（相对NB）消耗的σ2倍[2]。

（2）模型求解

对于两种有竞争关系的真菌而言，当为了生存争夺有限的同一食物来源和生活空间时，竞争力较强的种群往往达到环境允许的最大数量。任取有竞争关系的A菌种和B菌种，其中，A菌种是生长缓慢的真菌菌株，更适应在变化的环境下生存和生长，而B菌种生长速度较快，但在相同的环境变化中不那么茁壮。因此，A菌种固定增长率rA小于B菌种固定增长率rB，而A菌种的竞争能力高于B菌种，即σ1>σ2；在环境适宜时，取rA=0.2，rB=0.5；σ1=2，σ2=0.5，获得A、B菌种的数量关系与相轨线如图4。

由图4可见，最后数值稳定于x6=0，x5=10，即A菌种达到最大数量，B菌种灭绝。

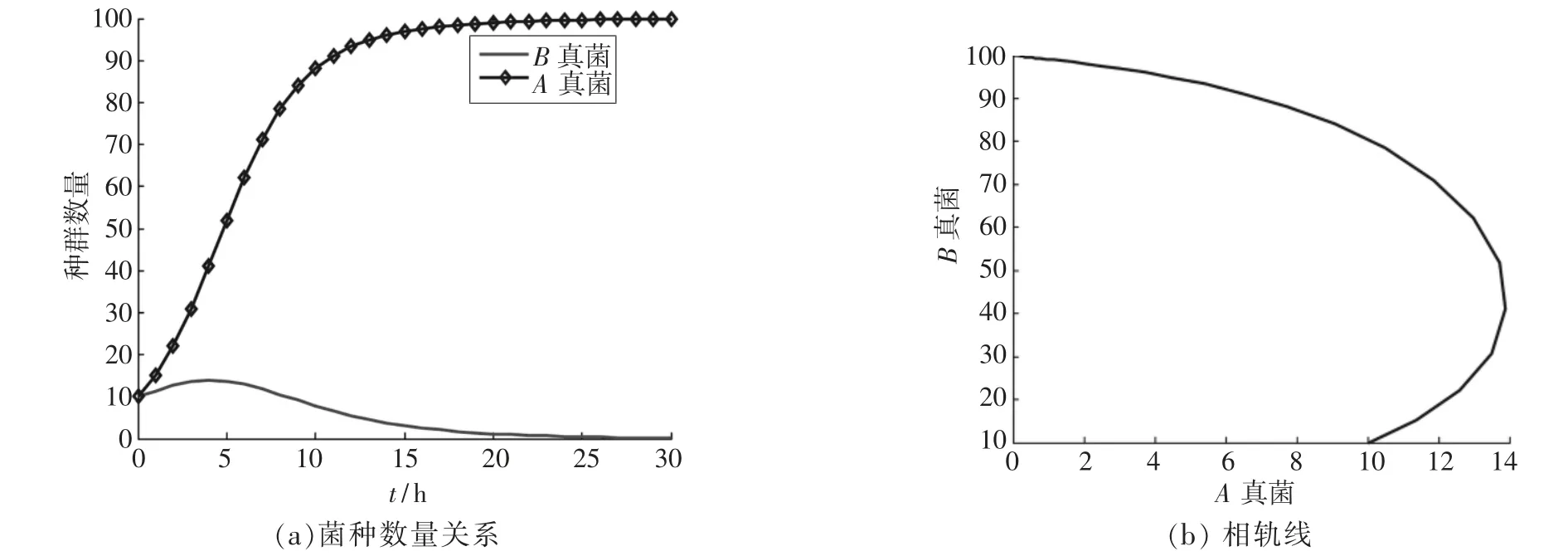
图4 A菌种与B菌种数量关系及相轨线

环境变化导致了A、B菌种的自然增长率的快速变化。取rA=0.4，rB=0.3，σ1=2，σ2=0.5，获取A、B菌种的数量关系与相轨线如图5。

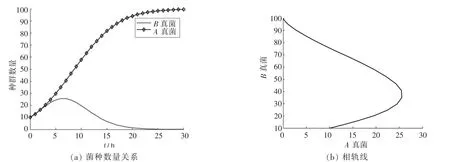
图5 自然增长率变化后的A、B菌种数量关系与相轨线

2.2 捕食关系模型的建立与求解

任取C菌种和D菌种，假设其是捕食关系，其中C菌种是捕食者，D菌种是被捕食者。C菌种主要以木质纤维中的营养物质和D菌种为食，且当捕食D菌种到一定程度则不再捕食；D菌种主要以木质纤维中营养物质为食。

利用Volterra食饵-捕食者模型来解决以下问题：

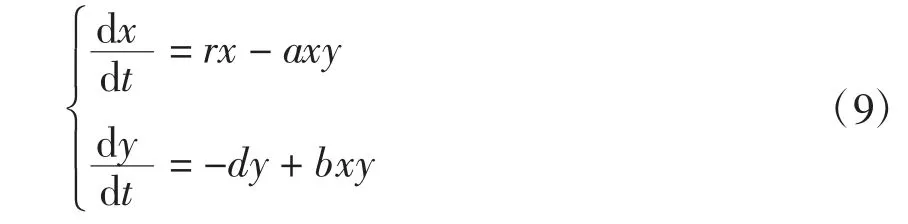
其中：t为时间，x（t）、y（t）为D、C菌种在t时刻的数量；r为D菌种独立生存时的增长率；d为C菌种独自存在时的死亡率；a表示C菌种掠取D菌种的能力；b表示D菌种对C菌种的供养能力。

C菌种主要以木质纤维中营养物质和D菌种为食，当环境快速波动时，仍可以D菌种为食生存；而D菌种主要以木质纤维中营养物质为食，当环境快速波动时，则极易死亡。

取C菌种初始值为150，D菌种初始值为300，当环境适宜时，取r=2，d=1，a=b=0.01代入上述方程作菌种数量关系和相轨线如图6。

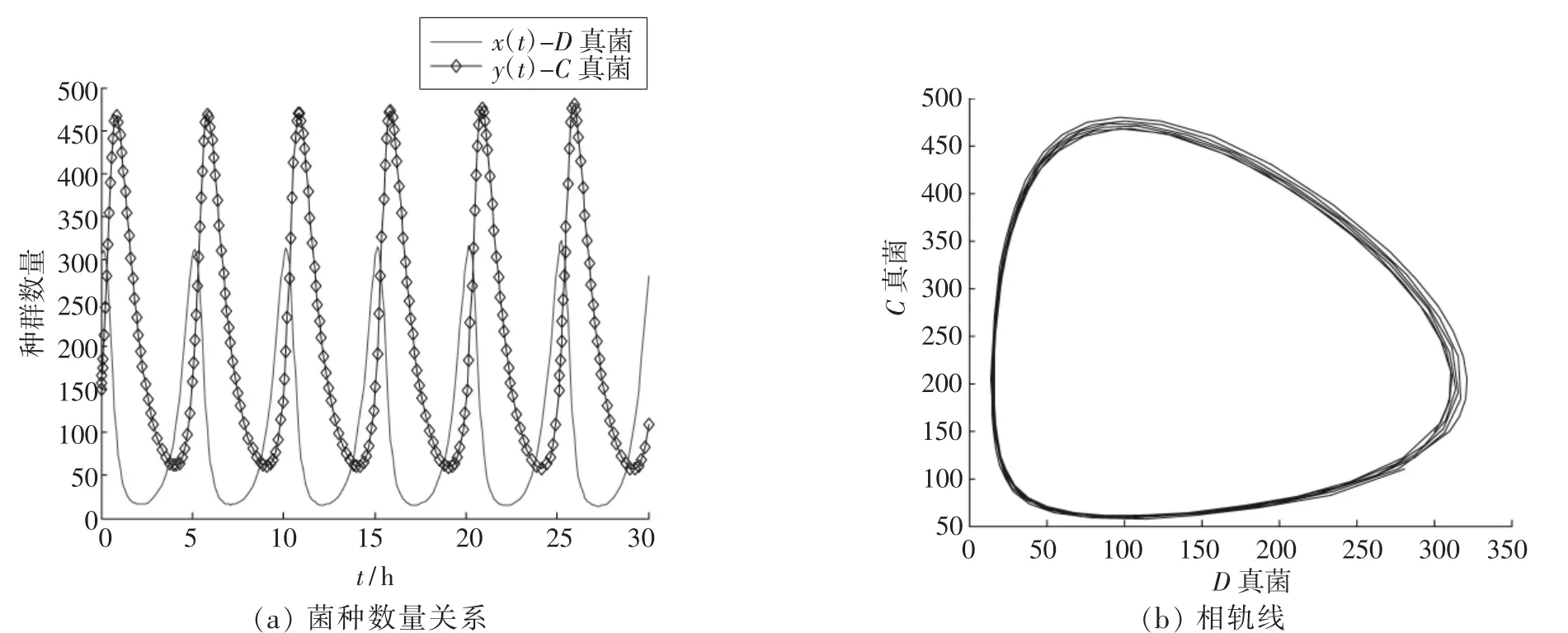
图6 捕食关系的C、D菌种数量关系及相轨线

由图6可见：C、D两菌种相互制约，当C菌种逐渐增多时，D菌种逐渐减少；当C菌种增加到一定数量时，由于种群内部竞争激烈，又导致其数量减少，从而使得D菌种天敌减少，进而导致D菌种数量增加；当D菌种增加到一定数量时，种群间竞争加剧，从而又导致D菌种数量减少。如此循环，相互制约发展。

当环境快速波动时，取r=2，d=1，a=b=0.05，代入方程得图7。从图7可以看到，C、D两菌种仍满足上述关系，且在环境恶劣时，其数量变化较为显著。

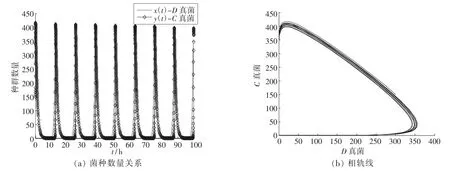
图7 D菌对C菌供养能力变化后C、D菌种的数量关系及相轨线

2.3 互利共生关系模型的建立与求解

对于相互依存的两种真菌而言，相互依存而共生是其普遍现象。任取互利共生关系的E菌种和F菌种进行研究，其中，E菌种可单独存在，F菌种为E菌种提供食物，同时不能离开E菌种单独存活，且有助于E菌种的生长。

建立模型如下：

其中：x7、x8为E、F菌种在t时刻的数量；rE、rF为E、F菌种固定增长率；NE、NF是环境资源容许的E、F菌种最大数量；σ3表示对于供养E菌种的食物量而言，单位数量F菌种（相对NF）的消耗为单位数量E菌种（相对NE）消耗的σ3倍；σ4表示对于供养F菌种的食物量而言，单位数量E菌种（相对NE）的消耗为单位数量F菌种（相对NF）消耗的σ4倍。

在温度适宜时，取rE=1.8，rF=1.5；σ3=0.1，σ4=3，作菌种数量关系与相轨线如图8。

图8 互利共生关系的E、F菌种数量关系与相轨线

从图8可看出，当t趋于无穷大时，两种真菌的最大数量均增大且相互依存，在无外界因素剧烈变化的条件下，两种真菌数量趋于稳定。

当环境快速波动时，取rE=1.8，rF=1.5；σ3=0.3，σ4=3，得到E菌和F菌的数量关系及相轨线如图9。

图9 σ3变化后E、F菌种数量关系及相轨线

从图9可看出，在环境快速波动时，随着σ3的增加，两种真菌间共生率增大，表明其促进作用也增大，且两种真菌数量随时间增加达到平衡位置的值也增大。

3 不同环境影响下真菌分解速率模型

3.1 模型的建立

不同种类真菌的耐湿性和生活的最佳温度都和真菌生长率有着密切关系，也决定了真菌最适宜的生存环境条件。针对这两种因素建模，分析其最适宜的生存环境条件，最终得到真菌生长率与真菌所处环境的温度和耐湿性的关系式。

3.2 模型求解

由赛题所给条件可得生长率x2、温度x3与耐湿性x1的数据，利用Eviews软件作x2与x1的散点图如图10。由图10可见，x2与x1近似呈对数关系。

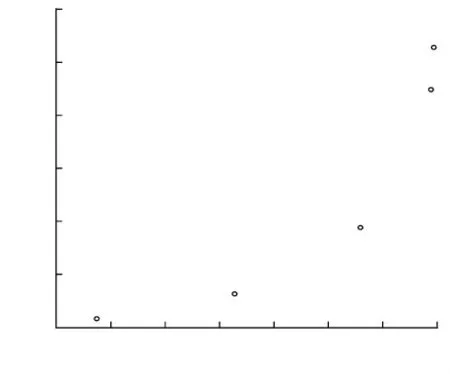
图10 x1与x2散点图

将真菌生长率x2与真菌分解速率x1进行线性回归，运用最小二乘法得到估计结果如图11。

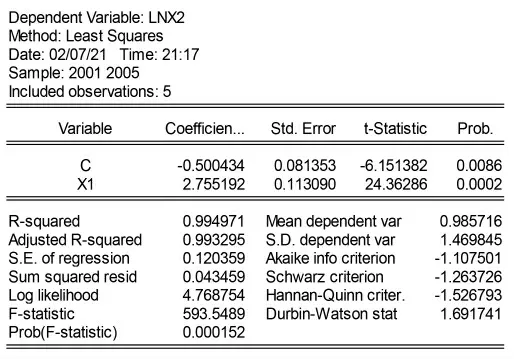
图11 ln x21与x1的最小二乘估计结果

由图11可得

R2=0.99，R¯2=0.99，F=593.54，DW=1.69其中，括号内的数字为t值。R2=0.99说明总离差平方和中有99%被样本回归直线解释，只有1%未被解释。可见回归方程拟合结果较好，且t检验和F检验均符合要求，回归方程显著[3]。

将（11）式化简可得：

同理可得图12的散点图。由图12可见，x2与x3近似呈线性关系。

图12 x2与x3散点图

拟合得x22=-2.194952+0.397 525x3

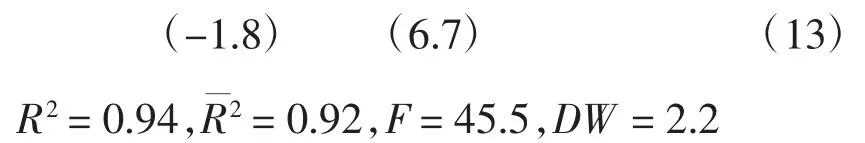
由t检验可知，常数项不显著，故舍去。再次拟合得：

按上述步骤检验，得知回归方程显著。

综上可得，真菌生长率与温度及耐湿性的关系式为：

假设温度为5~35℃，且x3的系数为正，由式（15）可知，温度对生长率始终起促进作用。为指数函数，且当-0.500434+2.755192x1>0时，即x1>0.181633时，为单调递增函数，即真菌的生长率随着温度与耐湿性的增大而增加。反之，若-0.500 434+2.755 192x1<0，则为单调递减，且当x1→∞时，x21→0，即真菌生长率只与温度有关。

分析表明，干旱地区与半干旱地区真菌的耐湿性最弱，且干旱地区与半干旱地区昼夜温差较大，因此真菌生长率较低。乔木林和热带雨林地区真菌的耐湿性最强，因此可视为只受温度的影响，其生长率与温度成正比关系。温带地区真菌耐湿性较强，且温度适宜，生长率明显高于干旱地区、半干旱地区及乔木林和热带雨林地区，适宜真菌生长[4]。