基于翻转课堂理念探讨混合式教学模式在中职数学教学中的应用

林晓文

【摘要】翻转课堂是近年来教学的一种新形式，是实现混合式教学的有效途径，可以实现教学模式的创新和发展.本文重点研究了翻转课堂理念下中职数学教学中混合式教学模式的应用，并利用实例分析了三种混合形式：传统课堂教学、部分翻转课堂教学以及完全翻转课堂教学，希望能为相关人员提供参考借鉴.

【关键词】翻转课堂;混合式教学模式;中职数学教学

一、前言

随着我国教育的不断改革，出现了较多新型的教学方式，混合式教学就是其中的一种.这一教学模式可以将教师的引导、监控以及启发作用充分发挥出来，同时，还会有效提升课堂教学的趣味性，使学生感受到数学学习的乐趣，从而使学生更为积极、主动地参与到课堂学习中.翻转课堂也是一种新型的教学模式，其是利用信息化技术为学生提供更为丰富的学习资源，在课程开始前先让学生进行资源的学习，其本质为“以学生为中心”.基于翻转课堂理念的混合式教学，一方面能够将混合式教学的优势充分发挥出来，另一方面能够实现教学方式的创新，提升学生学习的兴趣.

二、翻转课堂理念下混合式教学模式的构建

（一）传统教学与现代网络多媒体教学的混合

长期以来，我校教育一直采用传统的课堂教学，教师作为知识的传授者，学生作为知识的接受者.这种知识的传授方式较为单一，课堂教学显得枯燥乏味、缺少趣味性，很难使学生积极、主动地参与到课堂教学活动中，也很难得到较好的教学效果，限制了学生创新能力的发展.将多媒体技术及网络化技术引进传统课堂教学中，能够为学生创设出更好的学习环境，丰富课堂教学资源，进一步丰富师生间的沟通方式，可以突显出学生的课堂主体地位，并且还会使教师的主导作用得以充分发挥，使学生实现多样化学习.

（二）传统课堂教学、部分翻转课堂教学和完全翻转课堂教学相混合

这一混合式教学模式是课程教学中实现翻转课堂的一种尝试，其不仅将专业知识教学作为重点，而且强调提升学生的学习兴趣，同时会给学生足够的自主学习时间.在混合式教学中，教师可根据学生特点与课程实际选择最为合适的教学模式.

（三）教师教学活动和学生学习活动相混合

新时期教学理念下，教师与学生在课堂教学中的地位同等重要，但更为重视学生学习的主动性以及自主性，教学活动也是以学生的发展为主要目的.新型教学模式下，教师的教学活动和学生的学习活动如下表所示.

教师的教学活动和学生的学习活动

教师活动[]课堂讲授、准备和发布学习任务和资源、教师点评、组织讨论、解答疑难、批改作业、与学生互动交流、补充讲解

学生活动[]课堂听讲、基于资源开展自学活动、完成个人作业或小组作业、课题汇报、提问讨论、互动交流、课外拓展练习

翻转课堂是对以往教学理念及模式的一种颠覆，这一教学模式更为注重课后传授知识，在课堂中主要进行知识的理解与内化.这种教学方式改变了教师教学、学生学习的秩序及组合，将学生作为了课堂学习的主体，这使得学生的认知模式、学习方式，教师的教学模式，教师和学生的角色都发生了深刻的变化.因此，教师进行评价时要选择多元化的评价方式，要有形成性的评价，还要有总结性的评价，不过，重点还是要放在形成性评价上.

（四）形成性评价与总结性评价有机结合

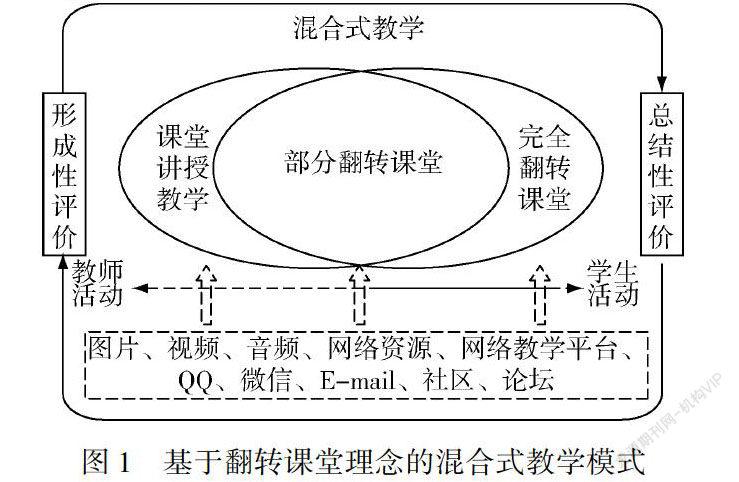
这一教学模式不仅仅局限在课堂教学上，其更为关注的是学生的合作学习及自主学习，并且还将学生的交际能力及资讯素养的培养作为重点.因此，课程评价方式应更为多样，应将多种评价方式结合起来.形成性评价活动应包括成绩展示、学习质量及效果、学生出勤、沟通讨论、日常工作等.而总结性评价活动主要是通过期末考试的方式来评估学生的学习情况，进而判断学生的成绩是否与教学目标要求相符合.在上述分析的基础上，笔者提出了一个基于翻转课堂的混合教学模式，如图1所示.

三、混合式教学模式下中职数学课程的设计

（一）案例一：三角函数

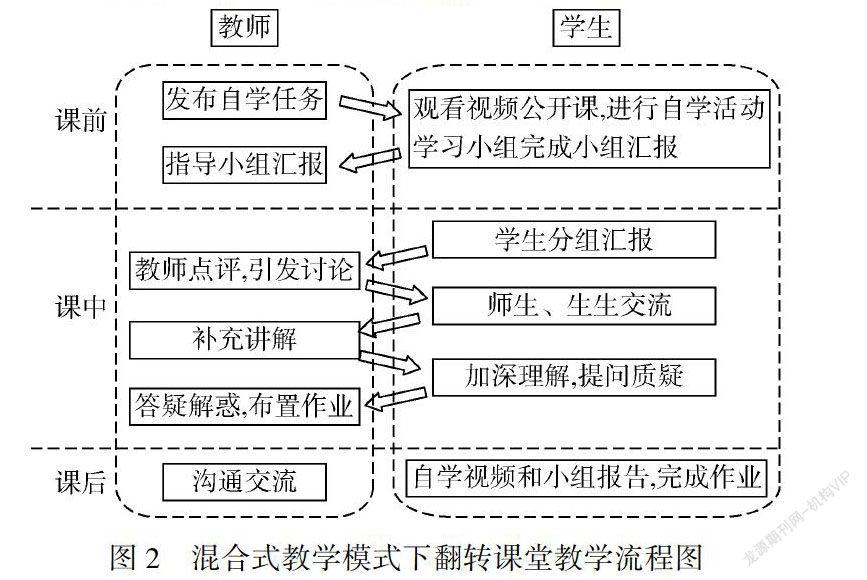
中职数学三角函数的教学流程如图2所示.

1.创设情景 兴趣导入.

引导语：我们知道，现实世界中存在着各种各样的“周而复始”的变化现象，圆周运动就是这类现象的代表.如图3所示，⊙O上的点P以A为起点按逆时针方向旋转.在把角的范围推广到任意角后，我们可以借助角α的大小变化来刻画点P的位置变化.又由弧度制的定义知，角α的大小与⊙O的半径无关，因此，我们可以先研究单位圆上点的运动，即现在的任务是：

如图3，单位圆O上的点P以A为起点在圆上按逆时针方向旋转，建立一个函数模型，刻画点P的位置变化情况.

问题1：根据已有的研究函数的经验，你认为我们可以按怎样的路径研究上述问题？

师生活动：学生在独立思考的基础上进行交流，通过讨论后得出研究路径是：明确研究背景—对应关系的特点分析—下定义—研究性质.

设计意图：明确研究的内容、过程和基本方法，为开展具体研究指明方向.

2.分析具体事例，归纳共同特征.

图4引导语：下面我们利用平面直角坐标系来研究上述问题.如图4所示，一个圆的圆心为O，将其规定为原点，OA为x轴的正半轴，建立平面直角坐标系，已知点A与点P的坐标分别为（1，0），（x，y），OA從x轴的正半轴开始，按逆时针方向旋转α度，最终到达OP位置处.

问题2：当α=π6时，点P的坐标是什么？当α=π2或2π3时，点P的坐标又是什么？它们是唯一确定的吗？

一般地，任意给定一个角α，其终边OP与单位圆的交点P的坐标能唯一确定吗？

师生活动：在学生求出点P的坐标后，追问以下问题：

（1）求点P的坐标要用到什么知识？（斜角三角函数的知识）

（2）求点P的坐标的步骤是什么？点P的坐标唯一确定吗？画出π6角的终边OP，过点P作x轴的垂线交x轴于点M，在Rt△OMP中，利用锐角三角函数可得点P的坐标是32，12，点P的坐标唯一确定.