生鲜品多中心区域协作半开放式配送路径研究

2021-08-04何满辉曹腾马长城

科技促进发展 2021年4期

■ 何满辉曹腾马长城

辽宁工程技术大学工商管理学院葫芦岛市 125000

0 引言

随着第“四次工业革命”的开展，推动了消费转型与”互联网+“时代的到来，生鲜物流业进一步蓬勃发展，但生鲜配送仍有诸多问题亟待解决。生鲜品由于时效性和高品质要求，需要一套合理的配送方案。然而各配送部门各区域内独自配送方案割裂了整体联系，难以实现资源整合，造成资源浪费。同时，由于各配送部门信息技术水平的差异，难以实现信息共享，部门间很难建立合作关系。因此，要树立一种基于信息技术应用，进行区域协同发展，满足顾客要求、整合区域资源，以实现配送高效低成本的新物流发展理念[1-2]。

自车辆路径问题(VRP)提出以来，诸多学者就将智能算法的发展成果应用于物流配送上，以寻求最优的配送路径[3-6]。由于客户需求量的逐年提升，单中心已不能满足实际需求，对多中心车辆路径问题（MDVRP）研究成为热点。葛显龙[7]等在城市供应链多方协同运作背景下，利用改进遗传算法解决设计的模型并验证了带越货配送方案的优越性。鲁建厦[8]等将不同配送中心存在配送费用差异问题考虑在内，通过改进变邻域搜索算法解决相应模型并得出合理的配送调度方案。Petr Stodola[9]等利用蚁群优化算法对MDVRP模型提出一种新的解决办法，具有一定的参考价值。此外,在MDVRP基础上,把时间窗（Time Windows）限制考虑在内,使模型更加实际化，建立了带时间窗的多中心车辆路径问题（MD‐VRTW）。刘玺[10]在物流协同网络下，利用遗传算法解决多车辆配送路径最小成本方案选择问题。

通过进一步研究，考虑车辆与车场关系，提出新的路径模型，即开放式车辆路径问题（OVRP）,该路径区别于封闭式路径，车辆完成任务后可直接驶离，不需要返回车场，若要返回，则需原路径返回。庞燕[12]等在家具制造业将配送环节外包给第三方配送企业趋势下，利用改进的禁忌搜索算法解决OVRP 模型，通过对比实验得出第三方物流配送相对于自营物流能更加节约支出。针对OVRP，Z. Fu 等[13]设计禁忌搜索算法解决该难题，并取得理想的结果。为了解决OVRP，D.Sariklis等[14]提出了一种基于带惩罚程序的最小生成树的启发式算法。

综合上述研究，一方面，以往学者多数对封闭式和开放式路径进行研究，而这两种模式难以符合实际配送要求。MDVRP模型是封闭式的，难以资源融合。OVRP模型多是利用外包资源，难以形成配送标准化。另一方面，解决模型的算法都是仅针对自身改进，存在一定局限性。因此，结合MDVRP与OVRP特点，建立区域协作下带时间窗的半开放式车辆路径模型（HOMDVRPTW）,该模型的车辆路径在完成任务后，不必返回原配送中心，而是依据情况选择合适的车场返回，既改进VRP 模型，车辆不必一定返回原配送中心，减少资源不必要的浪费弊端。又改善OVRP 模型配送难以实现标准化和长期发展的不足。此外，在设计解决此模型算法时，对遗传算法自身改进的同时，与变邻域搜索算法相结合，取长补短，提高算法的性能。

HOMDVRTWP 模型一方面能够反映新物流下区域协作的理念，另一方面在关注配送系统价值同时也关注各配送部门间的资源、信息的共享。随着新物流理念的加深，对于生鲜配送业而言这种模式将是未来发展的趋势。通过对该模式的研究进而可以为未来生鲜企业区域配送发展提出具有借鉴性的意见。

1 问题描述与前提假设

1.1 问题描述

区域协作下的生鲜配送模式，设定在企业配送部门之间接受新物流理念的背景下。问题描述为：A 生鲜企业服务多个区域，每区域内都有一个配送部门，根据历史数据，多区域内建立N 个客户需求点。每个配送部门有D 辆配送冷藏车；冷藏车从配送中心出发，向需求点配送生鲜产品，完成配送任务后，根据情况可以返回任意的配送中心。为提高企业服务水平，配送中心为顾客预先处理生鲜产品；利用信息设备，实时监控车辆位置和冷库温度并在生鲜产品上贴条形码，便于信息及时反馈和数据在部门间实时共享；配送有时间窗限制，超过范围不但会影响生鲜品质量还将受到一定惩罚同时满意度会受到影响；基于上述描述，建立一个生鲜配送成本最小化的模型，同时将时间惩罚、满意度指标考虑在内，尽量减少路径距离，提高设备利用率，从而减少成本，提高满意度。

1.2 前提假设

问题满足以下条件假设：（1）各配送部门的设备规格参数一致，并且有足够的设备能够完成任务；（2）需求点以及配送中心地理位置已知，且坐标固定不变。（3）需求点的需求量不会超过冷藏车车载上限。（4）冷库内外温度稳定不变。（5）每个需求点由一车负责并且只接受一次服务。（6）冷藏车完成任务后离开需求点。（7）冷藏车从任意配送部门开始任务，完成顾客需求生鲜品配送后，考虑较优方案，选择合理的路径返回配送中心。（8）不考虑道路状况，驾驶员以同一速度行驶车辆。

2 模型构建

2.1 符号解释

建立模型的需要，设置了如下符号并予以解释见表1：

表1 符号解释

2.2 满意度函数构建

顾客满意度可以充分体现企业的服务质量，高满意度能提高企业市场占有率。顾客满意度与送达时间成一定的关系，在期望时间内顾客的满意度极高，在可接受的时间范围内随时间的变化会产生改变，超过可接受范围，顾客满意度极低。顾客满意度的函数可以用模糊隶属函数如下所示：

2.3 成本分析

2.3.1 行驶成本

各种行驶损耗，与行驶里程成正相关，表示为（a）：

2.3.2 派遣成本

车辆管理费、驾驶员薪资以及信息设备启动等，与车量成正相关，表示为（b）：

2.3.3 非对称软时间窗惩罚成本

鉴于生鲜产品特性，建立一种非对称性软时间窗。如果在指定时间到达，不会受到惩罚。若提前或者延迟送达会产生惩罚成本，延迟比提前的惩罚更高，如下所示：

时间惩罚成本，表示为（c）：

2.3.4 配送过程中的生鲜货损成本

生鲜产品在配送过程中会发生一定程度的变质，变质的程度受商品本身的特性、时间影响造，生鲜货损系数[14]如下所示：

生鲜货损成本，表示为（d）：

2.3.5 配送过程中的能耗成本

配送过程中由于外部温度对内部的热传递和打开车门作业时热空气侵入导致制冷剂消耗能耗成本表示为：

（1）路途中能耗成本，如下所示：

（2）作业过程中的能耗成本，如下所示：

总能耗成本，表示为（e）：

2.3.6 信息和生鲜处理成本

数据录入、分析和共享及对生鲜品进行预处理，与需求数量正相关：

（1）信息处理成本：

（2）生鲜产品处理成本：

处理总成本,表示为（f）：

2.4 模型建立

基于上述成本分析，模型建立如下：

2.5 模型约束条件

模型建立需加入一约束些条件，以符合论文提出模型特点和要求：

其中（g）生鲜配送最小成本模型；（h）不超过冷藏车装载上限；（i）配送中心对需求点只配送一次；（j）禁止从配送中心出发不经过需求点而直接去配送中心；（k）服务完需求点后不能停留在原地；（l）从配送中心出发，满足需求点后，可返回任一中心；（m）按照顺序执行配送；（n）冷藏车d 将产品送到需求点j 时间;（o）平均满意度必须大于等于百分之七十五：（p）(q)表示（0,1）变量。

3 研究方法设计

3.1 变邻域自适应遗传算法

遗传算法（GA）的优越性在于对大型的复杂问题具有全局搜索最优解的能力,是求解复杂问题的优秀方法。然而，遗传算法不可回避的问题是局部搜索能力和收敛性较差、易“早熟”。变邻域搜索算法（VNS）是对邻域结构进行改变来实现拓展搜索能力以求得较优解的算法。不可忽略的是，初始解的质量直接影响VNS求得最优解的质量。因此，基于遗传算法与变邻域搜索算法的优劣性，将二者进行结合，基于此基础上，设计一种混合算法AGAVNS。该算法拥有全局搜索能力的同时，又避免计算陷入局部最优的困境。AGA 为VNS 奠定了高质量的初始解，而VNS 引导AGA 跳出局部最优，使所求目标解的质量得到一定的提高。

AGAVNS在解决HOMDVRP模型时设计如下：

3.1.1 编码与解码

（1）编码：

算法采用多层编码方式，保证配送问题解的全面性。

第一层编码表示需求点的顺序，编码长度为节点数量N，

第二层编码表示需求点由哪个配送中心发出的车辆进行服务，编码长度为节点数量N，编码为1～K，K 为配送中心数量

如，10需求点，2个配送中心

第一层

第二层

（2）解码：

对应配送中心k，根据第二层编码确定，配送中心k服务的需求点的编号，然后根据第一层编码确定需求点的服务顺序.

如，上例中：

中心1对应需求点和配送次序

中心2对应需求点及配送次序

根据需求点需求及车载上线在上述路径中插入配送中心0

中心1对应需求点及配送次序

0为中心，根据上一个点到所有中心的距离就近选择中心

上述路径可解码为

从中心1出发就近回中心1

从中心1出发就近回中心2

根据该路径，计算各目标函数值.

3.1 2 初始化种群

基本遗传算法初始群的产生一般是随机的，这样会对算法的运算效率和解的质量产生一定的影响。本文利用扫描法生成初始种群。一、建立一个坐标系，以配送中心为原点，将配送中心与任一需求点相连，定义角度，设立需求点坐标。二、从小角度开始，建立一个群组，按逆时针方向把剩余需求量添加到种群中，添加的需求量不能超过冷藏车最大载重量。以此类推，建立新群组，直到所有需求点全部被覆盖。三、这样会得出一个较合理的线路。进行扫描后的初始种群对提高运算的效率和质量有一定的帮助。

3.1 3 适应度评价

通过将带时间窗的多中心半开放式路径问题进行数学模型化，其最终要求是求得配送的最优成本，即求目标函数的最小值。总配送成本为C，适应度值表示为f=1/c，由于配送成本与适应度值成反比，总成本越大适应度越低，个体适用度值越大，越能表明该个体越接近问题的可行解。

3.1 4 选择

轮盘赌是基本遗传算法选择方法，适应度较大的个体被选中的概率也大，反之则小。轮盘赌方法，虽然保证了种群的多样性，但是其随机性可能导致大概率事件依旧可能不发生。因此本文采用轮盘赌与最佳个体保留法相结合方法。一方面保证适应度较高的个体不被破坏能遗传到下一代。另一方面，又克服最佳个体充满空间，陷入局部最优解的弊端。

3.1 5 交叉、变异

基本遗传算法的交叉、变异概率是固定不变。这会对种群的多样性和算法效率造成一定的影响。对于优良个体，应减少交叉变异概率使其能保留；对于不良个体，则加大交叉变异概率使其进化。同时，迭代初期种群需要较高交叉变异概率，快速寻求最优解；后期需要减少交叉变异概率，使找到最优解后快速收敛。因此固定取值不合理，需采用自适应交叉变异概率，按照上述思想进行动态调节。采用自适应交叉、变异概率如下所示：

其中pa交叉概率、pb变异概率、Pcmax交叉概率最大值、Pcmin交叉概率最小值、Pmmax变异概率最大值、Pmmin变异概率最小值、G迭代数最大值、g遗传代数。

算法采用多层编码方式，每一层编码独立进行交叉变异。

①交叉

第一层采用部分匹配。

选择

交换

冲突检测，以4-2-8映射关系为例。

第二层采用单点交叉。

为随机生成交叉点产生新个体

②变异

第一层采用翻转变异

对片段

翻转为

变异后染色体为

第二层采用差值变异

对片段

操作，变异为2（这个2是配送中心数量）加1 减去

等于

3.1.6 变邻域搜索

将遗传算法求得的最优解作为变邻域算法初始解。搜索方法为首先对每代个体的最优解进行变邻域搜索，若在该邻域不能找到一个比当前结果更优的解的时候，则跳入下一个邻域继续寻找。当在本邻域搜寻到一个比现在解更优的解的同时，就跳回第一个邻域重新开始搜索。直到所有邻域都被搜索完毕。邻域结构则采用交换操作，例如

操作前

操作后

3.2 算法流程

根据上述设计，算法流程如图1所示：首先设置基本参数，利用扫描法生成初始化种群，计算适应度，接着运用轮盘赌和最佳个体保留相结合方法进行选择，进行自适应交叉、变异，然后对每代最优解进行变邻域搜索。当程序循环次数达到设定数量时，算法停止。

图1 算法流程图

4 实例分析

4.1 数据来源

以A 生鲜配送企业为例，它服务于三个区域，每个区域都各有一个配送部门，各部门有一个配送中心，为各自区域进行生鲜配送。根据报表，随机选取一天的顾客日需求量，依照历史数据，调查出顾客可接受和期望服务时间，并将需求点位置以1∶5000 缩小在坐标系中。配送中心用A、B、C表示，需求点用数字表示，如表2：

表2 配送中心和需求点数据

4.2 参数设置

采用载重量0.3 吨的冷藏车，冷藏车派遣成本500元，平均速度35 千米/小时，单位行驶成本5 元。采用软时间窗，提前到达惩罚成本为60 元/小时，延迟到达惩罚成本为100 元/小时。冷藏车制冷剂单价0.4 元/千克，车厢内外温差为10 摄氏度。车厢传热面积为12 平方米，常数取值为0.6，传热系数为0.3 千米/（千克*小时）。生鲜产品的价格5000元/吨，产品保质期为14小时，时间敏感调节因子为0.6，作业时间0.25 小时。生鲜和信息处理成本为0.2元/千克和0.4元/千克。

4.3 实验结果分析

利用MATLAB 进行仿真实验,算法参数设置为：NP=100,maxgen=1000,Pamax=0.8，Pamin=0.2，Pbmax=0.5，Pbmin=0.1，Kmax=20,Lmax=50.多次进行实验，并随机抽取8 次实验数据，并选取最值，求均值，如表3-4：

由表3-4，可以得出，随机选取8次计算结果中，平均成本11860.609 元，平均满意度平均值87.7%.平均行驶里程653.574 千米。最优解为成本11652.346 元，平均满意度为96.0%，行驶距离为636.420 千米.最劣解成本为11960.128，平均满意度87.7%，行驶里程678.490 千米。最优解、最劣解与平均值的相对偏差分别为0.89%、0.42%，所需冷藏车均为7 辆，运行时间均在22 秒内。因此，混合算法的解能稳定收敛于较优解，且运行时间较快。

表3 区域协作下混合算法随机选取8次计算结果

表4 区域协作下运算结果最优劣解与均值

为证明区域协作下半开放式路径合理性，与A 生鲜企业目前方案对比，该方案利用遗传算法求解最有路径且已用于各区域各部门独立配送，数据为：成本15957.372 元、里程877.73 千米、平均满意度15.4%、冷藏辆8辆，配送方案如表5：

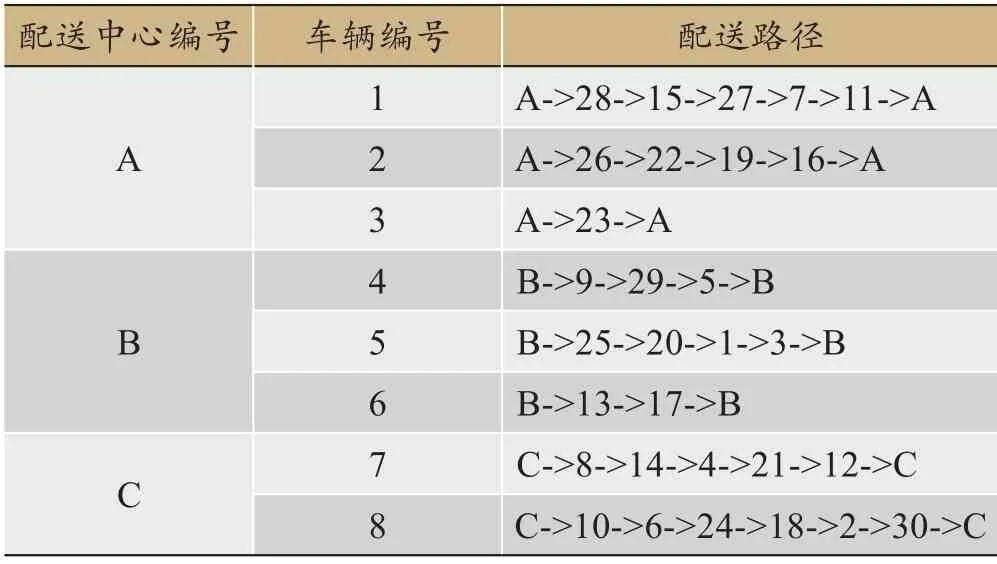
表5 各区域独立配送方案

经过两种模式的对比可知，区域协作下的半开放式配送成本平均值比各区域独立封闭式配送成本下降了25.67%，现配送模式比原来的平均满意度增长了72.30%。同时原里程数较现平均里程数降低了34.30%，车数从8 辆减少到7 辆。整体客户平均满意度超过80%。由此可以得出，区域协作下的半开放式配送路径较各区域独立配送，降低了成本，使企业盈利能力提高；行驶里程降低，提高了配送效率；保证了客户满意度同时使车辆的利用率提升，也考虑了信息共享和客户服务，能促进整体生鲜配送的合作发展。因此，此模型是合理的、有效的。

根据以上数据，可知第三次实验效果最佳，其方案如表6。同时利用基本遗传算法对区域协作下的半开放式模型求解，得出数据：成本12301.338 元、里程740.96千米、平均满意度81.9%、冷藏车7 辆。混合算法较遗传算法成本下降了5.3%、里程下降了14.1%，平均满意度提升14.1%。根据以上所有数据和算法对比迭代图（图2）可知，AGAVNS较基GA能够跳出局部最优解，提高解的质量并且收敛性更稳定。因此AGAVNS 较GA 在解决该模型上具有一定的改进。

表6 区域协作下配送最优方案

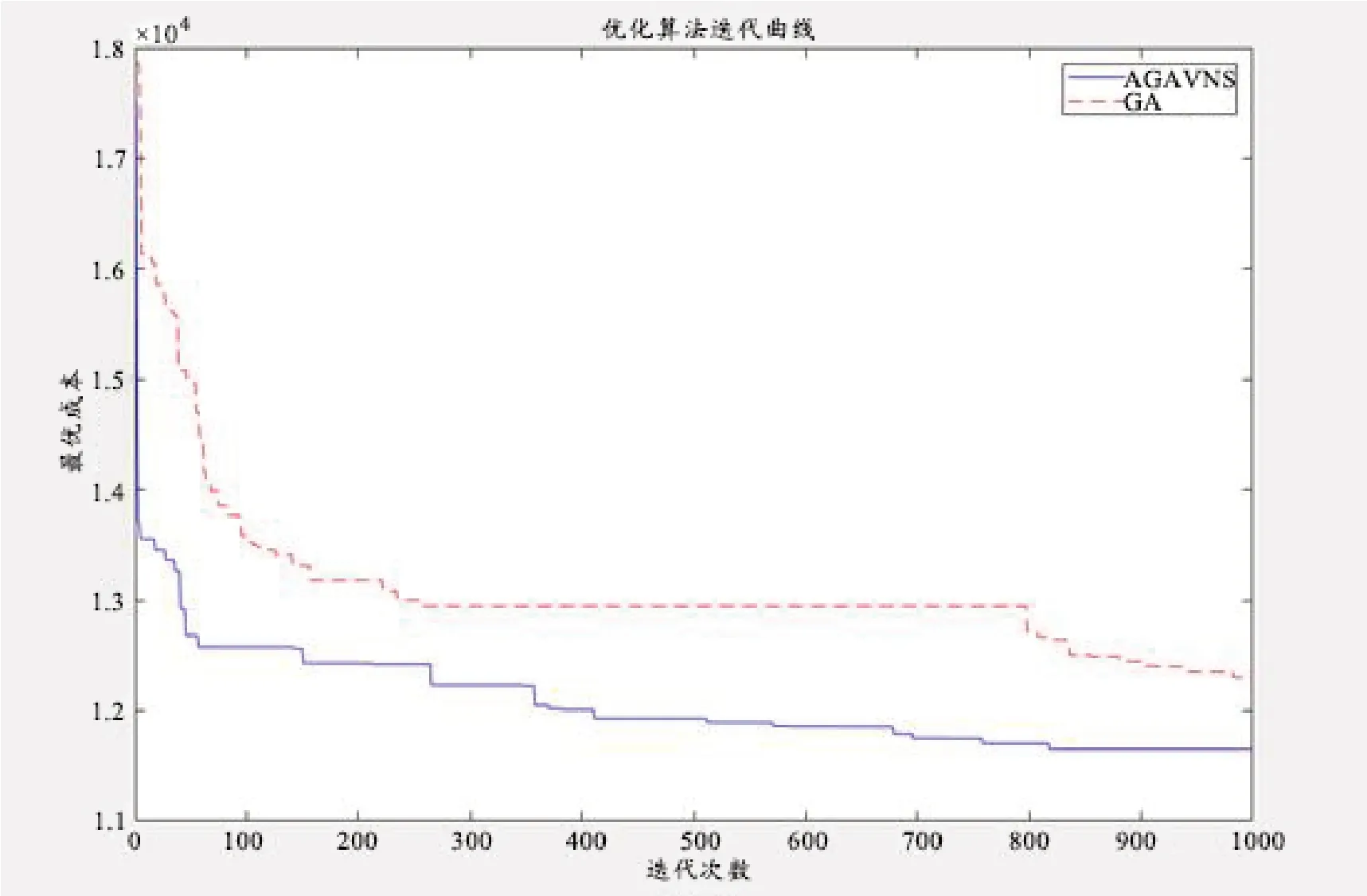
图2 算法迭代图对比

5 结语和对策建议

本文以区域生鲜企业配送过程为研究对象，提出各配送部门各区域独立配送造成严重资源浪费、高成本、低满意度的弊端。在新物流理念下，设计了区域协作下的多中心半开放式配送模式，并建立考虑时间窗和保持一定客户满意度约束下的成本优化模型，应用AGAVNS多次求解。结合A 生鲜配送企业数据，模型通过与各区域独立配送方案比对，以及AGAVNS 与GA 对比，验证了模型合理性和算法改进性。研究成果可以有效降低生鲜企业配送的成本，降低客户投诉率，加快运作效率，为促进区域生鲜物流的协作发展提供一定参考。

同时，基于研究成果，对未来生鲜配送企业进一步发展提出对策建议：