钢-混组合梁负弯矩区抗阻裂设计探析

郭 君

(福州市规划设计研究院集团有限公司 福建福州 350108)

0 引言

在现代桥梁工程中，继钢筋混凝土结构、预应力混凝土结构、钢结构以及砖石混凝土结构之后，钢-混凝土组合结构已成为第五大类结构。钢-混凝土组合梁是由外露的钢梁或钢桁梁通过连接件(剪力键)与钢筋混凝土板组合而成的结构[1]。

钢-混凝土组合梁利用钢材的抗拉性能、混凝土的抗压性能，能充分发挥技术、经济效益。相对不按组合结构设计的纯钢梁，组合梁可以有效减小结构高度、提高结构刚度、减小结构在活荷载下的挠度[2]。

对于简支梁而言，位于钢梁上部的混凝土板兼作桥面板，主要承担由弯矩引起的纵向压应力，下部的钢梁则主要承受拉应力[1]。

对于连续梁，中支点区域的负弯矩在混凝土板内产生拉应力，钢梁内产生压应力，钢梁受压的稳定性通过钢梁压应力限值及构造措施加以保证。负弯矩区混凝土面板的抗阻裂性能，则是控制组合梁受力性能的关键部位。

1 负弯矩区抗阻裂措施

根据《建筑结构可靠性设计统一标准》(GB 50068-2018)，当采用结构的作用效应和结构的抗力作为综合基本变量时，结构按极限状态设计应符合下列规定[3]：

R-S≥0

式中，R——结构的抗力；

S——结构的作用效应。

由上述功能函数可知，为改善负弯矩区混凝土板的抗裂性能，可采取减小内力和增大抗力两方面的措施。减小内力可采用：①合理选择构件尺寸、降低结构恒载；②分节段浇筑桥面板、减小中支点区域负弯矩值。增大抗力可采用：①采用高性能混凝土或者微膨胀钢纤维混凝土，也可在混凝土中添加聚丙烯纤维，以提高抗裂性；②张拉桥面板负弯矩区预应力钢束；③支点强迫位移法[4]。不同的方式对组合梁内力及桥面板应力、裂缝的发展有不同影响。

2 数值分析

某工程为城市主干道，主线左右幅共布置有6联钢-混组合梁，左幅跨径布置分别为(3×30)m、(32+43+43.5)m、(4×37)m，右幅跨径布置分别为(3×30)m、(32+42+42)m、(4×37)m。单幅桥面宽度为12 m，采用双箱单室截面，单室宽度为3.0 m，悬臂宽度2.0 m。桥梁结构中心线处梁高为2.1 m，其中混凝土桥面板厚0.34 m，桥面横坡通过腹板变高形成。横向加劲肋间距为2.0 m，横隔板间距为6.0 m(支点附近加密为3.0 m)。桥梁特征断面如图1所示。本文选取(32+43+43.5)m联组合梁进行计算分析。

(a)横向加劲处桥梁断面

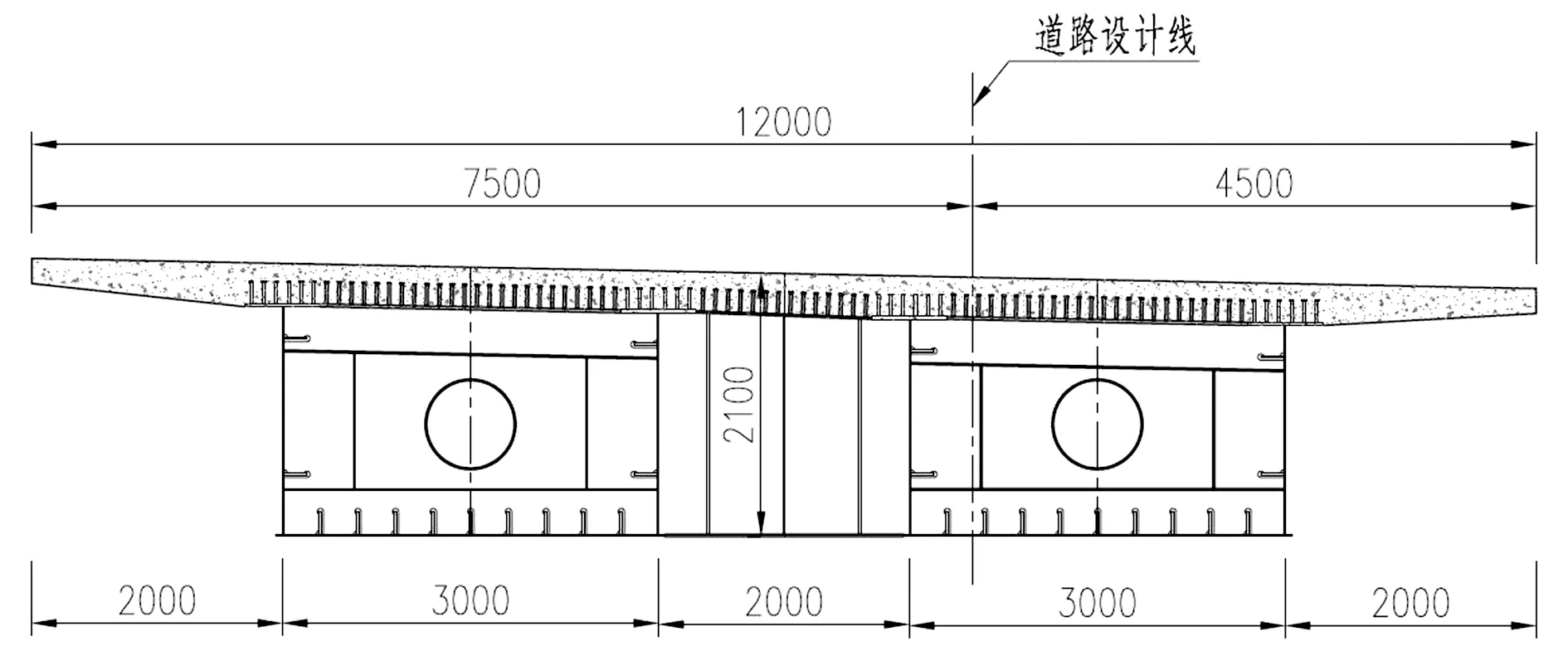
(b)横隔板处桥梁断面图1 桥梁特征断面(单位：mm)

2.1 理论分析

钢主梁腹板高厚比大，截面抗弯承载力计算采用弹性设计方法。计算时应计入施工顺序，以及混凝土的徐变、收缩与温度等作用的影响[5]。

(1)内力及强度计算

根据结构设计原理，按照平截面假定，组合截面在弯矩作用下产生的应变如图2所示。

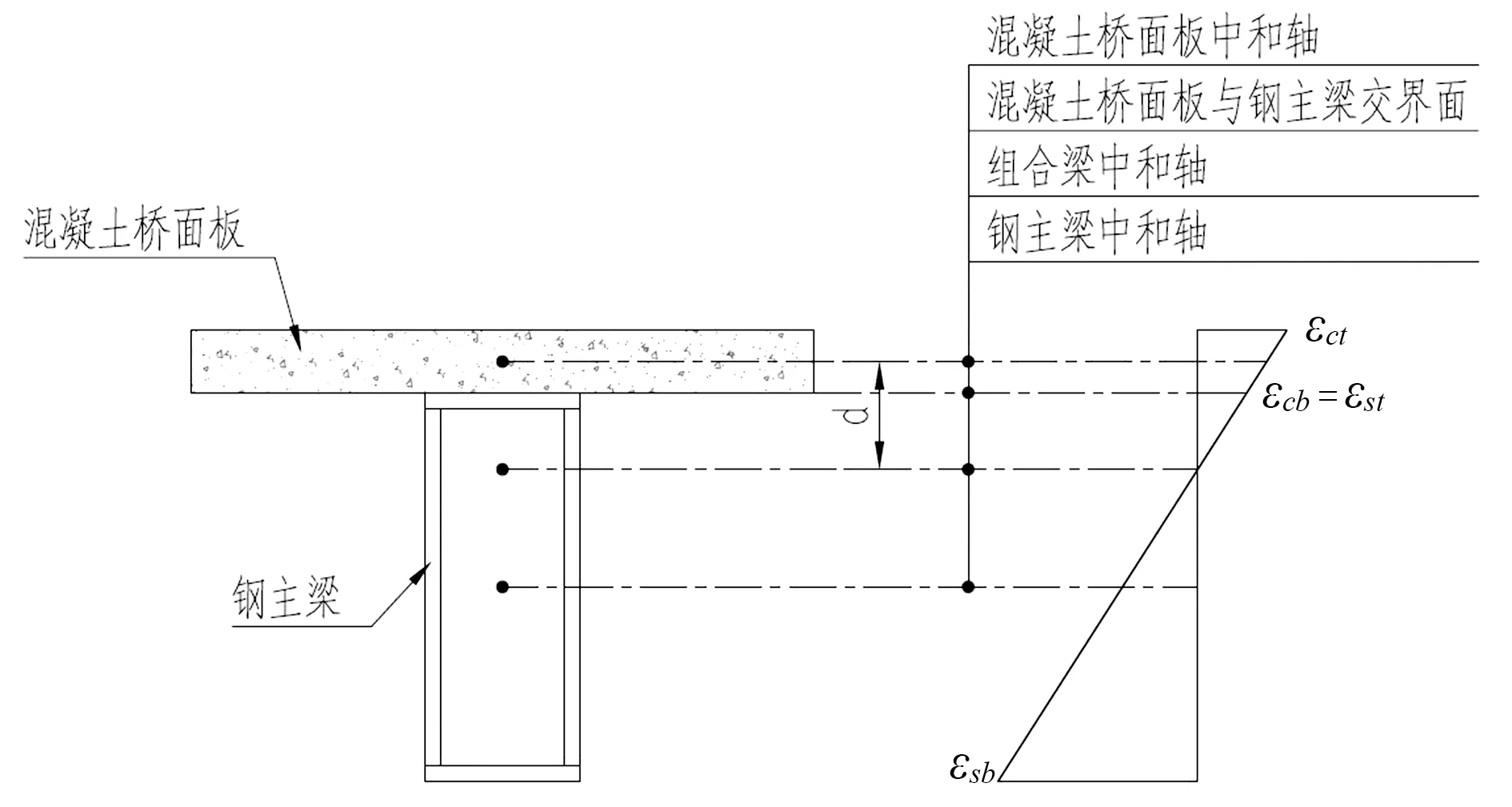
图2 弯矩作用下组合梁截面应变示意图

桥面板应变由轴向应力引起的应变和弯曲应力引起的应变叠加而成，如图3所示。

图3 弯矩作用下桥面板截面应力示意图

图中应力通过以下公式计算：

σct=Ec·εct

(1)

σcb=Ec·εcb

(2)

(3)

σcft=σct-σca

(4)

σcfb=σcb-σca

(5)

混凝土桥面板内力由应力计算得到，计算公式如下：

Fcx=Ac×σca

(6)

(7)

式中，εct、εcb、εst、εsb——桥面板顶缘及底缘、钢主梁顶缘及底缘应变；σct、σcb——桥面板顶部及底部应力；σca——桥面板由轴向力引起的均布应力；σcft、σcfb——桥面板由弯矩引起的顶缘、底缘应力；Fcx、Myc——桥面板子截面轴力、弯矩；My——组合截面的总弯矩；Ac——桥面板截面积；Icyy、Isyy——桥面板、钢主梁对y轴的惯性矩；n——钢材与混凝土弹性模量比，整体分析可采用长期弹性模量比。

组合梁抗弯承载力，以组合梁截面任意一点的应力达到材料强度设计值，作为抗弯承载力的标志。

(2)裂缝计算

组合梁负弯矩区桥面板处于受拉状态，是裂缝发展的控制位置，其受力行为接近于混凝土轴心受拉构件。对于钢筋混凝土板，作用(或荷载)短期效应组合引起的开裂截面纵向受拉钢筋的应力σss可按式(8)计算[6]：

(8)

将上式计算得到的钢筋应力代替混凝土轴心受拉构件的钢筋应力值，按混凝土轴心受拉构件，计算负弯矩区组合梁桥面板最大裂缝宽度。

2.2 计算参数

(1)梯度温度

基于组合梁的截面特点，对温度梯度作用进行细分。本工程桥面铺装采用8cm厚沥青层，竖向日照正温差计算的温度基数按照厚度内插，得T1=16.4°C，T2=6.0°C。沿截面竖向温度梯度划分如图4所示。

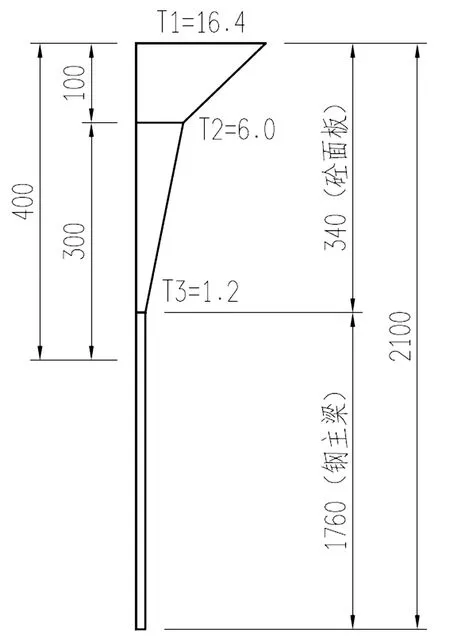
图4 截面竖向梯度温度示意图(单位：mm)

对应各梯度温度特征位置，参数如表1所示。

表1 截面竖向正温差梯度温度参数

混凝土桥面板范围内考虑温度梯度作用，钢主梁段按照均匀温度考虑。

(2)截面刚度的选取

结合不同抗阻裂方式及不同区域的工作状态，采用合理的截面刚度。结构计算采用桥梁博士V4.3.0，采用空间杆系模型。程序中未考虑横向加劲肋、横隔板重量，需通过自重系数进行调整，横向加劲布置对局部稳定折减系数有影响。

截面刚度根据《公路钢混组合桥梁设计与施工规范》(JTG/T D64-01)相关规定选取：

①当混凝土桥面板按全预应力或部分预应力混凝土A类构件设计时，应采用未开裂分析法，组合梁截面刚度，应取未开裂截面刚度。

②当混凝土桥面板按照部分预应力混凝土B类或普通钢筋混凝土构件设计时，应采用开裂分析法。即中支点两侧各0.15L范围内，组合梁截面刚度取开裂截面刚度，其余区段取未开裂截面刚度。混凝土开裂影响范围内，不计负弯矩区混凝土的抗拉贡献，仅计入混凝土板翼缘有效宽度内纵向钢筋的作用[7]。

根据施工工序进行模型的建立，单元总数为65，节点总数为66，模型如图5所示。模型对中支点两侧各0.15L范围内截面刚度分别取开裂和未开裂截面刚度，对内力计算结果进行对比。

图5 组合梁有限元模型

以下计算结果取特征位置列出。下述表格中，D1、D3、D5依次表示各跨跨中位置，D2、D4依次表示中支点位置。

中支点两侧各0.15L范围内截面刚度取开裂截面刚度，内力计算结果如图6所示。

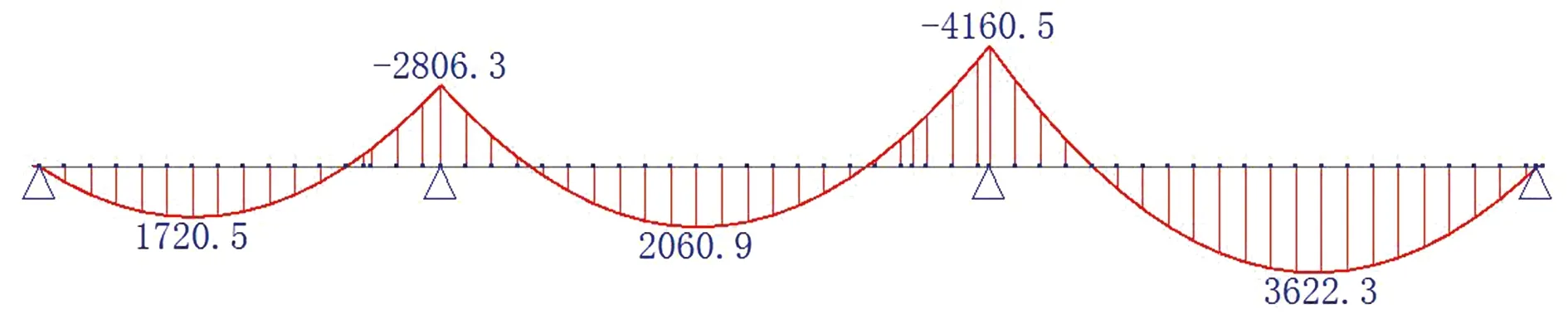
(a)铺装荷载作用下弯矩图

中支点两侧各0.15L范围内截面刚度取未开裂截面刚度，内力计算结果如图7所示。

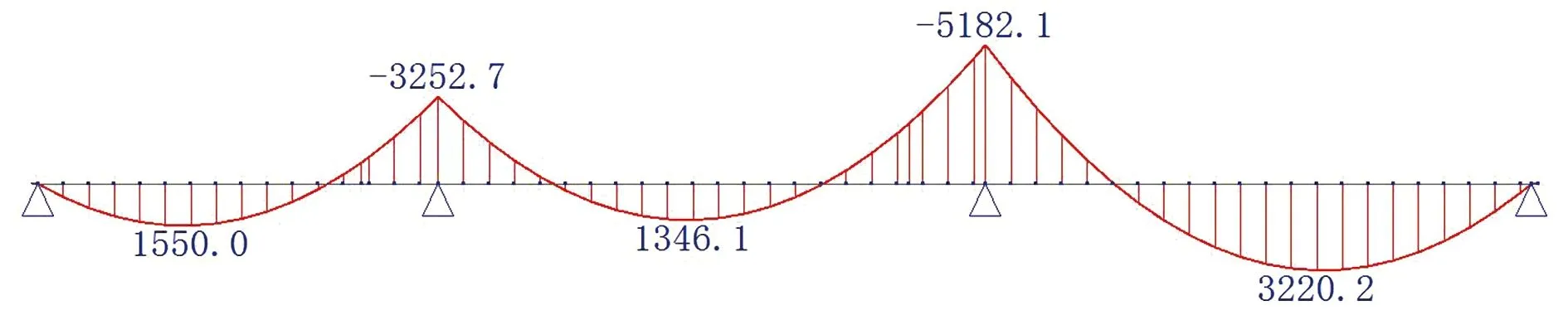
(a)铺装荷载作用下弯矩图

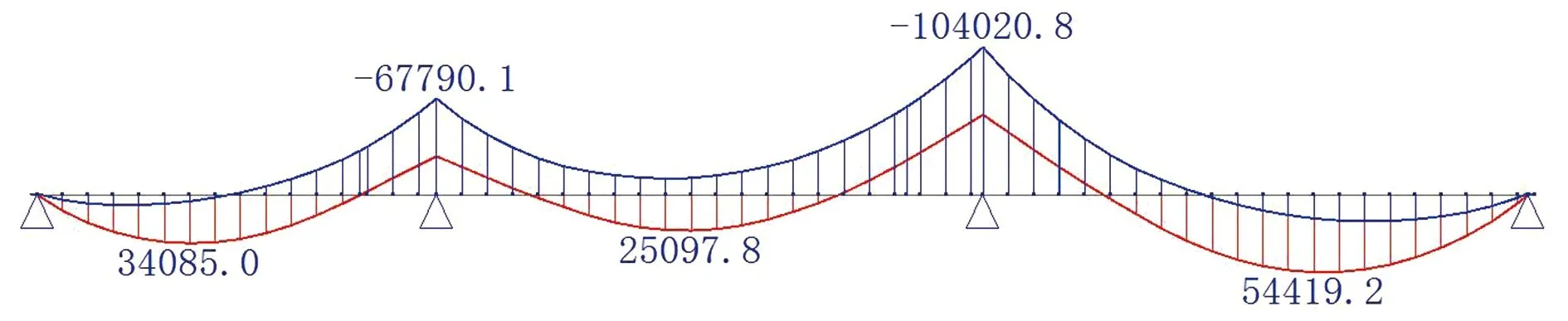
(b)作用基本组合下最大、最小弯矩图图7 取未开裂截面刚度弯矩图(单位：kN·m)

将特征位置弯矩罗列对照，结果如表2～表3所示。

表2 铺装荷载作用下特征截面位置弯矩值(kN·m)

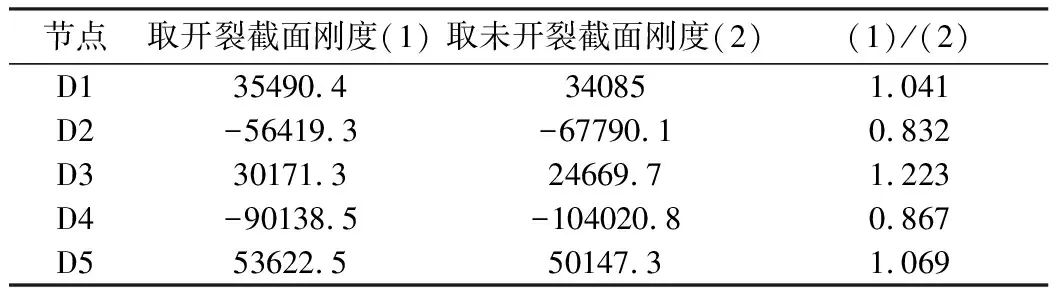
表3 作用基本组合下特征截面位置最大/最小弯矩值(kN·m)

注:上表所述截面刚度均指负弯矩区段0.15L范围内截面刚度；“-”表示负弯矩。

由表2可知：由于中支点两侧各0.15L范围内截面采用开裂截面刚度，与跨中截面刚度比减小，对负弯矩区有一定卸荷效果。在铺装荷载作用下，负弯矩值减小13.7%～19.7%，跨中正弯矩值增大16.7%～52.2%。其中，中跨调整幅度最大，为52.2%。

注:上表所述截面刚度均指负弯矩区段0.15L范围内截面刚度；“-”表示负弯矩。

由表3可知：基本组合下最大负弯矩值减小13.3%～17.8%，跨中正弯矩值增大4.1%～22.3%。其中，中跨调整幅度最大，为22.3%。对比表2可知，作用基本组合下弯矩调整幅度较铺装荷载作用下减小，因为自重引起的弯矩值基本一致。刚度的差异主要影响二期荷载、活载等产生的内力的分配。

基于以上分析，根据不同抗阻裂方式的作用机理，以下分析选取合适的截面特性，计算混凝土桥面板内力、应力及裂缝宽度等指标，对比分析不同抗阻裂措施的技术经济性。

2.3 混凝土桥面板分节段浇筑数值分析

为减小负弯矩区桥面板弯矩，根据连续梁受力特点，采用先浇筑正弯矩区桥面板混凝土，待强度形成后，再浇筑剩余桥面板混凝土，以释放负弯矩区截面的部分变形、减小负弯矩。中支点两侧各6m范围内桥面板混凝土为二期浇筑。

作为对照，建立桥面板一次浇筑成型的模型，对桥面板成桥运营阶段的应力及裂缝宽度进行比较，以分析桥面板分节段浇筑对桥面板受力的影响程度。

由图8可知，桥面板上缘压应力右边跨中区域较左边跨大。考虑负弯矩区桥面板开裂，在中支点附近桥面板上缘应力释放。正应力(压应力)最大差值为0.05MPa，分节段浇筑产生的压应力更大，出现在中跨跨中位置。两种工序的桥面板应力接近，且均满足要求。

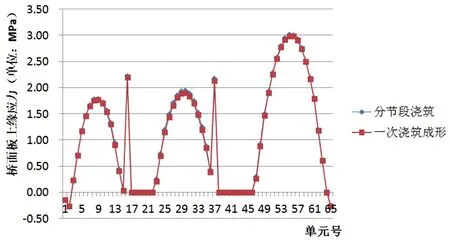
图8 作用基本组合下桥面板上缘应力对照图(单位：MPa)

由图9可知，桥面板上缘最大裂缝宽度出现在中支点附近区域，边跨靠近端支点一定范围无裂缝。分节段浇筑产生的最大裂缝宽度，较一次浇筑成型减小0.004 mm。

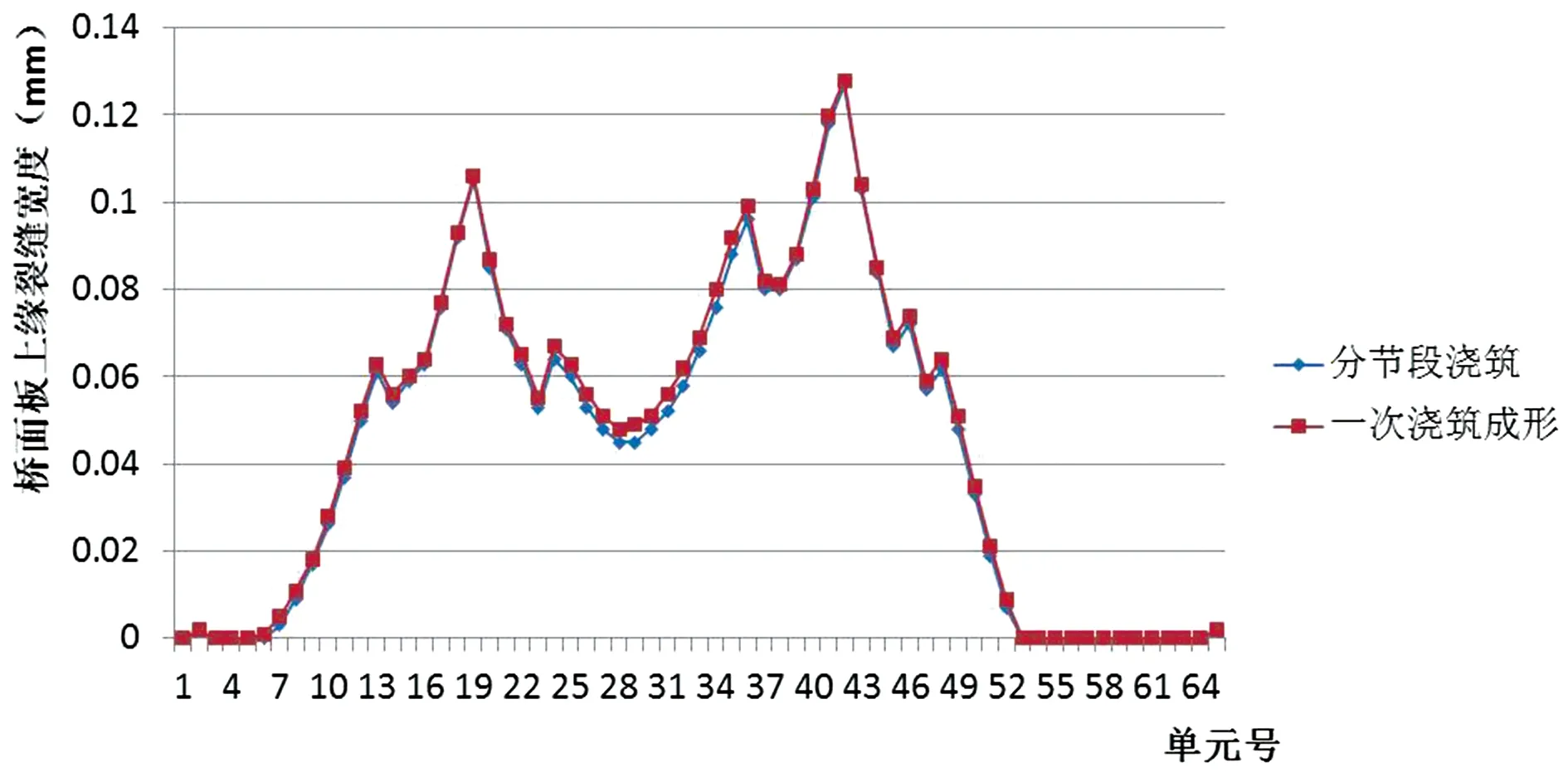
图9 桥面板上缘裂缝宽度对照图(单位：mm)

分析分节段浇筑对桥面板负弯矩区裂缝发展改善有限的原因：一方面，二次浇筑的范围较小(中支点两侧各6m，约为1/7跨径)，产生的负弯矩值有限；另一方面，中支点一定范围内组合梁截面采用开裂刚度，且钢与混凝土刚度比大，桥面板分配所得弯矩值较小。采用预加荷载方式，通过钢主梁强迫弹性变形，可进一步改善桥面板受力。

结合图9，桥面板横向裂缝在中支点两侧各0.15L(L为跨径)范围内较大，横向钢筋在该区域宜加强，以减小局部纵向裂缝，改善该区域桥面板的工作性能。此外，考虑桥面板刚度变化的阶段性，中支点区域桥面板刚度减小有一个发展过程，工程中宜采用分节段浇筑，并采用无收缩混凝土，添加聚丙烯纤维，以尽量减少混凝土硬化过程中产生温度裂缝。

2.4 桥面板布置预应力钢束数值分析

根据组合梁受力特点，桥面板可采用张拉预应力钢束的方式，抵消部分由负弯矩在截面上缘产生的拉应力，以保持桥面板全截面处于受压状态，提高组合梁的耐久性。

以下分析中，钢束拟采用φs15.2高强度低松弛预应力钢绞线，钢束标准强度为1860 MPa，张拉控制应力为0.7fpk=1302 MPa。桥面板厚度为340 mm，钢束规格为15-8，波纹管中心线距离板顶140 mm。钢束采用通长束结合短束的方式，钢束布置于钢主梁箱室范围内，横向间距150 mm，一个箱室布置15根，其中8根为通长束，7根为短束。钢束均采用两端张拉，张拉端设置齿块。通长束张拉端距离梁端2500 mm，短束张拉端距离中支点各10 000 mm，如图10所示。

桥面板按照A类预应力混凝土构件设计，正常使用极限状态下，桥面板拉应力均小于混凝土抗拉强度设计值，桥面板未开裂，中支点两侧各0.15L范围内截面采用未开裂刚度，内力计算结果如图11所示。

(a)桥面板钢束断面图(单位：mm)

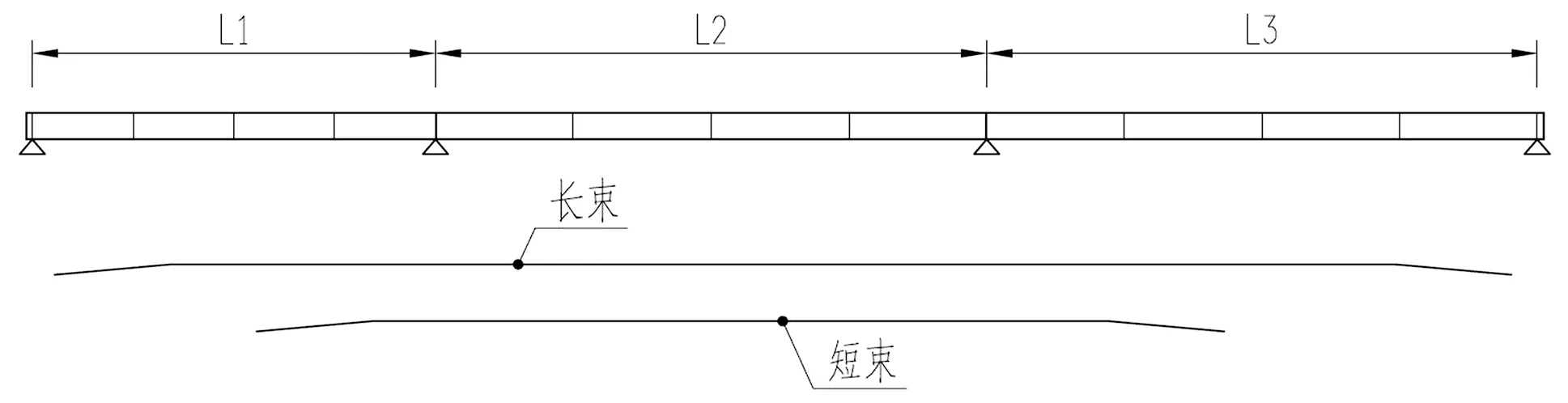
(b)桥面板钢束纵向布置示意图图10 桥面板预应力钢束布置图

对比图6、图11可得：

图11 作用基本组合下组合梁最大最小弯矩图(单位：kN·m)

(1)设置桥面板钢束后，由于负弯矩区截面未开裂且钢束对截面刚度的影响，内力分布有调整。边跨跨中最大弯矩变化幅度小，在4.7%～5.9%之间。

(2)中跨范围内钢束效应最大，跨中最大弯矩大幅减小，跨中范围桥面板全截面均处于受压状态。对于市政工程，由于地下管线、构造物等因素造成的中跨与边跨比偏大情况下，设置桥面板钢束，能取得较好的综合效益。

(3)设置钢束后，中支点范围内最大负弯矩值增大25.8%～40.9%。对于该区域截面，设置钢束后，提高截面抗裂性能的同时，刚度的提高也造成内力增大。

此外，由于预应力波纹管的设置，横向剪力键间的混凝土厚度减小，混凝土对剪力键的握裹作用减弱，滑移效应增大。随着剪力栓钉间距的增大，弹性变形挠度百分比减小，滑移变形挠度百分比变大，并最终趋于稳定[8]。布置预应力钢束对组合梁远期刚度影响程度的量化，有待进一步研究。

张拉桥面板钢束能有效改善桥面板应力，在作用频遇组合下，拉应力(图12)均小于混凝土抗拉强度设计值。

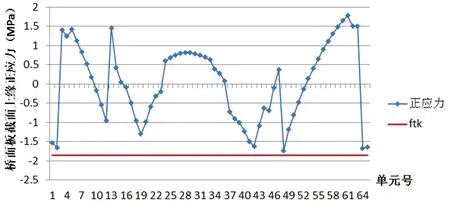
图12 作用频遇组合下截面法向拉应力(单位：MPa)

分析作用基本组合下钢主梁截面上、下缘正应力可知，在钢束引起压应力作用下，中支点区域钢主梁截面上缘、跨中区域近截面下缘拉应力减小，受力改善。中支点区域钢主梁截面下缘、跨中区域截面上缘压应力相应增大。与采用普通钢筋混凝土桥面板的组合梁相比，采用预应力混凝土桥面板的组合梁应结合钢束布置，调整钢主梁板件的厚度设计，以达到合理经济的目的。

3 技术经济比较

以上，对不同抗阻裂方式下组合梁桥面板的内力、裂缝及应力进行了分析。结合经济性、工期、施工难度等各方面因素，对以上两种方式进行综合比较，如表4所示。

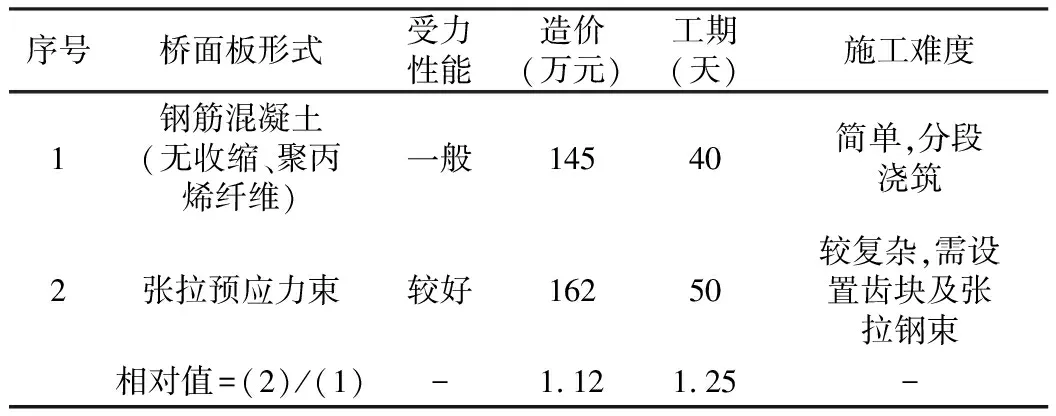
表4 两种抗阻裂方式技术经济比较表

由表4可得，桥面板张拉预应力钢束，全截面未开裂，受力性能改善，但工期增加25%，造价增加12%，且施工较复杂，施工质量较难控制。桥面板采用钢筋混凝土，通过加大主筋来控制裂缝宽度，混凝土采用无收缩混凝土，并添加聚丙烯纤维，可较好地控制裂缝宽度，但桥面板带裂缝工作，耐久性欠佳。工程中若采用钢筋混凝土桥面板，宜适当提高防水等级，并严格把控施工质量。

4 结论

通过对本工程(32+43+43.5)m联钢-混组合梁两种抗阻裂方式的计算分析，即分节段浇筑桥面板、张拉桥面板钢束，得到以下结论：

(1)截面刚度对组合梁内力分布影响大。桥面板按照钢筋混凝土构件设计，中支点两侧各0.15L(L为单跨跨径)范围内采用开裂截面刚度。较该范围采用未开裂截面刚度，作用基本组合下中支点处最大负弯矩减小13.7%～19.7%，跨中弯矩相应有所增大，尤其是中跨。

(2)混凝土桥面板采用分节段浇筑时，二期浇筑的范围对中支点裂缝的改善有一定影响，宜取距中支点各0.25L范围。

(3)以本工程为例，43.5 m边跨对应中支点负弯矩区横向裂缝最大宽度为0.13 mm，该区域桥面板顶层横向钢筋应加强(如双排并置)，减小顶缘纵向裂缝宽度，以控制该区域裂缝的发展。工程实践中，对于跨径小于40 m的结构，可考虑采用分节段浇筑普通钢筋混凝土桥面板，并对该区域钢筋进行加强。

(4)张拉预应力钢束能有效改善桥面板应力，保证在正常使用极限状态下桥面板不开裂。截面刚度增大，同步引起负弯矩值增大。与分节段浇筑普通钢筋混凝土桥面板相比，增大25.8%～40.9%。

(5)通过技术经济性比较，桥面板采用张拉钢束的方式，与采用普通钢筋混凝土桥面板相比，造价增加约12%，施工工期增加约25%。

(6)在使用环境严苛、耐久性要求高或跨径较大(大于40m)的工程，宜优先考虑采用张拉预应力钢束的方式进行抗阻裂设计，可结合采用支点强迫位移法(中支点预先顶升，待桥面板浇筑、强度形成后，梁体回落，达到对桥面板施加压力的效果)。

(7)支点强迫位移法施工工期长、工艺与流程较为复杂，对现场控制要求较高。此外，顶升回落引起的钢主梁与混凝土桥面板的相对滑移、钢束预应力损失等也应充分考虑[4]。

通过理论计算及综合比较，这两种抗阻裂方式各有优劣，在实际工程中可采用两种或多种相结合的方式，保证桥面板的使用性、耐久性。随着高性能混凝土的逐步推广，其良好的力学性能也可作为一种比选方案，在今后工程实践中加以进一步研究论证。