硅酸锂球床传热传质特性与吹扫气体流动的DEM-CFD耦合模拟

张宝锐，夏兆阳，周志伟

(清华大学 核能与新能源技术研究院，北京 100084)

聚变堆包层作为聚变堆的关键部件，承担着氚增殖、能量转换及辐射屏蔽等功能。包层氚增殖剂按其形态可分为固态包层和液态包层，其中固态包层采用锂陶瓷颗粒作为氚增殖材料，球床采用低压氦气作为吹扫气体将氚载出，并掺杂一定量的氢气以加快氚的载带[1-2]。球床的内部结构会对吹扫气体的流动特性及球床内的传热传质行为产生影响，因此获取球床气体的详细流动特性及传热传质特性对包层氚输运分析及氚提取系统设计具有重要意义。

在球床堆积方面，Gong等[3]采用不同尺寸的铝合金颗粒进行了一元及二元尺寸球床的堆积实验，填充率均可达到设计目标。他们同时采用离散单元法(DEM)计算程序进行了数值模拟，填充率和孔隙率分布与实验结果符合得较好。在球床流动阻力特性研究方面，Abou-Sena等[4]基于其设计的压降测量装置，测量了不同填充因子、流速及粒径下的氦气流动压降，验证了Ergun方程的适用性；伍振兴等[5]发现在颗粒粒径较小(低于1 mm)时，Ergun方程预测值低于实验值，通过理论推导得出了考虑氦气可压缩性影响的修正Ergun方程，与实验值符合良好；汪卫华等[6]首先采用计算流体力学(CFD)方法对规则堆积的氚增殖球床进行了数值模拟，获得了球床内的流速及压力分布；Zhang等[7]、陈有华等[8]分别对一元及二元球床进行了DEM-CFD耦合计算，获得了随机堆积球床内的吹扫气体速度及压力分布，发现在壁面处出现流体加速，而在堆积较密实的区域存在流动迟滞区。在球床等效导热系数研究方面，Donne等[9]、Liu等[10]采用稳态热流法分别对不同堆积率下的硅酸锂球床进行了等效导热系数的测量实验，获得了等效导热系数与平均温度的线性拟合关系；骆贝贝等[11]在中国先进研究堆(CARR)中开展了辐照环境下硅酸锂球床等效导热系数的测量，并与理论值和堆外实验拟合值进行了比较。

球床内部结构复杂，为减小计算量，目前针对固态包层模块的热工水力及氚输运分析将氚增殖球床等效为固体域或多孔介质域，因此需获得球床结构下流体流动特性及球床等效导热系数，并对氚在吹扫气体内的扩散系数进行修正。本文以核工业西南物理研究院提出的一种氦冷固态包层概念为研究对象[12]，采用离散单元法生成满足填充率要求的球床随机堆积结构，并对该精细模型开展吹扫气体流动特性研究与球床导热模拟，为后续包层的传热传质多物理场耦合模拟提供宏观输入参数。

1 随机堆积模型与网格划分

1.1 球床随机堆积模型的DEM计算

氦冷固态包层采用粒径为1 mm的硅酸锂颗粒作为氚增殖剂，为模拟真实的球床堆积结构，本文采用DEM对硅酸锂球床的堆积结构进行数值模拟。DEM的基本思想是将每个颗粒看作具有质量、形状、速度等参数的独立单元，基于不同的接触模型，在每个时间步内确定颗粒的接触力，并对颗粒的加速度、速度、位移等参数进行更新，直至球床达到应力平衡状态。计算流程如图1所示。

图1 DEM计算流程Fig.1 Simulation procedure of DEM

DEM计算程序采用PFC3D，所需的硅酸锂颗粒物性参数列于表1[3]。圆柱形球床工业应用广泛，其填充结构也有较成熟的研究，在球床直径与颗粒直径比小于10时，壁面效应会对球床填充率有较大影响[13-15]，因此本研究中设定计算模型为半径6.5 mm、高度9.0 mm的圆柱体，初始时刻在圆柱体顶部生成位置随机的硅酸锂颗粒，随后硅酸锂颗粒在重力作用下落入圆柱体内部，颗粒-颗粒与颗粒-壁面间接触力的确定基于Hertz接触模型[16]。

表1 用于球床堆积模拟的硅酸锂物性参数Table 1 Main parameter of Li4SiO4for DEM simulation

经多次迭代后球床达到应力平衡状态，得到氚增殖球床随机堆积结构，如图2所示。

图2 硅酸锂球床离散堆积模型Fig.2 Structure model of Li4SiO4 pebble bed

球床模型共模拟了1 348个硅酸锂颗粒，总体堆积率为59%，球床内径向孔隙率验证多采用Klerk提出的径向孔隙率分布经验关系式[17]：

(1)

其中：εr为径向孔隙率；R=(r-rc)/d为无量纲距离，r为测点与圆柱体中轴距离(0≤r≤rc)，rc为圆柱体半径，d为颗粒粒径；εb为球床中心平均孔隙率。

模型径向孔隙率分布与Klerk关系式的对比如图3所示。由图3可知，模型径向孔隙率分布与经验值符合良好，可认为DEM计算得到的球床堆积结构真实合理。

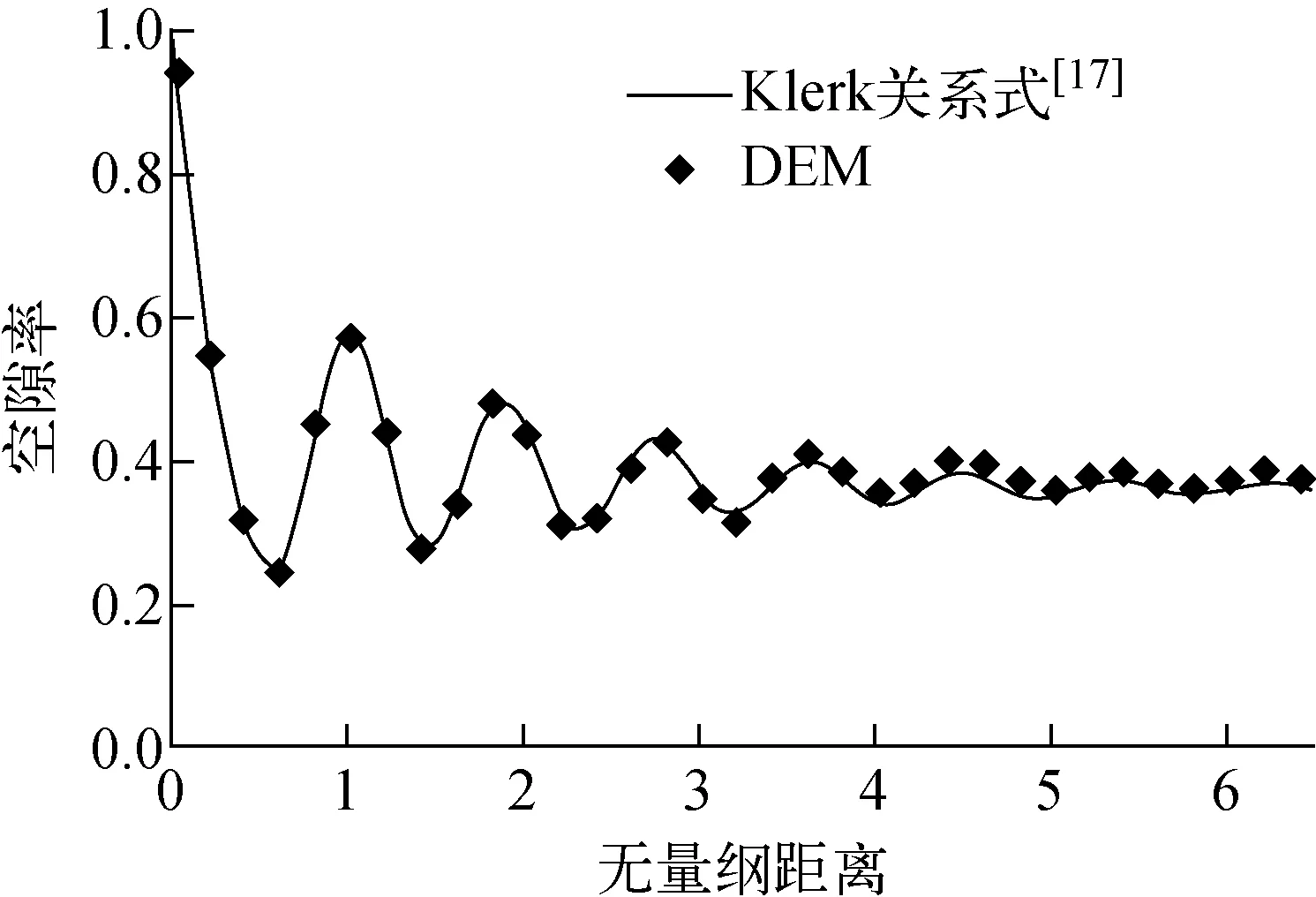
图3 径向孔隙率分布Fig.3 Radial porosity distribution

1.2 CFD模型重建与网格划分

1) CFD模型重建

采用有限元计算软件COMSOL Multiphysics进行氚在球床结构内的等效扩散系数及吹扫气体流动的数值模拟。COMSOL除了可视化建模，其提供的方法功能也可运行COMSOL自己开发的类JAVA语法命令流实现参数化建模，同时COMSOL提供了与MATLAB的LiveLink接口[18]，可实现数据及命令流的实时交互。因此本文基于MATLAB，读取DEM计算得到的稳定堆积状态下硅酸锂颗粒的位置坐标，并通过LiveLink接口实现在COMSOL内颗粒几何结构的重构。模型重构流程如图4所示。

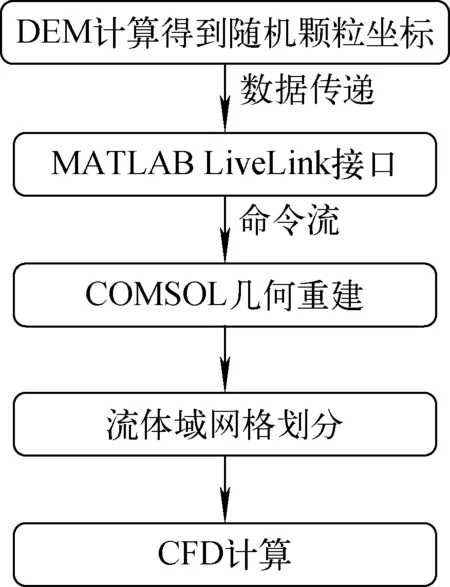
图4 COMSOL几何重建流程Fig.4 Pebble bed structure rebuilding procedure in COMSOL

重建的CFD计算模型如图5a所示，球床在轴向设置了相应的进出口段以减小气体流动的出入口效应。通过布尔运算抽取球床内的复杂流道进行网格划分，在网格划分时颗粒接触位置网格变形较大，因此需对模型内颗粒间接触进行处理。常用于球床颗粒间接触的处理方法有缩径法[19]、扩径法[20]、剖切法[21]、搭桥法[22]等。缩径法的思路是通过减小颗粒半径以避免颗粒间的点接触，扩径法、搭桥法的思路是将点接触扩大为面接触以降低网格划分难度。其中搭桥法最大程度地保留了球床颗粒间的接触信息，且用于搭桥的圆柱体半径一般小于颗粒半径的1/10，对球床的孔隙率分布影响极小，因此本文采用搭桥法处理颗粒间接触，处理后的颗粒间接触如图5b所示。

a——重建的COMSOL模型；b——搭桥法处理的颗粒接触图5 重建的COMSOL模型与处理后的颗粒接触Fig.5 Rebuild model in COMSOL and particle contact after treatment

2) 网格无关性验证

氦冷固体包层采用氦气作吹扫气体，运行压力为101 kPa。以流动场计算为例，计算模型采用速度入口、压力出口，内部颗粒壁面及圆柱容器壁面为无滑移边界，在吹扫气体流速范围(0.1～2.0 m/s)内Re均处于层流模型适用范围，因此计算模型采用层流稳态计算。模型采用四面体网格，分别划分了224万、292万、326万与401万4套网格进行网格无关性验证，入口流速0.1 m/s下的球床压降计算结果列于表2。由表2可知，当网格量大于326万后压降计算结果差别很小(相对误差小于1%)，因此本文采用网格量为326万的计算结果作为分析对象，其网格划分示意图如图6所示。

表2 网格无关性验证Table 2 Mesh independence verification

2 计算结果分析与讨论

2.1 球床结构下氚在吹扫气体内的等效扩散系数

氚在氦气中的自由扩散系数由Chapman-Enskog公式计算：

(2)

其中：k为玻尔兹曼常数；Tg为气体温度；M为等效摩尔质量；ni、nj分别为组分i、j的原子数密度；ε0为修正因子；Ωi,j为扩散碰撞积分因子，详细推导过程参见文献[23]。593 K下，氚在氦气中的扩散系数为1.78×10-4m2/s。

在球床结构下，复杂曲折的内部区域使气体分子平均输运路径增加，因此若使用多孔介质模型对氚增殖球床进行氚的输运行为模拟，需对氚在氦气中的扩散系数进行修正。具体计算流程如下：1) 建立带有入口段和出口段的球床随机堆积模型；2) 物理场采用稀物质传递场，在入口段和出口段设定浓度边界；3) 对稀物质传递场进行稳态计算；4) 由通量连续条件，得到球床段等效扩散系数。

稳态下氚浓度分布如图7所示，计算模型入口段、球床段、出口段通量连续，即：

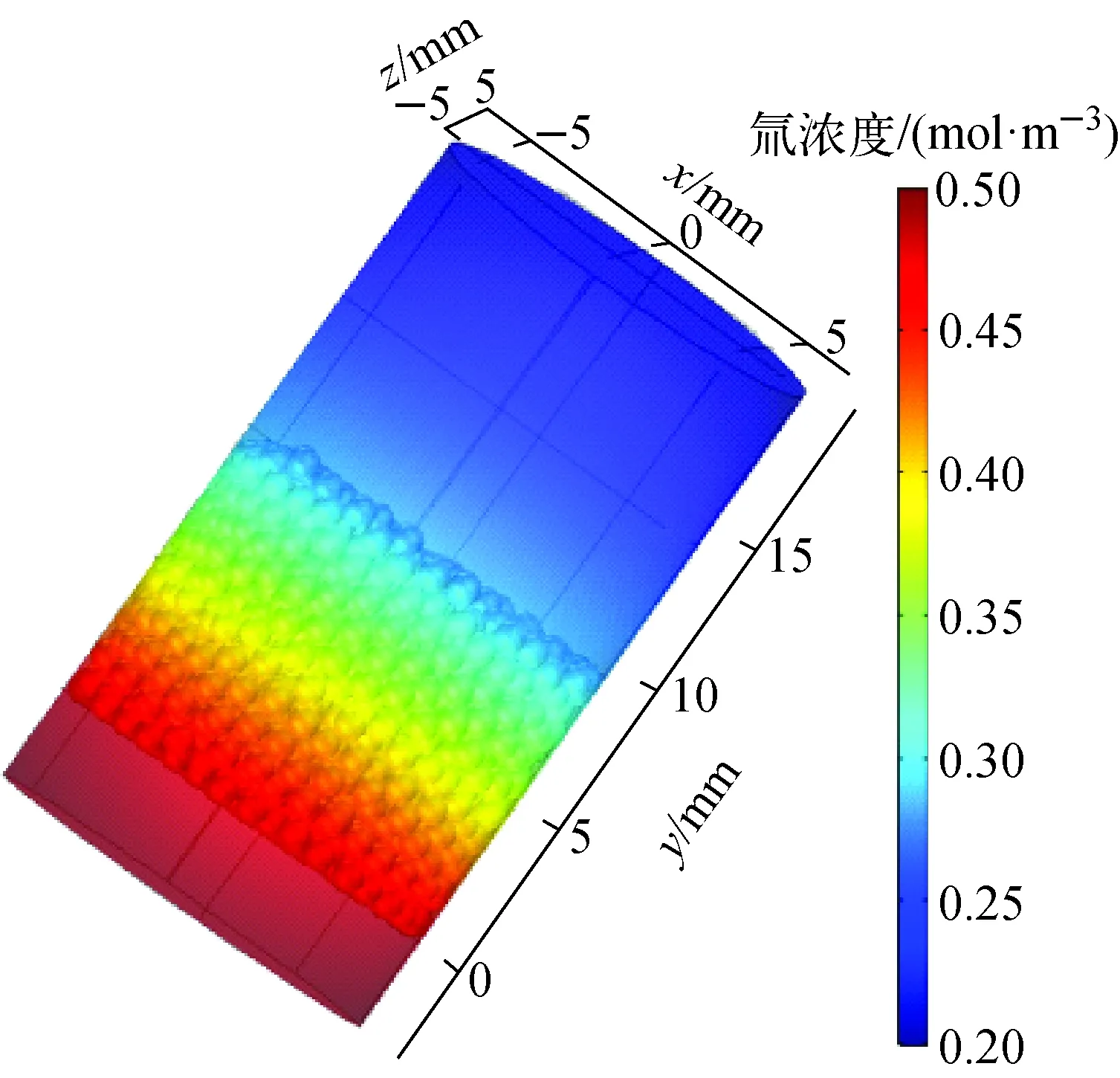
图7 稳态下氚浓度分布Fig.7 Concentration of tritium in pebble bed under steady state

J入口段=J球床段=J出口段

(3)

由Fick定律，可得球床段氚的等效扩散系数：

(4)

其中：D为氚在氦气中的扩散系数；Deff为球床结构下氚的等效扩散系数；ΔcT为各段氚浓度差值；Δx为各段长度。因此，若采用多孔介质模型对氚增殖球床进行氚输运模拟，球床结构影响下氚在吹扫气中的等效扩散系数Deff=0.4D。

2.2 吹扫气体流动压降分析

球床通道内流体的流动压降用Ergun方程描述：

(5)

其中：ε为球床孔隙率；μ为氦气动力黏度；dc为球床直径；ρ为氦气密度；C1与C2分别为黏性阻力与Forchheimer阻力系数。层流下，式(5)可简化为Blake-Kozeny压降方程：

(6)

不同入口流速下球床通道内流体的流动压降示于图8，拟合所得Blake-Kozeny方程系数C1=87。

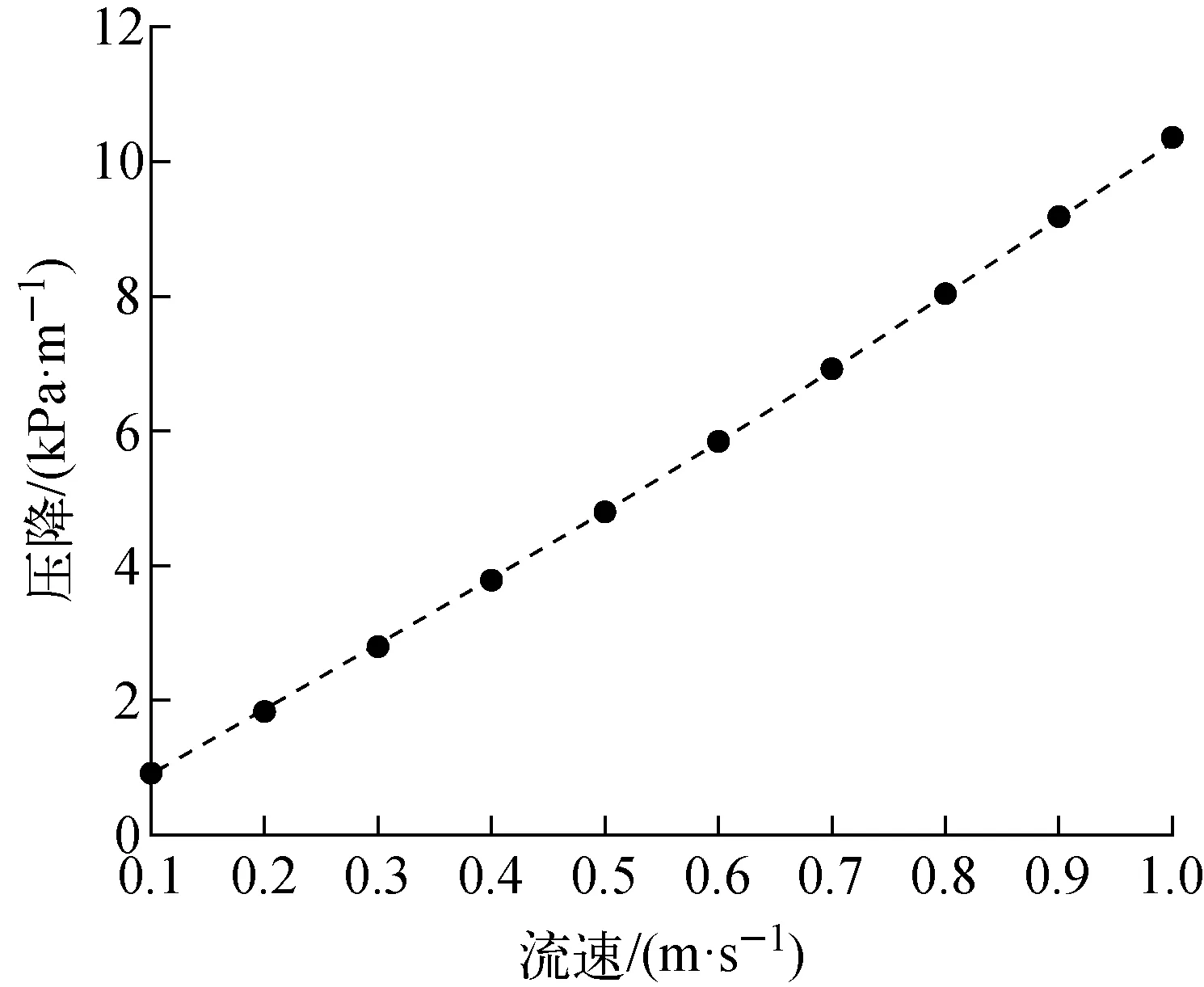
图8 不同入口流速下的流动压降Fig.8 Pressure drop under different inlet velocities

2.3 吹扫气体流动特性分析

吹扫气体轴向速度分布如图9所示。可看到，球床区域气体流速变化剧烈，吹扫气体不断经历加速、减速过程，在孔隙率较大的位置由于流动阻力较低，出现气体流动加速现象。在球床内部填充较紧实的区域颗粒背部气体流速缓慢，出现较多流动迟滞区(流速小于10-2m/s)，在近壁面区域由于球床壁面效应，孔隙率较大，流动阻力降低，气体流速较大。

图9 y=0截面速度云图Fig.9 Velocity distribution of axial central cross section

2.4 吹扫气体流动特性多孔介质模型验证

为对球床精细模型得到的流动阻力特性进行验证，采用自定义径向孔隙率的二维轴对称模型进行数值模拟，如图10a所示，模型尺寸与球床精细模型保持一致，采用结构化网格进行网格剖分，如图10b所示。流动压降与多孔介质模型计算结果示于图11，可见二者符合较好。径向流速分布如图12所示，呈现与孔隙率分布(图3)相反的波动现象，即在孔隙率较低处流动阻力减小，流动加速。

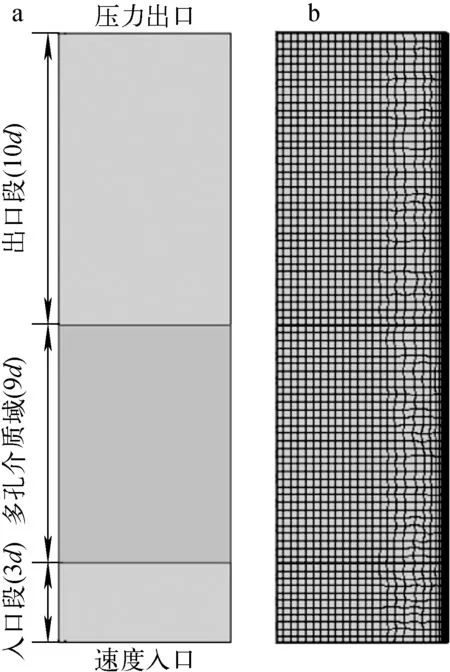
图10 二维轴对称多孔介质模型Fig.10 Two-dimensional axisymmetric porous media model

图11 压降计算结果对比Fig.11 Comparison of pressure drop calculation results

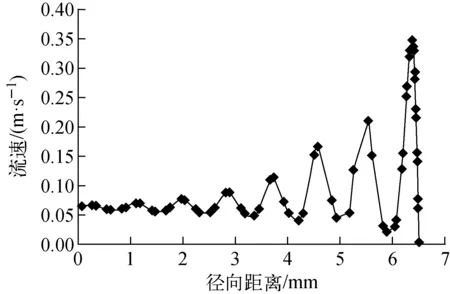
图12 径向流速分布Fig.12 Radial flow velocity distribution

2.5 球床等效导热系数模拟

骆贝贝等[11]针对硅酸锂球床开展了堆内辐照环境下的等效导热系数的测量实验，并与理论值和堆外实验结果进行了对比，结果表明辐照实验下硅酸锂球床的等效导热系数略低于理论值和堆外实验值。由于ZBS模型及堆外实验均基于外加热流的边界条件，因此本研究进行了外加热流与内热源两种工况下的模拟分析。由于提氚气体(氦气)流速较低，从保守角度假设氦气为静止状态，为减小模型计算量及降低壁面效应的影响，提取球床内部径向孔隙率变化较低的部分进行模拟计算。模型如图13所示，蓝色区域为硅酸锂颗粒，灰色区域为氦气，采用四面体网格进行网格划分，在颗粒-氦气及颗粒-颗粒接触处进行局部加密，总网格量达1 122万，网格划分如图14所示。

图13 球床导热模型Fig.13 Thermal conductivity model of pebble bed

图14 球床网格划分示意Fig.14 Schematic view of mesh

1) 外加热流工况

该工况下模型顶部为加热面，热流密度为1 000 W/m2，模型底部为定温壁面，其余边界为绝热边界。改变模型底部温度，分别计算底部温度为473、573、673、773、873 K时球床平均温度对应的等效导热系数。由于热流连续，等效导热系数可直接由傅里叶定律计算：

keff=q″/(∂T/∂z)

(7)

其中：keff为球床等效导热系数，W/(m·K)；q″为模型z方向热流密度，W/m2；∂T/∂z为z方向温度梯度，K/m。对5种平均温度对应的等效导热系数进行线性拟合，得到:

keff=0.951+2.778×10-4T

(8)

其中，T为球床平均温度，K。

2) 内热源工况

设定该工况下硅酸锂颗粒为体热源，功率密度为1 MW/m3，模型圆周面为定温边界，上下表面为绝热边界。同样进行了定温边界温度为473、573、673、773、873 K时球床平均温度对应的等效导热系数计算。由于有内热源工况下球床内传热路径复杂，不满足热流连续条件，因此从导热控制方程出发进行等效导热系数推导。

对于硅酸锂颗粒、氦气，有：

(9)

其中：ks、kf分别为硅酸锂颗粒与氦气的导热系数，W/(m·K)；qv为硅酸锂颗粒的功率密度，W/m3。

将球床等效为均匀多孔介质，则球床整体满足有内热源下的圆柱导热方程：

(10)

(11)

其中，tw为定温边界温度。对模型不同半径处温度取平均值，可得到平均温度下的等效导热系数，经线性拟合，有：

keff=0.834+2.818×10-4T

(12)

3) 球床等效导热系数分析

Liu等[10]对采用稳态热流法对堆积率为59.7%的硅酸锂球床的等效导热系数进行了实验测量，线性拟合曲线为：

keff=0.753+5.17×10-4T

(13)

骆贝贝等[11]基于CARR堆内辐照实验得到的球床导热系数与温度的关系为：

keff=0.647+4.074×10-4T

(14)

外加热流工况、内热源工况、CARR堆内辐照实验、Liu等[10]的稳态热流实验得到的球床等效导热系数对比示于图15。由图15可看出，内热源工况下的球床等效导热系数均略低于外加热流工况下的等效导热系数，CARR堆内辐照实验的球床等效导热系数最低，可能是由于CARR实验中硅酸锂球床堆积率较低(56%)，导致球床接触热阻相对较大；而本研究中两种工况采用相同的球床结构，有内热源工况下的球床等效导热系数仍低于外加热流工况。刘子平等[24]对高温气冷堆采用的包覆型颗粒燃料的等效导热系数进行了理论推导，同样得到在有内热源情况下燃料球等效导热系数低于无内热源情况下等效导热系数。相较于外加热流工况，在有内热源工况下，球床内传热工况更加复杂，外加热流下的热阻简单并联模型并不适用，内热源的存在降低了热流方向上的温度差，即增加了热流方向上的热阻，导致球床整体等效导热系数降低。有内热源工况更符合硅酸锂球床实际运行状态，从保守分析角度，建议球床导热系数采用有内热源工况下的球床等效导热系数。

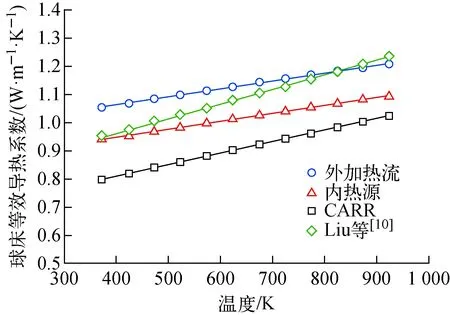
图15 硅酸锂球床等效导热系数模拟值与实验值对比Fig.15 Comparison of simulated and experimental results of Li4SiO4 pebble bed

3 结论

通过离散单元法生成了硅酸锂颗粒随机堆积模型，并对球床结构下氚在吹扫气体内的等效扩散系数及吹扫气体流动及球床导热进行了CFD计算。计算结果表明：球床复杂曲折的内部结构使气体分子平均输运路径增加，氚在吹扫气体内的等效扩散系数Deff=0.4D；吹扫气体在球床内的流动压降可由Blake-Kozeny方程预测，经拟合得到Blake-Kozeny方程系数C1=87；内热源的存在降低了热流方向上的温度差，导致球床整体等效导热系数低于外加热流工况下的球床等效导热系数。

本文通过对硅酸锂球床开展DEM-CFD耦合计算，获得了氚在吹扫气体内的等效扩散系数、吹扫气体流动压降及球床等效导热系数等宏观参数，可在此基础上基于多孔介质模型对固态包层进一步开展球床传热及氚输运行为模拟。此外，本文结果对包层氚提取系统设计也具有一定的参考价值。