永磁悬浮轨道侧向力控制系统的DMC−PID控制策略

2021-08-02过振宇杨杰

铁道科学与工程学报 2021年6期

过振宇，杨杰

(江西理工大学电气学院，江西赣州341000)

目前，世界上磁悬浮列车常用的悬浮方式是电磁悬浮[1]EMS以及超导磁浮[2]EDS，但至今磁悬浮列车无法大面积推广，其很大原因是无论是电磁悬浮还是超导悬浮，都无法解决断电情况下的列车安全性问题。电磁悬浮是利用车载悬浮电磁铁与车轨磁体的吸引力进行悬浮，需电能供应。而超导磁浮是通过运动的车载超导磁体(通有电流的线圈)的磁场与车轨两侧铝环线圈相切，铝环线圈感应出磁场，超导磁体本身的磁场与感应的磁场产生斥力进行悬浮的。超导磁浮的悬浮高度与悬浮列车运行速度有关，且停车时需利用单独辅助支持轮支撑，因此，超导磁浮悬浮高度不稳定并且也需要提供电能。与电磁悬浮以及超导磁浮的悬浮方式不同，永磁悬浮[3]轨道交通系统(又称“虹轨”)是完全利用车载稀土永磁体与磁轨稀土永磁体之间的纯磁性斥力进行悬浮，悬浮过程无需提供电能，能实现“零功率”悬浮，悬浮高度只与永磁体本身和永磁体之间间隙有关，与悬浮列车运行速度以及电能无关，无需装设辅助支持轮装置，不存在断电情况下列车悬浮的安全性问题。它是一种新型悬挂式轨道交通模式，具有无功耗、结构简单、体积小、成本低等优点，由江西理工大学于2014年首次提出，2019年初完成安装、调试、系列实验。由于“虹轨”独特的悬浮方式，其存在包含自身特点的列车转弯时永磁体偏移产生侧向力问题。当悬浮列车在转弯时，由于离心力的作用，悬浮列车将向外偏移，导致车载磁体与轨道磁体不对中，进而产生侧向力，侧向力的方向与离心方向一致，如果不加以控制，侧向力将随着偏移量增加而不断增大，导致悬浮列车一直处于侧偏状态，对列车导向轮损坏较大，影响车辆安全，而如果控制效果不好，将使得永磁悬浮列车左右摇晃剧烈，平稳性变差。针对以上永磁悬浮系统在转弯处存在侧向力较大的问题，本文提出在悬浮架导向轮上增加液压控制系统，通过控制两边导向轮上数字液压缸的伸缩使得车载磁体与轨道磁体对中，侧向力趋近于0，并提出了一种DMC-PID串级控制的针对永磁悬浮轨道侧向力控制系统的控制策略，将传统PID和动态矩阵算法的优势结合在一起[4]，可以解决永磁悬浮轨道侧向力系统大惯性、纯滞后以及非自衡问题。本文首先阐述永磁悬浮轨道弯道侧向力控制系统的弯道侧向力控制原理与策略以及建立被控对象模型，其次设计了基于DMC-PID串级永磁悬浮侧向力控制系统，最后通过数值仿真实验证明了DMC-PID策略在永磁悬浮侧向力控制系统上的优越性。

1 永磁悬浮轨道弯道侧向力控制系统

1.1 弯道侧向力控制原理与策略

控制原理：永磁悬浮列车弯道运行状态示意图如图1所示。当悬浮列车经过弯道时，由于离心作用悬浮架会向远离圆心方向偏移，将产生悬浮侧向力。悬浮列车向心力F向心由天梁给悬浮架的支持力F支与悬浮架发生偏移后悬浮侧向力F侧向的合力提供：

图1 弯道运行状态示意图Fig.1 Schematic diagram of curve running state

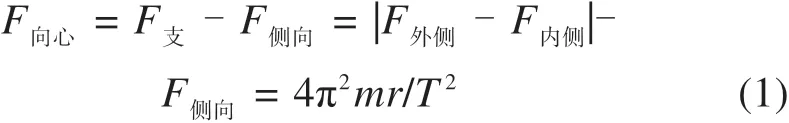
式中：m为悬浮列车质量；r为弯道半径；T为悬浮列车运行周期(匀速运动)。由于m，r，T都是已知量，因此F向心趋近于常数。

控制策略：永磁体对中具体控制策略框图如图2所示，给定的F向心与压力传感器反馈的两侧轮液压缸压力差值(指天梁给悬浮架的支持力)F支的偏差e作为控制器的输入，经过控制算法得出合适的输出脉冲数u，进而驱动数字液压缸伸缩动作来控制两侧悬浮架导向轮的伸缩，实时调整车载磁体和磁轨之间的横向位移状态，最终实现车载磁体和磁轨磁体两者位置对中，此时悬浮侧向力趋近于0。

图2 永磁体对中具体控制策略框图Fig.2 Block diagram of specific control strategy for permanent magnet alignment

1.2 被控对象模型建立与辨识

永磁悬浮轨道侧向力系统被控对象由数字液压缸和永磁悬浮模块2部分组成，分别对2部分被控对象的模型进行建立与辨识。

1.2.1 数字液压缸对象模型建立

为解决永磁悬浮列车转弯过程中车载磁体与轨道磁体不对中侧向力偏大问题，永磁悬浮侧向力控制系统采用数字液压缸作为执行机构来控制悬浮架导向轮的伸缩。该数字液压缸主要由4部分构成：步进驱动电机、四边滑阀、液压缸体以及信号反馈机构。数字液压缸数学模型表达形式[5−7]：

式中：kq为阀的流量增益；Ap为液压缸活塞有效面积；wh为液压固有频率；ξh为液压阻尼比；kf为齿条和齿轮的传动比。

已知一数字液压缸的基本参数如下。

阀的流量增益：kq=0.012；

液压缸活塞有效面积：Ap=0.01 m2；

液压固有频率：wh=9；

液压阻尼比：ξh=0.3；

齿条和齿轮的传动比：kf=2π；

该数字液压缸的闭环传递函数为：

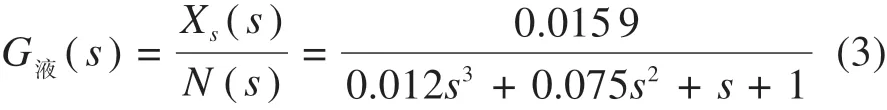
式中：Xs为液压缸活塞伸缩量；N为步进电机的输入脉冲数。

1.2.2 悬浮模块系统模型辨识

悬浮架在转弯过程中整体发生侧偏，车载磁体与磁轨磁体不对中，示意图如图3所示，其中，磁体内部箭头方向—磁体磁化方向，X轴为悬浮列车横向偏移方向，Z轴为悬浮列车上下浮动方向。

图3 车载磁体与磁轨磁体不对中示意图Fig.3 Schematic diagram of misalignment of vehicle magnet and magnetic track magnet

纵向长度皆为L的车载磁体与磁轨磁体在X轴方向偏移c时所产生的侧向力F侧向的计算方法[8]如下：

式(4)~(10)中，a为磁轨磁体宽度；b为磁轨磁体高度；c为磁轨与车载磁体偏移量；d为车载磁体高度；e为车载磁体宽度；h为永磁悬浮高度；L为车载以及磁轨磁体长度；u0=4π×10-7H/m为空气磁导率；Br1为车载永磁体剩磁感应强度；Br2为磁轨永磁体剩磁感应强度。

为了增强工作气隙的磁场及磁能，本永磁悬浮轨道系统的悬浮模块采用Halbach永磁阵列排布方式。车载永磁体与轨道永磁体都采用钕铁硼(N45)材料。其性能及其尺寸参数如下：

将以上相关参数代入式(4)～(10)，采用Matlab绘制列车侧向力随车载与磁轨磁体偏移量变化的趋势图，并利用Matlab专用辨识工具对此永磁悬浮模块系统模型进行传递函数辨识，该永磁悬浮模块辨识对比结果如图4所示，X轴为磁轨与车载磁体偏移量c，在实际应用情况下，磁轨与车载磁体的最大偏移量在35 mm左右，因此该辨识系统偏移量c取[0,35]，单位mm；Y轴为侧向力F侧向，单位N。

图4 永磁悬浮模块系统辨识结果Fig.4 Identification result of permanent magnetic levitation module system

由图4可知，永磁悬浮列车侧向力F侧向与车载磁体与磁轨磁体的偏移量c成正比，随着偏移量增大，永磁悬浮列车侧向力一直增大[9−10]，最终无法趋近于某个常数。因此，整个永磁悬浮侧向力控制系统属于非渐进稳定系统(非自衡系统)。永磁悬浮模块系统辨识精度为98.74%。由此可知，永磁悬浮模块系统传递函数为：

式中：F为车载磁体与磁轨磁体侧偏产生的侧向力；Xp为车载磁体与磁轨磁体偏移量。

1.2.3 控制对象传递函数模型建立

永磁悬浮轨道侧向力控制系统传递函数方框图如图5所示。

图5 控制对象传递函数方框图Fig.5 Block diagram of control object transfer function

当前时刻KT的车载磁体与磁轨磁体偏移量Xp(k)与当前时刻KT的液压缸活塞伸缩量Xs(k)以及上个时刻(K-1)T的车载磁体与磁轨磁体偏移量Xp(k-1)的关系：

将式(12)转换成Z域，再转换成S域：

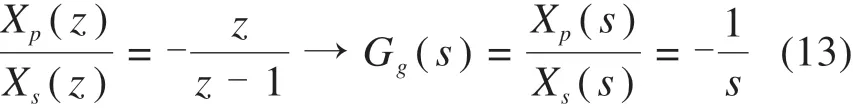
永磁悬浮轨道侧向力系统被控对象传递函数：

2 基于DMC-PID串级永磁悬浮侧向力控制系统设计

2.1 系统框图设计

本系统控制部分由内环PID和外环DMC双控制器组成。由于永磁悬浮侧向力控制系统不是一个渐进稳定的系统，因此先选择PID控制器使得系统渐进稳定，将PID控制系统当成一个广义对象，再采用先进DMC控制算法进行控制，形成了基于永磁悬浮侧向力控制系统DMC-PID串级控制策略。本系统框图如图6所示。

图6 永磁悬浮轨道侧向力控制系统方框图Fig.6 Block diagram of lateral force control system for permanent magnetic levitation track

DMC控制策略与PID策略不同，它不仅与目前和过去偏差值有关，还与预测模型预测出来的未来偏差值有关联，利用滚动优化给出目前最优控制策略[11]，使得未来一段时间实际侧向力值与目标侧向力值偏差最小。

2.2 控制器设计

2.2.1 PID控制器设计

永磁悬浮侧向力系统采用临界比例度法对PID参数进行整定，详细整定步骤如下：

首先，将积分系数Ki和Kd微分系数置0，比例系数Kp选取偏大一些的值。

其次，不断减小Kp值，直到曲线出现等幅振荡，记录当时的比例系数Ku和等幅振荡周期Tu。

最后，通过参考表1的临界比例度法整定公式，计算得到Kp，Ti和Td的值。

表1 临界比例度法参数整定公式Table 1 Parameter tuning formula of critical proportionality method

最终通过不断调整，得出最终PID整定参数：

2.2.2 DMC控制器设计

DMC控制器由预测模型、滚动优化和在线校正3部分构成[12−14]。

1)预测模型采用系统阶跃响应输入输出数据建立预测模型[15]。基于PID控制的永磁悬浮侧向力控制系统的单位阶跃响应曲线，如图7所示。当在k时刻对对象施加一个控制增量Δu(k)时，仅Δu(k)起作用的情况下能得到未来时刻对象的N个输出值。假设对象基于阶跃响应下的模型预测向量为a=[a1,a2,…,aN]T，则对象未来时刻的P个预测输出值向量可表示为：

图7 基于PID控制的永磁悬浮侧向力控制系统的单位阶跃响应曲线Fig.7 Unit step response curve of a permanent magnet levitation lateral force control system based on PID control

式(15)～(18)中：y0(k)为模型输出初始值；ym(k)为k时刻在控制增量Δu(k)作用下的模型预测值；P为预测时域长度；M为控制时域长度；N为模型时域长度；(k+1,k)为在k时刻对k+1时刻的预测。

DMC参数的选择：

a)采样周期T：取值需满足香农采样定理，对于滞后系统，在0.25Ti左右，不能取值太大，Ti=2.9—纯滞后时间；

b)模型长度N：取值尽可能使得模型预测向量a=[a1,a2,…,aN]T包含整个动态响应信息。T取值越大，N取值越小，系统抗干扰能力变弱；

c)优化时域P：P取值越大，系统稳定性好但响应速度慢；P取值越小，系统动态响应快，但稳定性差。

d)控制时域M：M取值越小，系统稳定性好但响应速度慢；M取值越大，系统动态响应快，但稳定性差。

根据上述DMC参数选定方法不断仿真实验调整得出最优的DMC参数：采样周期T=1，N=350，P=100，M=1。

2)滚动优化滚动优化[16]的目的是使系统未来p个时刻的预测输出值y͂(k+p)尽可能接近期望值ω(k+p)，需要确定M个控制增量Δu(k+m-1)，且控制增量的变化需受约束。而k时刻优化性能指标：

式中：qi和rj为加权系数，用来约束预测偏差和控制增量的改变。

qi参数优化整定方法：

a)先设定qi=0(i=1,…,P)，再选择合适的P值，尽可能包含系统主要动态特性；

b)观察系统动态曲线，如果动态响应太慢，则适当减少P值；如果稳定性差，则适当增大P值；

c)若系统静态误差偏大，则适当增大qi值。

rj参数优化整定方法：

a)先置rj=0(j=1,…,M)，如果系统动态稳定但控制量变化幅度太大，则可适当增加rj值；

b)在仿真过程中，rj取值很小就可以让控制量变化趋于稳定。

最终调整得最优加权系数：qi=0(i=1,…,P)；rj=0.1(j=1,…,M)。

3)在线校正

在线校正目的是实时校正未来时刻预测值。实时校正是在下一时刻将对象的实际输出y(k)与式(15)得出的未来时刻预测值y m(k)进行差值运算：

采用增加校正向量h的方式不断修正未来时刻预测值：

式中：h=[h1,h2,…,h350]T—校正向量，本系统中h1=h2=…=h350=0.9；yp(k+1)—修正后的输出预测值，通过s矩阵柔化后又重新成为下一个时刻的输出预测初始值，可表示为向量形式：

式中：s为柔化系数矩阵[17]，

3 仿真与结果分析

根据DMC-PID串级控制原理采用MATLAB SIMULINK工具建立控制系统仿真框图，如图8～9所示。DMC控制器的预测模型、在线校正以及滚动优化模块均使用MATLAB Function方式来自定义函数。建立永磁悬浮轨道侧向力控制系统仿真框图是为了对比传统PID控制策略与DMC-PID串级控制策略的控制效果。

图8 2种控制方案仿真Fig.8 Simulation diagram of two control schemes

图9 永磁悬浮侧向力控制系统内部封装Fig.9 Internal package diagram of permanent magnetic levitation lateral force control system

仿真结果如图10和图11所示，横坐标为时间(s)，纵坐标为侧向力(N)，其中，系统侧向力初始值是1 000 N(相当于车载磁体与磁轨磁体初始偏移量约15 mm)，目标值设定为0 N，侧向力为负值表示侧向力是相反方向的。

图10 未加扰动信号的仿真对比Fig.10 Simulation comparison chart of undisturbed signal

图10 是系统未加入扰动时2种控制方案的对应效果曲线图。由图10可知：当选用PID控制策略时，系统超调量约为58%，调节时间约为370 s。而选用DMC-PID串级控制策略时，系统超调量约为28%，调节时间约为210 s。因此，与传统PID控制策略对比，采用DMC-PID串级控制策略系统侧向力波动能够更快更稳得趋近于目标值0 N。

图11 是当系统受到外界扰动时(在600 s时刻加入车载磁体与磁轨磁体偏移量5 mm的扰动信号，相当于侧向力400 N)2种控制方案的对应效果曲线图。由图11可知：在抗干扰能力方面，DMC-PID控制策略明显优于PID控制策略。系统采用DMCPID控制策略侧向力曲线波动更小，调节时间更短，系统能够更快趋近于目标值0 N，系统抗扰动能力更强。