多元退化系统维修与备件订购策略优化模型
2021-08-02杨志远赵建民程中华郭驰名李俐莹
杨志远, 赵建民, 程中华, 郭驰名, 李俐莹
(1. 陆军工程大学石家庄校区 装备指挥与管理系,石家庄 050003;2. 河北科技大学 信息科学与工程学院, 石家庄 050000)
现代复杂系统通常装备有状态监测单元如传感器、仪表、计算设备[1],这为基于状态的维修(CBM)实施提供了系统状态数据.相对于基于时间的维修方式,CBM能够有效控制“维修不足”和“维修过度”的问题[2].通常来说,获取系统状态信息的方式可分为定期检测和连续监测两类,相比于定期检测,连续监测能够实时获取系统状态信息,从而更为及时有效地进行CBM决策,降低系统故障风险和维修费用.随着传感器技术的发展,连续监测的应用场景越来越多,特别是对于一些关键部件或系统,如发电机组,其本身价值高、停机损失大,对系统状态进行连续监测更为适用.同时,复杂系统通常存在多个退化过程,且由于共同的运行环境、应力等因素,退化过程间往往是相关的,在CBM决策中需要充分考虑这些因素[3],这也增加了多元退化系统CBM决策的难度.
对于有多个相关退化过程的系统而言,CBM决策的基础是对不同退化过程间的相关性进行建模描述.目前,常用的方法包括多维退化模型[4-5]、退化率相关模型[6-7]和基于Copula函数的退化相关模型[8-9].文献[4-5]分别采用多元正态分布和二元Birnbaum-Saunders(B-S)分布来描述不同退化过程间的相关关系,而分布形式也限制了此类方法的应用.文献[6-7]将不同退化过程间的相关关系表示为一个部件退化水平对其余部件退化速率的影响.在工程实际中,这种影响关系及程度很难采用定量化方法描述和确定.相对而言,Copula函数在定量描述随机变量相关性方面具有很高的灵活性,并且提供了分析相关结构对系统可靠性影响的参数化方法.基于不同种类的Copula相关结构,文献[10]利用仿真方法对定期检测策略下的系统维修费用进行分析,其中预防性维修阈值为固定值.文献[11]建立了多部件系统检测维修策略优化模型,其中部件故障间的相关性采用Gaussian Copula函数来描述.文献[12]采用Levy Copula函数描述系统二元退化间的相关关系,并在此基础上提出系统定期检测与机会维修策略,利用仿真方法获得了最优预防性维修阈值和机会维修概率阈值.在现有的基于Copula函数建立多元退化模型的文献中,很少研究在连续监测条件下的CBM决策优化问题,且没有考虑系统备件约束,而对一些价值较高的重要系统而言,很难保证时刻有可用备件,通常需要提前预定.在连续监测条件下,文献[13]研究了单一退化过程的预防性更换阈值优化问题.在此基础上,文献[14]考虑二元相关Levy退化过程,以系统长期运行条件下的期望维修费用率和可用度为准则,计算获得在不同系统结构下的最优预防性更换阈值.上述研究均是在维修延迟(维修资源的到达需要一定时间,此处的维修资源也可指备件)条件下,对预防性更换阈值进行决策,没有综合考虑备件订购阈值以及预防性维修阈值的优化问题.
针对上述问题,本文考虑系统不同退化过程间具有的相关性,利用Copula函数建立系统多元退化模型.在此基础上,提出系统维修及备件订购策略,分析直接维修费用、备件库存费用和故障停机损失,建立系统维修费用模型.以系统期望维修费用率准则,引入人工蜂群(ABC)算法搜索最优维修及备件订购策略,从而提高维修工作的经济性,为科学制定系统维修及备件订购计划提供方法支撑.
1 系统描述
系统性能会随着工作时间的增加不断退化,当退化超过阈值时会导致系统出现故障.假设系统存在n个相关性能退化过程,任意退化过程超过特定阈值时系统即会出现故障.
现有的退化过程模型主要包括退化轨迹模型、退化量分布模型和基于随机过程的退化模型等.相对于前两种模型,基于随机过程的退化模型能够描述性能退化在时间轴上的不确定性,更符合工程实际.在基于随机过程的退化模型中,Gamma过程由于其良好的性质,广泛应用于连续非减的退化过程建模,包括材料的磨损、侵蚀、裂纹、老化等.本文采用Gamma过程来建立系统退化过程模型.
令Xi(t),i=1,2,…,n表示系统第i个性能退化过程,根据Gamma过程平稳独立增量性质可知,对于任意t>u>0,Xi(t)-Xi(u)=Xi(t-u)~Γ(αi(t-u),βi),其中:Γ(·,·)为Gamma分布;αi>0和βi>0分别为形状参数和尺度参数.假设系统初始退化量均为0,那么Xi(t)的概率密度函数和概率密度分布函数可表示为
(1)
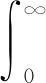
如上所述,本文采用Copula函数描述退化过程的相关性.为便于实际应用,这里假设:在不同时间间隔内,不同退化过程的退化过程增量间的相关性可忽略.在文献[8]中也采用了类似的假设分析多元Wiener退化过程的相关性.令t>u>0,根据Sklar定理,系统n个退化过程在时间区间[u,t]上退化增量Xi(t-u)的联合概率分布函数可表示为
Ht-u(x)=C(FX1(t-u)(x1),FX2(t-u)(x2),…,
FXn(t-u)(xn);θ)
(2)
其对应的概率密度函数可表示为
c(FX1(t-u)(x1),FX2(t-u)(x2),…,
(3)
c(FX1(t-u)(x1),FX2(t-u)(x2),…,FXn(t-u)(xn);θ)=
(4)
式中:C为Copula函数;c为Copula密度函数;x=[x1x2…xn],xi≥0;FXi(t-u)(xi)为第i个退化过程在[u,t]内增量的分布函数;θ=[θ1θ2…θm]为Copula函数中的参数向量,其取值直接影响着随机变量间相关关系强弱.对于Copula函数参数估计问题,可基于退化数据通过最大似然估计或边际推断(IFM)法分两步获得.在此基础上,可采用赤池信息准则(AIC)选择合适的Copula函数描述系统退化相关性.关于Copula函数的参数估计方法参考文献[15].
在此基础上,假设系统退化故障阈值向量为QL=[QL1QL2…QLn],可获得系统可靠度函数为
Rsys(t)=P(X1(t)≤QL1,X2(t)≤
QL2,…,Xn(t)≤QLn)=
Ht(QL)=C(FX1(t)(QL1),
FX2(t)(QL2),…,FXn(t)(QLn);θ)
(5)
式中:P为概率.
由于Gamma函数和不完全Gamma函数的影响,FXi(t)(QLi)的计算较为复杂,可采用B-S分布对其进行近似计算[16].FXi(t)(QLi)可近似表示为
FXi(t)(QLi)≈1-FBS(t;QLi)=
(6)
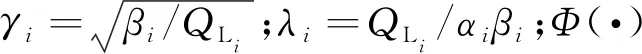
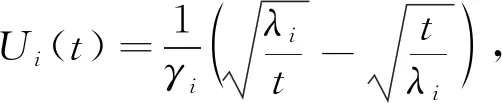
Rsys(t)=
C(FX1(t)(QL1),FX2(t)(QL2),…,FXn(t)(QLn);θ)≈
C(Φ(U1(t)),Φ(U2(t)),…,Φ(Un(t));θ)
(7)
2 系统维修与备件订购策略
本文的系统维修和备件订购采用控制限策略(CLP),即根据系统退化状态确定相应的备件订购和维修活动.备件订购阈值为QA=[QA1QA2…QAn],预防性更换阈值为QM=[QM1QM2…QMn].为建立系统维修与备件订购决策优化模型,对相关策略做出如下假设.
(1) 对系统在运行过程中的退化状态进行连续监测,系统各性能退化指标水平可以通过连续监测得到;单位时间状态监测费用记为CI.
(2) 初始备件库存为0,当系统任意退化过程达到备件订购阈值时,系统发出订货信号,备件经过时间τ后到达.此时,若系统不进行更换,会产生相应的备件库存费用;备件订购费用记为CO,单位时间库存费用记为CS.
(3) 当系统任意退化过程达到预防性更换阈值后,系统发出维修信号,如果此时库存中有备件,直接对系统进行更换;否则,在备件到达后对系统进行更换.更换后,系统修复如新,且之后系统退化过程与更换前的系统无关.如果备件是在系统故障后到达,即会产生停机损失,系统单位时间内的停机损失记为CLO.一般来说,系统维修更换费用与其退化量相关,退化量高的系统通常所需维修费用也较多.系统退化量是由多个退化过程共同决定的,由于各退化过程的故障阈值和量纲可能会不同,进而将影响系统退化量的计算.因此,首先定义各退化过程的相对退化量为
(8)
由式(8)可以看出,当任意χi(t)≥1时,系统处于故障状态.多退化过程引发的系统故障为竞争失效过程,系统状态由多退化过程中的最大相对退化量决定.基于此,系统在t时刻的维修更换费用可表示为
CMAN=CR+ρEsup(χt)
(9)
式中:Esup(χt)=max{E(χ1(t)),E(χ2(t)),…,E(χn(t))},E(χi(t))为χi(t)的期望;CR为系统更换固定费用;ρ为更换费用随系统退化量变化系数.
(4) 维修时间相对于系统寿命周期来说非常短,在建模过程中忽略不计.
(5) 为使备件订购阈值和系统预防性更换阈值有意义,令QAi≤QMi≤QLi,i=1,2,…,n.
以单退化过程为例,系统退化过程和更新过程如图1所示.其中:tA、tM和tL分别为退化过程到达备件订购阈值、预防性更换阈值及故障阈值的时间,且tL≥tM≥tA>0.
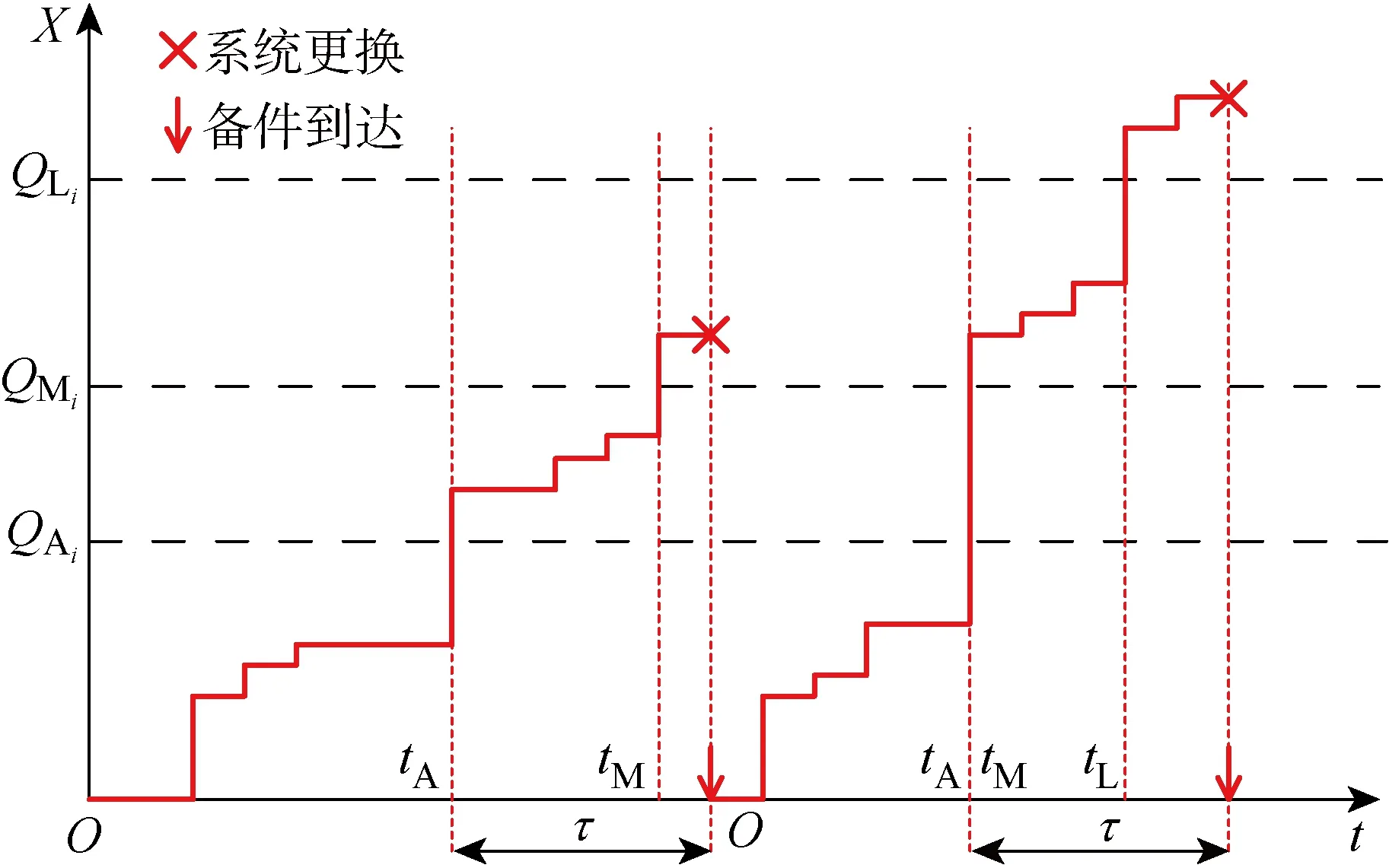
图1 系统退化和更新过程
对于Gamma过程而言,其退化路径为跳跃过程,因此有P(tM-tA=0)>0,P(tL-tA=0)>0,如图1中系统第2个更新周期内的退化过程所示.事实上,对于很多左极右连的Levy过程(包含Gamma过程)来说,均存在上述性质.
系统不同维修时机如图2所示.根据备件到达的时间不同,系统维修情况可划分为以下3种:

图2 系统的不同维修时机
(1) 当tA+τ (2) 当tM≤tA+τ (3) 当tA+τ≥tL时,在备件到达时对系统进行故障更换. 本文以系统长期运行情况下单位时间平均费用(即期望费用率)为指标,对系统预防性维修和备件订购策略进行评价.由前文分析可以看出,备件订购阈值和预防性更换阈值的高低会影响不同维修方式发生概率、维修费用、库存费用、更新周期长度,从而影响系统期望维修费用率. 考虑上述3种不同的系统维修情况,在不同情况下系统在一个更新周期内的维修费用C(T)及其相应的更新周期长度T可表示为 (1) 当tA+τ (10) (2) 当tM≤tA+τ (11) (3) 当tA+τ≥tL时, (12) 在此基础上,根据更新报酬原理可得系统的期望维修费用率为 γ∞=[CSE(max{tM-tA,τ})- CLOE(min{tL-tA,τ})+(CLO-CS)τ+ ρ(Esup(χtA+τ)-Esup(χtM))P(tM-tA≤τ)+ ρEsup(χtM)+CR+CO]/ [E(max{tM-tA,τ})+E(tA)]+CI (13) τGM(τ)+τ-τGM(τ)+ (14) (15) P(tM-tA≤τ)=1-P(tM-tA>τ)= (16) 由所建立的系统退化过程模型可得tA的生存函数为 P(tA>t)=P(X1(t) QA2,…,Xn(t) (17) 式中:Ht(QA)可由式(2)获得.在此基础上可得期望E(tA)的表达式为 (18) 在上述推导结果基础上,当τ为常数时,可得系统期望维修费用率表达式为 (19) (20) (21) 对于Esup(χtM)和Esup(χtA+τ),由定义可知: E(Xi(tM))=αiβiE(tM) (22) 式中:E(tM)与式(18)有类似表达式,此处不再赘述.在此基础上,可得: Esup(χtM)= (23) 同理可得: Esup(χtA+τ)= (24) 将式(21)、(23)和(24)代入式(19)即可得到系统期望维修费用率的解析表达式. 通过前文获得的系统期望维修费用率模型,可以得到相关的数值计算结果.但由于模型中涉及到x=[x1x2…xn]的高维积分,虽然在MATLAB等科学计算软件中集成了高维积分的数值算法,可以直接使用,但算法的计算复杂度较高.为简化计算,下面给出模型的近似表达式. 假设系统各退化过程在订货时间点tA的退化量已知,记为 XtA=[X1(tA)X2(tA) …Xn(tA)],那么容易得到: P(Xs (25) 由于退化过程均为随机过程,所以在实际中XtA为随机变量.因此,这里用XtA的期望值E(XtA)=[E(X1(tA))E(X2(tA)) …E(Xn(tA))]代替XtA.由此可得: Hs(QM-E(XtA)) (26) 同理可得: (27) (28) 在上述费用模型基础上,为制定最优系统维修与备件订购策略,以系统长期运行期望维修费用率最小为优化目标,对预防性维修阈值和备件订购阈值进行优化.基于此,建立如下优化模型 (29) s.t.0 在上述决策模型中,可以看出目标函数TC∞具有非线性、不可微的特点,且模型决策变量较多,当系统存在n个退化过程时,模型有2n个决策变量,因此,难以得到模型的解析解. 为解决这一问题,采用ABC算法搜索系统最优维修与备件订购策略.ABC算法是一种基于蜂群搜索蜜源行为的群体智能优化算法,在智能优化算法中属于比较新的算法,该算法控制参数少、易于实现、全局收敛性能好,并且其优化性能优于其他一些传统智能优化算法[17],如遗传算法(GA)、粒子群优化(PSO)算法、差分进化(DE)算法等,特别是在非线性优化函数求解方面具有良好的性能.ABC算法已广泛应用于解决各类优化问题,关于ABC算法的具体机理和优化过程可参考文献[18],这里不再赘述.在案例分析中,ABC算法采用MATLAB实现. 为验证上述决策优化模型的有效性,以两部件系统为例,即n=2,对系统维修及备件订购策略进行优化,并分析相关参数对模型优化结果的影响.考虑两种不同的情形,在案例1中假设系统两个退化过程参数相同,单位时间退化量均值为2,方差为4,故障阈值也相同;在案例2中假设系统两个退化过程参数存在差异,单位时间内退化量均值分别为2和1.5,方差分别为4和1,相应的故障阈值也不同.不同案例的退化过程及故障阈值参数如表1所示. 表1 系统退化过程及故障阈值参数 对于模型中的费用参数,为方便说明,假定单位时间系统状态监测费用为1,其余各项费用值均为与状态监测费用的比值.系统维修费用参数值如表2所示. 表2 系统维修费用参数 在Copula函数选择方面,以Gaussian Copula函数为例,描述系统两个退化过程间的相关关系,二元Gaussian Copula函数的分布函数为 (30) 式中:Φ-1(·)为标准正态分布逆函数.当表示两个变量间为正相关关系时,θ∈[0,1],在本案例中令θ=0.7.当然,这里也可以采用其他类型的Copula函数描述退化间相关关系,其分析过程相同. 在以上参数设置基础上,假设备件订购交付时间为τ=1.为验证期望维修费用率式(13)的准确性,在不同的维修及备件订购策略下采用Monte-Carlo(MC)方法对维修费用进行仿真,具体过程为:首先对系统退化过程进行仿真,得到备件订购时间、系统更换、系统故障时间,进而计算系统库存费用、更换费用及停机损失,最后得到费用具体值.在这里重复上述过程104次,得到系统维修费用的104个实现值.在此基础上,求得平均值并与解析结果进行比较,如表3所示. 表3 解析结果与仿真结果对比 由表3可以看出,解析方法得到的期望费用率与仿真结果很接近,并且在MC仿真结果95%置信区间内,由此说明了上述系统期望维修费用率表达式的准确性. 下面分析当备件订购阈值(QA1,QA2)为常数时,系统期望维修费用率γ∞随预防性更换阈值(QM1,QM2)的变化情况,结果如图3所示. 图3 γ∞随(QM1,QM2)变化情况 由图3可以看出,无论对于案例1还是案例2,当(QA1,QA2)为常数时,随着(QM1,QM2)的增大,γ∞总体上来说呈现先减小后增大的趋势,这是由库存费用、维修费用增加以及系统更新周期增长共同作用的结果.在给定的备件订购阈值下,存在最优的(QM1,QM2)使得γ∞达到最小.同理,下面固定预防性更换阈值(QM1,QM2),分析系统期望维修费用率γ∞随备件订购阈值(QA1,QA2)的变化情况,结果如图4所示. 由图4可以看出,无论对于案例1还是案例2,当(QM1,QM2)为常数时,随着(QA1,QA2)的增大,γ∞总体上来说呈现先减小后增大的趋势,这主要是受预防性更换概率减小、故障更换概率增大以及库存费用减少的影响.同样,在给定的预防性更换阈值下,存在最优的(QA1,QA2)使得γ∞达到最小. 图4 γ∞随(QA1,QA2)的变化情况 下面基于ABC算法对模型进行求解,得到最优维修及备件订购策略.在ABC算法中,设置种群数量为10,适应度函数为1/γ∞(QA,QM).以案例1为例,考虑到算法中随机因素的影响,运行ABC算法5次,获得的系统维修及备件订购策略优化过程如图5所示,其中:K为迭代次数;上标*表示最优. 图5 ABC算法优化过程 由图5可以看出,当迭代次数达到100次后,最优期望费用率值不再变化,且各优化过程均收敛于相同的最优值,对案例2也有类似的结果.当退化过程增多时,可适当增加算法中种群数量的设置,以提高算法收敛速度及精度.在此基础上,得到的系统最优维修及备件订购策略如表4所示.此外,假如在这里采取文献[14]中的策略,即不单独考虑系统备件订购阈值,而是在预防性更换阈值(QM1,QM2)处订购备件,即QAi=QMi.在此策略下,所获得的系统最优维修策略见表4. 表4 系统最优维修及备件订购策略 图6 不同(QA1,QA2)下和γ∞对比 图7 备件交付时间对优化结果的影响 下面分析θ的变化对系统最优维修及备件订购策略的影响,在案例1和案例2规定的情形下,计算结果如表5所示. 表5 不同θ下的系统最优维修及备件订购策略 多元退化系统CBM决策通常需要考虑不同退化过程间的相关性.在维修策略中同时考虑预防性更换阈值和备件订购阈值,在推导系统退化状态到达各阈值时间联合分布基础上,得到了连续监测条件下的系统期望维修费用率精确和近似表达式.在案例分析中,通过ABC算法得到了最优维修和备件订购策略,验证了模型和算法的有效性.通过和已有策略的对比表明了所提系统维修和备件订购策略的优势.同时,在案例中也检验了系统期望维修费用近似表达式的精度,分析了备件交付时间和退化相关程度参数对决策结果的影响.值得注意的是,本文采用Gamma过程建立退化过程模型,事实上,对于包含Gamma过程的Levy过程来说,上述模型也同样适用.此外,对于一些非Copula相关的多元退化系统在连续监测下的维修阈值优化问题,可参考上述方法建立优化模型.3 费用模型
3.1 期望维修费用率计算
3.2 具体表达式推导
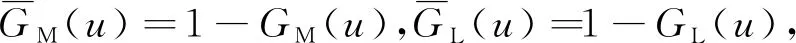
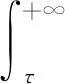

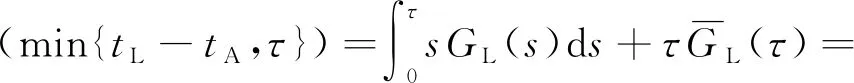

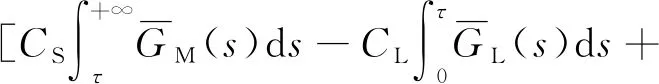

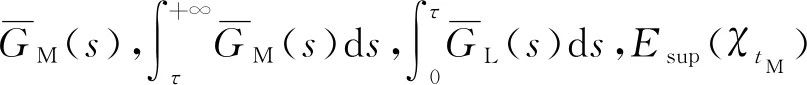
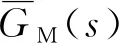
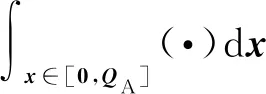
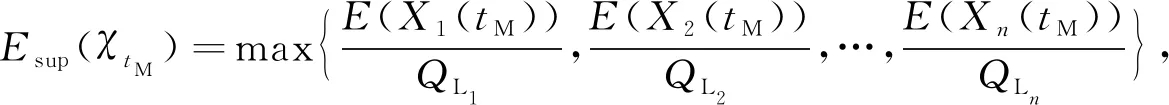
3.3 期望维修费用率估算
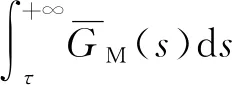
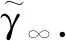
4 优化模型及算法
5 案例分析
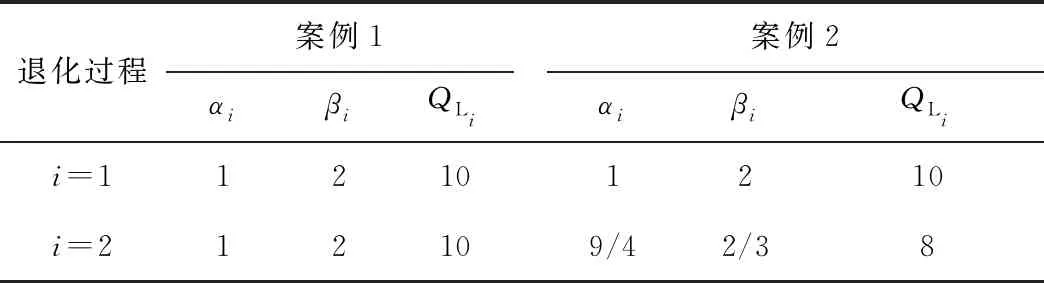
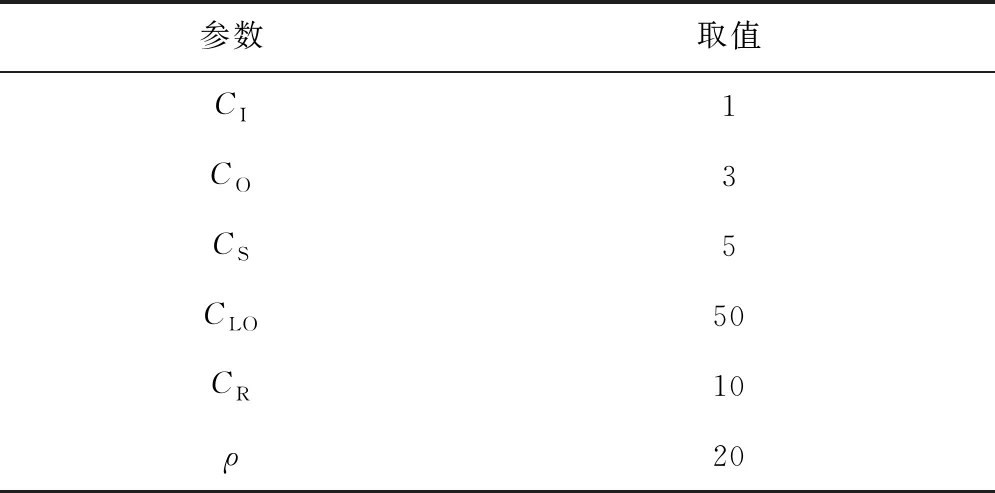
5.1 系统维修及备件订购策略优化
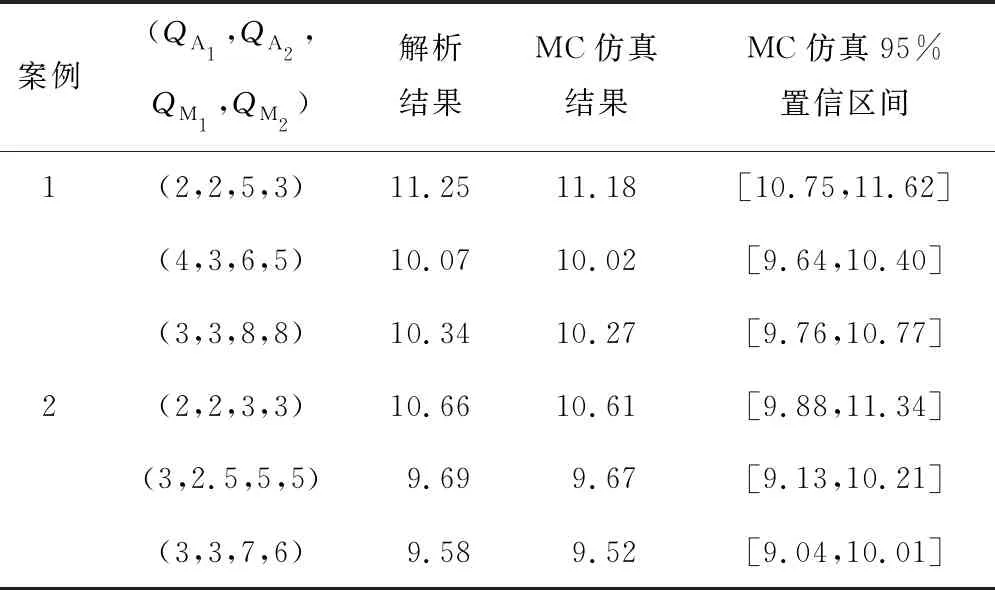

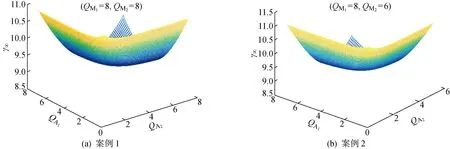
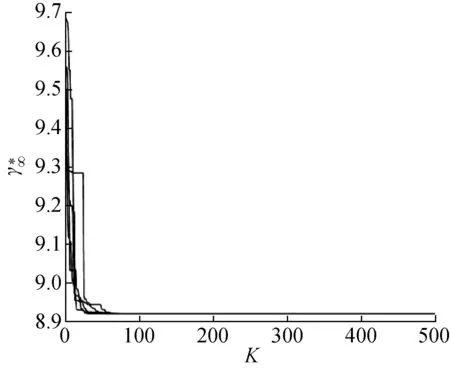

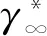
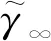
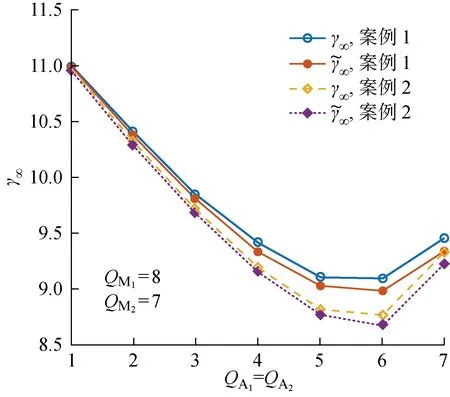
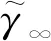
5.2 灵敏度分析
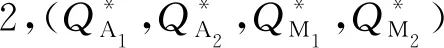
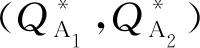
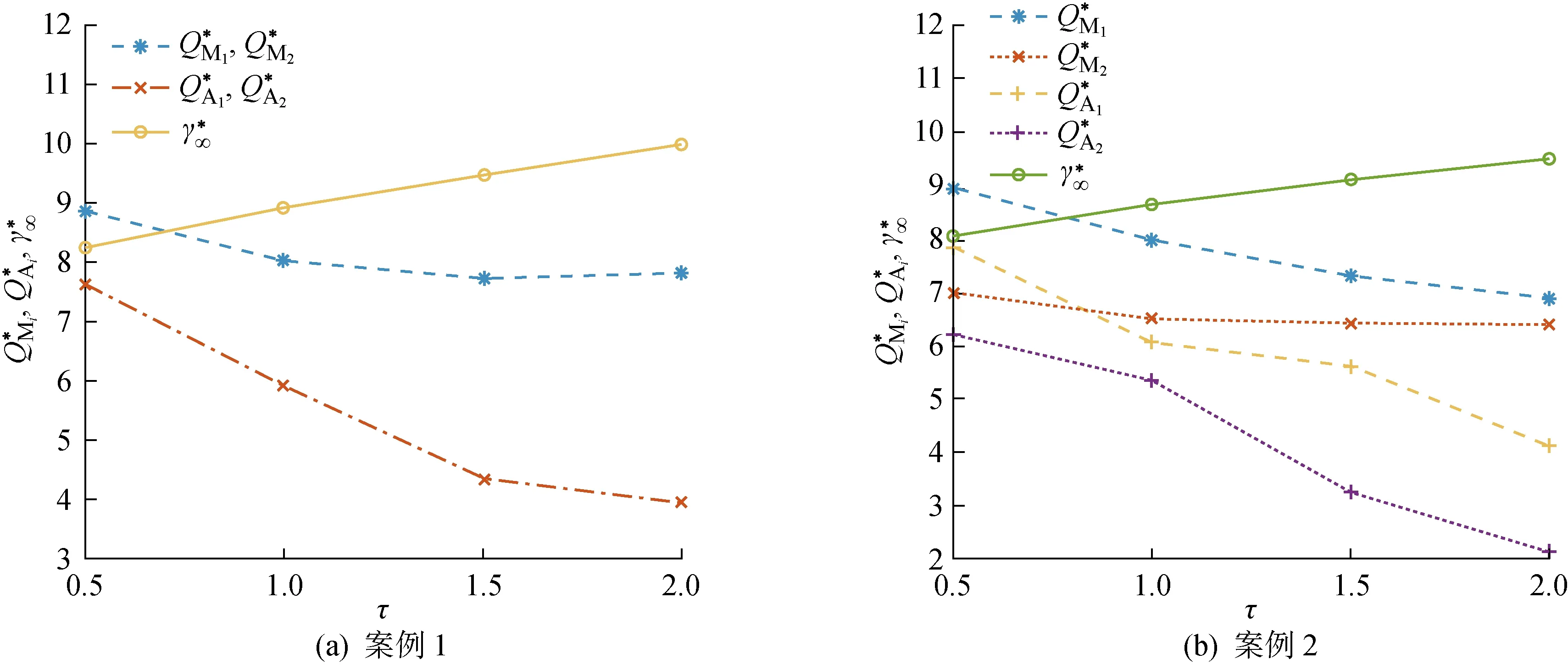
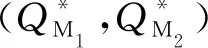

6 结语
