可变环境温度下锂离子电池平均温度估计

姜 余， 陈自强

(上海交通大学 海洋工程国家重点实验室； 高新船舶与深海开发装备协同创新中心， 上海 200240)

符号说明

A，B，C，D—系统矩阵

a1，a2，a3—RLS待辨识参数向量

C1—极化电容

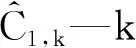
Ca—电池的额定容量

Cb—电池比热容

dUOCV/dT—开路电压温度系数

ek—k时刻端电压估计残差

h—对流换热系数

k—时刻

I—电流，充电为正，放电为负

Ik—k时刻的电流

Kk—k时刻的卡尔曼滤波增益矩阵

L—拉普拉斯变换

m—电池质量

OCVk—k时刻开路电压的估计值

P0—RLS误差协方差阵的初始值

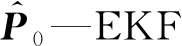
Pk-1—k-1时刻RLS误差协方差矩阵

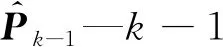
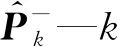
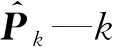
p0-p5—五阶多项式拟合系数

Qt—总热量

Qd—散热量

Qi—不可逆热

Qr—可逆热

R0—欧姆内阻

R1—极化内阻

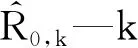
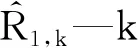
R-决定系数

S—电池表面积

SSR—回归平方和

SOC—锂离子电池荷电状态

SOC0—锂离子电池荷电状态初始值

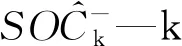
s—复频域变量

T—采样周期

Ta—环境平均温度

Tb—电池平均温度

Tbs—电池平均温度估计值

Tbs,error—电池平均温度估计误差

Tbmax—电池最高温度

Tbmin—电池最低温度

t—当前时间

t0—工况开始时间

t1—工况结束时间

U1—一阶电容电阻网络上的压降

Ut—锂离子电池的端电压

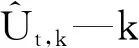
UKF—无迹卡尔曼滤波

UOCV—锂离子电池的开路电压

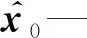
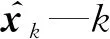
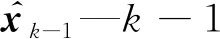
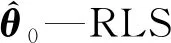
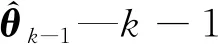
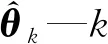
λ—遗忘因子

τ—时间常数

Φk-1—k-1时刻测量矩阵估计值

Φk—k时刻测量矩阵估计值

锂离子电池具有能量密度高、循环寿命长等优点，在新能源市场中占据越来越多的市场份额[1].然而，锂离子电池的温度对其内阻、老化等方面有着不同程度的影响.电池温度过高时将会造成老化程度加剧、内阻增大等问题，严重时还会导致热失控等后果.在以往的电池管理系统中，多是采用多路温度采集模块对锂离子电池温度进行实时监控.然而，在实际使用过程中，由于电压和输出功率的需求，往往需要将很多个单体电池串联或者并联在一起，此时对锂离子电池组进行温度监测往往要占用较多资源且局部采样温度无法代替整体温度，无法保证对锂离子电池热状态监控的准确性.为此，建立准确的锂离子电池在线温度估计模型对于锂离子电池热状态估计及热管理系统开发具有重要的意义.

为了准确地对锂离子电池进行热状态估计，需要得到锂离子电池在工作过程中的产热量.Wang等[2]利用绝热加速量热仪对锂离子电池在恒流充放电工况下产生可逆热与不可逆热进行测量，虽然实验结果较为精确，但是受实验环境影响较大.王腾[3]分析了锂离子电池的产热、传热及散热规律，结合计算流体力学软件分析了电池在时间域和空间域上的温度分布.孙金磊等[4]在恒温条件下采用了拓展卡尔曼滤波方法实时在线估计模型参数并结合传热学原理对电池温度进行估计，温度估计误差为1℃，然而对低温及变温环境下锂离子电池热状态估计未进行进一步研究.本文提出了一种基于递推最小二乘与拓展卡尔曼滤波相结合的可变环境温度下锂离子电池平均温度估计方法并在不同的对流换热环境下进行实验验证.

1 电池建模

1.1 等效电路模型

电化学模型与等效电路模型是常用的两类电池模型.其中，电化学模型从电池内部化学反应出发，以偏微分方程来描述电池特性[5]，虽然计算结果较为精确，然而考虑到实际应用过程中的计算复杂度及实验设备支持问题，等效电路模型相比于电化学模型更加具有优越性.因此，本文选择如图1所示的一阶等效电路模型对锂离子电池在工作过程中进行参数辨识与状态估计.R0模拟电池内部的接触内阻，一阶电容电阻网络用于描述电池在工作过程中的极化效应.则基于等效电路模型与基尔霍夫电压和电流定律可得到其微分方程：

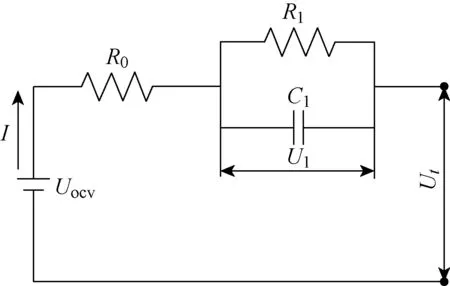
图1 一阶RC等效电路模型

(1)

Ut=Uocv-U1-IR0

(2)

电池的荷电状态(State of Charge，SOC) 常用来反映电池的剩余容量状态，其定义为电池剩余容量占电池容量的比值[6]：

(3)

1.2 热模型

锂离子电池在实际工作过程中的主要产热包括可逆热、极化热、欧姆热、有机电解液分解热及固体电解质界面膜分解热[7].其中有机电解液分解热和固体电解质界面膜分解热在电池正常工作范围内很小，只有在80 ℃以上时才急剧增加，因此锂离子电池的产热量可表示为[8]

(4)

Qi(t)=I(Uocv-Ut)

(5)

其中，可逆热为正值时对应吸热反应，负值时为放热反应，不同SOC及不同工况下可逆热的大小及正负号均有变化.电池的温度变化与电池生热及散热条件有关，电池的散热可以分为传导散热和辐射散热两部分，其中辐射散热在总散热量中占比很小，可以忽略不计[9]，则电池在单位时间内的散热量为

Qd(t)=hS[Tb(t)-Ta(t)]

(6)

2 电/热特性参数辨识

2.1 电气特性参数辨识

2.1.1OCV-SOC曲线 锂离子电池的开路电压(Open Circuit Voltage, OCV)是SOC的非线性函数.图2所示为常温25 ℃下10 A·h镍钴锰酸锂电池的OCV-SOC特性曲线.

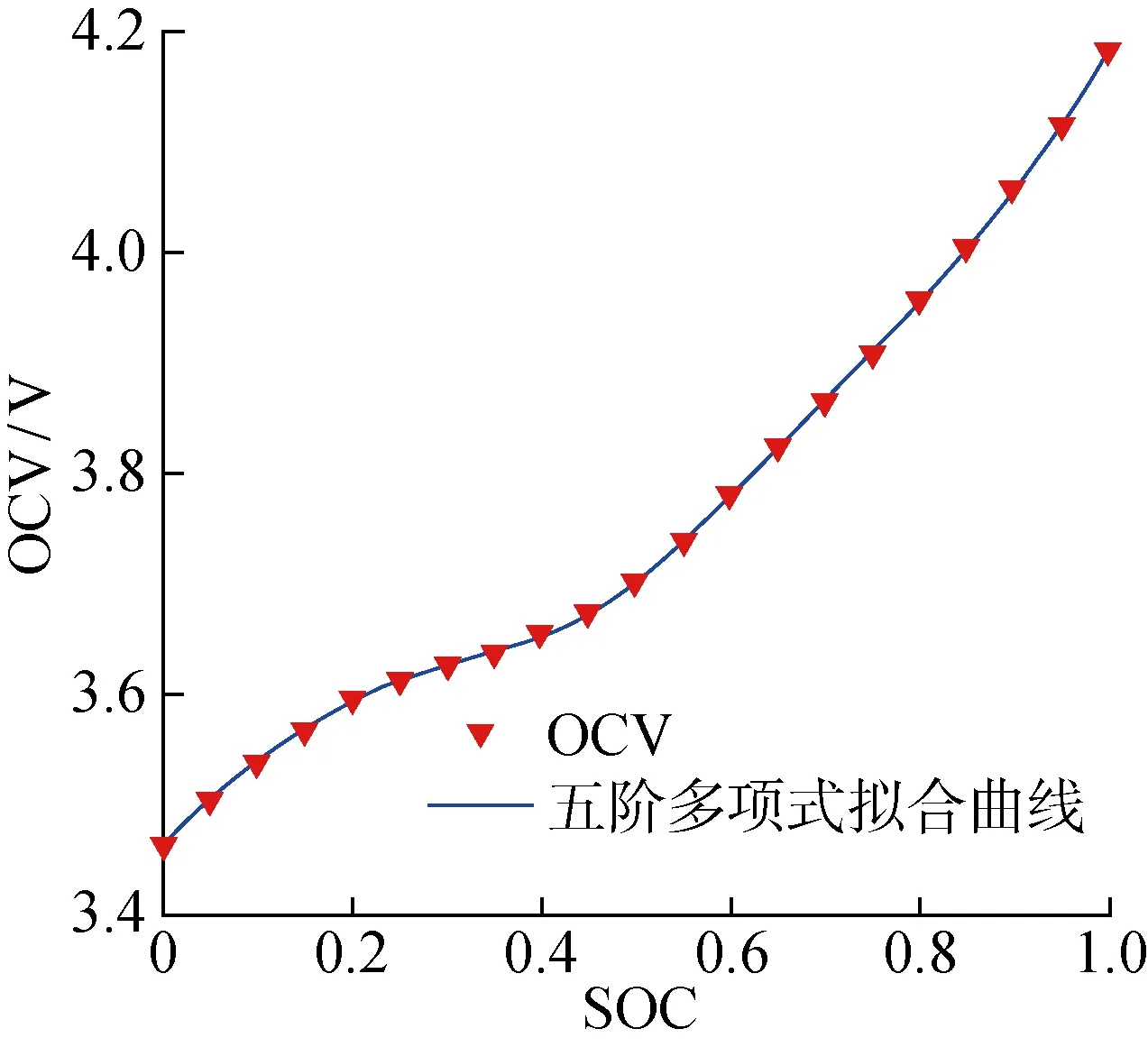
图2 25 ℃下OCV-SOC曲线

采用五阶多项式可以精确地拟合OCV随SOC的变化，拟合结果如表1所示.

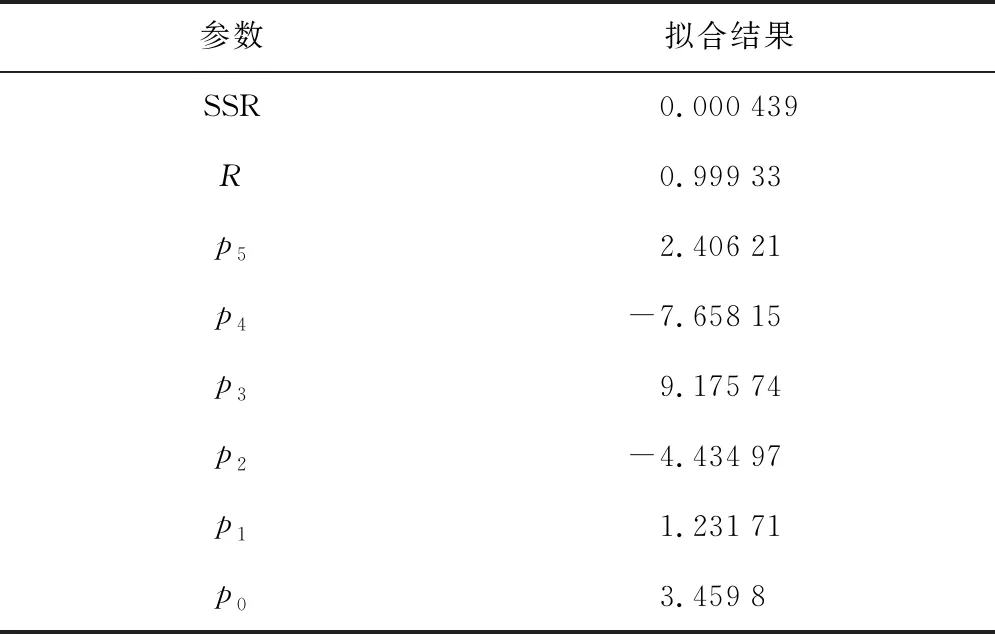
表1 五阶多项式拟合结果

f(SOC)=p5SOC5+p4SOC4+p3SOC3+

p2SOC2+p1SOC+p0

(7)

式中：p0～p5为拟合系数.

2.1.2一阶等效电路模型辨识 由自适应滤波理论发展而来的递推最小二乘算法可以利用实时测量的电池端电压与电流数据对等效电路模型进行迭代更新，不需要系统的先验统计知识，数据量小，适用于参数在线辨识.随着数据量的增长，会出现数据饱和的现象，在引入遗忘因子(Forgetting Factor，FF)后对性能指标中的每个时刻模型残差的平方进行指数加权可以降低历史数据对参数更新的影响.将式(1)代入式(2)，并进行Laplace变换可得到电池模型的传递函数[10]：

(8)

再对s域的输出方程进行双线性变换，得到z域下电压、电流及模型参数之间的关系式，令s=2(1-z-1)/[T(1+z-1)]，得到传递函数的离散形式：

G(z-1)=

(9)

τ1=R1C1

(10)

将上式转换为离散时间形式可以得到递推最小二乘(RLS)可以识别的自回归滑动平均(ARMA)模型：

(Ut-Uocv)k=a1(Ut-Uocv)k-1+

a2Ik+a3Ik-1

(11)

(12)

2.2 热特性参数辨识

2.2.1比热容 锂离子电池的比热容测试需要在绝热环境下进行，为此本文基于环境温度与电池温度跟随的控制策略搭建绝热实验环境[11]，脉冲工况下锂离子电池在工作过程中的产热将全部转化为自身的内能，电池的等效比热容可以根据Bernardi等[12]的发热功率计算公式获得.将电池置于绝热的环境中，电池产生的热量和吸收的热量相等[2]，则锂离子电池的热平衡方程可以表示为

(13)

由上式可以得到电池比热容为 1 128.33 J/(kg·K)，实验所用锂离子单体电池的其他主要参数如表2所示.

表2 单体电池主要参数

2.2.2开路电压温度系数 由式(5)可知，在已知电池电流和电池温度的前提下，要测得锂离子电池的可逆热只需测得dUocv/dTb[13]即可.为此本文采用平衡电位法[14]测得电池的开路电压温度系数，测量结果如图3所示.

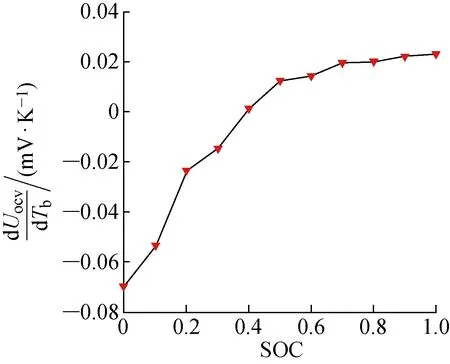
图3 dUocv/dTb-SOC特性曲线

3 自适应状态估计

3.1 SOC估计

拓展卡尔曼滤波(Extended Kalman Filter, EKF)算法广泛地应用于锂子电池的SOC估算中，该方法以线性最小方差为准则，能够有效地过滤系统噪声与观测噪声.基于电池等效电路模型的EKF算法通过求解雅克比矩阵，计算量相对较小，则系统的状态方程如下[15]：

xk=Axk-1+BIk-1+wk-1

(14)

Ut,k=f(SOCk)+U1,k+IkR0+‖vk‖

(15)

(16)

(17)

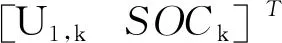
3.2 温度估计

经以上分析可以得到关于电池温度的线性微分方程：

(18)

如果电压和电流的采样周期相同，可以对连续时间系统进行离散化处理.在一个采样周期内对上式的等号左右两边都进行拉普拉斯变换得到如下结果：

(19)

令t0=kT,t=(k+1)T,k=0,1,…,整理可得：

Tb[kTb(s)]

(20)

对上式进行拉普拉斯反变换得到锂离子电池在工作过程中离散时间温度递推公式：

(21)

基于RLS-EKF算法锂电池平均温度估计流程如图4所示.

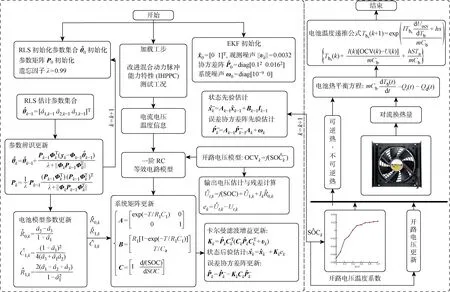
图4 基于RLS-EKF算法的锂电池平均温度估计流程图

4 实验验证与分析

4.1 实验设备

实验过程中主要用到的设备由锂离子动电池电气特性测试系统、可逆热测试系统及比热容测试系统组成，如图5所示.其中锂离子动力电池电气特性测试系统由上位机、BTS 4000电池测试平台及辅助通道等组成.锂离子电池可逆热测试系统由恒温箱、温度传感器及电压采集装置组成.比热容测试系统由锂离子动力电池、绝热实验箱、PID自整定温度控制器及上位机及温度传感器组成.采用风冷强制对流换热的方法让电池与电池箱内的空气进行热交换.为了对锂离子电池温度进行动态监控，在电池表面布置8个温度传感器T1～T8，详细位置如表3所示.其中，T1～T6的平均值作为电池的平均温度，T7～T8的平均值作为环境的平均温度.

图5 主要实验设备

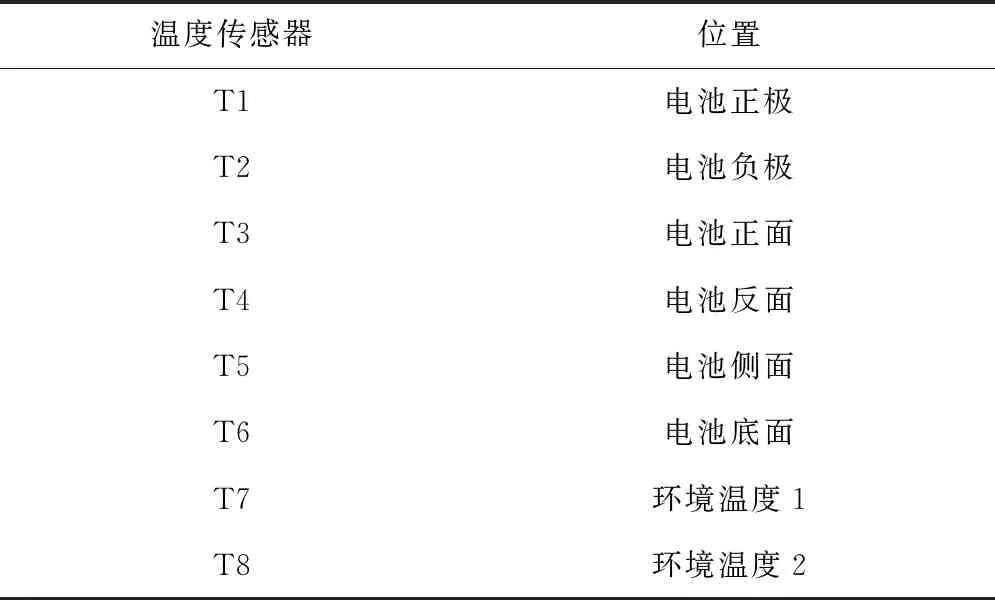
表3 温度传感器布置位置

4.2 可变环境温度下改进混合动力脉冲能力特性(IHPPC)测试工况

为了验证算法的实时性与准确性，本文使用改进混合动力脉冲能力特性测试工况进行实验验证，电池的初始状态为0.9SOC，当电池放电电压达到3.0 V时停止实验.电池的端电压与电流同步采样，采样时间为0.1 s，实验过程中电流、电压及温度随时间的变化曲线如图6和7所示.

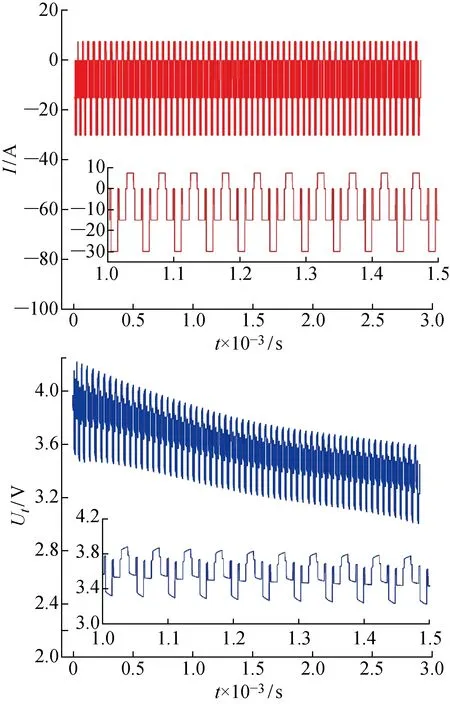
图6 IHPPC测试工况下电流电压变化曲线

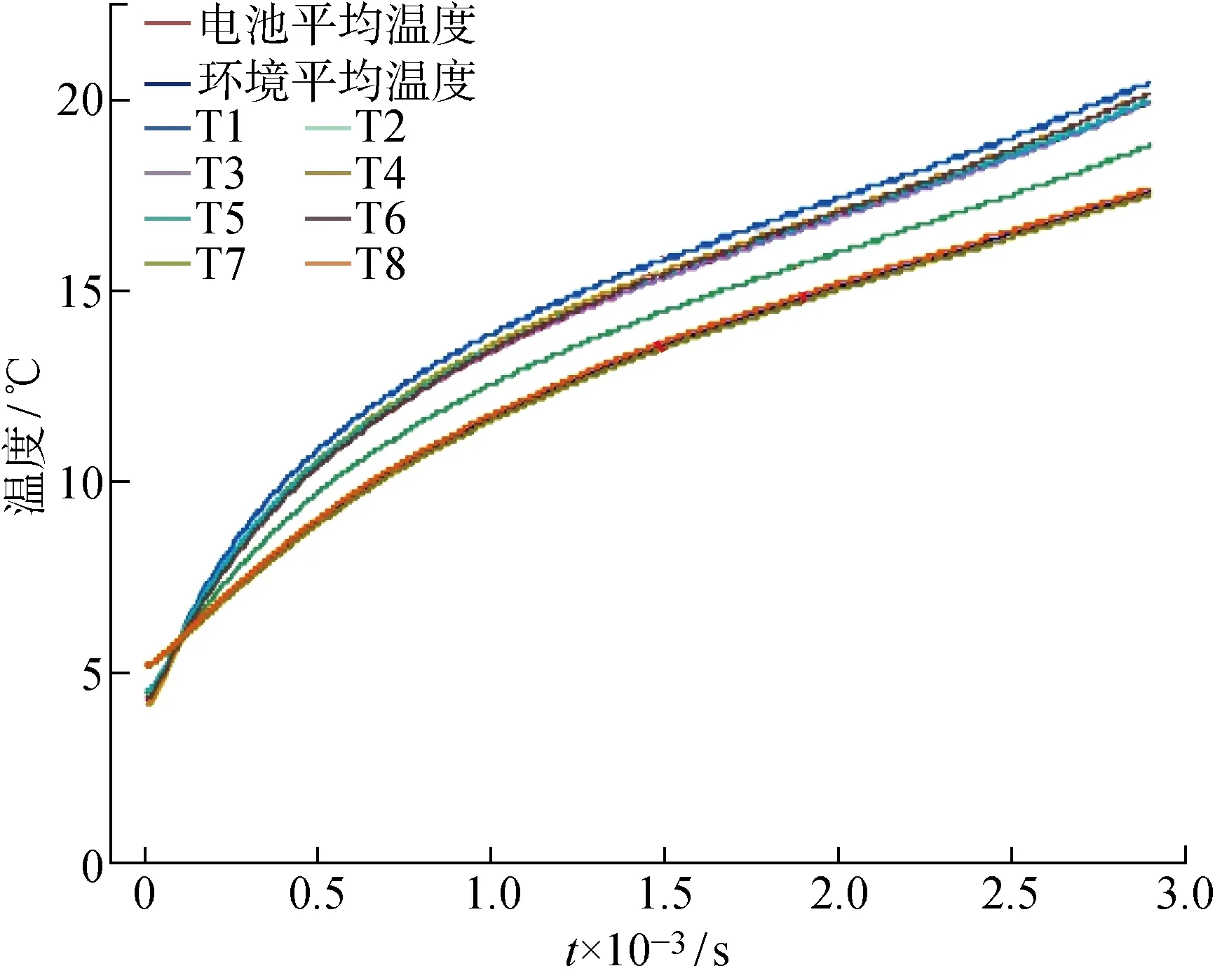
图7 IHPPC测试工况下温度变化曲线

4.3 状态估计结果与分析

图8所示为基于递推最小二乘算法得到的一阶等效电路模型参数辨识结果，其中一阶等效电路模型中参数的初始值由离线辨识结果得到.由图可知，相比于极化内阻，欧姆内阻受温度影响较大，且欧姆内阻和极化内阻的大小与电流大小有关.

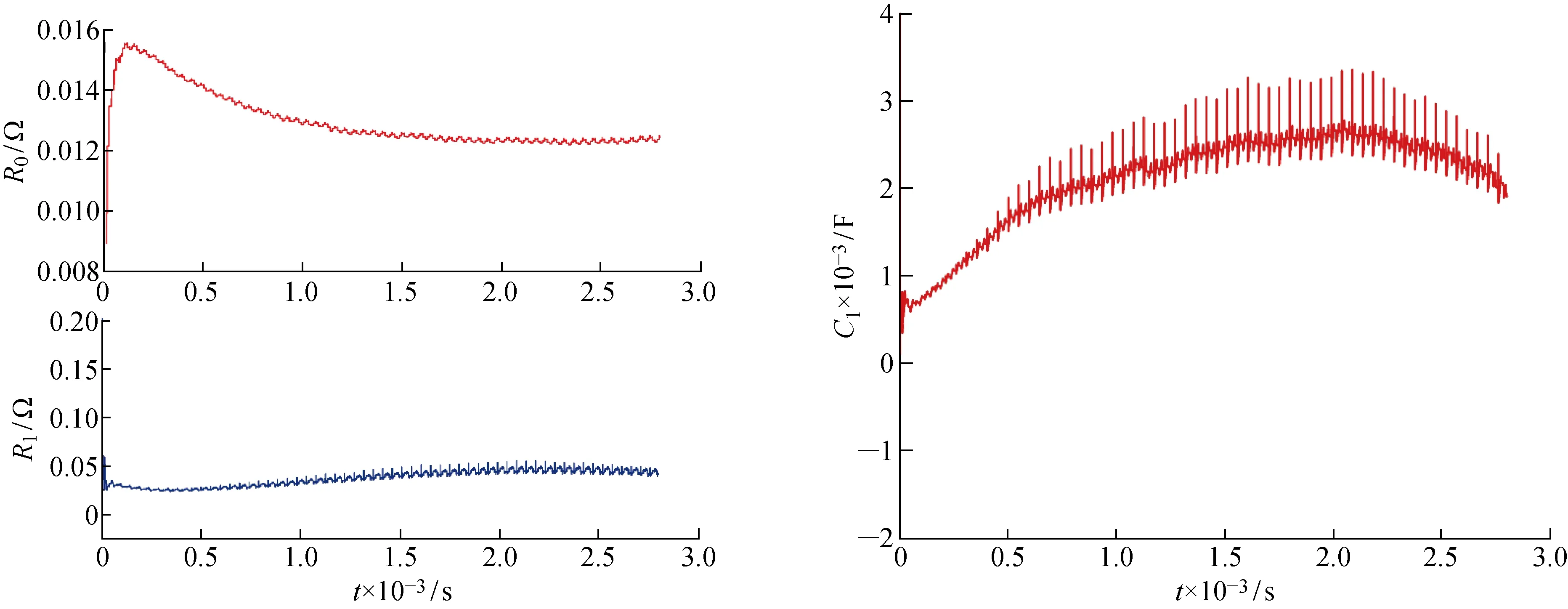
图8 电气参数辨识结果

图9所示为SOC的估计结果与误差.由图可知，相比于定值EKF，本模型可以在时变环境温度下对等效电路模型参数进行实时更新并能够准确地跟踪锂SOC的真实变化情况.当SOC的初始值分别取0，0.2，0.4，0.6，0.8时，该算法的稳健性较好，可以快速地收敛到真实值附近.

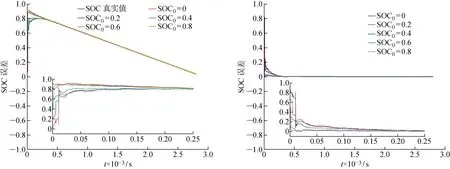
图9 SOC估计结果与误差

图10所示为锂离子电池在工作过程中产生的可逆热与不可逆热辨识结果.由图可知，锂离子电池在工作过程中单位时间内产生的不可逆热远高于可逆热，且在整个过程中不可逆热始终为正值而可逆热的正负号随着电流的正负及SOC的变化而变化.随着锂离子电池SOC的降低，可逆热先为负值后为正值，可逆反应先为吸热反应后为放热反应.

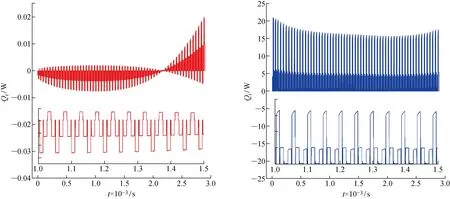
图10 可逆热与不可逆热辨识结果

由式(6)可知，锂离子电池的单位时间散热量与对流换热系数有关.为此，本文在不同对流换热系数情况下对所提方法进行实验验证，结果如图11～13所示.由图可知，本文中所提出方法能够在不同对流换热情况下对锂离子电池整体平均温度进行评估.电池的初始温度分别为25，20，15，10，5 ℃时，算法均在200 s左右收敛，且收敛后最大误差为1.8 ℃，平均误差仅为1 ℃.

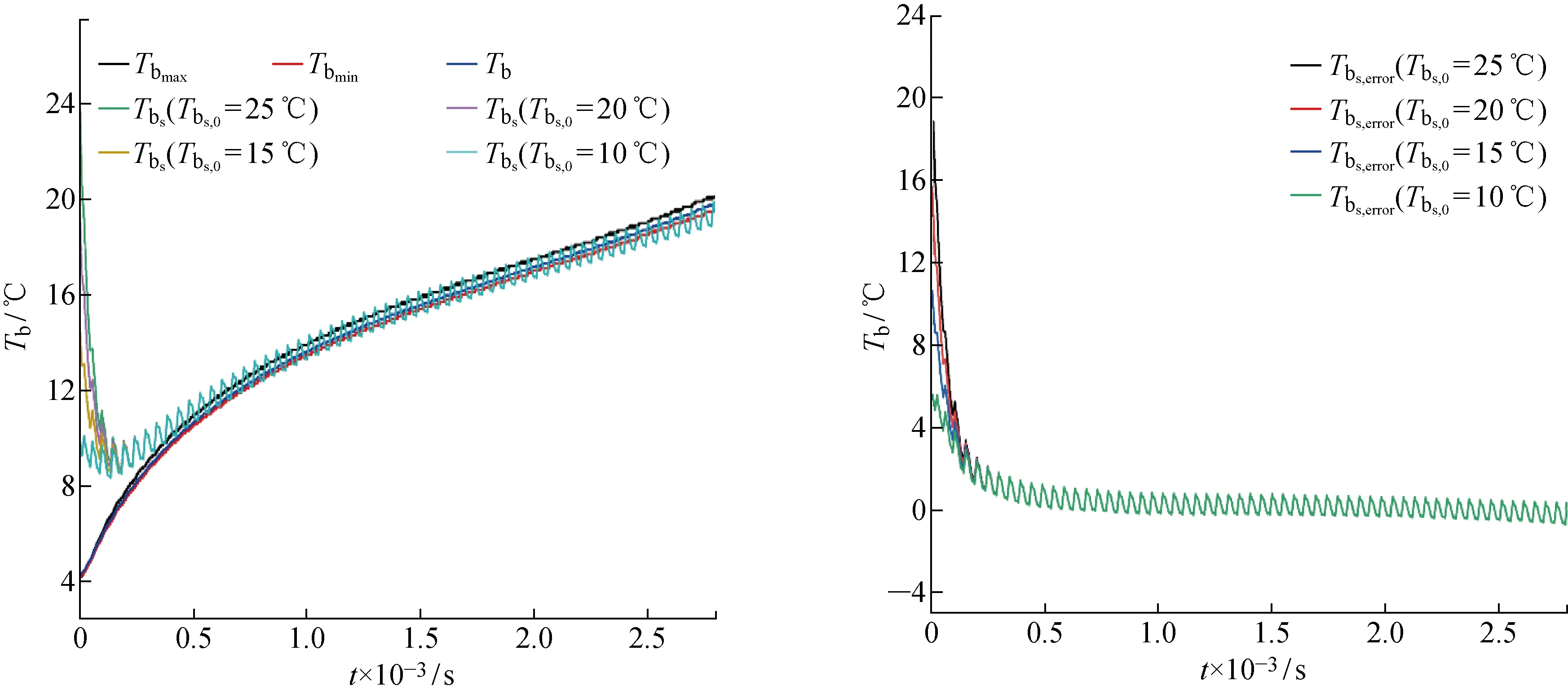
图11 低档风冷对流换热下Tb估计结果

以上分析表明， 本文中所提方法可以适用于不同对流换热条件下的锂离子电池平均温度估计，为了比较本文中所提方法的优越性，表4给出了不同算法下的估计结果.结果表明本文中所提方法在估计精度和收敛速度上均具有一定的优势.

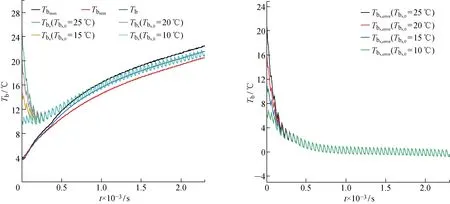
图12 中档风冷对流换热下Tb估计结果

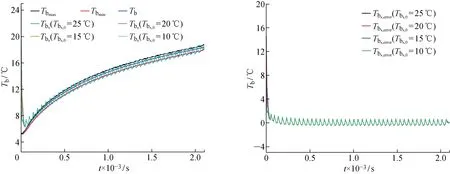
图13 高档风冷对流换热下Tb估计结果

表4 不同算法下估计结果

5 结语

本文中所提的方法能够在可变环境温度下对锂离子电池的平均温度进行估计，该方法可以时更新模型参数，算法收敛后对SOC的估计精度较好，均方根误差为0.274%，最大误差仅为1.070%.实验结果表明温度估计结果与实际测量结果一致，算法收敛后最大误差为1.8 ℃，平均误差仅为1 ℃.故本文中所提出的方法能够准确评估锂离子电池整体温度，有效地解决了因传统温度传感器布置方式所导致的局部温度无法代替整体平均温度的问题，为锂离子电池热管理技术开发提供了一定的理论和数据支持.