定量分析左心室射血运动特征的追踪方法设计
2021-08-02郑南南林剑圣
郑南南,黄 钢,林剑圣
(1.上海理工大学医疗器械与食品学院,上海 200093;2.上海健康医学院,上海 201318)
0 引言
心血管疾病(Cardiovascular Disease,CVD)是全球最常见的非传染性疾病[1]。我国心血管疾病发生率与死亡率正处于上升阶段,其中死亡率位居各类疾病首位[2],如何有效预防和诊疗心血管疾病成为重大公共卫生问题。
左心室射血运动为全身输送营养物质,是心脏功能的重要组成部分,异常的左心室运动提示可能患有心血管疾病,如冠脉梗塞引起的心肌供血不足会导致左心室射血无力。先进的医学成像技术,如心脏超声(Cardiac Ultra⁃sound,CU)、计算机断层扫描(Computed Tomograph,CT)以及心脏电影磁共振成像(Cardiac Cine Magnetic Resonance Imaging,CCMRI)等为医师提供了动态观察左心室是否正常运动的手段。然而,仅靠观察心脏运动状态诊断心血管疾病尚显不足,科研工作者正致力于准确量化心脏图像中左心室运动的研究。Valizadeh 等[3]在形变配准中引入心内膜形状信息以提高配准精度,但该法仅测量了左心室径向应变,对左心室完整运动的量化不够充分;Leong 等[4]结合钆增强和标记的磁共振图像融合信息分析心肌梗死患者的左心室运动,然而被标记的磁共振图像时空分辨率不高,较少应用于临床诊断心血管疾病;Mantilla 等[5]通过字典学习方法对左心室正常与异常运动进行分类,但该法不能导出左心室的运动细节,如位移场信息等;Qiao 等[6]分别采用传统配准方法与新兴卷积神经网络(Convolutional Neural Network,CNN)追踪左心室运动,与传统配准方法相比,当训练数据与测试数据来自相同健康志愿者时,CNN表现出更高的运动估计精度。然而CNN 评估心脏病患者左心室运动的准确度并不高,需要加入更多患者数据加强其泛化能力。目前基于像素灰度学习的左心室运动追踪比较困难,因为如果不考虑模拟数据,真实的左心室运动场几乎不可能获取。Tuyisenge 等[7]利用非线性光流法恢复左心室二维运动场,由于左心室心肌具有大尺度形变的特点,光流估计中的小运动假设并不符合左心室的运动事实。
针对以上问题,本文设计了一个通用左心室运动追踪框架,可用于不同心脏成像模态。该框架不需要对各类心脏疾病数据进行学习,能依据左心室轮廓特征,快速恢复像素级左心室位移场,详细展示左心室的运动细节。此外,该框架还可根据求得的位移场信息,分析左心室射血运动的各种量化参数,以便多角度辅助诊断心血管疾病。左心室运动追踪初始工作建立在心脏电影磁共振成像基础上,这是由于其具有无辐射、软组织对比度高、成像角度丰富等独特优势,广泛应用于临床。考虑到左心室轮廓丰富的形状属性能够为运动追踪提供可靠特征[8],本文首先利用三角网格构建左心室表面模型,该模型是轮廓点连通关系的表达;然后拟合轮廓点局部曲面,计算轮廓点弯曲能量;其次,基于映射准则估计所有当前帧轮廓点最可能的下帧位置,恢复初始轮廓位移场;最后,平滑优化轮廓位移场并计算左心室的位移和形变参数。
1 实验方法
拟建立一个基于心脏电影磁共振短轴图像的左心室运动追踪方法框架,恢复整个心动周期的左心室轮廓位移场。如图1 所示,整个方法流程主要包括4 个阶段:数据预处理、左心室表面模型生成、特征追踪和位移场优化。
1.1 数据预处理
数据预处理包括左心肌分割、轮廓平滑和插值。左心肌分割的目的为提取心内膜与心外膜轮廓,是本文的主要研究对象。目前常用的左心肌分割方法为图像驱动、主动轮廓模型和CNN[9-11]。本文采用CVI 心脏分析软件中左心肌分割功能获取的二值轮廓图像作为后续流程的基础图像。

Fig.1 Framework of motion tracking algorithm of left ventricle图1 左心室运动追踪方法框架
左心肌分割会因各类噪声,如图像质量差、左心肌周围组织干扰而得到不平滑轮廓。为确保运动追踪结果的可靠性,应消除局部尖锐的轮廓形状。为此,利用2 阶高斯平滑算法[12],使轮廓在整个心动周期的变化均趋于平滑。
由于覆盖心脏的电影磁共振短轴图像层间分辨率大于层内分辨率,因此在平滑轮廓后需要对短轴图像进行层间插值,以构造更为精细的左心室表面模型,有利于左心室的三维运动追踪。本文采用基于轮廓形状的插值算法[13-14],以弥补层间分辨率的不足。
1.2 左心室表面模型生成
将左心室各层面轮廓按照心尖到心底的顺序堆叠,并采用三角网格的方式连接相邻轮廓,由此生成左心室表面模型。狄洛尼三角剖分具有空圆性、最大化最小角等优良特性[15]。基于狄洛尼三角剖分思想,分两步构造相邻轮廓的三角网格:第一步是确定一组对称最近邻点对,该点对中任一轮廓点的欧式距离最邻近点均为点对中的另一轮廓点,如图2 左所示;第二步是以某个对称点对作为起始三角网格的两个顶点P1和P2,比较点P1与P4、点P2与P3的欧式距离,选择欧式距离更小的轮廓点作为第3 个顶点,至此一个三角网格构造完毕,如图2 右所示。该方法能构造出使所有三角网格边长总和最小的左心室表面模型。

Fig.2 Steps of construction of triangular mesh图2 三角网格构造步骤
对每个相邻轮廓均实施上述构网法则,便可得到左心室表面模型,如图3 所示。该模型能表达轮廓的局部形状属性,包括轮廓点与其邻域点的连通关系信息,为后续轮廓特征提取奠定了基础。

Fig.3 Surface model of left ventricle original contour(a)and interpolated contour(b)图3 左心室表面模型原始轮廓(a)与插值轮廓(b)
1.3 特征追踪
轮廓点与其邻域点形成的自然连通域是轮廓点局部形状属性的表征,如图4(a)所示。然而,自然连通域只是由有限个轮廓点构成的离散曲面。为了能较好地提取轮廓点局部形状属性,应对自然连通域进行局部曲面拟合。选择二元二次函数作为曲面拟合函数[16],表示为:

式中,x、y、z 为轮廓点坐标,a1~a5为需要求解的5 个逼近系数。采用最小二乘估计,以矩阵的形式表示,求得使逼近误差最小的系数向量a,表示为:

式中,A为n×5的矩阵,第i行每列元素分别为,n为构成自然连通域的轮廓点数目,z为轮廓点坐标值z的列向量。
计算出系数向量a后,便可以得到拟合的局部曲面,如图4(b)所示。根据求得的曲面函数,分析其曲面微分性质,选择最大主曲率k1和最小主曲率k2作为形状属性参数[17]。

Fig.4 Local surface fitting discrete surface(a)and continuous surface(b)图4 局部曲面拟合离散曲面(a)与连续曲面(b)
左心室运动会使轮廓产生弯曲变形,而主曲率能够度量轮廓的弯曲变形程度。将轮廓看作薄弹性板,弹性板的形变势能不受旋转与平移运动影响,仅由主曲率和弹性板的材料常数决定。具体表示为:

式中,εpo为轮廓点局部曲面势能,k1和k2分别为最大与最小主曲率,M为材料常数。
将轮廓点局部曲面势能映射到其邻域范围,得到轮廓的势能分布情况,如图5 所示。由图5 可知,左心室轮廓的整体势能较低,舒张期轮廓势能比收缩期更低,说明舒张期轮廓的形变程度更小。

Fig.5 Potential energy distribution of contours diastole period(a)and systolic period(b)图5 轮廓势能分布舒张期(a)与收缩期(b)
将轮廓点的局部曲面势能作为形状特征,根据映射准则进行特征追踪。该映射准则以轮廓在很短时间间隔内势能变化微小的假设为前提,表示为:
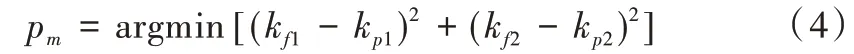
式中,kp1和kp2分别为当前帧轮廓点的最大与最小主曲率,kf1和kf2分别为下帧轮廓点的最大与最小主曲率,Pm为当前帧轮廓点的下帧匹配点,该匹配点为当前帧轮廓点位移范围内的最佳映射点。采用对称最近邻法确定当前帧轮廓点的下帧匹配范围[18]。
1.4 位移场优化
将匹配准则应用于每个当前帧轮廓点,得到轮廓初始位移场,如图6(a)所示。然而,单凭孤立的点到点匹配过程恢复的初始位移场在空间上没有局部相干性和整体协调性,这是由于当前帧轮廓点的匹配不受其他邻域轮廓点的约束,是一个空间独立过程,独立匹配得到的初始位移场并不符合左心室平滑的运动特征。因此,为了得到合理准确的位移场,需要对初始位移场进行平滑优化,表示为:

式中,μ和λ为平滑因子,d(p)ini为当前帧轮廓点初始位移向量,d(p)ave为邻域轮廓点的平均位移向量,d(p)smo1和d(p)smo2为平滑优化的位移向量。对每个当前帧轮廓点进行一定次数的两轮平滑迭代,便可以得到优化后的位移场,如图6(b)所示。

Fig.6 Displacement field of left ventricle original displacement field(a)and optimal displacement field(b)图6 左心室位移场原始位移场(a)与优化位移场(b)
2 实验结果与分析
2.1 实验数据
实验对象包括35 例女性和66 例男性,年龄14-88 岁,心率46~125 次/min,其心脏电影磁共振短轴图像数据均由GE1.5T 扫描仪通过稳态自由进动(Steady State Free Preces⁃sion,SSFP)序列获取。采集参数:图像矩阵大小为256×256,视野为360mm×360mm,重复时间为3.5ms,回波时间为1.4ms,层厚为6~7mm,层间距为7~10mm,可用于左心室运动追踪的帧数为20~28,层数为3~9。
2.2 实验结果
根据心脏电影磁共振短轴图像数据,首先计算101 例受试者的左心室射血分数(Ejection Fraction,EF),将其分为射血无力组(46 例,EF 小于50%)和射血正常组(55 例,EF大于50%),其中射血无力组EF 的均值和标准差为(0.377±0.093)%,射血正常组为(0.596±0.08)%。然后根据两组受试者收缩时期的左心室位移场导出左心室在径向、圆周方向上的最大累积位移、最高速度、最大累积应变和最高应变率。上述8 种描述左心室运动和形变特征的参数均由全局位移场计算得到,不再按照美国心脏协会(American Heart Association,AHA)的左心肌分段标准计算[19]。表1和表2 分别为两组受试者的全局峰值位移和速度,以及全局峰值应变和应变率。
Table 1 Comparison of kinematic parameters between normal EF group and weak EF group表1 射血正常组与无力组受试者运动参数比较 ()
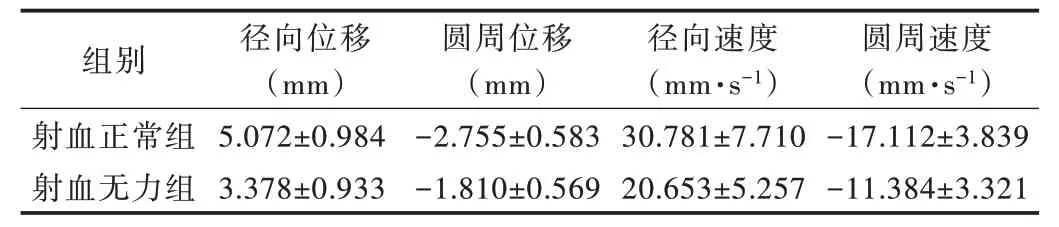
Table 1 Comparison of kinematic parameters between normal EF group and weak EF group表1 射血正常组与无力组受试者运动参数比较 ()
Table 2 Comparison of deformation parameters between normal EF group and weak EF group表2 射血正常组与无力组受试者形变参数比较()

Table 2 Comparison of deformation parameters between normal EF group and weak EF group表2 射血正常组与无力组受试者形变参数比较()
从表1、表2 中可以看出,射血正常组受试者运动和形变参数的绝对值均大于射血无力组,其中差距最明显的为圆周应变率(射血正常组为无力组的2 倍),其次为圆周应变(射血正常组为无力组的1.78 倍),射血正常组受试者其余各项参数均为无力组的1.5 倍左右。射血正常组EF 为无力组的1.58 倍左右,这说明射血分数越低,心力衰竭程度越高,从而导致左心室在径向和圆周方向的总体收缩幅度越小,总体收缩力度越弱。此外,左心室EF 与其运动、形变参数存在一定相关性,具体如表3 所示。

Table 3 The correlation between EF of left ventricle and parameters of motion and deformation表3 左心室EF 与运动、形变参数的相关程度
由表3 可知,EF 与左心室在径向、圆周方向上的运动和形变参数均具有较强相关性,其中相关程度最高的为径向位移(相关系数为0.878),说明EF 受左心室径向位移影响较大。这是由于径向位移描述的是左心肌在收缩阶段朝左心室中心运动的幅度,径向位移越大,左心肌朝室中心挤压得越厉害,左心室在收缩末期的体积越小,EF 也就越高。EF 正常受试者的左心室也可能存在运动异常情况,但本文计算的是整体位移场的运动与形变参数,未考虑局部节段的左心室运动。本文还对射血正常组和无力组受试者的各项运动与形变参数进行了差异性分析,以验证建立的方法能否判断左心室运动正常与否,具体如表4 所示。

Table 4 Difference of motion and deformation parameters between normal EF group and weak EF group表4 射血正常组与无力组受试者运动、形变参数差异程度
由表4 可知,两组受试者各项参数均具有非常显著的差异,说明本文方法求得的左心室位移场参数较为合理准确,能在一定程度上判断左心室是否正常运动。此外,为验证该方法的临床表现,将实验结果与CVI 软件进行同种参数相关性比较,该软件较为广泛地应用于临床心脏功能评估[20]。表5 为本文方法与CVI 软件各项参数的相关系数。

Table 5 Correlation analysis between the method and CVI software表5 本文方法与CVI 软件的相关性分析
由表5 可知,除圆周方向上的位移和速度外,本文实验结果与CVI 软件数据存在较高相关性,其中相关系数最高的为径向位移(0.814)。不同的运动追踪方法会因追踪策略或参数求解方式不同而存在差异,例如CVI 软件导出的圆周位移单位为弧度,而本文方法求取的圆周位移单位为毫米。进一步比较CVI 软件导出的射血正常组和无力组受试者圆周位移和速度的差异性,发现其差异系数分别为0.167 和0.029,不存在非常显著的差异。
3 结语
量化左心室射血运动能为临床诊断心血管疾病提供依据。本文首先利用三角网格生成左心室表面模型,形成轮廓点的连通网络关系;然后拟合轮廓点局部曲面,计算轮廓点的局部形状属性;最后通过映射准则恢复左心室位移场,并对初始位移场进行平滑优化。根据心脏电影磁共振短轴图像数据,将101 例受试者分为射血正常组和射血无力组,比较了两组受试者在径向、圆周方向上的位移、速度、应变和应变率,结果表明本文建立的方法能有效区分左心室是否运动正常。对本文实验结果与CVI 心脏分析软件数据进行相关性分析,发现二者存在较高相关性,或可为临床诊疗心血管疾病提供帮助。然而,由于难以找到合适且严格的标准描述位移场细节,对左心室位移场的验证仍存在一定难度和未知性[21]。
