融合朴素贝叶斯与决策树的用户评论分类算法

贾晓帆，何利力

（浙江理工大学 信息学院，浙江杭州 310018）

0 引言

随着互联网的飞速发展，为了满足用户需求，出现了网页、软件、手机应用等互联网产品，还包括建立在各类平台上而开发出的产品，如微信小程序、公众号等。用户在互联网中发表对产品的评价这一举动让用户从单一的信息接受者转变为互联网中文本信息的发布者，文本信息量呈指数级增长，仅仅由人工进行分析提取几乎不大可能，如何有效管理并充分利用这些信息值得思考。

朴素贝叶斯是机器学习的一个常用分类模型，模型本身是建立在贝叶斯定理和特征条件独立假设上的，有着坚实的数学基础，用概率统计知识对样本数据集进行分类。1990 年，Kononenko 等［1］证明了朴素贝叶斯的有效性。朴素贝叶斯的优势在于能够很快地在训练集中建立起贝叶斯模型，但是在有些实际应用中分类效果却不尽如人意。因为在用贝叶斯分类的前提下，必须假设属性独立，即属性之间没有关系，当该假设不成立时，就会影响贝叶斯分类效果。为了解决该问题，学者们放松属性之间相互独立的条件假设，提出了贝叶斯网络分类器［2］，其基本思想是考虑全部或者部分属性之间的关联性，以此满足朴素贝叶斯模型相互独立的条件假设。尽管这种思想能提高分类性能，但是在训练中需要测算所有属性之间的相关性，导致算法复杂度剧增。1996 年，Sahami［3］提出K-依赖贝叶斯分类器，有效提升了分类性能；1997 年，Friedman 等［4］提出了一种树扩展的朴素贝叶斯分类器，简称TAN 模型，它在测算属性之间相关性的基础上，构建树形结构图；1999 年，Nurnberger 等［5］提出了基于神经模糊的朴素贝叶斯分类器，简称BAN 模型，它是TAN 模型的升级版，相比TAN 模型，允许特征属性之间形成有向结构图；2004 年，Wang 等［6］提出基于自适应的Boosting 与朴素贝叶斯结合方法，可以有效地缓解噪声提高分类性能；2008 年，徐光美等［7］通过基于互信息计算各属性与各类别之间的相关性，选择不相关的特征值代入朴素贝叶斯模型中；2011 年，Zheng 等［8］通过删除一部分相关性强的特征属性，将处理后的特征属性应用于朴素贝叶斯分类模型；2014 年，杜选［9］提出一种基于加权补集的朴素贝叶斯文本分类模型，这种模型可避免在训练集不平衡时，可能导致分类性能低的缺陷。

本文在研究朴素贝叶斯算法的基础上提出一种与决策树相融合的算法，使用本文算法可以有效填补数据集中的缺失属性值。实验结果证明，本文算法的分类效果比传统朴素贝叶斯分类效果更好。

1 理论基础

1.1 Laplace 方法

Laplace 是最古老的平滑技术之一，所谓平滑技术是指为了产生更理想的概率以调整最大似然估计的技术［10-11］。计算公式如下：

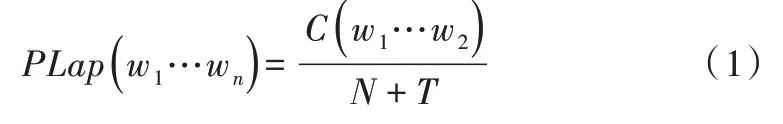
其中，N 为训练实例总数量；T 为训练集实例种类数。在Laplace 估计中，先验概率P（Y）被定义如下：

其中,nc是满足Y={yj} 的实例个数，N 是训练集个数，n是类的个数，并且k=1。

1.2 朴素贝叶斯

朴素贝叶斯分类（NBC）是一种假设特征与特征之间相互独立的算法，它基于贝叶斯定理，算法逻辑稳定且简单，朴素贝叶斯的健壮性较好，其分类功能在数据展现出不同特点时，差别不大，也即在不同类型的数据集中不会表现出太大差异［12］。因此，当数据集属性之间的关系相对独立时，朴素贝叶斯分类算法会有较好的效用。

（1）贝叶斯定理。根据条件概率可知，事件A 在事件B已发生的条件下发生概率为：

同样地，在事件A 已发生条件下事件B 发生的概率为：

结合两个方程式可以得到：

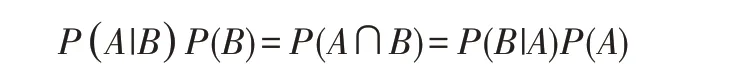
上式两边同除以P（A），若P（A）为非零，可以得到贝叶斯定理：

（2）朴素贝叶斯定理。设有样本数据集D={d1,d2,…,dn}，对应样本数据的特征属性集为X={x1,x2,…,xd}，有类别集合Y={y1,y2,…,ym}，即D可以分为ym类别。其中x1,x2,…,xd相互独立且随机，则Y的先验概率P=P(Y)，Y的后验概率P=P(Y|X)，由朴素贝叶斯算法可得后验概率为：

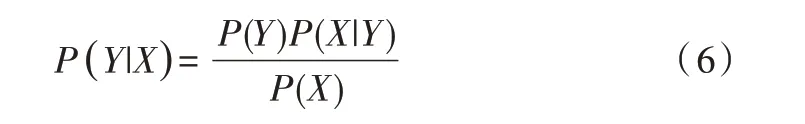
朴素贝叶斯基于各特征之间相互独立，在给定类别为y的情况下，式（6）可以进一步表示为：

由式（7）可计算出后验概率为：

由于P(X)的大小固定不变，因此在比较后验概率时，只比较式（8）的分子部分即可。因此，可以得到一个样本数据属于类别yi的朴素贝叶斯计算公式如下：

1.3 决策树

决策树是一种包含根节点、内部节点、叶节点3 种节点的树型结构。当文本分类算法为决策树时，它由树的内部节点逐一标注所构成，叶节点表示对应的类别标签，与叶节点相连的分支上标注着其对应的权重，树的叶子节点表示文本分类目标，当从根开始遍历查询最终到达某一个叶子节点，这样就完成了一次文本分类［13］，树的高度就是时间复杂度，它是一个自顶向下、分而治之的总过程。决策树的准确率会因重复的属性而受一定影响，因而用决策树进行分类是要对数据进行特征选择。决策树在开始阶段会浪费时间，但只要模型建立起来，运用阶段非常快。

决策树算法是一种无监督分类方法，决策树的生成主要分为节点分裂和阈值确定，节点分裂指当一个节点所代表的属性无法判断时，则选择将一节点分为多个子节点，而选择适当的阈值可以使分类错误率最小。决策树以树的层次规则为特征，叶子节点为分类目标，通过遍历根节点到叶子节点完成一次分类操作。决策树分类算法与其他决策支持工具相比较起来易于理解和解释。然而，通过有限的数据集无法训练出可靠的类标签，并且对特征空间计算成本非常高，这对决策树而言是一种限制［13］。决策树算法作为一种常见分类算法，有很多变种，包括ID3、C4.5、C5.0、CART 等。其中，最常用的、最经典的是C4.5 算法。

2 改进思想

2.1 朴素贝叶斯概率优化

朴素贝叶斯的概率估计会在训练样本不足时出现零概率的问题，这会导致求出的类标签的后验概率值为零，使用连乘计算文本出现概率时也是零，传统的朴素贝叶斯在这种情况下无法进行分类，这一直以来都是朴素贝叶斯的难题。为了解决该问题，法国的数学家拉普拉斯（Lapla⁃cian）首次提出一种加法平滑方法，对每个词的计数加1，该加法平滑也叫拉普拉斯平滑。该方法基于一定的数学理论基础，在数据集较大的情况下，每一个词出现的次数加1之后对概率估计结果的影响可完全忽略不计，但是却可以有效地避免出现零概率问题。针对本实验所采取的朴素贝叶斯模型，采用词频估算每一个特征，其经过拉普拉斯平滑方法处理后的表达式为：

2.2 朴素贝叶斯与决策树融合

为了提高贝叶斯分类准确性，在提出的贝叶斯与其他方法相结合的算法中，最为代表的是Kohavi［14］提出的NB⁃Tree 算法。对于大型数据分类，决策树和朴素贝叶斯相比，前者在维度较大或者属性之间的依赖关系明显优于后者，后者的分类结果准确性优于前者。而NBTree 算法刚好结合贝叶斯和决策树各自的优点，提升了算法效率。

C4.5 算法的优点是产生的分类规则易于理解，准确率较高，C4.5 经过树生成和树剪枝建立决策树。在计算每个属性的信息增益率（Information GainRatio）后，选出信息增益率最高的属性对给定集合测试属性，再采用递归算法根据测试属性建立分支，初步得到决策树。

在用决策树对测试样本数据进行分类时可能会有某些属性值缺失，传统的决策树算法在面对这些缺失的属性值一般会采用抛弃缺失属性值或者重新给定一个在训练样本中该属性常见的值［15］。而C4.5 算法会采用概率分布填充法处理缺失属性值，具体执行过程：首先为某个未知属性每个可能的值赋予一个概率，再计算某节点上属性不同值的出现频率，这些概率可以被再次估计［16］。C4.5 算法相关计算公式如下所示［17］。

（1）期望信息（也称信息熵）。设S是Si个数据样本的集合，假定类标号属性有m个不同值，定义m个不同类Ti(i=1,…,m)。设Si是类Ti中的样本数。对一个给定的样本分类所需的期望值为：

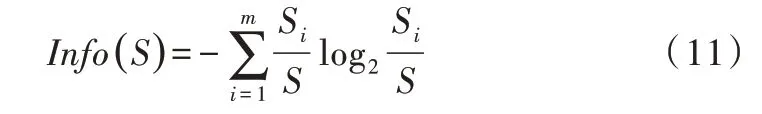
（2）信息增益。由属性A划分成子集的信息量为：

信息增益为原来的信息需求与新的需求之间的差。即：

（3）信息增益率。C4.5 算法中引入了信息增益率，属性A 的信息增益率计算公式为：

在决策树的剪枝阶段，C4.5 算法采用后剪枝技术形成决策树模型，根据建立好的模型生成一系列IF-THEN 规则，实现对训练集的分类。

C4.5 算法虽然在处理噪声方面有很强的能力，但是在训练集缺失属性值很高的状态下，使用C4.5 算法构建的决策树模型会变复杂并出现更多的结点数，最终分类准确率也会下降［18］。鉴于朴素贝叶斯分类具有坚实的理论基础、较小的出错率，本文提出一种基于朴素贝叶斯定理的方法［19］，以处理空缺属性值。

假定一个样本训练集D={d1,d2,…,dn}，每一个训练实例描述为di={di1,di2,…,dih}，对应样本训练的特征属性集A={A1,A2,…,An}，每个属性Ai的属性值是{Ai1,Ai2,…,Aih} 。训练集包含的类别集合C={C1,C2,…,Cm}，即D可以分为Cm类别。与训练集D 有关系的决策树有如下特点：①内部节点由Ai表示；②子节点属性与父节点属性用枝干相连；③叶节点由Ci表示。树被建立起来后对每个测试实例进行分类，实例di的结果就是一个类别。基本步骤为：一是用训练集构造一个决策树；二是将概率优化后的朴素贝叶斯运用到测试集D 中。

对于训练集D，首先运用决策树分类器对每个di进行分类。如果训练集中没有空缺属性，则将数据压入D1 集合，如果有，则按空缺个数压入D2 集合，数量越少越排前，到所有数据都检测完则结束，最后形成了D1 和D2 两个集合，其中D1 放入的是没有空缺属性值的数据集合，D2 放入的是包含空缺属性值的数据集合；读取D2 中的数据，用概率优化后的朴素贝叶斯处理空缺属性后放入D1 中，递归直到D2 集合中数据为0。处理完训练集D 中的空缺属性值后，再用决策树对更新后的训练集进行分类。

3 实验分析

3.1 实验数据

本文实验选取的是某互联网营销平台微信公众号中活动的91 120 条中文用户评论，通过考察用户评论，将数据分为积极和消极两类数据，并选用准确率和召回率评价分类效果。部分数据如表1 所示。

Table 1 Data of some user comments表1 部分用户评论数据

3.2 数据预处理与文本特征抽取

数据预处理包括3 个部分，即：文本正则化、切分成词和去掉停用词。运用TF-IDF 方法抽取数据特征，如表2 所示。

Table 2 Data preprocessing and text feature extraction表2 数据预处理与文本特征抽取

3.3 朴素贝叶斯与决策树分类融合

采用融合朴素贝叶斯和决策树的算法对用户评论进行分类，最终正确地将用户评论分为积极和消极两类，如表3 所示。

Table 3 Classification results表3 分类结果

本文实验结果采用准确率和召回率两个指标，计算公式如下：

其中，TP 表示正确的标记为正，FP 错误的标记为正，FN 错误的标记为负，TN 正确的标记为负［20］，如表4 所示。

Table 4 Parameter meaning表4 参数含义

最终计算得到的分类准确率和召回率如表5 所示。

Table 5 Analysis of experimental results表5 实验结果分析

由表5 可知，为了对比本文中提出的算法是否可行有效，通过对比朴素贝叶斯对用户评论的分类，本文算法准确率高出0.5 个百分点，召回率高出0.2 个百分点。由此可见，在用户评论文本分类中，融合朴素贝叶斯和决策树用户评论分类效果取得了不错的结果。

4 结语

为了实现对用户评论的商业研究价值提取，解决互联网产品后续优化和增进服务问题，本文提出了一种融合朴素贝叶斯与决策树的用户评论分类算法。该研究首先对文本正则化、切分成词并去掉停用词，再融合朴素贝叶斯和决策树算法，并将其应用于微信公众号互联网营销用户评论分类中，最终可以正确地将用户评论分为积极和消极两类。其中，积极的用户评论可以作为后续互联网营销活动优化，提升用户体验的重要参考依据，消极的用户评论可以增进自己的服务。对分类结果的分析表明，改进后的算法解决了朴素贝叶斯的零概率问题和决策树因属性值缺失率高导致的分类准确度下降问题，提高了分类准确率。由于数据集不足以及中文语义复杂，会造成评论分类出现相反的情况，后续要在语义情感特征准确性提取上作进一步研究。