三相并网电压逆变器的无源控制策略

许大伟，张会林

（上海理工大学 机械工程学院，上海 200093）

0 引言

在过去的几十年内，人们对能源的肆意挥霍导致环境破坏和全球气候变暖等国际性问题。新能源的崛起与发展在很大程度上减少了人们对传统石化能源的依赖程度，同时也减轻了环境污染。目前，开发可再生能源主要通过分布式发电系统（Renewable Energy based Distributed Power Generation System，RE-DPGS）进行［1］。在典型的RE-DPGS网络拓扑结构中，小型光伏发电、小型风光互补发电等各种可再生能源发电与燃料电池等储能单元经过电力电子变换器接入直流母线，然后通过集中DC/AC 逆变器和工频变压器后送入电网；或者首先经过电力电子变换器接入交流母线，然后通过电力变压器馈入电网。该逆变器通常被称为并网逆变器，其在RE-DPGS 中处于核心地位，并已得到广泛关注［1-2］。然而，并网逆变器通常会输出大量谐波，需要采取有效手段对其进行滤波后才能接入电网。为满足对输出电流谐波含量的要求，研究者们根据不同实际应用需求，先后探索了许多滤波方法，如L、LC、LCL 等滤波器。许多实验证明，与前两种滤波器相比，LCL 滤波器具有更好的滤波效果，特别是在处理高频谐波方面，其滤波电容支路会在高频谐波时呈现低阻抗，而滤波电感则会呈现高阻抗，如此将分流谐波电流，进一步抑制高频率谐波电流流入电网，提高电网的电流质量，因此LCL 滤波器拥有良好的滤波性能［3］。然而，LCL 滤波器存在的缺点也同样值得重视，即谐振频率存在较大谐振尖峰，容易发生振荡，可能会破坏系统稳定性，对电网产生较大负面影响［1-4］。

针对LCL 型滤波器的固有谐振特性，应采用合适的阻尼方法进行抑制，从而确保逆变器的稳定性，常用方法包括电网阻抗估算法［5］、固定阻尼法［6］、无源阻尼法和有源阻尼法［7-8］。然而，阻抗估算法在估算准确度、检测速度和抗能力干扰方面的缺陷限制了其广泛应用；固定阻尼法很难应用于多个谐振尖峰同时出现的情况；无源阻尼法虽然很容易实现，在工业中应用广泛，但其插入的一个或多个电阻器会产生额外功率损耗，降低系统效率；与无源阻尼相比，有源阻尼法虽然增加了算法控制的复杂性，却没有额外的功率损耗，而且拥有更好的衰减性能，是一种广泛应用的方法。

传统线性控制方法包括比例积分（PI）控制［9］、比例谐振（PR）控制［10］、重复控制［11］、预测控制［12］等，同时还有一些非线性控制方法，如滞环控制、滑模控制（SMC）、神经网络控制［13］等。这些控制策略均取得一定成效，但同时也存在一些缺陷，例如PI 控制器可能会存在抗干扰性和稳定性不足的缺点［14］。因此，本文介绍一种无源控制技术（Pas⁃sivity-Based Control，PBC），其基于能量分配控制，通过使用系统耗能特性进行阻尼注入的控制。首先建立三相并网电压逆变器（Grid-Connected Voltage Source Inverter，GCV⁃SI）的拓扑结构与欧拉—拉格朗日（Euler-Lagrange，E-L）数学模型，采用在系统中注入阻尼的方法设计PBC 控制器，理论上整个系统为无源的，如此便可保证系统的稳定性［15］，经过验证其动态性能也满足要求。

1 无源性理论

无源性作为研究非线性系统特性的常用手段，最早是由Lurie 和Popov 提出，后来得到研究人员的推广与发展［16］。无源性是从能量守恒的角度分析系统与外界之间能量流动的趋势，可以看作是耗散性的一个特例，反映运动系统能量的耗散特性。

假设在初始时刻系统储存能量E（t0），系统的耗散功率为pdiss≥0，如果对任意端口向量｛x，y｝，以及任意时刻t≥t0：

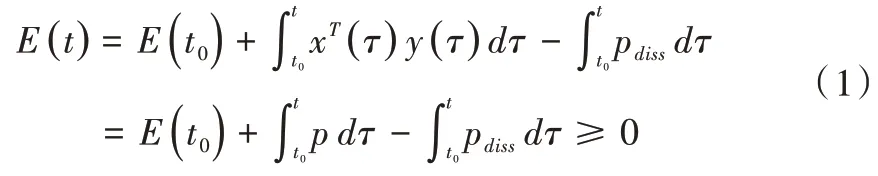
则该系统为无源的，且由式（1）可知，该方程是有下界的。若无源系统处在吸收能量的状态，则不作考虑。但是，当其向外释放能量时，需要对其加以分析，易得：

从式（3）可知，由于系统功率变化不能为无穷大，即等式左边能量E对时间t的二阶微分有界，dE/dt一致连续。E（t）满足类李亚普诺夫引理的条件，因此当时间t趋向于无穷大时，dE/dt→0，即有p-pdiss→0。由于耗散项的存在，系统对外界产生的能量输出最终为零。

综上可知，随着时间的推移，系统自身的能量E（t）终将会被耗散项拉向零的状态，这样系统将具有渐进稳定性。具体如图1 所示，其中P表示耗散的能量。

对于本文提出的三相GCVSI，可以通过系统输入导纳的无源性研究其稳定性。如果系统输入导纳的实部（也被称为电导）对所有频率均为非负，则可以保证系统是稳定的，这是由于无论网络如何复杂，仅由无源组件组成的网络总是稳定的。

Fig.1 Energy state of the system图1 系统能量状态

2 带有LCL 滤波器的GCVSI 数学模型

图2 为带有LCL 滤波器的系统结构图。定义输出电流和电网电压分别为I2k和Vgk（k=a，b，c），逆变器侧的输出电流和电网电压分别为I1k和Uk（k=a，b，c），L1和L2的寄生电阻分别为R1，R2，电容器的电流和电压分别为ICk和UCk（k=a，b，c），Zg为电网的阻抗（仅包括代表最坏条件的电感Lg），Vpcc为公共点耦合（PCC）的电压，N代表电压的参考点。应用基尔霍夫电压定律（KVL）和基尔霍夫电流定律（KCL）推导LCL 滤波的GCVSI 数学模型，即得到式（4）。为简化分析与判断，本文使用欧拉—拉格朗日（EL）模型。EL 模型是非线性PBC 理论的重要组成部分，是一种有效的建模方法。系统以a-b-c坐标描述，其中轴上的状态变量具有复杂的耦合。为避免该问题，此处采用d-q变换，见式（5），最终变换为α-β坐标系下的方程。

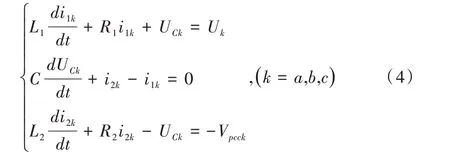
转换成d-q坐标系中的模型为：

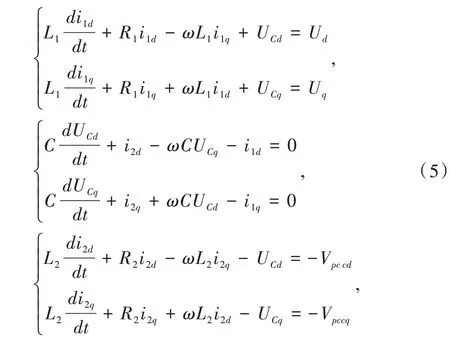
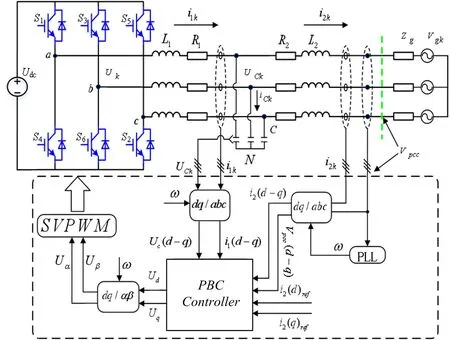
Fig.2 System structure图2 系统结构

选取状态变量并表示为矩阵的形式：

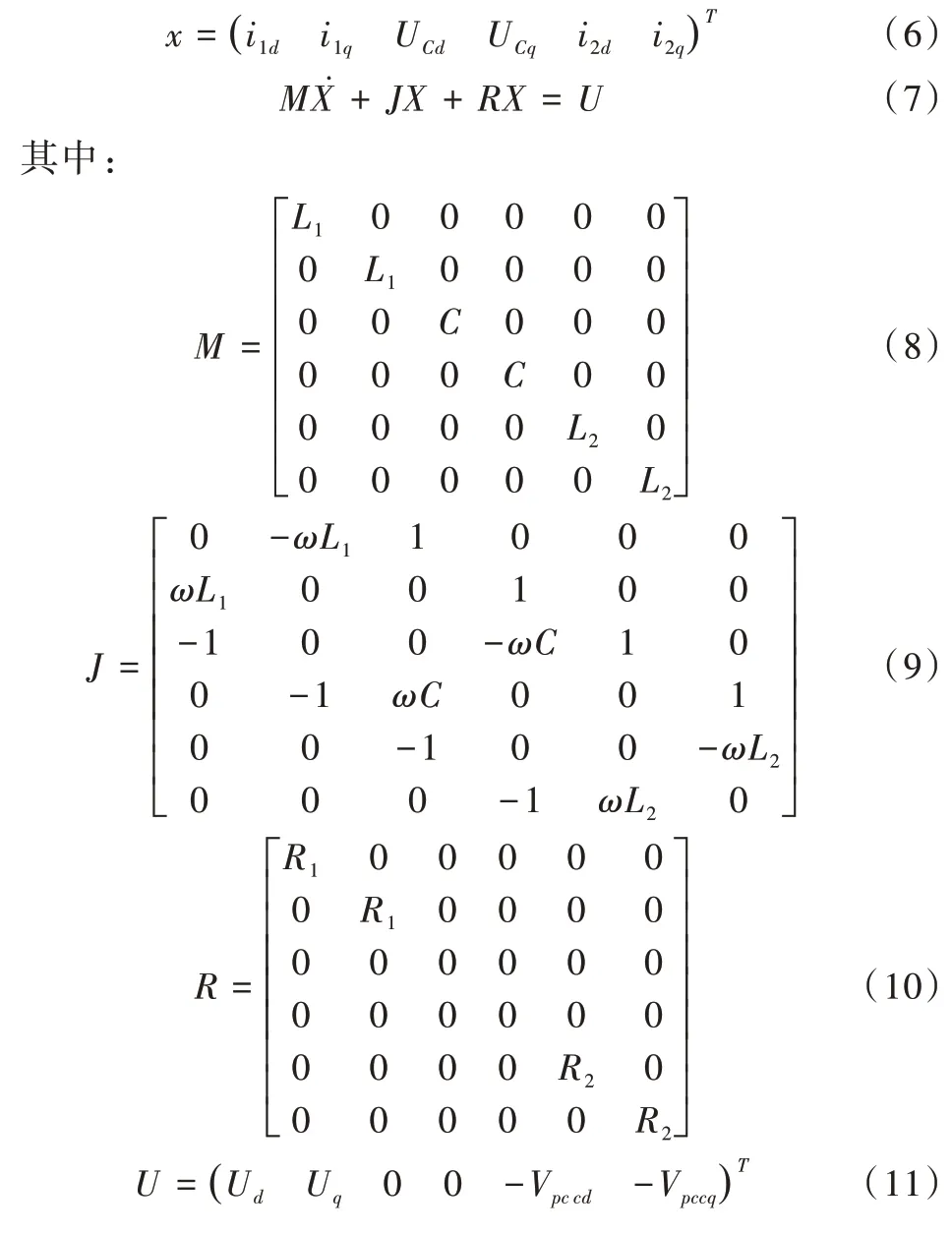
可以看到M为正定矩阵，M=MT；J为反对称互连矩阵，描述了不同状态变量之间的耦合关系，且J=JT；R为表示系统耗散特性的正半定矩阵；U为外部输入矩阵，描述了环境与系统之间的能量交换。

设系统存储的能量函数为：

由式（12）可得：

H（x）表示系统中L1、C、L2储存的能量，由上等式可以看出系统为耗散型的。

3 PBC 控制器设计

定义参考状态变量为：

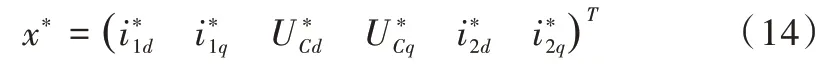
误差向量定义为：

因此得到误差EL 方程为：

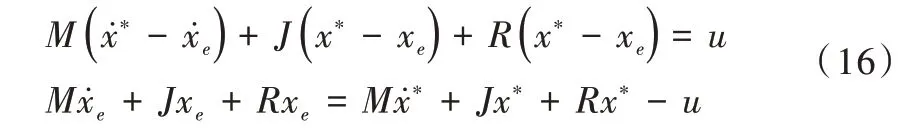
由式（12）可以得到系统的误差存储函数为：

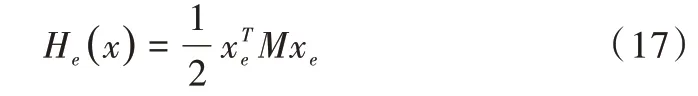
如果xe等于零，则会出现预期条件，此时：

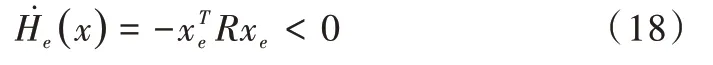
李亚普诺夫引理系统会渐进稳定，为加快收敛速度，可以将阻尼矩阵Rd添加到误差系统中，得到注入阻尼的矩阵与新的耗散矩阵为：

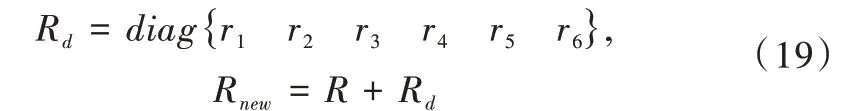
由于结构对称，r1=r2，r3=r4，r5=r6，新的误差方程可表示为：

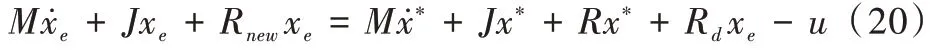
在稳定状态下，xe等于零，因此等式右边也等于零，这样便可得到控制律为：

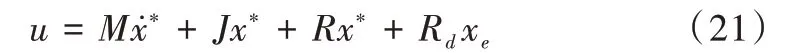
将状态空间表达式经拉普拉斯变换得到频域模型，构建控制框图，如图3 所示。

4 仿真验证

为验证基于PBC 控制器的三相并网电压逆变器理论的正确性，根据图2 的系统结构图，在MATLAB/SIMULINK上搭建了一个仿真平台。平台中采用的参数如表1 所示。

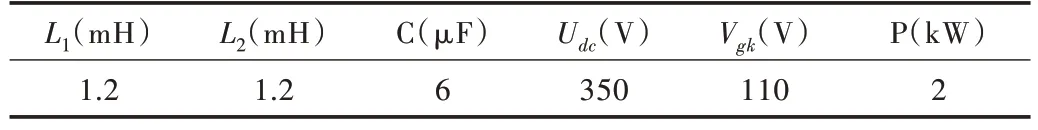
Table 1 SIMULINK simulation system parameters表1 SIMULINK 仿真系统参数

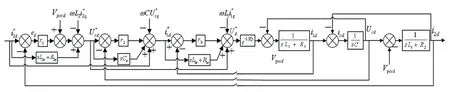
Fig.3 System control block diagram图3 系统控制框图

系统导纳实部为正，则能保证系统稳定，反之系统则不稳定。根据传递函数，利用Wolfram mathematica 软件调制3 组参数，具体如表2 所示。

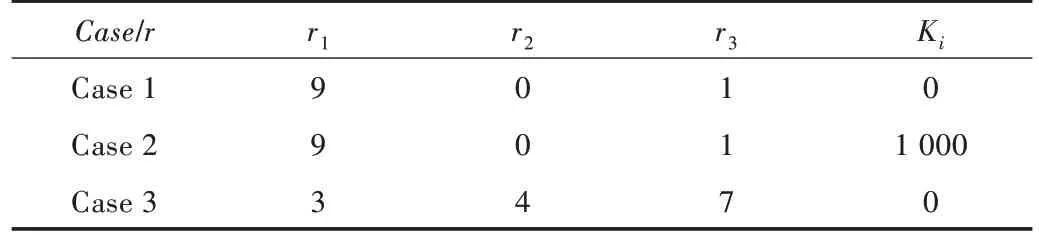
Table 2 Wolfram mathematica software modulates three sets of parameters表2 Wolfram mathematica 软件调制3 组参数

其中，第1 组导纳相角在稳定范围内，第3 组为特定不稳定条件。为降低系统的稳态误差，使20lg（输出/输入）趋近于0，因此考虑在其他参数不变的条件下增加一个积分环节Ki，同时也作为第1 组的对照组。

基于以上参数，根据Case1、Case2 中的参数分别进行仿真，得到图4、图5 中的波形。

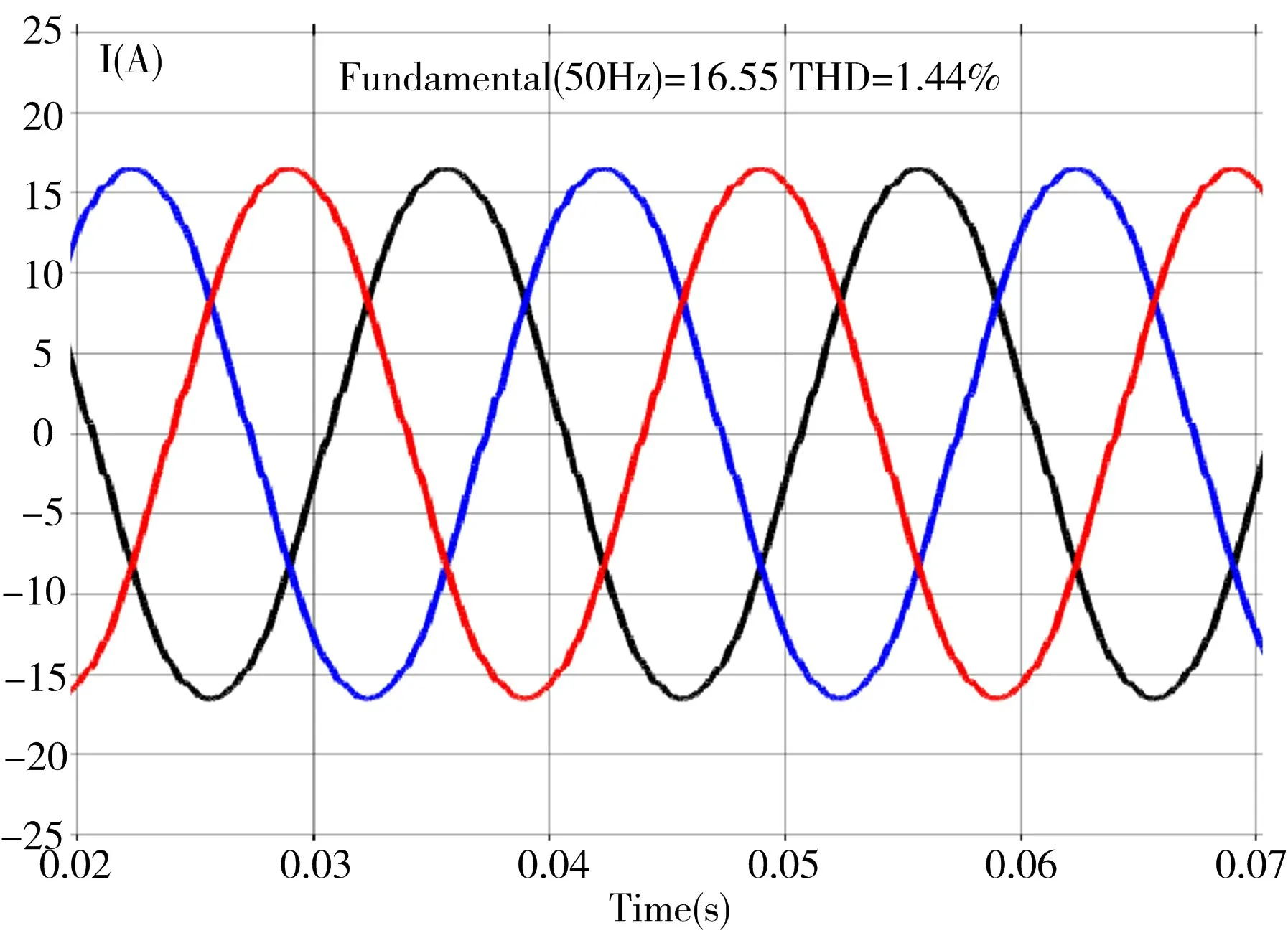
Fig.4 Simulation curve of Case1图4 Case 1 仿真曲线

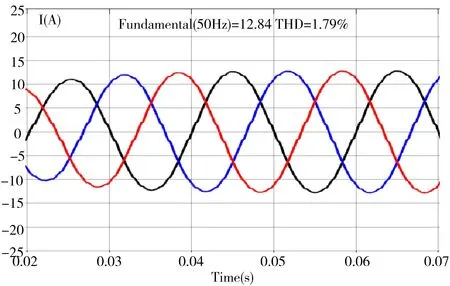
Fig.5 Simulation curve of Case 2图5 Case2 仿真曲线

从波形可以看出，经过滤波后，系统波形很平滑，谐波含量也均在合理范围内。然而，Case1 的稳态误差较大，而加入积分环节的Case2 输出则能够跟踪给定。从图6 可以看出，由于设置参数在系统稳定范围之外，得到的波形杂乱，因此可作为对照组。

Fig.6 Simulation curve of Case 3图6 Case3 仿真曲线

接下来继续验证系统的动态性能，当系统结构发生变化时，参数如表3 所示。

Table 3 System structure parameters表3 系统结构参数

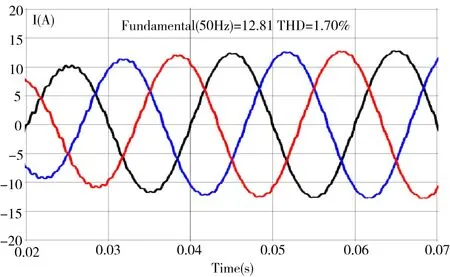
Fig.7 Structural parameter changes图7 结构参数变化

如图7 所示，虽然调低了逆变器侧电感，使得系统参数不平衡，但电流波形仍然能保持稳定且仅有轻微失真。此外，无论是增加还是减少50%额定功率，波形最终都能保持平滑稳定，而且谐波含量也在允许范围内，如图8 和图9所示。因此可以得出结论：在设计无源控制器参数时，可以设置其阻抗严格无源，以保证系统稳定，且能较好地适应系统参数与电网参数变化，而不需要利用Routh 判据或根轨迹法。

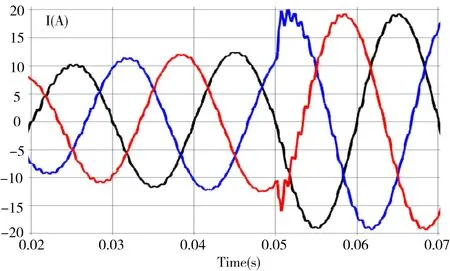
Fig.8 Increase rated power by 50%图8 增加50%额定功率

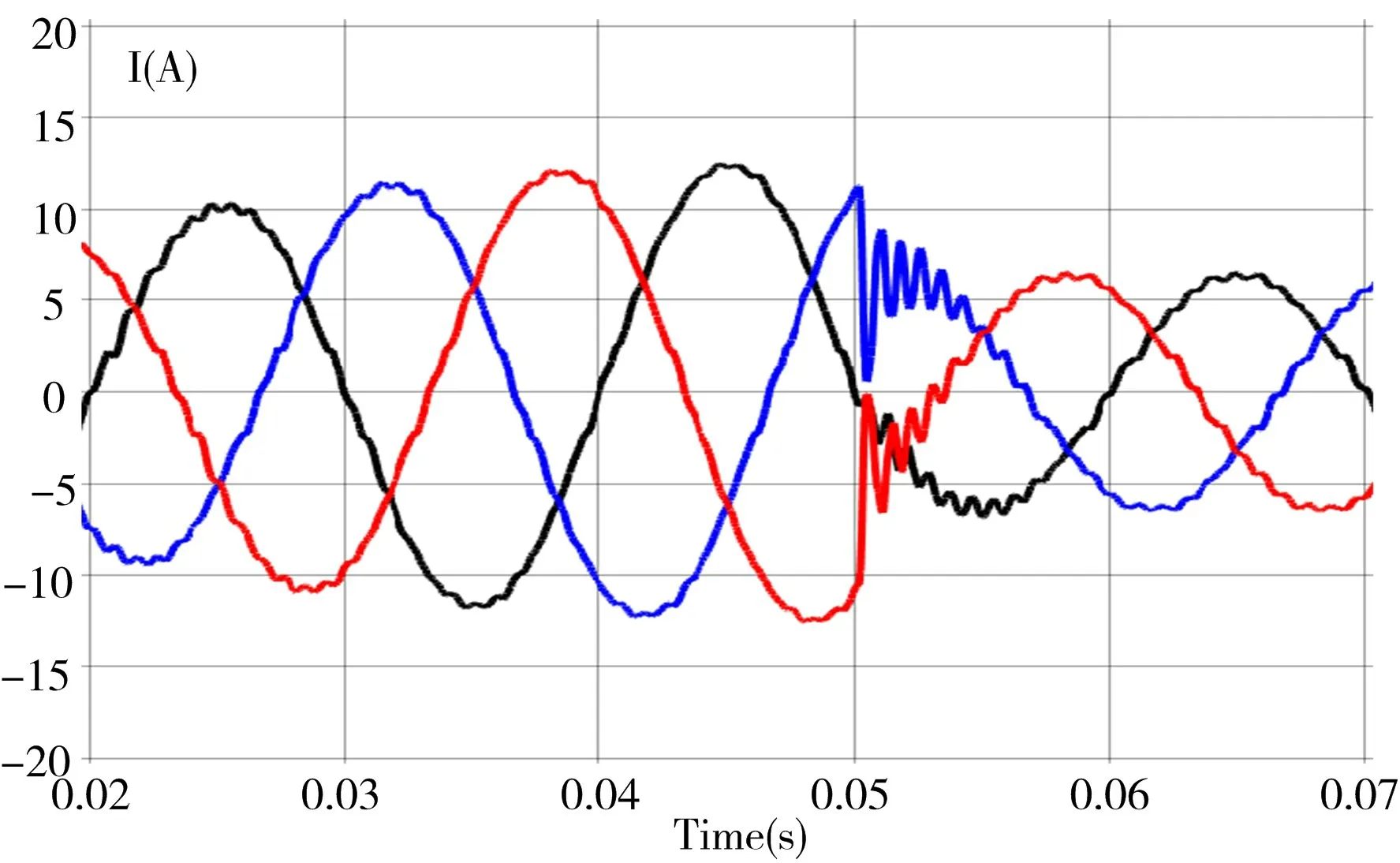
Fig.9 Reduce rated power by 50%图9 减少50%额定功率

5 结论

由于系统结构复杂且需要6 个状态变量，无源控制在LCL 型三相并网电压逆变器中的应用较少。本文首先在主回路拓扑结构上推理了系统E-L 数学模型；然后根据无源性理论，介绍一种只需要两个状态变量的无源控制器；最后经过仿真数据分析E-L 数学模型下的无源控制器波形，通过引入有源阻尼的思想，抑制LCL 滤波器自身存在的谐振尖峰。从仿真波形可以看出，在谐振频率处谐波依然能满足要求，且无论是额定功率在-50%～50%之间发生波动，还是结构参数L1、L2、C 发生变化，系统最终都能保持稳定。因此，相较于传统并网电流控制方法，无源控制策略表现出更好的稳定性与应对参数波动的鲁棒性。本文研究也存在不足：利用数学软件试凑的方法调制出满足设计要求的阻尼等参数，并没有对各个参数设计的理论依据展开讨论。