增量学习下的SVM-AdaBoost 信用评估方法

郭天添，高 尚

（江苏科技大学 计算机学院，江苏 镇江 212100）

0 引言

当代社会信用消费增长迅速，不仅仅是个人信用贷款，不少企业也需要进行贷款。因此，为了满足经济发展的需求，对于个人甚至是企业的消费能力、社会履约能力和信誉程度进行全面信用评估是必不可少的。信用评估的发展大致经历了3 个阶段，依次是专家分析、统计分析和人工智能［1］。一些机构和学者研究了行业竞争、管理、政策等因素，并将改进的统计学、人工智能等技术应用于信用评估以构建信用风险评估体系，并将历史经验与科学实证相结合，目前已逐渐研究出一系列信用评估方法和模型［2］。如今，科学的信用评估方法作为风险评估工具已被社会认可并得到广泛应用。

应用统计分析知识建立的信用评估模型非常多，最常见的包括判别分析（DA）、Logistic 回归（LR）以及分类树（CT）等，虽然利用这些模型进行信用评估成本低，也较为快速，但若是变量之间的线性关系不足，则模型的准确度不高。随着时代的进步和科技的发展，一些人工智能方法如决策树（DT）、支持向量机（SVM）、人工神经网络（ANNS）、贝叶斯分类器（BC）、模糊规则系统以及集成学习模型等［3-9］已被用来建立准确且稳定的信用风险评估系统［10］。例如文献［3］通过将分类树方法引入信用评估模型，利用分类树对申请信誉贷款的人进行分类。分类树方法充分利用先验信息处理申请人各项数据，从而有效对数据进行分类，可在最大程度上保证被分到同一类别的申请人都具有相似的违约风险，并尽量使每个类别的违约风险程度不同。这种处理方法结构非常简单，在处理一些数据量较大的样本时，具有较高的分类精确度和分类效率。文献［4］将神经网络方法引入信用评估模型中，神经网络依靠自身强大的学习能力，在训练样本中可自动学习知识。神经网络可以承载很多数据，面对这些数据能很快适应并作出相应处理。不仅如此，其在处理多分类问题时也有很高的准确率。但其需要较长的训练时间以及大量参数，可解释性差，模型复杂度较高时容易产生过学习现象。文献［5］使用K 近邻判别分析法（KNN）进行信用评估。KNN 具备轻松处理大数据和增量数据并避免参数过拟合的优点，但随着增量数据的不断引入，其会产生巨大的搜索空间，导致算法需要更长时间训练。

将深度学习算法［11］应用于信用评估模型可有效提高准确率，但深度学习算法复杂度较高，计算开销大，而在大数据应用场景下，多数评估指标在不断更新中，即使应用深度学习算法也无法即时重构合适的评估模型［12］。相比之下，机器学习中的经典算法SVM 和AdaBoost 算法具有算法简单、消耗资源少的优势。因此，本文在增量学习（Incre⁃mental Learning）模型框架下将SVM 与AdaBoost 相结合，构建一个总的IL-SVM-AB 分类器模型，并在南德信贷数据集上对其性能进行验证，以期获得更高的信用评估准确率及有效性。

1 相关理论

1.1 支持向量机

支持向量机（Support Vector Machine，SVM）是依据统计学习理论的VC 维理论和结构风险最小化原理发展而来的方法。SVM 算法思想不同于传统的最小二乘法思想，以二维数据为例，其具有两个特征：①需要尽可能地将两类样本分开；②两类样本点中所有离它最近的点都要尽可能远（见图1）。其中，A 线、B 线、C 线都将数据分成两类，但只有B 线才是最好的决策边界。该方法不仅可使结构风险最小化，并且在有限样本下具有很强的泛化能力。

在数据增多的情况下，在低维空间中可能就无法简单地将其直接分开。此时，SVM 通过核方法把数据对应到一个高维空间［13］，并通过一个超平面表示决策边界，最大化超平面与每个类别数据点之间的最近距离。在高维空间中看就如同是一个平面将这些数据完美分开，但在二维空间下可能就是一条不规则的曲线将数据分开。SVM 利用核方法有效提高了算法的泛化能力［14］，但在数据本身就是高维的情况下，SVM 处理起来则效果不佳，更加费时费力。

Fig.1 Principle of support vector machine图1 支持向量机原理

信用评估可被视为3 种问题，当被视为聚类问题时，人们需要处理的是，由未知类别对象的不同特征指标确定不同对象是否属于不同类别；当被视为分类问题时，人们需要处理的是，由不同类别的多个指标判断对象类别；当被视为回归问题时，人们需要处理的是，基于多个未知类别对象的多个指标估计多个对象的信用值。

基于SVM 的信用评估，其以训练误差作为优化问题的约束条件，以置信范围最小化作为优化目标，具有较好的推广能力。SVM 技术目前已经很成熟，不仅可用于分类问题，而且可以处理回归问题，因此非常适用于处理信用评估问题。另外，SVM 的优点还在于其解的唯一性，而且是全局最优解［15］。

1.2 AdaBoost（AB）

Boosting 是集成学习方法的一种，也被称为增强学习（提升法），可将一些预测精度略低的弱学习器增强为高精度的强学习器［16］。AdaBoost 是一种迭代算法，可应用于任意分类器，只要该分类器能够处理加权数据即可。

AdaBoost 分类器可排除掉关键训练集上不必要的数据特征，提升步骤通常分为3 步：首先通过训练集样本的权重训练弱分类器，然后根据其加权错误率重新分配权重，最后根据其表现更新权重。

AdaBoost 的自适应体现在增大之前分类器错误分类的样本权值，减小分类器正确分类的样本权值，以此类推。与此同时，不断在下一轮中加入一个弱分类器，一直达到期望的最小容错率或迭代次数达到最大，最终确定强分类器［17］。类似于人类学习新知识的过程，第一遍学习时会记住一部分知识，但往往也会犯一些错误，对于这些错误，人的印象会很深，在第二遍学习时就会针对相关知识加强学习，以减少类似错误的发生。不断循环往复，直到犯错误的次数减少到很低的程度。

1.3 增量学习

增量学习［18-19］是一种机器学习方法，其输入的数据被不断用于扩展现有模型知识，即进一步训练模型。该方法是一种监督学习和非监督学习的动态技术，当训练数据逐渐增加或数据大小超出系统内存限制时，可应用该方法对持续增加的数据进行监控与切片，并对切片后的部分数据进行训练，直到训练完所有数据。学习率控制新数据的适应速率，然而对新知识的学习必然导致对旧知识的遗忘。可设置永不遗忘其所学习的知识，应用此类设置的算法被称为稳定的增量机器学习算法。

传统分类算法面对样本数量的不断增加或评价指标的不断更新，数据样本的特征属性也会不断更新，从而面临维数灾难问题［20］。增量学习是对新增样本集不断更新学习的方法，其思想充分考虑到新增样本集对原有样本集的影响，同时又充分利用历史分类的结果，使学习过程具有延续性。增量学习算法不需要过多的内存空间保存历史数据，而且在对新增样本进行训练时，利用历史训练结果进行运算，可明显缩短训练时间，提高训练效率。增量学习算法适用于对大量数据集进行挖掘，并且在新增训练数据不断被引入的情况下，可得到更高效的训练结果。

2 LS-SVM-AB 分类器设计

文献［6］将SVM 引入到信用评估中，最大程度地降低了结构风险，并确保在有限样本甚至小样本情况下，依旧具有强大的泛化能力；文献［7］利用AdaBoost 方法对个人信用进行评估，由于AdaBoost 方法是由多个基分类器组合而成的，可极大程度上提升弱分类器的准确率和使用率，使各个分类器都各司其职。

在现实生活中，信用评估并不容易，一些金融机构会尽可能收集与积累大量数据，总结出具有“好”和“不好”信用的客户规律，以减少机构面临的风险，但这些数据中的所有特征属性并不都是必需的，从而造成了数据冗余和灾难。过多的无用属性会在无形中增加模型计算复杂度，还会降低模型工作效率。然而，单个SVM 模型不能主动进行特征选择及降维，但是AdaBoost 方法可以极大程度上解决该问题。在此基础上，本文提出在增量学习框架下设计的IL-SVM-AB 信用评估模型。当引入数据时，先大致判断是否直接可分，以及数据样本量是否超过设定值。如果直接可分并且是小样本情况下，直接使用SVM 处理数据；若不满足以上情况，转入SVM-AdaBoost 处理系统，即使用多个加权SVM 对数据进行处理。其包含3 个子系统：一是增量学习框架，二是数据判断系统，三是SVM-AdaBoost 数据处理系统。

2.1 参数优化

支持向量机的性能是由其参数以及核函数决定的。在本次设计的IL-SVM-AB 模型中，通过网格搜索确定最优核函数为高斯径向基核函数，惩罚参数C 为1 时模型训练效果最佳。惩罚参数C 的作用相当于是对模型分类准确度及分类间隔大小的权衡。当C 取值越大，表示其对模型分类准确度要求越高，也即要杜绝分类错误的样本，因而容易产生过拟合；当C 取值越小，表示模型只重视分类间隔是否足够大，而不在乎分类准确率，模型容易出现欠拟合现象。核函数的改变实际上是改变了样本空间的复杂程度，使用不同核函数会变换到不同的特征空间。为了防止模型过拟合或欠拟合，惩罚参数C 和核函数参数选择一定要在训练模型上反复斟酌，通过实践得出最合适的参数。本文通过网格搜索与交叉验证方法确定IL-SVM-AB 信用评估模型基分类器的参数，以此保证分类器的状态。

2.2 模型建立

增量学习框架如图2 所示。

Fig.2 Incremental learning framework图2 增量学习框架

模型对数据处理的第一步是判断数据是否需要系统进行处理，通过生成决策树判断数据是否为高维数据，即是否可以快速、准确地分为两个类别，并判断数据样本量是否在阈值内。若能达到以上两种设定情况的要求，则通过将数据直接传递给SVM 算法作下一步处理；若待分类样本不属于同一类别，或数据样本量超出阈值，则通过SVMAdaboost 模型处理数据。数据判断系统如图3 所示，SVMAdaBoost 数据处理系统如图4 所示。

Fig.3 Data judgment system图3 数据判断系统

Fig.4 SVM-AdaBoost data processing system图4 SVM-AdaBoost 数据处理系统

IL-SVM-AB 信用评估模型具体步骤如下：

步骤1：数据预处理。查看数据分布情况，如图5 为每个数据特征直方图，X 轴表示每个特征取值区间，Y 轴表示满足该特征区间的样本数量。

将数据通过Box-Cox 转换为正态分布，具体情况如图6所示，可在一定程度上减少无法观察到的误差。相对于直方图，转换之后的数据特征在显示时会更加平滑，也可用来预测变量的相关性。

图7 显示的是数据特征的两两相关性，坐标轴显示的是每个数据特征。通过这种类型的特征关系图，可看到数据之间的关联，大致判断哪些特征对分类情况没有影响，实际操作时可尝试将这些毫不相关的特征pass 掉。

步骤2：确定初始训练集与测试集。分离出评估数据集是一个非常好的办法，因为是在同一数据集下进行分离的，不仅可确保两组数据集的数据特征量相同，而且可以保证评估数据集和用于模型训练的数据集互不影响，最后还可利用该评估数据集分析与判断模型的准确度。本次实验分离了30%的数据作为测试集，70%的数据作为训练集。

步骤3：数据选择。根据步骤2 得到的数据集，若数据特征维数在设定值之下，则开始训练SVM 分类器；若数据特征维数过高，则构建SVM-AdaBoost 分类模型。假设数据集中总共有N 条数据，将这N 条数据平均分成K 份子集，每个子集中则有N/K 条数据。在每次验证时，用已划分好的K 个子集中的一个作为测试集，然后将剩下的子集用于训练集训练，之后用测试集进行模型评价。在SVM 分类器训练方面，对训练数据集采用网格搜索法确定SVM 参数。基于此次训练结果，惩罚参数C 为1，当径向基函数kernel为RBF 高斯径向基核函数时训练效果最佳。

步骤4：SVM-AdaBoost 模型构建。实际中以银行为例，拒绝信用“好”的客户和接受信用“坏”的客户两种错误造成的损失并不相同。拒绝信用“好”的客户，可能损失的只是如贷款利息一些影响不大的利润。但若接受信用“坏”的客户，银行则可能遭受巨大的违约风险，并涉及到法律问题。也即是说，接受具有“坏”信用客户的成本比拒绝具有“好”信用客户的成本高得多，得不偿失。为了提高模型的实用性，设置损失比例似乎是一个不错的选择。

Fig.5 Histogram of data features图5 数据特征直方图

Fig.6 Normal distribution transformation of data图6 数据正态分布转换图

在模型训练过程中，通过损失比例对训练集数据特征进行加权，根据每个特征在信用评估中的重要性进行权值初始化，每个特征对应一个SVM 分类器，即对每个SVM 分类器进行加权处理；在AdaBoost 提升框架中加入加权SVM，通过提升框架，初始训练集会得出多样化的训练集子集，然后通过该子集生成基分类器，从而计算SVM 分类的错误率。基分类器由多个SVM 特征组成，因此在给定K 轮训练数后即可生成相应的基分类器。每个基分类器的识别率虽然不是很高，但是联合后的分类器具有很高的辨识率，从而提高了算法识别率。对提升后的分类器进行加权，生成最终的结果分类器。SVM-AdaBoost 模型是由多个弱分类器加权构成的强分类器模型，而SVM 是一个强分类器，现在作为一个弱分类器加入到AdaBoost 模型中，效果也是显而易见的。

Fig.7 Data characteristic correlation diagram图7 数据特征相关图

步骤5：此时的数据集是分类器最原始的知识库，将增量数据作为新学习的知识加入已存在的知识库中。依旧对特征值进行权值评定，若特征是新加入进来的，有多少个特征则追加相应数量的SVM 分类器，但需要在SVM-Ad⁃aBoost 数据模型中找到每个数据合适的位置，插入增量数据。SVM 算法部分根据得到的新数据集，依据步骤4 训练模型。

步骤6：根据评价指标，将本文基于增量学习的SVMAB 信用评估模型与其他信用评估模型进行对比。

3 实验及结果分析

3.1 实验数据

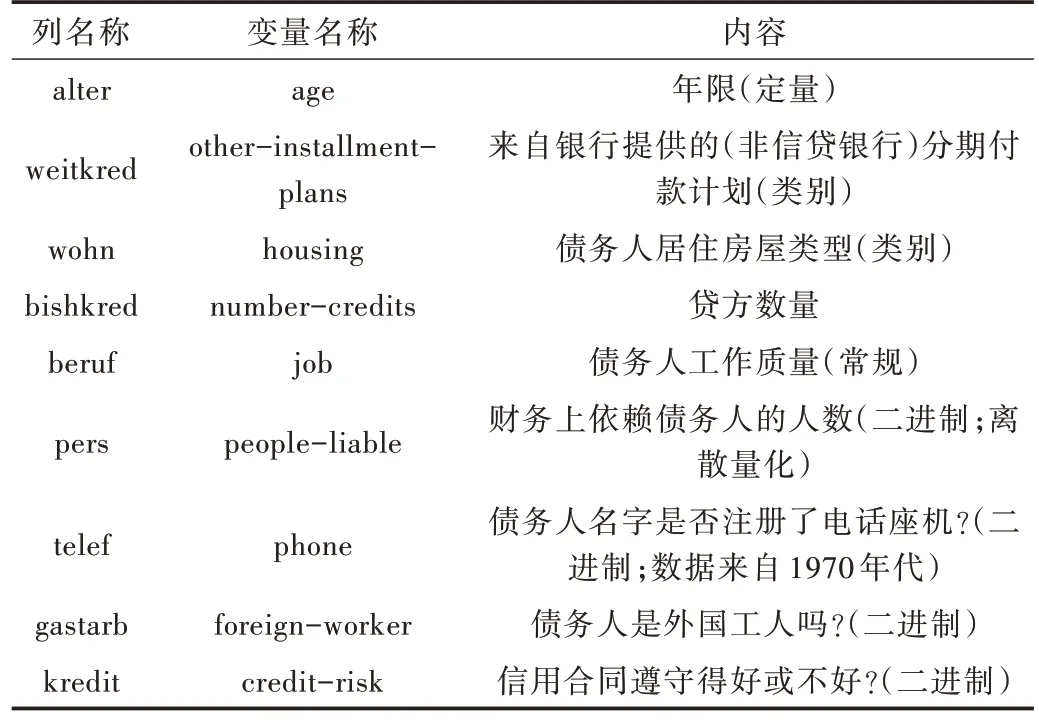
本文实验采用UCI 上的南德信贷2020 版数据集（https：//archive.ics.uci.edu/ml/machine-learning-databases/00573/），数据集包括700 条信用好和300 条信用不好的客户数据，如表1 所示，每条数据包含21 种数据变量。若信誉好，则变量kredit 中的标记为1，若信誉不好，则标记为0。

Table 1 Property description of South Germany credit data set表1 南德信贷数据集属性描述

3.2 评价指标

最常见的评价指标是模型的准确率A、精确率P、召回率R 以及F1 值，都可通过混淆矩阵计算得到。

准确率A 表示正确分类信用“好”的客户以及信用“坏”的客户数量在所有分类客户中的比例，取值范围为0～1，值越高表示越准确。

精确率P 表示正确分类信用“坏”的客户数量在预测为信用“坏”客户中的比例，取值范围为0～1。

召回率R 表示正确分类信用“坏”的客户数量在实际为信用“坏”客户中的比例，取值范围为0～1。

通过计算精确率P 和召回率R，得到其调和均值，即F1值，取值范围为0～1，0 最差，1 最好。

最后取准确率A 和F1 值作为评价指标评估模型优劣。信用评估旨在挑选出信用“坏”的客户，因为若信用“坏”的客户被判断成信用“好”的客户，其承担的风险更高，所以混淆矩阵定义如表2 所示。

Table 2 Definition of confusion matrix表2 混淆矩阵定义

各项评价指标计算方法如下：

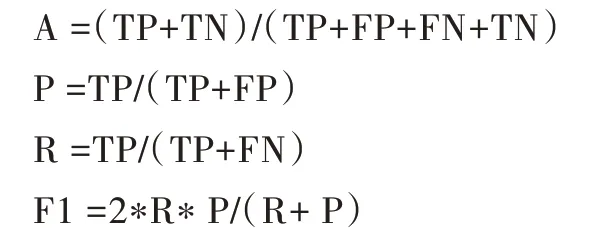
3.3 实验结果

表3 给出了使用各传统算法构建信用评估模型之后在南德信贷数据集上的实验结果，表4 给出了使用各集成算法构建信用评估模型之后在南德信贷数据集上的实验结果，图8 给出了总的模型实验结果对比。从实验结果可以看出：①在每次实验中，根据常用的评价指标来看，本文模型的效果都是最佳的，证明了该方法用于信用评估是有效的；②集成模型相比传统模型的分类准确率普遍更加稳定，准确率偏差不太明显；③将此次设计的IL-SVM-AB 模型用于信用评估分类，比直接用SVM 分类时的F1 值提高了17.5%，准确率A 提高了9.7%；在相同情况下，比直接用AdaBoost 分类时的F1 值提高了17.6%，准确率A 提高了11.7%。可以明显看到，在增量学习框架下，AdaBoost 与SVM 可以很大程度上实现互补。

Table 3 Comparison of traditional models表3 传统模型比较

Table 4 Comparison of integration models表4 集成模型比较

Fig.8 Comparison of experimental results图8 实验结果对比

4 结论与展望

本文在SVM 与AdaBoost 算法基础上融合增量学习思想，提出适用于信用评估的IL-SVM-AB 算法。实验结果表明，该算法模型的准确率不仅优于传统线性算法LR 以及非线性算法KNN、NB、SVM 和CART 等，而且优于RF、ET、Ad⁃aBoost、GBM 等集成算法。本文设计的IL-SVM-AB 模型不仅对SVM 与AdaBoost 进行了参数优化，而且将加权SVM 加入到AdaBoost 提升框架中进行数据特征筛选，形成新的分类器进行分类，并在增量学习框架下进行分析与评估。该方式不仅保证了新模型在大数据时代下不会因新增数据的加入，导致准确率下降或时效性不足而被淘汰，而且能利用这些新增数据或指标更好地完善模型。此次选取的数据集相当于二分类问题（信用好或不好），因此未来进一步研究方向如下：①如何在保证准确度的前提下（提高准确度更佳）将模型应用于多分类问题；②在增量学习框架下，在其中加入两个甚至更多分类器组合模型，例如随机森林、神经网络及随机梯度上升算法等，使模型效果更优；③如何选取新模型进行属性约简，在增量学习框架下更好地进行新增数据筛选；④在大数据时代，数据挖掘也是一个不错的方向。