内孔结构对旋转空化发生器水力特性的影响

谢 超， 张 伟， 孙伟华， 谭 磊

清华大学 能源与动力工程系 水沙科学与水利水电工程国家重点实验室， 北京 100084

0 引 言

空化是一种包含汽液相间质量传输的非定常、可压缩、多相湍流的复杂流动现象[1-3].空化流态伴随着空泡的产生、发展和溃灭，以及两相间质量和能量传输，可实现化学反应加速、污水处理、有机物分解、萃取提纯、微重力作用等工程应用[4-5]，具有广阔的应用前景.通过空化发生器诱发空化并将其应用于工程是近年来的研究热点.

按照基本结构的不同，水力空化发生器一般可以分为孔板式[6]、文丘里管式[7]和旋转式[8].孔板式和文丘里管式空化发生器的研究起步较早，但由于这两类空化发生器通过截面积变化诱发空化，空化量产生受到限制.而旋转式空化发生器利用离心力产生空化，结构简单，流量大.PETKOVSEK等[9]通过改变温度、过氧化氢含量和空化时间，研究了旋转结构空化器污水处理的能力；KIM等[10]开展了旋转式空化发生器处理污泥的实验，结果表明其颗粒分解和氧化性能都优于超声波空化；MILLY等[11]采用旋转式空化发生器对流食进行杀菌，结果发现其诱发的微生物致死率大于热效应；BADVE等[12]采用旋转式空化发生器对工业废水进行处理，研究得到了转子转速、过氧化氢试剂浓度和处理时间的最优值.刘影等[13]基于FBM湍流模型和Kubota空化模型，分析了旋转式空化发生器的孔倾角、孔径和孔深等结构参数对空化的影响；BADVE等[14]通过数值模拟分析了空化器旋转过程中流线结构、压力场和剪切速率的变化规律；袁惠新等[15]基于Realizablek-ε湍流模型和Zwart-Gerber-Belamri空化模型对旋转齿筒水力空化器进行数值模拟，结果发现空化器主要受离心力和剪切力影响.

本文采用高速相机摄影和数值模拟方法研究旋转空化发生器内部空化流态和压力脉动特性，并分析不同内孔结构对其影响，为旋转水力空化发生器的优化设计奠定基础.

1 数值模拟

1.1 旋转空化发生器几何参数

旋转空化发生器主要由转子和腔体组成，转子上沿圆周方向均匀分布24排内孔，沿轴向均匀分布5排内孔，转子直径为264 mm.旋转空化发生器如图1所示.转子在电机的驱动下旋转并在内孔形成空化，转速为1 200 r/min.

图1 空化器实物图Fig.1 Physical picture of cavitation generator

图2(a)为转子截面示意图，图2(b)为圆锥形内孔，图2(c)为圆柱形内孔，图2(d)为椭圆形内孔，3种内孔的深度均为55 mm.

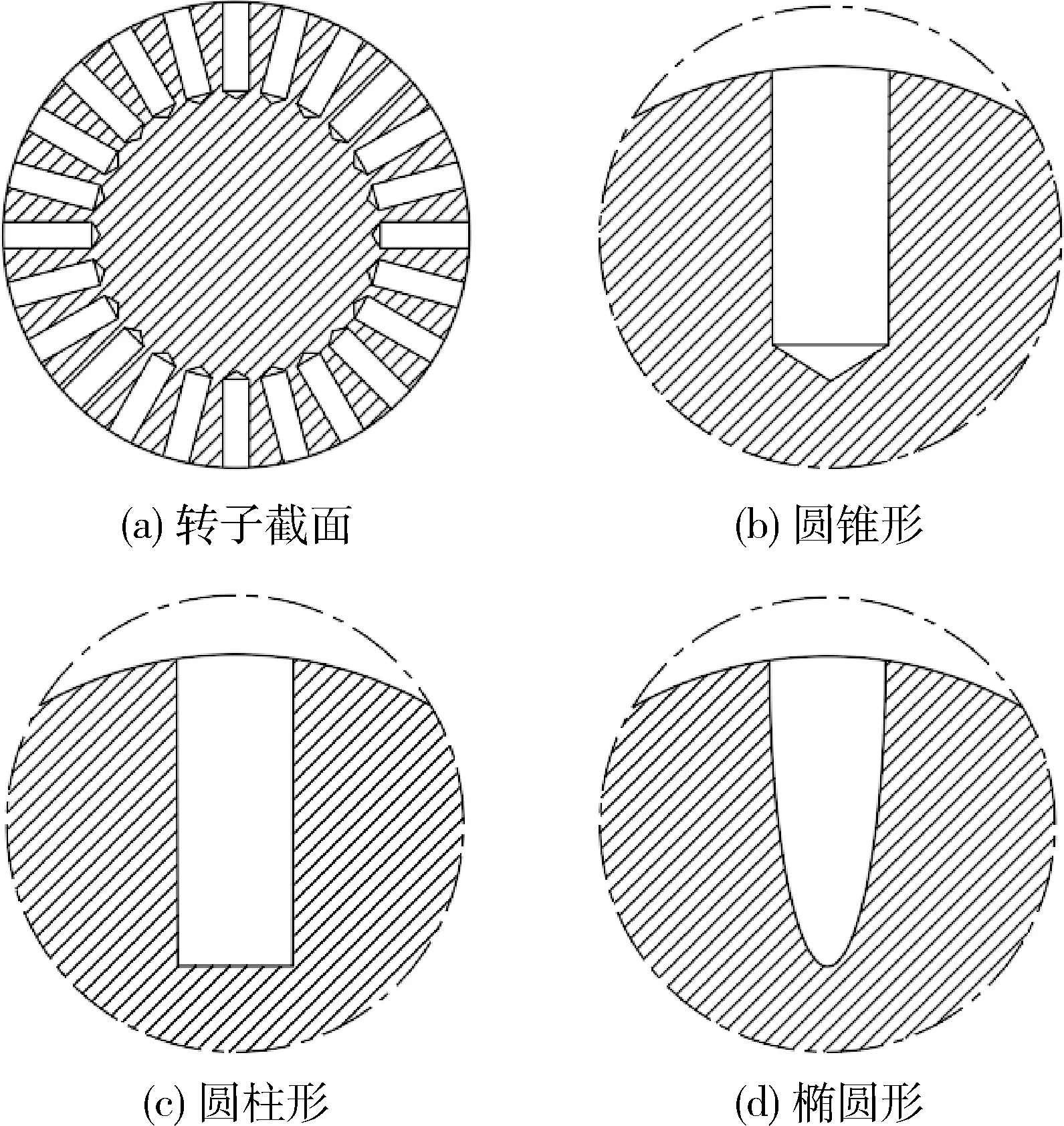
图2 转子截面及内孔结构Fig.2 Rotor section and inner hole structure

采用ANSYS ICEM18.0软件进行网格划分，将流体域模型分为4个部分：入口域、腔体域、转子域和出口域.其中入口域，腔体域和出口域采用结构化网格，转子域采用非结构化网格，近壁面网格进行局部加密处理，总体网格如图3所示.

图3 计算域及网格Fig.3 Computing domains and grids

对旋转空化器进行网格无关性验证，选择4组不同密度网格，如表1所示，当转子域网格数由1 534 080增长为1 930 000时，计算所得进出口压差变化较小，考虑计算资源、时间成本，本文采用全流道计算域网格单元数为4 018 800.

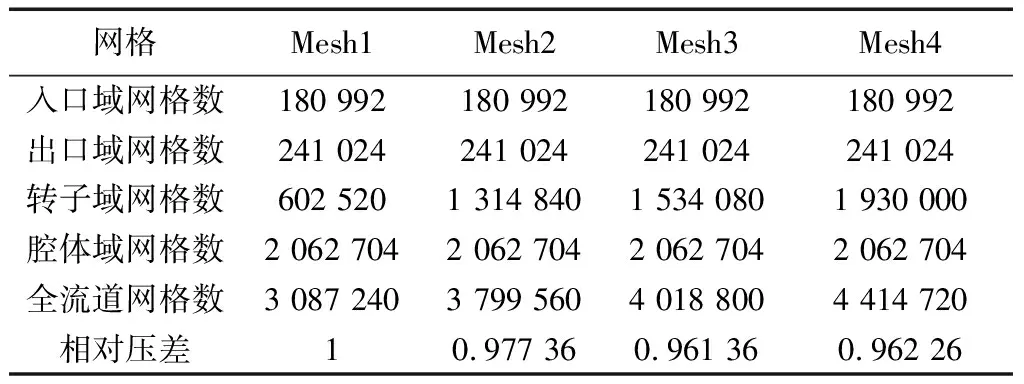
表1 网格无关性验证Tab.1 Grid independence validation

1.2 基本控制方程

流体运动基本控制方程为基于Reynolds平均的Navier-Stokes方程.

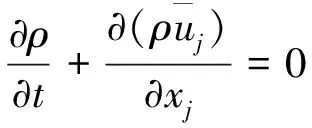
(1)

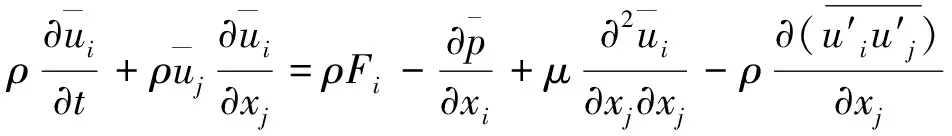
(2)

式中，ρ为密度，t为时间，u为速度，μ为粘性系数，F为体积力.采用适合水力机械强旋转流和带弯曲壁面流的RNGk-ε[16]双方程湍流模型封闭控制方程组.

1.3 空化模型

采用Zwart-Gerber-Belamri空化模型求解汽相体积分数：

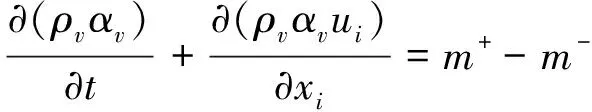
(3)

(5)

式中：m+，m-分别表示质量蒸发速率和质量凝结速率；αv为空泡体积分数；ρv为汽体密度，其值为0.023 08 kg/m3；ρl为液体密度，其值为997 kg/m3；pv为液体饱和蒸气压力，其值为3 574 Pa;Cvap，Ccond为蒸发相经验系数和凝结相经验系数，取值分别为50和0.01[17].

1.4 计算方法

基于CFX20.0对旋转空化器内部流动进行数值模拟，计算工况与试验保持一致.定常计算中，设置转子转速为1 200 r/min，进口总压为90 000 Pa，出口质量流量设置为2.5 kg/s，温度为室温25℃，固体壁面设置为不可滑移边界.非定常计算中，以定常计算的结果作为初始值.

空化器旋转一周的时间记为T，非定常计算中为验证时间无关性，时间步长Δt分别取值为相邻两个内孔转过同一位置的时间间隔的1/16，1/32和1/64，对应T/24/16=0.000 130 2 s，T/24/32=0.000 065 1 s，T/24/64=0.000 032 6 s，每个时间步长内迭代1～20次，在内孔中布置5个监测点，沿内径到外径方向依次设为V1、V2、V3、V4和V5，3个时间步长的计算结果如图5所示，结果差别很小，考虑计算成本，本文取Δt=0.000 130 2 s.

图4 时间步长无关性验证Fig.4 Time step independence verification

2 数值模拟结果及分析

2.1 内孔流动分析

图5为旋转空化发生器内孔的压力和流线分布图，由图可知孔内的压力从内径到外径逐渐增大，这是因为转子旋转产生离心力推动流体朝外径方向运动，在腔体的限制下被局限在内孔出口处，导致压力增大.孔内流体在转子旋转作用下形成大尺度的漩涡Ⅰ和小尺度漩涡Ⅱ.漩涡Ⅰ位于内孔底部，主要是惯性力引起的轴向漩涡而产生的，流体在该区域耗散能量.漩涡Ⅱ位于内孔顶部，主要是腔体区主流撞击在内孔侧壁，部分流体进入和流出内孔，形成漩涡.

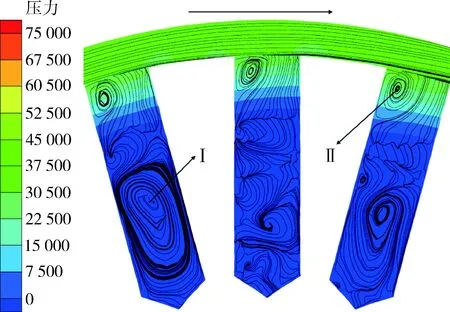
图5 流线及压力云图Fig.5 Streamline and pressure nephogram

图6所示为内孔流动状态的高速相机拍摄结果，当孔内压力较大时，孔内无空化现象，如图6(a)所示.随着空化发生器进口压力降低，孔内压力随着降低，孔内开始出现空化，如图6(b)所示.

图6 孔内高速相机拍摄结果Fig.6 The results captured by a high-speed camera inside the hole

在与试验工况相同条件下开展空化发生器空化流动数值模拟，图7所示为孔内空化的数值模拟结果，结果表明数值模拟得到的空化区域与试验结果吻合较好，验证了数值模拟方法的准确性.

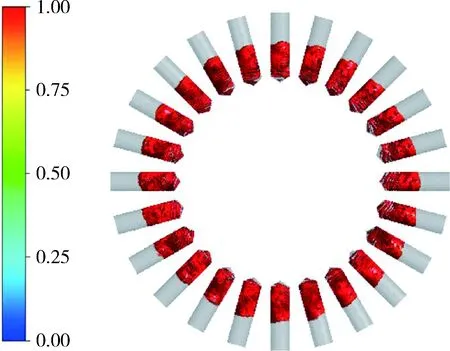
图7 孔内空化数值模拟结果Fig.7 Numerical simulation results of cavitation in hole

2.2 内孔结构对空化的影响

图8为相同工况下不同内孔结构内部的汽相云图.结果表明椭圆形内孔的空化区域最小，圆柱形内孔的空化区域最大.圆锥形、椭圆形和圆柱形内孔的汽相体积占比分别为68%，23%和80%.说明圆柱形内孔的空化发生效果最好.

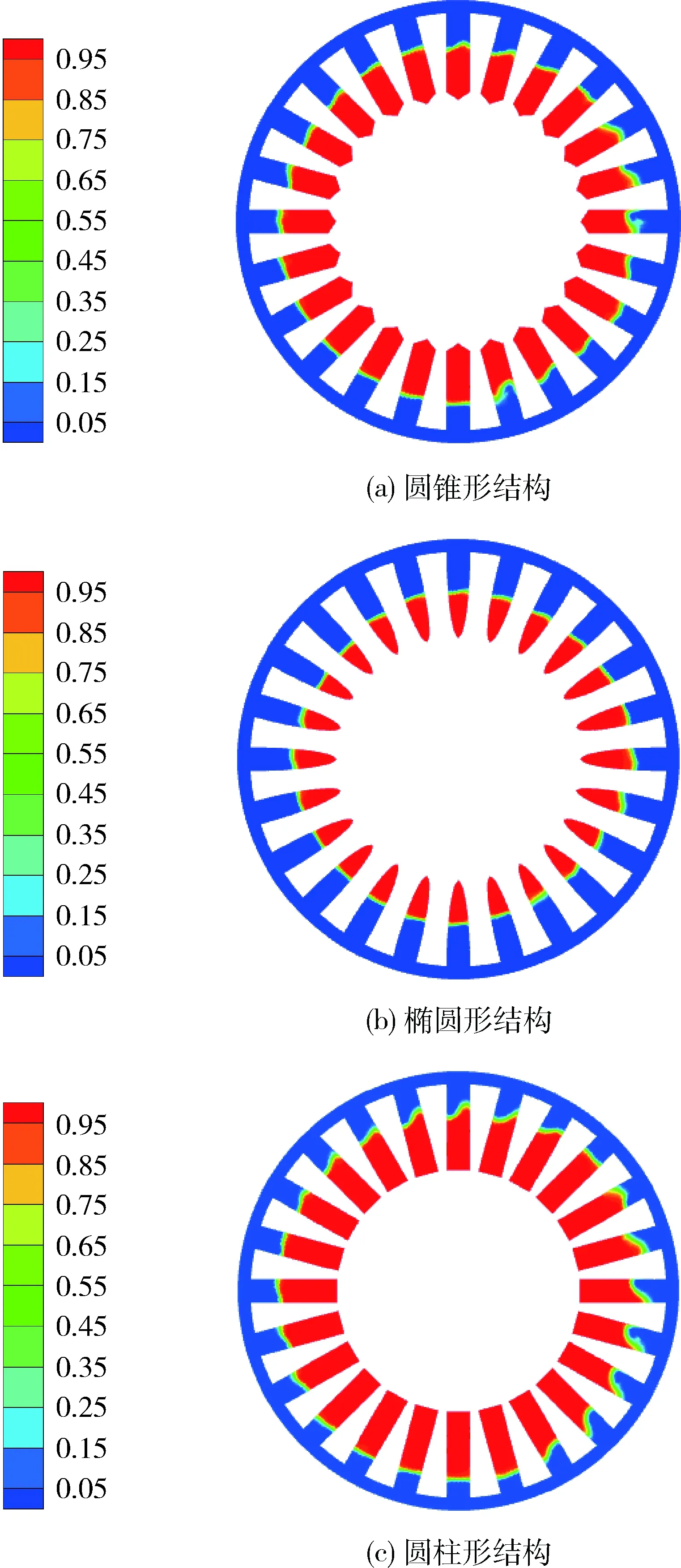
图8 不同内孔结构的汽相分布Fig.8 Vapor phase distributions of different internal pore structures

图9为相同工况下不同内孔结构内部的压力云图.低压区与汽相区基本一致，椭圆形内孔的压力整体上高于圆锥形和圆柱形.这是因为椭圆形内孔的型线较为光滑，局部损失小.综上所述，不同内孔结构对孔内流场和空化产生影响，型线光滑的内孔结构产生的空化较弱，该结论为后续旋转水力空化发生器的优化设计提供了参考.

2.3 压力脉动监测点

为分析不同内孔结构对空化发生器压力脉动的影响，在空化发生器腔体上布置监测点，在靠近进口处沿流动方向依次设为P1、P2、P3、P4和P5，在靠近出口处沿流动方向依次设为P6、P7、P8、P9和P10，如图10所示.

图9 不同内孔结构的压力分布Fig.9 Pressure distributions of different internal pore structures

图10 压力脉动监测点Fig.10 Pressure pulsation monitoring point

2.4 压力脉动频谱分析

非定常计算的总时间为12个转子旋转周期，取第6到第12个周期的压力脉动数据进行快速傅里叶变换(FFT)，得到压力脉动的频谱特性.由转子转速1 200转/分可知转子转频fi=20 Hz.

图11为靠近入口处5个监测点的压力脉动频谱特性.圆锥形内孔空化器P2的压力脉动主频为fi，振幅从大到小对应的频率为fi，24fi，72fi和48fi.椭圆形和圆柱形内孔P2的压力脉动主频为24fi，振幅从大到小对应的频率为24fi，fi，72fi和48fi.距离入口处最近的监测点P1压力脉动主频为24fi，振幅从大到小对应的频率为24fi，fi，72fi和48fi；P3、P4和P5的压力脉动主频为fi，振幅从大到小对应的频率为fi，24fi，72fi和48fi.

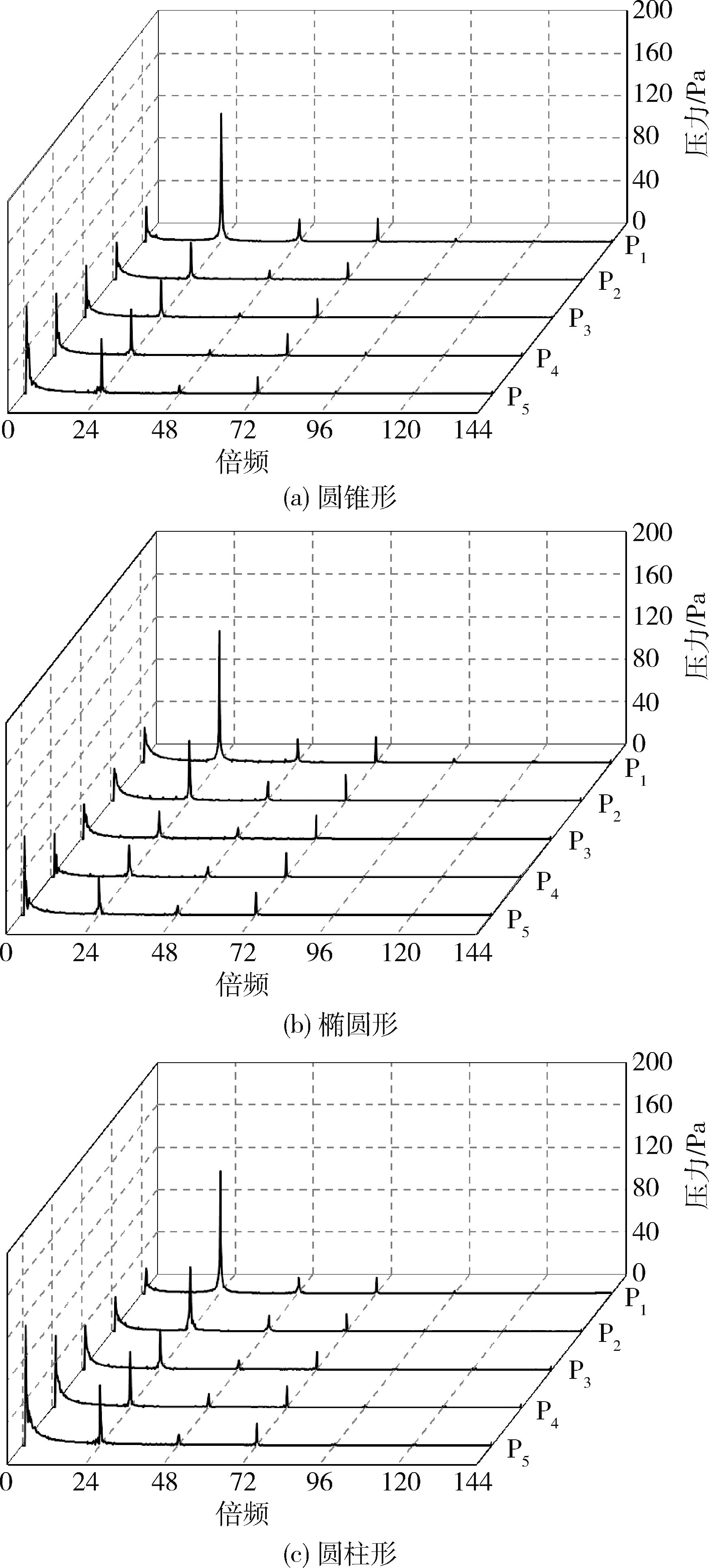
图11 不同内孔结构P1～P5压力脉动频谱Fig.11 Pressure pulsation spectrum of P1-P5 with different inner pore structures

图12为靠近出口处5个监测点压力脉动的频域特性.3种结构空化器P6～P10监测点的压力脉动主频均为24fi，距离出口处较远的3个监测点P6、P7和P8的次频为fi，振幅从大到小对应的频率为24fi，fi，72fi和48fi.距离出口处较近的两个监测点P9和P10的次频为72fi，振幅从大到小对应的频率为24fi，72fi，fi和48fi.

表2为3种内孔结构下，空化发生器各监测点上24倍转频对应的压力脉动幅值.结果表明，3种内孔结构下P1～P5五点处的压力脉动最大幅值均位于P1点，圆锥形、椭圆形和圆柱形的值分别为121.2 Pa、124.0 Pa和115.4 Pa.3种内孔结构下压力脉动最小幅值均位于P3点，圆锥形、椭圆形和圆柱形的值分别为35.6 Pa、26.0 Pa和37.6 Pa.沿P1-P5方向，压力脉动幅值呈现先减小后增大的趋势.对P6-P10而言，压力脉动最大幅值位于出口.圆锥形和椭圆形的压力脉动最大幅值位于P10处，其值分别为112.2 Pa和96.3 Pa，圆柱形的压力脉动最大幅值位于P9处，其值为129.6 Pa.综上所述，3种不同内孔结构空化发生器内部压力脉动最大幅值位于进口侧和出口侧，说明由于转子与进出口管之间相对运动而形成的动静干涉作用是压力脉动的主导因素.

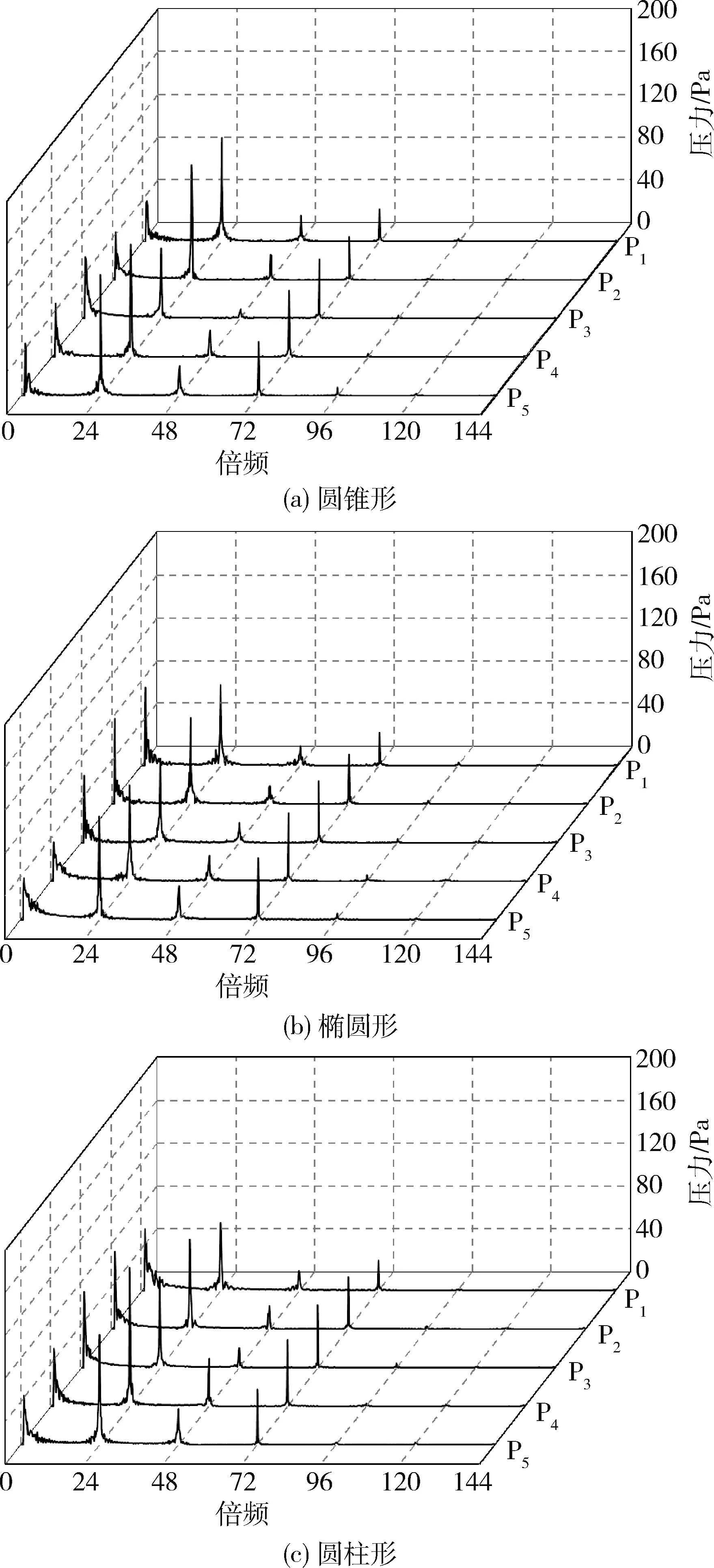
图12 不同内孔结构P6～P10压力脉动频谱Fig.12 Pressure pulsation spectrum of P6-P10 with different inner pore structures

表2 空化发生器内压力脉动幅值(24倍频)Tab.2 Amplitudes of pressure pulsation in cavitation generator(24 fi)

3 结 论

本文采用高速相机摄影和数值模拟方法，研究了三种内孔结构下旋转空化发生器内部空化流态和压力脉动特性，主要结论如下：

(1)数值模拟所得空化区域与高速相机试验观测结果吻合较好，验证了本文数值模拟方法的准确性和可靠性.

(2)内孔底部流体受惯性力引起的轴向漩涡的作用，产生较大漩涡；内孔顶部流体与腔体区主流相互作用，产生回流和较小漩涡.

(3)相同工况下，椭圆形内孔的空化率小于圆锥形和圆柱形，说明内孔结构对旋转空化发生器的空化效果产生重要作用，型线光滑的内孔结构产生的空化较弱.

(4)三种不同内孔结构下，旋转空化发生器内部压力脉动的主频为转频fi或24fi(对应圆周方向开孔排数).三种不同内孔结构下，旋转空化发生器内部压力脉动最大幅值出现在进口管侧和出口管侧，说明动静干涉是压力脉动的主导因素.