改进直觉模糊熵和证据推理的多属性群决策方法
2021-08-02高一凌龚本刚张孝琪
高一凌,龚本刚,张孝琪
(安徽工程大学 经济与管理学院,安徽 芜湖 241000)
由于决策问题的复杂性和决策环境的不确定性等原因,决策者在实际决策过程中往往难以获取精确的评估参数。为了更好地刻画决策信息的模糊性,Zadeh于1965年提出模糊集理论,之后Atanassov引入非隶属度将其进一步完善,建立了直觉模糊集(Intuitionistic Fuzzy Sets)。直觉模糊集拓展了模糊集中“非此非彼”的思想,为决策者提供了更丰富的手段来描述不确定性评价信息。因而,自提出以来在管理决策领域得到快速发展和应用,相关研究集中在集结算子、得分函数、不确定性测度、相似度度量和直觉模糊熵等方面。
直觉模糊集理论通过隶属度和非隶属度以及犹豫度来灵活地刻画评估信息。然而,在实际决策过程中,该理论在引入新参数的同时,也给决策矩阵和数据收集增加了不确定性。在模糊集中,熵可以作为不确定性的一种度量方式。由此,直觉模糊集的熵引起了相关学者的关注,在Burillo提出最初的直觉模糊熵和Szmidt给出其公理化定义后,直觉模糊熵及其公理化定义不断地得到拓展。如Verma在Atanassov直觉模糊集理论基础上提出了一种指数直觉模糊熵测度;赵飞认为直觉模糊集的不确定性由未知信息的直觉不确定性和已知信息的模糊不确定性共同构成,并且直觉模糊熵应是唯一的,由此提出一种直觉模糊熵的公理化定义并构造了新的度量方法;高明美从直觉模糊集的隶属度与非隶属度之间的距离以及犹豫度对直觉模糊熵的贡献角度出发,改进公理化定义并构造新的直觉模糊熵的计算公式。
在考虑直觉模糊多属性决策的情形下,Yuan给出一类新直觉模糊熵并将其与几种传统直觉模糊熵定义的权重结果进行了仿真分析,结果表明权重不仅依赖于熵的定义,而且依赖于备选方案和属性的个数;陈业华提出一类改进的直觉模糊熵并将其应用于应急决策中;王坚强将直觉模糊熵运用到直觉语言集中去,构建最优权重模型,并通过直觉语言加权算术平均算子实现对评价信息的集结;江文奇针对准则值为区间直觉模糊数且准则权重为区间数的多准则决策问题,提出基于二元联系数的区间直觉模糊型多准则决策方法。
证据推理方法是对D-S(Dempster-Shafer)证据理论的发展,它在处理不确定性、模糊性的多属性决策问题中具有明显优势,并得到广泛应用。该方法通过正交和运算将多源评价信息进行集结得到结果。代文锋将Burillo提出的直觉模糊熵和证据推理方法相结合,提出多属性群决策方法;Bao考虑决策者对犹豫不决度的偏好,定义了直觉模糊集的熵和交叉熵测度,提出了一种基于前景理论和证据推理方法的直觉模糊决策方法。因此,采用证据推理方法对含有较强犹豫性、模糊性和不确定性的决策信息进行集结,能较好地保证决策信息的完整性。
综上所述,上述学者分别从不同角度提出了直觉模糊熵的公理化定义,有利于实现直觉模糊多属性决策。然而现有的公理化定义描述部分直觉模糊集的不确定性特征并不准确或者不全面,例如不能区分(0.5,0.5)、(0.4,0.4)这类隶属度与非隶属度相等直觉模糊集的模糊性,导致部分文献定义的直觉模糊熵公式在某些情形下不能精确度量熵值,进而影响多属性决策结果。于是,研究首先分析了现有直觉模糊熵公式与不确定性的匹配度,在完善直觉模糊集不确定性度量问题的基础上,改进了直觉模糊熵公理化定义,进而构造一类改进的直觉模糊熵公式,提出一种基于改进直觉模糊熵和证据推理的多属性群决策方法,最后利用算例分析阐明方法的有效性。
1 直觉模糊熵的改进
1.1 直觉模糊熵的概念与分析
定义
1 若E
满足如下准则,称实值函数E
:IFS
(X
)→[0,1]为直觉模糊熵。条件1:E
(A
)=0当且仅当A
是经典集;条件2:E
(A
)=1当且仅当∀x
∈X
,有μ
(x
)=υ
(x
);条件3:E
(A
)=E
(A
);条件4:当μ
(x
)≤υ
(x
)时,有μ
(x
)≤μ
(x
),υ
(x
)≥υ
(x
);或当μ
(x
)≥υ
(x
)时,有μ
(x
)≥μ
(x
),υ
(x
)≤υ
(x
),则都有E
(A
)≤E
(B
)成立。基于以上常用的直觉模糊熵的定义,Szmidt,Verma,Yuan,陈业华和王坚强等给出了不同的直觉模糊熵公式,分别记为E
(A
)-E
(A
),具体公式如下:
(1)

(2)
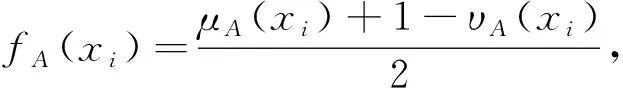
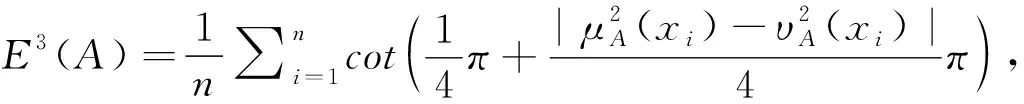
(3)

(4)

(5)
E
(A
)-E
(A
)均根据上述公理化定义构造,部分学者对约束条件做出了改进,如赵飞、高明美将改进的直觉模糊熵记为E
(A
)和E
(A
),如式(6)、式(7)所示。
(6)

(7)
上述的E
(A
)-E
(A
)在一定范围内具有适用性,但还存在部分缺陷,具体分为两个方面。(1)最大直觉模糊熵的取值问题。根据定义1中条件2,直觉模糊集中的隶属度等于非隶属度时不确定度最高,直觉模糊熵达到最大值。忽略了实际决策时支持与反对信息虽然相同,但依旧包含着部分有效信息的情况。因此将定义1中条件2修改为,当隶属度与非隶属度相等且为0时,直觉模糊熵达到最大值更为合理。
(2)忽略犹豫度的影响。犹豫度相等时,直觉模糊熵与隶属度和非隶属度的差值负相关,即差值越小表示不确定程度越高,熵值越大;隶属度与非隶属相等且不为0时,犹豫度越大代表不确定性越大,熵值也越大。另外,直觉模糊集的不确定性除了来自未知信息,即犹豫度的影响,还包括直觉模糊集中已知信息的模糊度。因此直觉模糊集的不确定性必定不会小于犹豫度。可将定义1的条件扩展以便更好地描述直觉模糊熵。
1.2 改进直觉模糊熵的提出
综上分析,对已有的直觉模糊熵公理化定义做出以下改进与拓展。
定义
2 若E
满足如下准则,称实值函数E
:IFS
(X
)→[0,1]为直觉模糊熵。条件1:E
(A
)=0,当且仅当A
是一个分明集;条件2:E
(A
)=1,对∀A
∈IFS
(X
),当μ
(x
)=υ
(x
)=0时成立;条件3:当π
(x
)=π
(x
)时,若|μ
(x
)-υ
(x
)|≤|μ
(x
)-υ
(x
)|,则E
(A
)≥E
(B
);或当|μ
(x
)-υ
(x
)|=|μ
(x
)-υ
(x
)|时,若π
(x
)≥π
(x
),则E
(A
)≥E
(B
);条件4:当μ
(x
)≤υ
(x
)时,有μ
(x
)≤μ
(x
),υ
(x
)≥υ
(x
);或当μ
(x
)≥υ
(x
)时,有μ
(x
)≥μ
(x
),υ
(x
)≤υ
(x
),则E
(A
)≤E
(B
);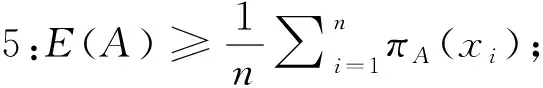
E
(A
)=E
(A
)。由此基于定义2,研究构造一类改进直觉模糊熵公式,以便较好区分直觉模糊集的模糊性。对于任意的直觉模糊集{[x
,μ
(x
),υ
(x
)]|x
∈X
,i
=1,2,…,n
},π
(x
)=1-μ
(x
)-υ
(x
)代表犹豫度。定义直觉模糊熵: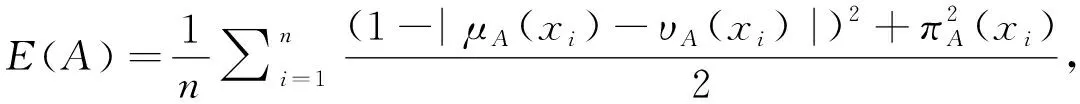
(8)

(9)
下面证明研究提出的熵符合定义2中的6个约束条件:


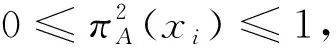
μ
(x
)=υ
(x
)=0,则可得E
(A
)=1,因此E
(A
)=1。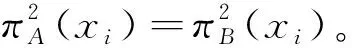


μ
(x
)≤υ
(x
)时,有μ
(x
)≤μ
(x
),υ
(x
)≥υ
(x
),f
(μ
(x
),υ
(x
))≤f
(μ
(x
),υ
(x
));同理,当μ
(x
)≥υ
(x
)时,有μ
(x
)≥μ
(x
),υ
(x
)≤υ
(x
),f
(μ
(x
),υ
(x
))≤f
(μ
(x
),υ
(x
))。因此,当A
≤B
时,则有E
(A
)≤E
(B
),故E
(A
)≤E
(B
)成立。
A
={[x
,υ
(x
),μ
(x
)]|x
∈X
,i
=1,2,…,n
},故E
(A
)=E
(A
)。1.3 改进直觉模糊熵的优势说明
综上分析,改进直觉模糊熵公式符合拓展及修改后的直觉模糊熵公理化定义。从算例和图像两个方面来说明改进的直觉模糊熵的有效性,进而指出其他公式可能存在的缺陷。
(1)从算例来看,分别用E
(A
)~E
(A
)与研究提出的E
(A
)计算以下直觉模糊集(A
~A
),结果如表1所示。从表1可以看出:①E
(A
)和E
(A
)没有将犹豫度考虑进去,用E
(A
)计算犹豫度相等的直觉模糊集(如A
、A
与A
),结果均相等;用E
(A
)计算隶属度与非隶属度差值相等的直觉模糊集(如A
和A
),结果相等。根据定义2中条件3可知,E
(A
)>E
(A
)>E
(A
),E
(A
)>E
(A
)结果合理。②用E
(A
)~E
(A
)计算隶属度与非隶属相等且不为0的直觉模糊集(如A
、A
与A
),计算结果均为最大值。根据定义2中条件2和条件3可知,E
(A
)<E
(A
)<E
(A
),结果合理。③E
(A
)和E
(A
)存在对部分直觉模糊集无法区分的缺陷,如E
(A
)对A
和A
、E
(A
)对A
和A
在区分不确定度时失效。但E
(A
)可清晰区分。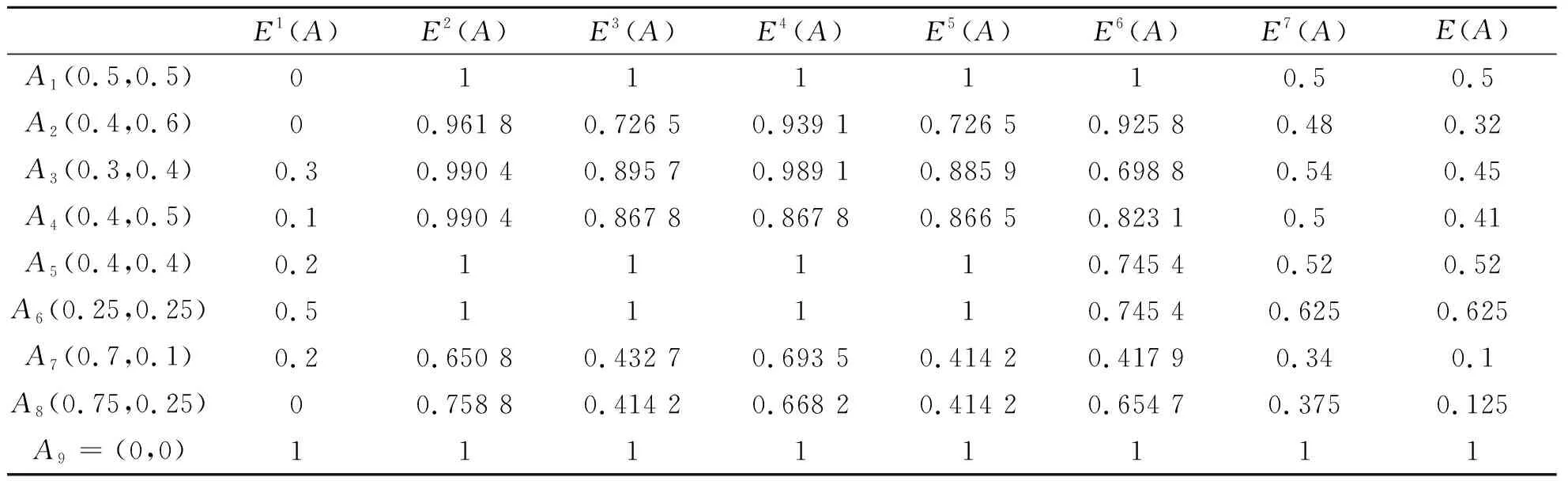
表1 不同直觉模糊熵值的比较
(2)从图像来看,E
(A
)~E
(A
)与研究提出的E
(A
)的三维图像如图1~图8所示。由图1~图8可以看出:①当μ
(x
)=υ
(x
)=0时,E
(A
)~E
(A
)及E
(A
)都取得最大值1,并且E
(A
)~E
(A
)及E
(A
)的图像都具有对称性。②从图1~图6可以看出,它们都有两个及两个以上的点对应着最大值1或最小值0,因此可能存在对不同的直觉模糊集的不确定性度量不精准的问题。而图7、图8较为类似,但E
(A
)在区分隶属度或非隶属度为0.5的直觉模糊集时失效,而由图8可以看出不同的直觉模糊集所对应的E
(A
)均不同,表明E
(A
)具有较好的区分性,不会出现熵值相同情况。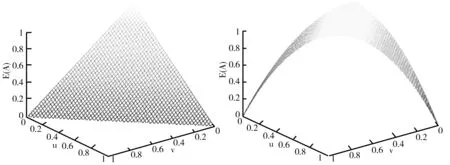
图1 E1(A)三维函数图 图2 E2(A)三维函数图
综上所述,根据修改后的直觉模糊熵公理化定义构建的E
(A
)可较好弥补上述公式的不足,区分直觉模糊集的模糊性时具有合理性和有效性。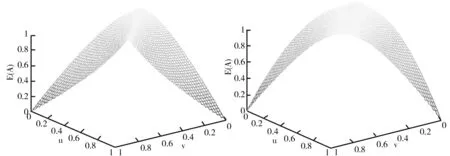
图3 E3(A)三维函数图 图4 E4(A)三维函数图

图5 E5(A)三维函数图 图6 E6(A)三维函数图
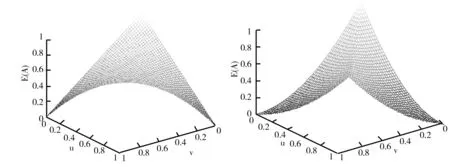
图7 E7(A)三维函数图 图8 E8(A)三维函数图
2 直觉模糊多属性群决策方法
针对决策信息为直觉模糊数,且属性权重与专家权重完全未知或属性权重与专家权重部分已知的多属性决策问题,首先,依据改进的直觉模糊熵对决策矩阵中属性的不确定性进行度量,求出属性权重和专家权重,利用证据推理方法进行信息的融合,并根据与理想解的Hamming距离进行排序。具体决策过程如下:

Step 1 属性权重的求解。
越小的直觉模糊熵值意味着更小的不确定程度和更多的确定性信息,属性的权重应使得所有属性的总熵值最小,H
表示属性权重已知的约束条件集合,由此建立权重优化模型如下: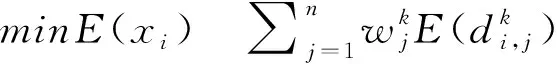
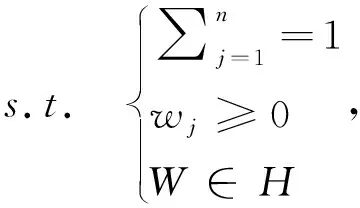
(10)
在属性权重完全未知的情况下,得到属性权重为:
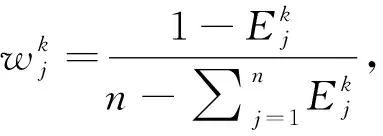
(11)
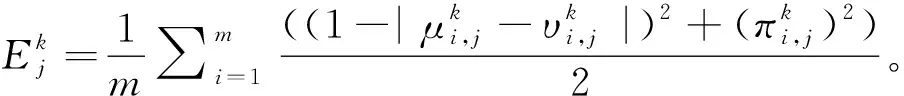
(12)
Step 2 基于证据推理的综合直觉模糊集的形成。

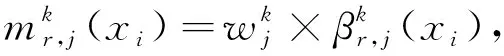
(13)

(14)

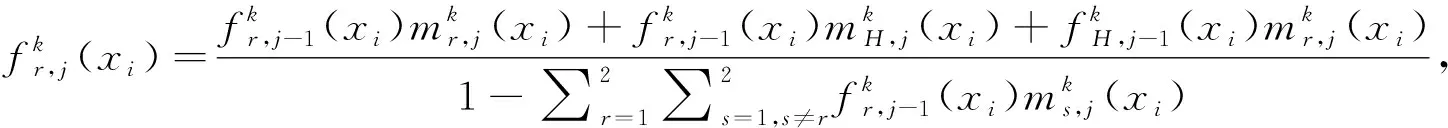
(15)
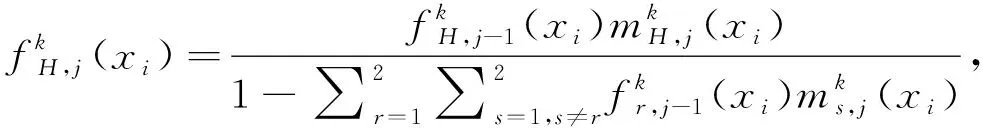
(16)
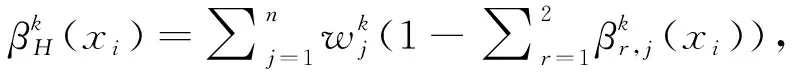
(17)
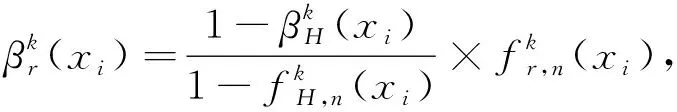
(18)

(19)

Step 3 基于综合直觉模糊熵值的专家权重求解。
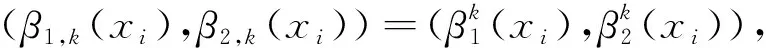

(20)
Step 4 最终直觉模糊集形成。
依据Step 2求得方案x
的支持度β
(x
)及未分配等级的β
(x
),可得最终决策矩阵Q
=(q
)×1,q
=(β
(x
),β
(x
))。具体公式如下: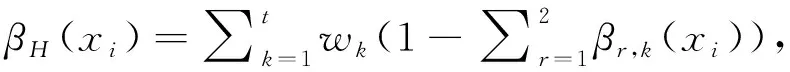
(21)
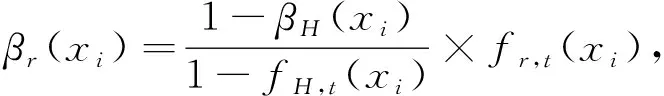
(22)
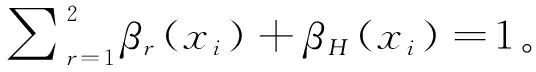
(23)
Step 5 计算各方案与理想解的相对贴近度,最后选择最佳方案。
正理想点记为X
=(1,0),负理想点记为X
=(0,1)。方案x
的最终直觉模糊值与正、负理想方案之间的Hamming距离为: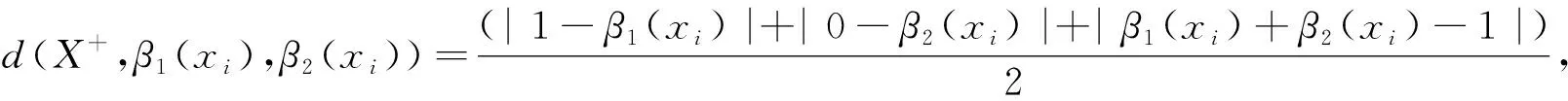
(24)

(25)
式中,d
(X
,β
(x
),β
(x
))∈[0,1],0≤β
(x
)+β
(x
)≤1,0≤β
(x
)≤1,0≤β
(x
)≤1,1≤i
≤m
。各方案与理想解的相对贴近度S
如式(26)所示。
(26)
按照相对贴近值从大到小对方案进行排序,相对贴近度越大的方案越好。
3 算例分析
采用文献[16]的案例数据来验证研究方法的合理性,3个专家(P
~P
)对4个候选人(x
~x
),从工作态度、学术能力、教学经验和品德4个方面(C
~C
)进行打分,最终挑选出最优者。运用式(10)~式(12)计算不同专家的属性权重,结果如表2所示。

表2 各专家决策信息及属性权重
根据表3,运用式(13)~式(25)求得最终决策结果与排序,并与文献[16]方法做比较,结果如表3所示。由表3可以看出:①研究方法求得最佳的候选人是x
,其次是x
,与文献[16]相比两种方法求得的最优候选人结果是一致的,说明研究方法的可行性。②研究方法与文献[16]比较而言,x
和x
评价结果有所差别,差异的原因是两种方法采用的直觉模糊熵不同,导致求得属性和专家权重不同从而影响排序结果。文献[16]方法中采用了1.1中所提到的E
(A
),但由1.3中表1与三维函数图像分析表明,E
(A
)在区别隶属度与非隶属相等且不为0的直觉模糊集(如A
(0.5,0.5)、A
(0.4,0.4)和A
(0.25,0.25))时失灵,研究方法采用的E
(A
)在特定情形下对直觉模糊集不确定程度的度量要优于E
(A
),因此,研究方法在解决直觉模糊多属性决策问题时比文献[16]方法更为合适。
表3 研究方法与文献[16]决策结果的比较
为了进一步验证方法的科学性和合理性,将研究方法与文献[6]中算例进行对比。通过3个专家依据5个评价指标对4家供应商进行选择,两种方法进行求解的计算结果如表4所示。通过决策结果可以看出,研究方法与文献[6]方法挑选的最优供应商都是x
。文献[6]方法是利用算子解决直觉模糊多属性决策问题,研究方法是从直觉模糊熵来刻画不确定性,再利用证据理论对不确定信息融合的方法解决直觉模糊多属性决策问题。虽然两者方法不同,但是最优结果相同,从一定程度上说明了研究方法的可行性和合理性。
表4 研究方法与文献[6]决策结果的比较
4 结论
为解决决策信息为直觉模糊数且属性权重或专家权重完全未知与部分已知的多属性决策问题,提出一种基于改进的直觉模糊熵和证据推理的决策方法。研究在进一步完善了直觉模糊熵公理化定义的基础上,设计了一类改进的直觉模糊熵公式,克服了在某些情形下不能区分和度量直觉模糊集的不确定性问题,为解决直觉模糊多属性问题提供思路,最后通过与文献[16]的比较说明了研究方法的可行性。研究模型没考虑区间型和梯形的直觉模糊数,针对这两种直觉模糊熵的度量也是未来进一步研究的方向。
