直流配电网的三点估计概率潮流计算方法

鄂 霖，马 振，肖 宇，朱永强

(新能源电力系统国家重点实验室(华北电力大学)，北京市 昌平区 102206)

0 引言

近年来，随着人们对能源问题的重视程度不断提高，分布式电源、电动汽车和储能等技术的使用逐渐广泛。这些新型的发电技术和负荷需求，大多数都存在直流环节。相比于接入交流配网，采用直流配网可以减少大量环流环节，减少损耗，提高经济效益[1-2]。但是，这些技术给配电网注入了新的不确定因素，影响配电网的电压分布和安全运行，因此有必要研究在不确定因素影响下的直流配电网稳态潮流问题[3-4]。概率潮流(probabilistic load flow, PLF)适用于处理具有一定分布规律的不确定性问题，最早由B.Borkowska在20世纪70年代提出，此后大量学者对含不确定性的潮流问题做了详细的研究。

目前，概率潮流研究内容集中在计算方法的研究[5-6]，主要分为3类，包括模拟法[7-9]、解析法[10-11]和近似法[12-14]，3种求解方法各有其优缺点。模拟法计算规模大、结果精确但计算速度较慢，经常作为其他方法比较对象。文献[8]采用的超拉丁立方采样法，提高了采样的效率，相较于传统蒙特卡洛法[7](montecarlo simulation，MCS)，减少了计算的次数；文献[9]将超拉丁采样方法与神经网络相结合，提出一种更适于大规模网络节点的计算方法。解析法将求解概率问题中涉及到复杂的卷积运算转变为半不变量间的数值运算，极大地提高了运算效率，可以求解输出变量概率密度分布，但是计算精度较差。文献[10]使用改进的混合高斯模型建立了概率潮流的解析算法，考虑了大规模风电接入时的相关性系数，但没有考虑其他分布式电源的接入；文献[11]采用的广义半不变量法，计算交流概率潮流时计及分布式电源的下垂系数模型，但没有涉及直流侧的研究。近似法求解概率潮流不需要大规模的运算，根据随机变量的多阶矩，给出潮流运算输出变量的概率特征，但是不能得到输出变量的概率分布，其中点估计法(point estimate method，PEM)具有运算速度快，精确性高的特点，运用得最为广泛。文献[12]提出了一种将Nataf逆变换于三点估计相结合的概率潮流算法，根据半经验公式处理Nataf变换中的相关系数问题；文献[13]提出了一种改进的点估计算法，减小了系统规模增加对于三点估计法精度的影响；文献[14]通过构造二元copula函数，拟合更加精确的输入随机变量概率模型。此外，还有学者在不同方面对概率潮流做了详细的研究[15-16]，但对于直流配电网的概率潮流研究还比较少。

含分布式电源的直流配电网的研究多集中于换流器模型的建立[17-18]以及含多电压等级时的计算方法[19]。本文针对具有分布式电源和随机负荷接入的直流配电网，将三点估计法与交直流混合的直流配电网潮流计算相结合；研究与蒙特卡洛法相比计算效率的变化和新能源接入增多时计算方法的精确程度是否变化，同时将直流系统与交流系统的概率潮流的误差作比较；最后研究当风能和光伏分别单独增加时，本文所提方法误差的变化，以此说明消纳新能源在一定范围内时本文所提方法计算程度的精确性。

1 随机变量概率模型

1.1 风力发电概率模型

风力发电系统通过风机把风能转化为电能。风速是一种不确定的变量，研究表明多数地区风速的分布规律都符合Weibull分布[20]，其中广泛采用的是双参数Weibull分布，Weibull分布的概率密度函数(probability density function，PDF)数学表达式如下：

(1)

式中：v为风速；c和k分别为Weibull分布的比例参数和形状参数。风电场的输出功率Pw与风速v相关[18]，其数学模型如下：

(2)

式中：vin、vout、vr分别为风力发电机的切入风速、切出风速和额定风速；Pw和Pr分别为风机的实际输出功率和额定功率。

1.2 光伏发电概率模型

太阳能发电系统通过光伏电池板把光能转化为电能。光照强度也是一种不确定的随机变量，研究表明光照强度r的分布规律符合Beta分布[21]，Beta分布的PDF数学表达式如下：

(3)

式中：a和b为Beta分布的状态参数；rmax为当地的最大光照强度；Γ为Gamma函数。

光伏发电系统的输出功率PW与当地的光照强度r有关，可以用如下的数学公式表示：

PW(r)=ηSr

(4)

式中：η为转化率；S为光伏机组的总面积。

1.3 随机负荷概率模型

在直流配电网中，主要的负荷包括居民用电、电动汽车和储能设备等。根据研究可知，这些负荷服从正态分布[6,9,22]，其PDF表达式如下：

式中：μP、σP分别为有功输出的期望和方差；μQ、σQ分别为无功输出的期望和方差。

1.4 燃气轮机概率模型

采用通用的简化模型，假设燃气轮机组只有正常运行和停运2种状态，认为其服从0-1分布的离散概率模型[21]，表达式如下：

式中：pi为该燃气轮机组的可利用率；Pr为该机组的有功额定功率；Qr为该机组的无功额定功率。

2 直流配电网潮流计算

2.1 AC-DC换流环节

交流主网、交流分布式电源和交流负荷通过AC-DC换流器接入直流配电网，因此需要建立AC-DC换流器的交直流潮流模型[17]，如图1所示。

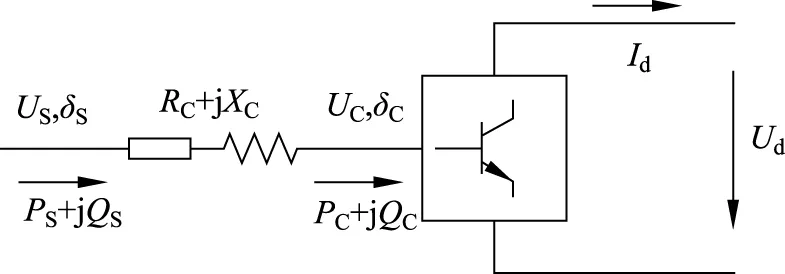
图1 AC-DC换流器潮流模型Fig.1 AC-DC converter power flow model

图中：US、δS为系统侧电压有效值和相角；UC、δC为换流器侧电压有效值和相角；PS、QS为系统注入的有功功率和无功功率；PC、QC为交流侧向换流器注入的有功功率和无功功率；RC和XC为换流器的等效电阻和等效电感；Ud为直流侧电压；Id为直流侧电流。

将AC-DC的稳态潮流模型分为交流侧模型、直流侧模型以及交直转换模型。其中，交流侧模型为：

式中：UC、δC、PC、QC为待求变量。

直流侧模型为

Pd=UdId

(13)

交直转换环节为

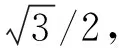
式中：a0、a1、a2分别表示换流器固定损耗、一次损耗、二次损耗的系数。

根据不同的控制策略，换流器直流侧节点在直流配电网中设置为不同的节点类型。当设置为定直流电压控制时，直流侧为V节点，此时由直流侧向交流侧迭代；当设置为定直流功率控制时，直流侧为P节点，由交流侧向直流侧迭代。

2.2 DC-DC换流环节

在同一个直流配电网中，可能会存在多个电压等级的子配电网。因此，需要DC-DC变换器把不同电压等级的配电网连接起来进行功率的传输。DC-DC变换器分为不带隔离变压器的变换器和带隔离变压器的变换器。不带隔离变压器的DC-DC变换器包括Boost变换器、Buck变换器和Boost-Buck变换器；带隔离变压器的DC-DC变换器包括正激变换器、反激变换器和全桥变换器。对于中压侧的配电网而言，单个DC-DC变换器的耐压水平、传输功率的能力有限。因此由中压配电网向低压配电网传输功率时，可以采用串联输入并联输出(input-series output-parallel，ISOP)的拓扑结构，见图2。

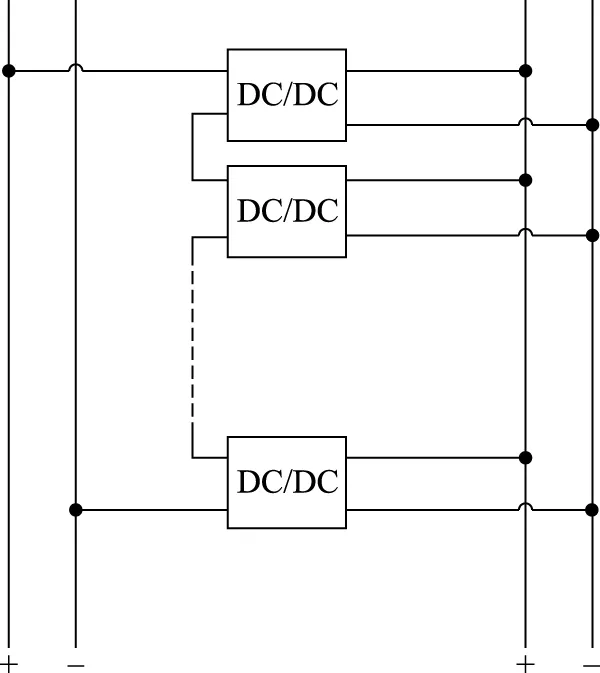
图2 DC-DC串联输入并联输出(ISOP)Fig. 2 DC-DC series input and parallel output

由文献[23]提出的DC-DC变换器建模方法，当DC-DC电路工作在连续电流模式时(continuous current mode，CCM)，建立了它们在稳态时的统一潮流模型。如图3所示，实际的DC-DC变换器可以看作由理想的直流变压器、内部阻抗和一个反向电压源串联组成。

图3 DC-DC变换器的等效电路Fig.3 Equivalent circuit of DC-DC converter

与交流电网中处理变压器模型类似，可以将DC-DC支路等效为一个π型电路，如图4所示。

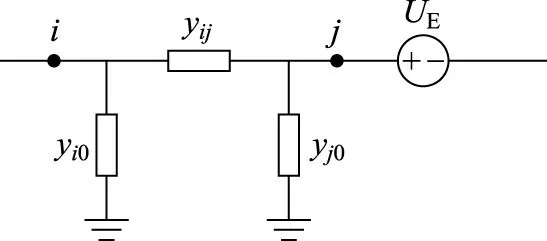
图4 DC-DC支路的π型电路Fig. 4 π-type circuit of DC-DC branch

经推导可得：

(18)

2.3 潮流计算流程

与交流电网不同，直流配电网中的电气量只有电压、电流和有功功率，不包括相角和无功功率。因此，把直流网中的节点划分V节点和P节点。V节点是给定节点电压的节点，包括通过定电压控制的电力电子变换器与交流主网、分布式电源相连接的节点；P节点是给注入的节点，包括通过定功率控制变换器与交流电网、分布式电源、储能设备和交流负载连接的节点，以及恒功率模型的直流负荷节点。在潮流计算过程中，如果发生功率越限的情况，一般把V节点转化为P节点继续求解。

在给定电网的参数后，建立节点导纳矩阵，用牛顿-拉夫逊法进行求解功率方程。值得注意的是，由于DC-DC支路上存在压降UE，因此要对注入电流进行修正。设DC-DC支路首、末端节点的集合分别为I、J，则注入电流的修正方程[24]如下：

(19)

式中：I0为修正前的节点注入电流；I为修正后的节点注入电流。假设系统的V节点为1,2,…,m，P节点为m+1,…,n。则系统的功率方程为

ΔP=PG-PL-(diagU)YI

(20)

式中：ΔP为节点修正功率列向量；PG为节点注入功率列向量；PL为节点负荷功率列向量；Y为系统节点导纳矩阵；diagU为系统节点电压对角矩阵。可得到修正方程为

(21)

式中：J为有功功率P相对节点电压U的雅克比矩阵[17]；其余部分与用牛拉法计算交流电网潮流类似，给定初值，通过迭代计算得到P节点电压，由系统的电压分布计算线路潮流和V节点注入功率。

3 概率潮流计算

3.1 随机变量的处理

假设存在一组随机变量X=[x1，x2，…，xn]，其中随机变量xi的PDF和累积分布函数(cumulative distribution function，CDF)分别为fi(xi)和Fi(xi)，X的线性相关矩阵为ρ。通过式(22)可以得到从X到Y的单射，其中Y=[y1，y2，…，yn]为一组标准正态分布的随机变量。

yi=Φ-1[Fi(xi)]

(22)

式中Φ-1为标准正态分布的CDF逆函数。

若Y的线性相关矩阵为ρ′，ρ和ρ′每个位置的元素分别为ρij和ρ′ij,二者的值应满足如下关系式：

(23)

式中：μi和μj分别为随机变量xi和xj的期望值；σi和σj分别为xi和xj的标准差；Φ(xi,xj,ρ′)为具有相关系数的二维标准正态分布的联合分布函数。用数值求积的方式求取ρ′ij计算量比较大，可以采用文献[25]中的近似方法进行计算，最终得到结果的误差也在可接受范围内。上述将一组任意分布且相关的随机变量X转化为一组互相独立的标准正态随机变量Y的过程称为Nataf变换，同理可以通过其逆过程将Y转化为X。

由于点估计法中必须采用不相关的随机变量，可以通过式(24)对ρ′进行Cholesky分解，得到下三角矩阵C。由式(25)得到互相独立的标准正态分布的随机变量组Z。

3.2 三点估计法

假设D=[d1，d2，…，dn]为n维输入随机变量，G=[g1，g2，…，gm]为m维输出随机变量，它们之间满足：

G=H(D)

(26)

对于直流配电网而言，输入随机变量有风场的风速v，光伏场的光照强度r，以及每个节点上的随机负荷P、Q。输出随机变量包括P节点和I节点的节点电压U，支路潮流Pij，以及V节点的注入功率P0；H表示潮流方程。

对于每一个随机输入变量di，取3个采样点di,k(k=1,2,3)，采样点的选取由式(27)—(29)确定。

di,k=μi+ξi,kσi,k=1,2,3

(27)

式中：μi和σi分别为随机变量di期望值和标准差；ξi,k为位置系数，其数学表达式[12]为：

式中：vi和λi分别为随机变量xi偏度系数和峰度系数。当di每取一个采样值时，其余的输入随机变量都取均值，此时由式(15)计算一组输出随机变量G(i,k)=H(μ1，…，μi-1，di，μi+1，…，μn)，一共应该计算3n次。但可以看出当k=3时，所有输入随机变量均为均值，有n次的计算结果是相同的，故实际只用计算2n+1组输出随机变量G的值。

同时，对于每一组G(i,k)计算一个对应的权重系数为

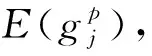
(32)

E(·)表示数学期望算子，在求出输出随机变量gj的前两阶原点矩后，即可估计其期望值μj和标准差σj。

3.3 计算流程

根据3.1节和3.2节的内容，将Nataf逆变换和三点估计法相结合，在给定任意分布的输入随机变量下，且计及其相关性时，可以得到一种快速估计出输出随机变量的数字特征的方法，三点估计法计算流程如图5所示，具体步骤如下文所述。

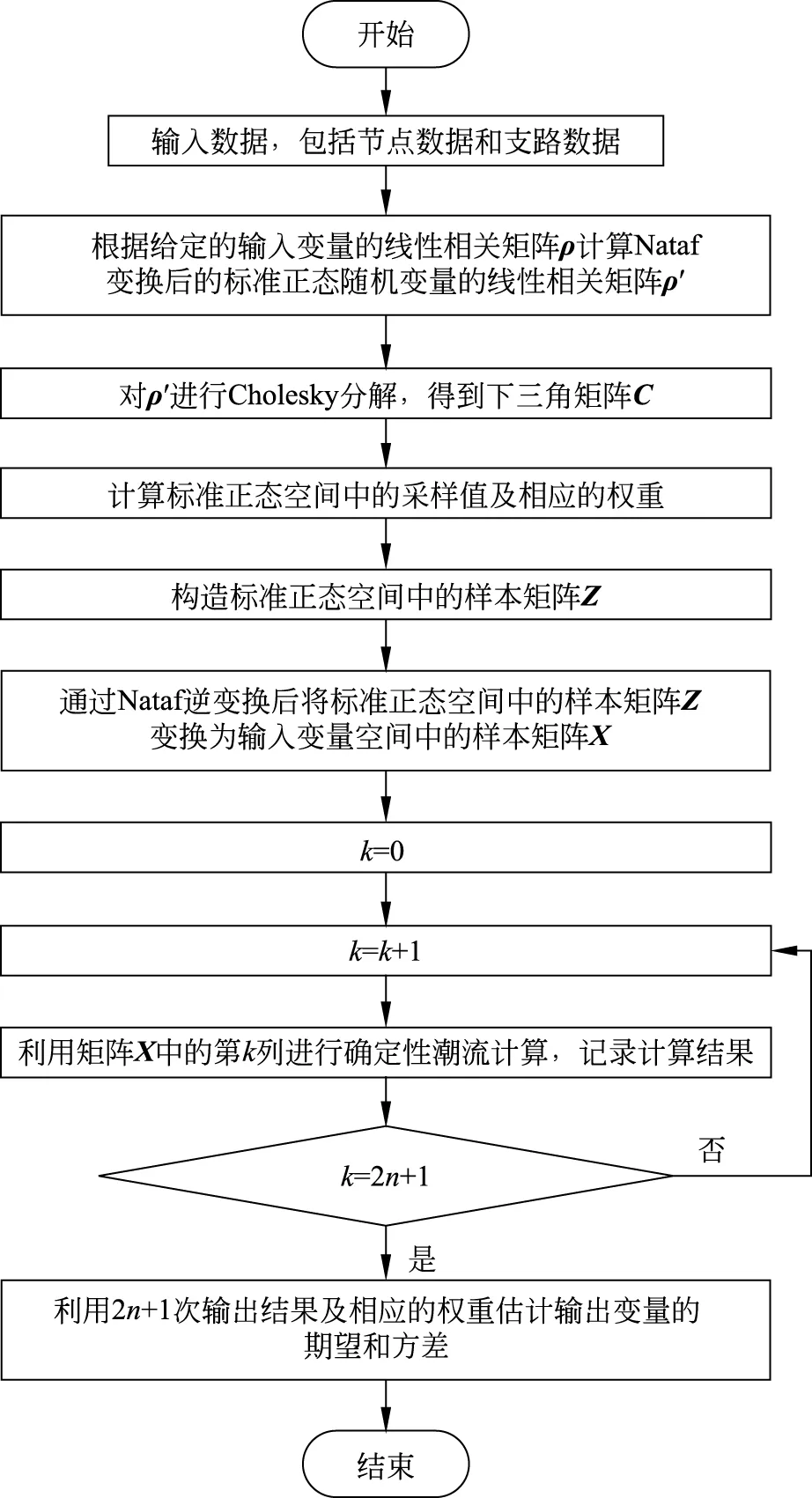
图5 三点估计法计算流程Fig.5 Calculation flow chart of Three-point estimation

步骤1) 根据输入随机变量X的线性相关系数矩阵ρ计算Nataf变换后的标准正态分布Y的线性相关矩阵ρ′。再由式(24)对进行Cholesky分解，得到下三角矩阵C。

步骤3) 由式(25)得到具有相关系数的标准正态分布Y，通过Nataf逆变换将Y映射到原始输入随机变量X。

步骤4) 将X带入式(26)，进行2n+1次计算，得到2n+1组G的评价值。通过式(32)到式(34)估计G的期望值和标准差。

4 算例分析

本文采用如图6所示的改造IEEE 14节点直流配电网系统作为算例，整个配电网具有10 kV和380 V两种电压等级，其中1至5节点为10 kV母线，6至12节点为380V母线，不同电压等级的母线间通过DC-DC换流器相连。母线1与交流主网相连，母线10接入1台微型燃气轮发电机组，AC-DC变流器的参数和损耗系数设置见表1和表2。

表1 AC-DC变换器参数Table 1 parameters of AC-DC converter

表2 AC-DC变换器损耗系数Table 2 Loss coefficients of AC-DC converter

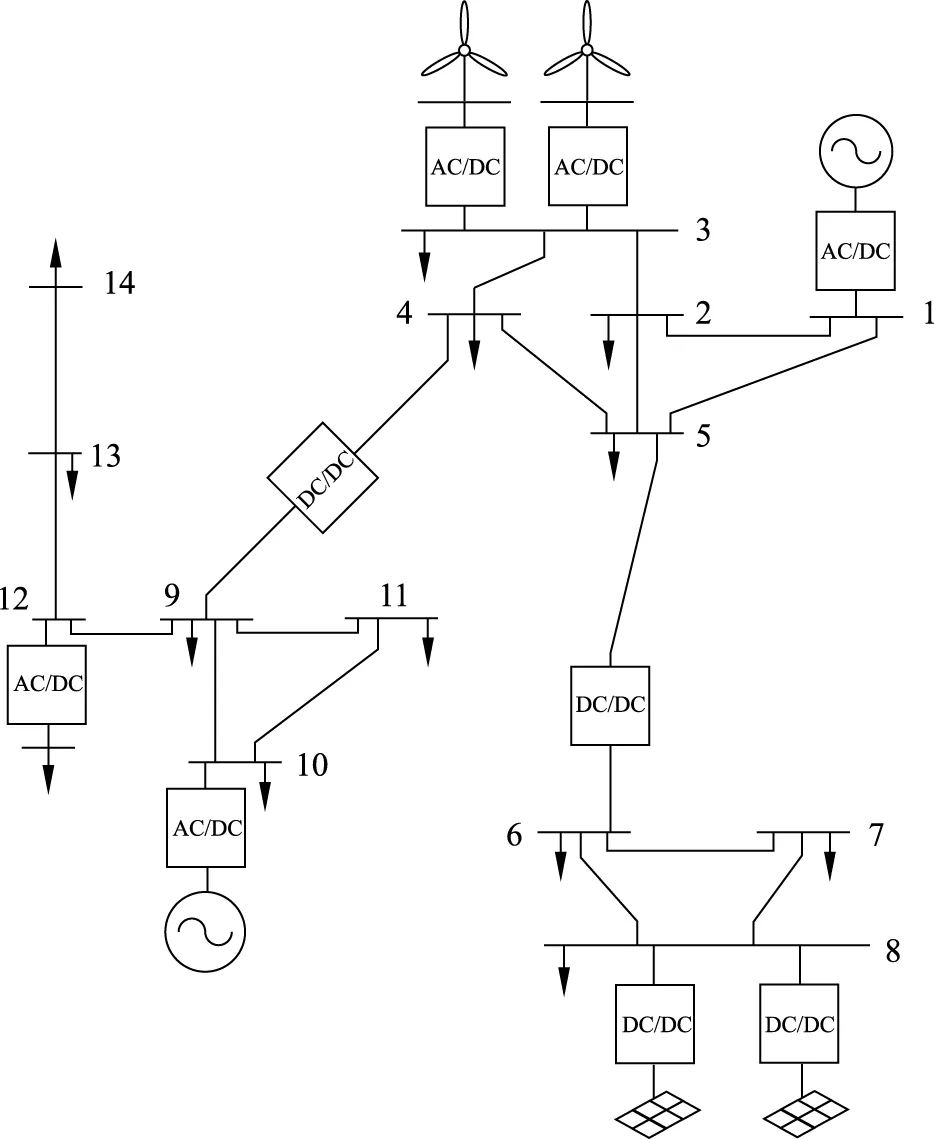
图6 直流配电网弱环连接示意Fig.6 weakly looped structure of DC distribution network

节点3接入2个风力发电厂，风速服从Weibull分布，风电厂1的比例参数为10.5、形状参数为4.0，风电厂2的比例参数为8.5、形状参数为2.2，2个风场之间的相关系数为0.8。风力发电机组的切入风速为4 m/s、切除风速为24 m/s、额定风速为15 m/s，风电场的额定功率均为1.5 MW。节点8接入2个规格相同的光伏电厂，光强服从Beta分布，其中a参数为0.68，b参数为1.82，2个光场之间的相关系数为0.6。光伏电厂的最大光照强度为1.2 kW/m2，光电转化率为0.18，最大输出有功功率为150 kW。

本文将该系统的负荷分为3个区域，其中1至5节点为区域Ⅰ，6至8节点为区域Ⅱ，9至12节点为区域Ⅲ。负荷均服从正态分布，异变系数为0.05。若2个负荷位于同一区域，则相关系数为

0.8，若不为同一区域，则相关系数为0.4。

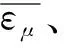
与交流电网相比，直流配电网的潮流计算所含变量更少，且连接的换流环节更少。为了研究三点估计法作用于直流配电网和交流配电网的区别，将三点估计算法同时应用于规模相同的交流系统和直流系统，由于直流系统不含有无功和相角，主要观察他们的电压期望值相对误差和标准差相对误差。如图7所示，交流系统和直流系统的电压期望值相对误差相近且都小于0.1%，说明在直流系统中，应用三点估计法对电压期望值的估计可以取得在交流系统中同样好的估计效果，但是由于误差的数量级过小，此时交流系统和直流系统在计算精度上并无明显区别。如图8所示，当误差的数量级增加时，直流系统电压的标准差相对误差基本上小于交流系统中的值，且均保持在5%的范围以内，说明在估计电压的标准差时，直流系统的三点估计法精确程度要优于交流系统。

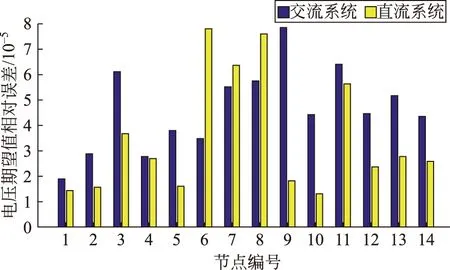
图7 交流系统与直流系统电压期望值相对误差对比Fig.7 Comparison to relative error of voltage expected value between AC system and DC system

图8 交流系统与直流系统电压标准差相对误差对比Fig.8 Comparison to relative error of voltage standard deviation between AC system and DC system

在CPU为Intel(R)Core(TM)i7—6700HQ、主频为2.6 GHz，内存为8 GB的计算机上，采用MATLAB R2016b运行编制的程序计算直流配电网的概率潮流，三点估计法的计算耗时为0.036 s，样本容量为5 000的蒙特卡洛法计算耗时为15.87 s，算法耗时约为点估计法的440倍，说明本文所提方法能够极大地提高对不确定性直流配电系统状态估计的计算效率。在相同网络规模下的交流系统概率潮流运算中，三点估计法的计算耗时为3.139 0 s，样本容量为5 000的蒙特卡洛法计算耗时为551.914 s，说明相较于交流电网，直流电网的概率潮流运算精度与交流电网接近，且运算效率更高。

为了评价系统消纳新能源的程度增加时，点估计法计算结果的准确程度，将该系统分布式电源的额定功率之和与系统负荷的额定功率之和的比值定义为源荷比λ，以λ为参考指标，观察λ约为33%、80%、120%时评价指标的变化。

对表3和表4的数据进行分析可以看出，随着λ的增大，整体数据的相对误差都在增大，说明当系统消纳的新能源增加后，引入的不确定量的波动范围变大了，使得点估计法的估计结果不准确性增加。从变量类别的角度分析，节点电压的期望值误差和标准值误差数量级小于低于线路潮流和线路损耗的期望值误差和标准值误差。从误差类型的角度分析，当λ增大时，期望值误差的增长速度的增加倍率要高于标准值误差的增长速度的增加倍率，特别的，当λ增加到一定程度时，线路潮流和线路损耗的期望值误差的个别值会比较大，使得最大值明显高于平均值，但误差的平均值还在可以接受的范围内。原因是DC-DC等效支路的导纳较小，该类支路传输功率会明显小于非DC-DC支路，使得估计的固有误差相较于估计值自身的占比过大，可以通过改进DC-DC控制方式，增加DC-DC支路的传输能力解决。

表3 不同源荷比时期望值相对误差Table 3 Relative error of expected value when different ratio of power to load

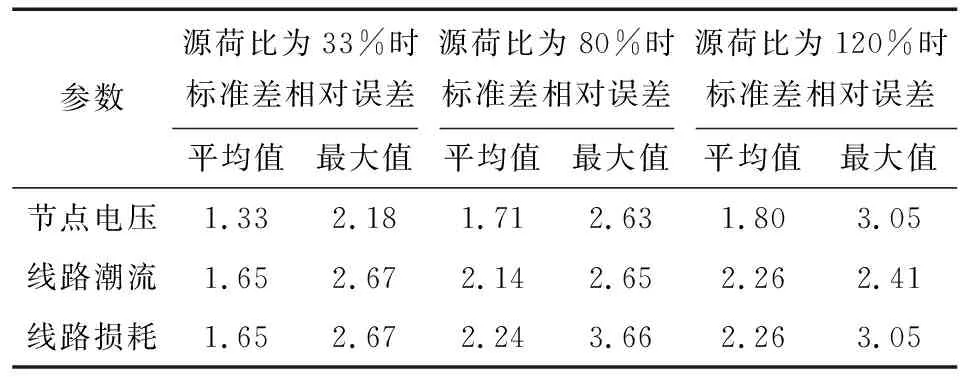
表4 不同源荷比时标准差相对误差Table 4 Relative error of Standard Deviation when different ratio of power to load

进一步研究风电和光伏各自增加时对本文所提算法精度的影响，观察风电或者光伏的装机容量单独增加时节点电压和线路潮流期望值相对误差的变化情况，分别如图9和图10所示。

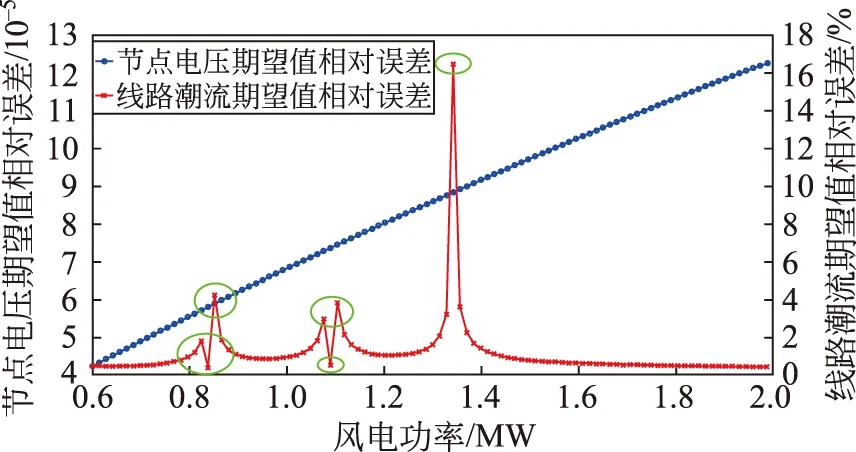
图9 风电功率增加时期望值误差的变化Fig.9 Changes in error of expected values when wind power increases

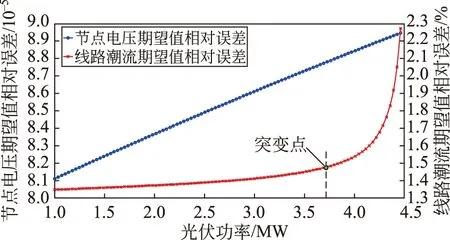
图10 光伏功率增加时期望值误差的变化Fig.10 Change in error of expected values when photovoltaic power increases

分析并对比图9和图10可以看出，当风电和光伏2种不同的新能源容量分别增加时，对线路潮流期望值误差和节点电压期望值误差的影响是不同的。对于节点电压期望值误差而言：当风电或者光伏增加时，估计误差呈线性增加的趋势，而不是爆发增长的趋势，这使得对于节点电压估计的误差始终处于可接受的范围内。而对于线路潮流期望值误差：随着风电或者光伏容量的变化特性不同；对于风电而言，误差与容量变化不存在明显的正相关或者负相关特性，而是对于某些容量值比较敏感，容量在该值附近时较小变化可能导致明显的误差增大或者减小，峰值约为平均值的3倍，由于误差本身的数量级不大，波动中误差还保持在0.2%以内；对于光伏而言，容量和误差的关系呈正相关特性，特别的是，当光伏容量小于某一值时，误差随着容量的增加呈缓慢的线性增长，当光伏容量大于某一值时，误差会迅速增加，为了估计准确性的考虑，应使并网的光伏容量不能高于突变值过多。

5 结语

本文将用于交流系统随机潮流计算的三点估计法推广到含分布式电源的直流配电网潮流计算，考虑了直流配电网中的电力电子元件并结合直流电网的求解模型，提出了一种精确性较好的直流配电网概率潮流计算方法。与蒙特卡洛法作比较，提高了计算效率，保持了计算精度。同时比较同等规模直流配电网和交流配电网的三点估计方法的计算结果，说明本文所提算法更适用于直流系统。最后研究了分布式电源侧的变化对所提所提算法精确程度的影响，并考虑了风电和光伏单独变化时对误差的影响。为未来含分布式电源的直流配电网的发展中，解决不确定性因素引入的问题提供了一种有效的计算和评估工具。