基于模型预测算法的网侧改进直接功率控制策略研究

周云飞，孟克其劳,2,3，温彩凤,2,3，姜宏伟，李超峰

(1.内蒙古工业大学能源与动力工程学院，内蒙古自治区 呼和浩特 010051；2.风能太阳能利用技术教育部重点实验室，内蒙古自治区 呼和浩特 010051；3.内蒙古自治区风电技术与检测工程技术研究中心，内蒙古自治区 呼和浩特 010051；4.太原重工新能源装备有限公司，山西省 太原市 030024)

0 引言

近年来随着分布式风电、光伏等可再生能源大规模接入电网，储能技术得到了长足的发展[1-3]。作为一种新的储能方式，相比于其他储能，飞轮储能功率密度更高、寿命更长、更加环保[4]。近二十年来，飞轮储能技术在国外发达国家已经得到了广泛的应用，目前国内关于飞轮储能技术的应用仍处于示范阶段。其应用领域主要集中在不间断电源、城市轨道交通和电力系统调频调峰。

为了满足电力系统实际应用场景下储能系统容量大、功率高的需求，通常由数台单体飞轮装置并联成飞轮储能阵列系统(flywheel energy storage array system，FESAS)投入运行[5]。在FESAS中，网侧变换器是飞轮储能单元阵列与电网进行能量交换的接口，因此，对网侧变换器的精确控制，是实现飞轮储能阵列系统稳定并网的关键技术之一。国内外许多学者提出了采用电流内环、电压外环的双闭环直接电流控制策略，该控制策略的网侧电流虽然动态响应较为迅速，但直流母线电压响应缓慢，且PI参数整定困难，抗干扰性较差[6-9]；文献[10]提出了一种基于自抗扰控制(active disturbance rejection control, ADRC)直接功率控制(direct power control, DPC)的策略，增强了系统的抗干扰性，但本质上仍是通过开关矢量表和滞环控制环节实现控制目的的传统型DPC策略，控制过程复杂，计算也较为繁琐；文献[11]提出了一种以有功和无功功率为内环，直流母线电压平方为外环的解耦控制策略，改善了网侧变换器直流母线电压及瞬时功率的追踪性能，但并未解决传统直接功率控制策略系统开关频率变化的问题；文献[12]提出了一种恒频DPC策略，根本上解决了系统开关频率变化的问题，但动态响应和跟踪调节能力不够好，且控制系统较为复杂；文献[13-14]提出了基于电压矢量选择的模型预测DPC策略，分别在一个控制周期内采用2个和3个电压矢量，均获得了比单个电压矢量更好的控制效果，且固定了系统开关频率，但恒频控制效果较差，控制过程较为复杂。

因此，本文以FESAS网侧电压型变换器为研究对象，结合模型预测控制(model predictive control，MPC)算法和空间矢量脉宽调制(space vector pulse width modulation，SVPWM)技术，提出一种基于模型预测算法的改进直接功率网侧变换器控制策略，固定开关频率，从而简化控制过程；此外该策略使系统在稳态特性得到优化的同时，以保持快速的响应特性。最后，在PSCAD/EMTDC中进行对比仿真，验证该控制策略的优越性。

1 网侧变换器工作原理及数学模型

1.1 网侧变换器工作原理

FESAS网侧变换器的拓扑结构如图1所示。其中：ea、eb、ec分别为网侧三相电压；L、R分别为网侧变换器交流侧的滤波电感和滤波电阻；ia、ib、ic分别为网侧三相电流；ua、ub、uc分别为网侧变换器交流侧的输出电压；C为直流侧缓冲电容；Udc为直流母线电压；RL为机侧等效负载电阻。

图1 网侧两电平变换器拓扑图Fig.1 Grid-side two-level converter topology

FESAS网侧变换器的运行模式取决于网侧相电压和相电流的相位差及自身的幅值大小，其运行模式主要分为3种：1)功率因数为1的整流运行模式，能量从电网流向网侧变换器，电网和网侧变换器之间不存在无功功率的流动；2)功率因数为1的逆变运行模式，能量从网侧变换器流向电网，电网和网侧变换器之间不存在无功功率的流动；3)相位差为90°时的静止无功补偿运行模式，电网和网侧变换器之间存在无功功率的流动[7]。

1.2 网侧变换器数学模型

在网侧变换器拓扑中，根据电路理论中的KVL和KCL基本定律及坐标变换中的克拉克和派克变换，推导出网侧变换器在dq坐标系下的数学模型为

(1)

式中：id、iq分别为网侧电流在dq坐标系下的分量；ed、eq分别为网侧电压在dq坐标系下的分量；ud、uq分别为网侧变换器交流侧输出电压在dq坐标系下的分量；sd、sq分别为开关状态在dq坐标系下的分量。

基于电网电压d轴定向控制技术[15]，依据瞬时功率理论，在电网稳定的条件下，推导出瞬时有功功率和无功功率：

(2)

2 网侧SVPWM MP-DPC控制策略

将MPC算法、DPC策略与SVPWM技术相结合，提出了一种基于SVPWM的模型预测直接功率控制(SVPWM MP-DPC)策略，克服了传统直接功率控制中采样频率要求高、开关频率变化、控制系统复杂、系统有功功率和无功功率耦合、电压矢量作用时间计算繁琐等一系列难题[15-16]。

2.1 功率预测模型

设第k个采样周期有功功率和无功功率的偏差为

(3)

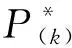
若第k+1个采样周期中有功功率和无功功率的偏差为0，则有：

(4)

式中：P*(k+1)和Q*(k+1)分别为第k+1个采样周期中的参考有功功率和参考无功功率；P(k+1)和Q(k+1)分别为第k+1个采样周期中采样的瞬时有功功率和无功功率。

因此，相邻2个采样周期内有功功率和无功功率的变化量为

(5)

依据电网无功标准Q*给定为0，假设相邻2个采样周期内系统的参考有功功率偏差不变，则有：

(6)

将式(6)代入式(5)，可得：

(7)

由瞬时有功功率和无功功率(式(2))，可得：

(8)

结合式(1)的前2个式子可得：

(9)

将式(9)离散化并作整理可得网侧有功功率和无功功率变化量的预测模型：

(10)

式中：ed(k)为第k个采样周期内网侧电压的d轴分量；id(k)和iq(k)分别为第k个采样周期内网侧电流的d、q轴分量；ud(k)和uq(k)分别为第k个采样周期内交流侧输出电压的d、q轴分量；Ts为采样周期。

为使下一采样周期中有功功率和无功功率的偏差为零，根据上述功率预测模型并结合式(5)、(7)可计算出相应的交流侧参考输出电压u′d(k)和u′q(k)：

(11)

2.2 外环控制模式

外环控制模式为恒压控制，结构为直流母线电压平方外环，该控制策略的特点是在快速稳定直流母线电压的同时能够与上述功率预测模型进行协调控制，进一步改善运行性能。

根据功率计算的定义可得：

(12)

设UD=Udc2，对式(12)整理得：

(13)

采用PI控制器，则有：

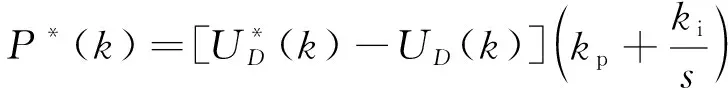
(14)

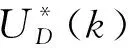
为了验证该策略的有效性，在PSCAD/EMTDC环境下对直流母线电压外环和直流母线电压平方外环的策略进行了仿真研究，结果如图2所示。

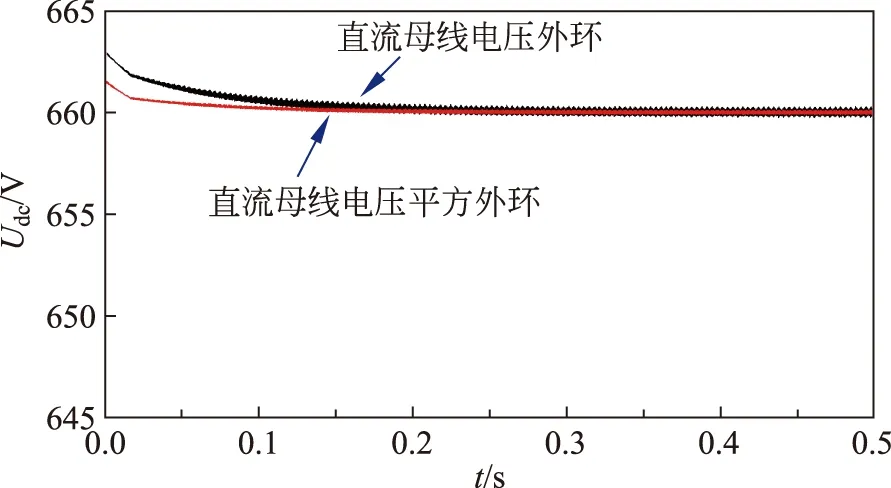
图2 2种策略下直流母线电压对比Fig.2 Comparison of DC bus voltage under two strategies

从仿真结果可以看出，直流母线电压平方外环的控制策略从控制启动至达到稳定阶段所需时间较直流母线电压外环大大缩短，且抖振抑制效果良好，稳态静差几乎为零，跟踪性能较好。

2.3 脉宽调制方式

目前最常用的脉宽调制方式主要有正弦脉宽调制(sinusoidal pulse width modulation，SPWM)和SVPWM。SPWM调制最大输出相电压幅值为Udc/2，直流电压利用率仅为0.866；而SVPWM调制最大输出相电压幅值为Udc，直流电压利用率为1。SVPWM调制比SPWM调制的直流利用率提高了15.47%[17]。此外，SVPWM调制不仅能固定系统开关频率，而且在相同开关频率下输出波形谐波含量更少，因此本文选用SVPWM调制。

SVPWM调制原理为采用2个非零矢量和零矢量来合成所需的指令矢量，从而生成所需要的PWM脉冲信号[18]。

变换器输出电压可由开关信号和直流母线电压表示为

(15)

式中：uα(k+1)、uβ(k+1)分别为第k+1个采样周期中变换器输出相电压在αβ坐标系下的分量；Sa(k+1)、Sb(k+1)、Sc(k+1)分别为第k+1个采样周期内的开关状态。

由式(5)、(10)可知，下一时刻功率由电网电压、变换器交流侧电压电流以及当前时刻功率共同决定。

变换器交流侧电流可通过前向欧拉法用电网电压和变换器交流侧电压表示[19]。因此由式(15)可知，通过改变变换器的开关状态，调节交流侧输出电压，可达到控制功率的目的。

变换器工作时，有8种可能的开关组合，把这8种开关状态组合映射到d、q坐标系，可得到6个相互夹角为60°的非零电压矢量和2个位于坐标原点的零电压矢量，这8个矢量将空间分为6个扇区，如图3所示。

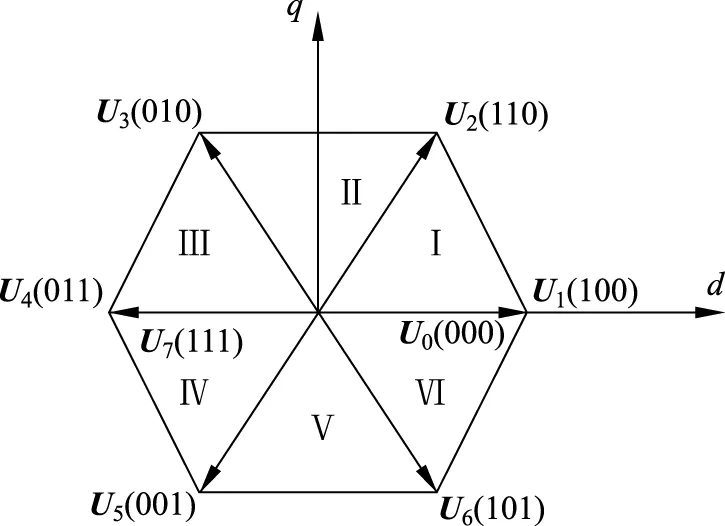
图3 基本电压空间矢量Fig.3 Space vector of basic voltage

为了实现变换器的单位功率因数运行和减小功率脉动，在参考电压矢量选取部分引入一个机器学习中的简单代价函数[20]，即

C= [P*(k+1)-P(k+1)]2+[0-Q(k+1)]2

(16)

首先基于代价函数取最小值选择参考电压矢量，然后判断参考电压矢量所在扇区，选取相邻的2个非零电压矢量及零电压矢量并通过分配各自作用时间等效参考电压矢量，最后依据相邻矢量开关动作变化的次数最小的原则得到相应的开关序列，从而生成PWM脉冲信号[21]。

3 控制系统整体结构框图

SVPWM MP-DPC控制系统整体结构如图4所示。通过模型预测算法计算产生的交流侧参考输出电压，经反帕克及克拉克(IPark & Clarke)坐标变换及SVPWM调制后生成网侧PWM变换器的开关驱动信号，实现了对直流母线电压快速追踪调节和网侧变换器单位功率因数运行的目的。

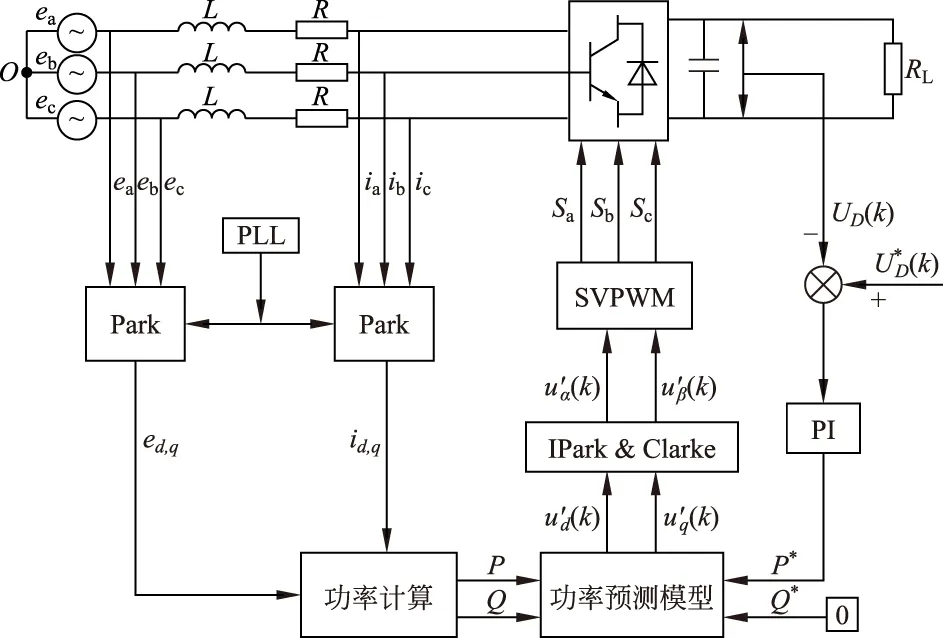
图4 整体控制框图Fig.4 Overall control block diagram

4 仿真结果分析

根据上述提出的SVPWM MP-DPC策略，基于PSCAD/EMTDC软件，搭建了仿真模型对其进行仿真研究。仿真系统主要参数见表1。

表1 仿真主要参数Table 1 Simulation main parameters

图5(a)和5(b)分别给出了FESAS放电模式下传统型DPC和改进型DPC网侧稳态A相电压与电流仿真波形。由图5可知：二者虽然最终都实现了单位功率因数，但传统型DPC在t=0.05 s前电流畸变严重且不稳定，而改进型DPC从仿真开始到结束几乎一直保持稳定且电流纹波较少。

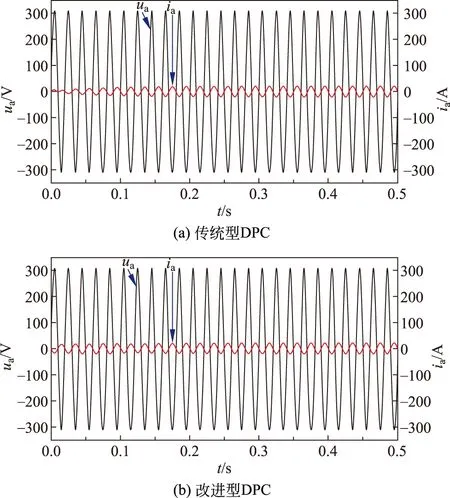
图5 稳态A相电压电流仿真波形Fig.5 Steady state A phase voltage current simulation waveform

图6(a)和6(b)分别给出了2种控制策略下的网侧A相电流FFT分析结果。由图6可知：通过在传统型DPC中引入MPC和SVPWM算法，网侧电流总谐波失真(total harmonic distortion, THD)含量显著减少，从4.109 3%降至3.833 4%，电流质量得到了明显提高，且低频段谐波更少，易于滤波器的设计。

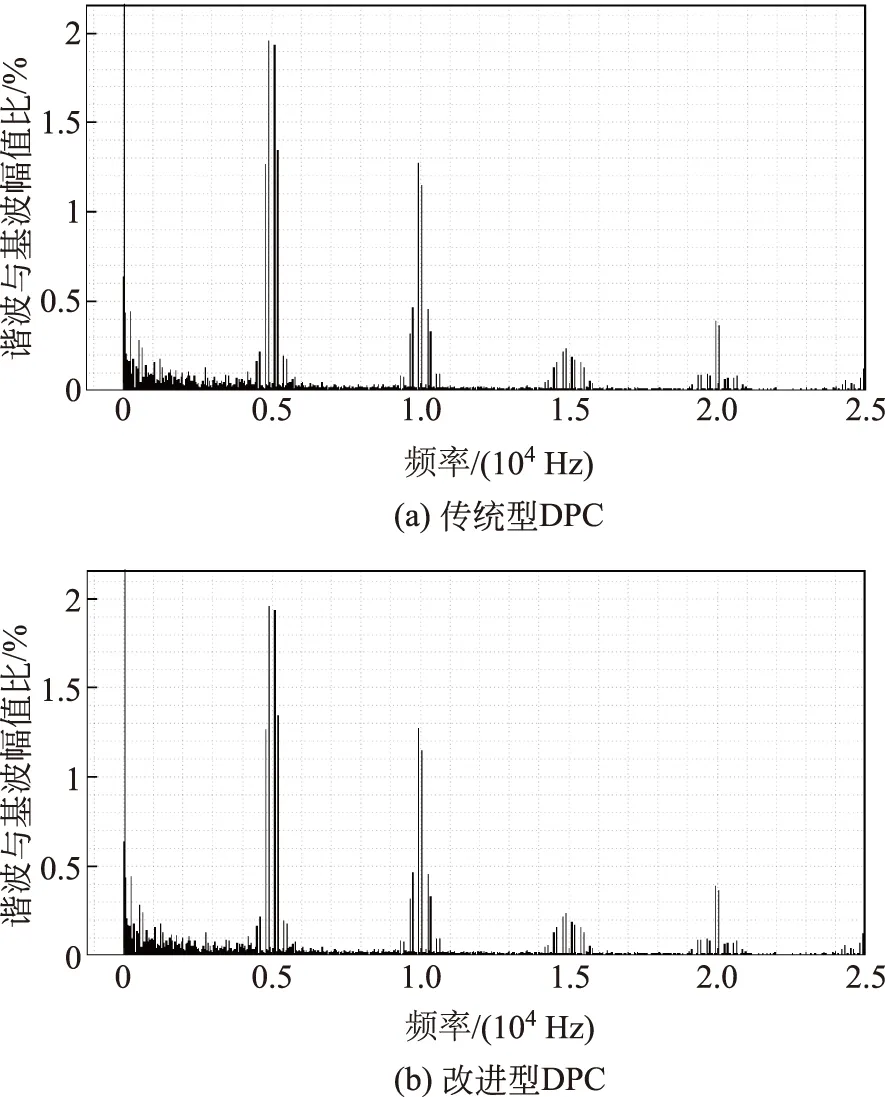
图6 A相电流FFT分析结果Fig.6 A phase current FFT analysis results

图7(a)和图7(b)分别给出了FESAS放电模式下传统型DPC和改进型DPC网侧稳态瞬时功率仿真波形。其中，有功功率参考值为-4 kW，无功功率参考值为0 kV·A。由图7可知，传统型DPC的功率脉动较大，改进型DPC的功率脉动很小。

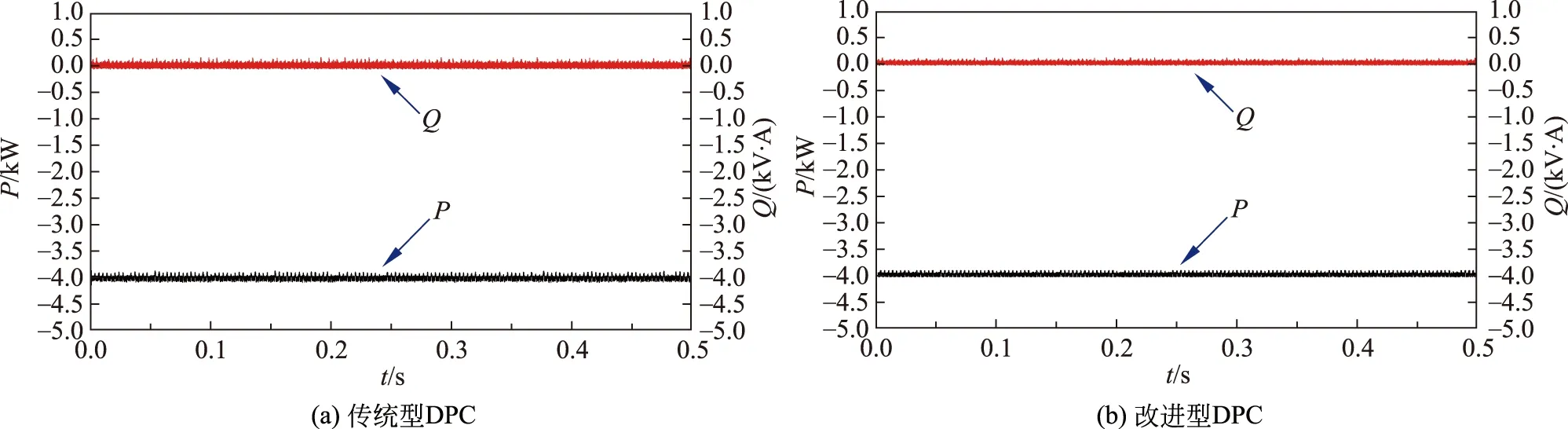
图7 稳态瞬时功率仿真波形Fig.7 Steady state transient power simulation waveform

图8给出了FESAS充电模式下改进型DPC策略的仿真波形。由图8可知：变换器可近似为单位功率因数整流运行，直流母线电压稳定，网侧电流正弦度较高，谐波含量较少，因此验证了该控制策略的可行性。

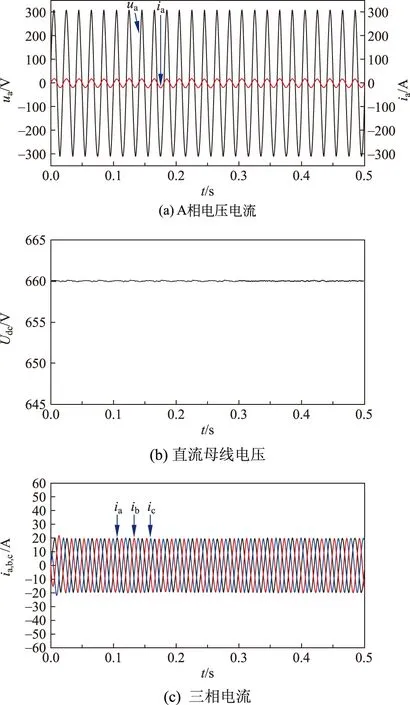
图8 改进型DPC系统仿真波形Fig.8 Improved DPC system simulation waveform

图9、10分别为FESAS充电模式下RL突然增大一倍时，采用传统型DPC和改进型DPC策略下直流母线电压、网侧A相电压电流波形对比图。在t=0.2 s时，负载突变为原来的2倍，相比于传统型DPC策略，采用改进型DPC策略的直流母线电压脉动更小，响应速度也更快，对负载扰动表现出更强的鲁棒性。此外，2种策略的电流动态响应都非常快，速度几乎一样，但改进型DPC策略电流纹波更小，稳态性能更好。

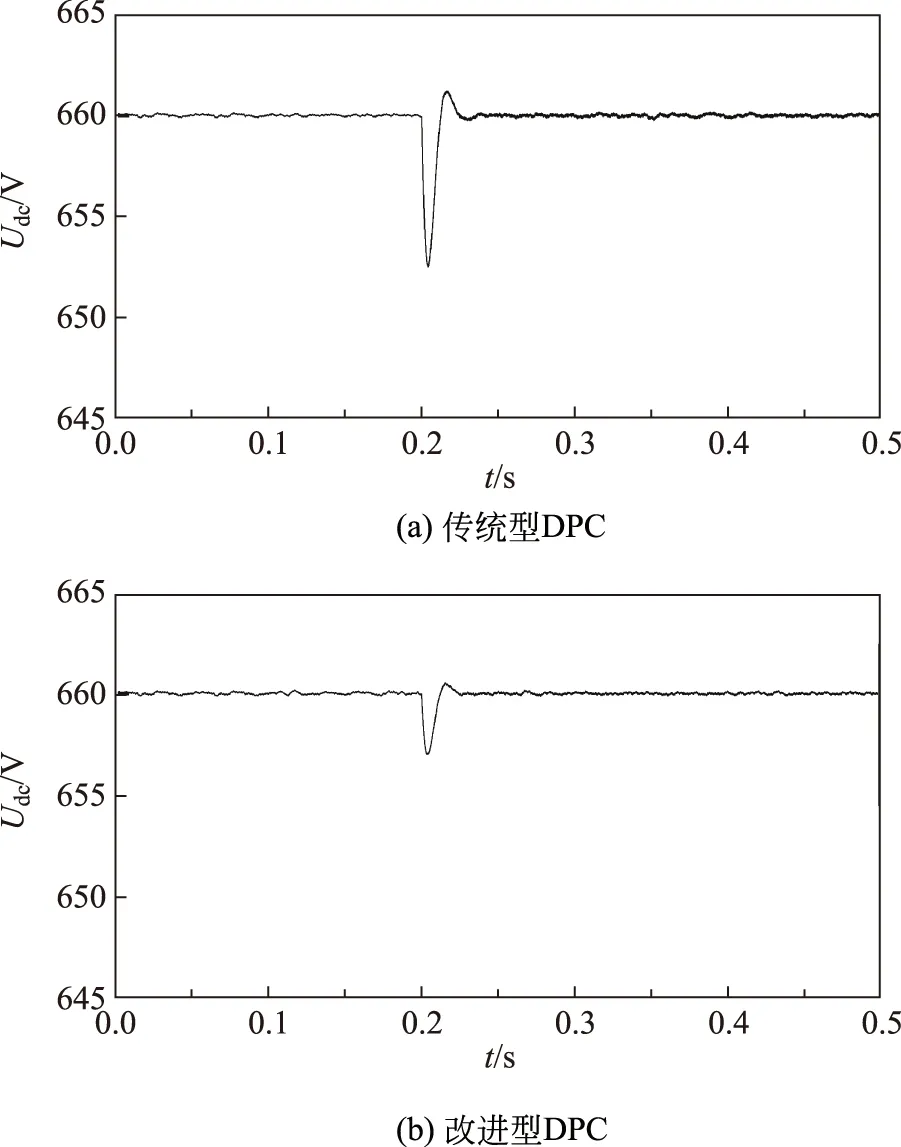
图9 直流母线电压对比图Fig.9 DC bus voltage comparison

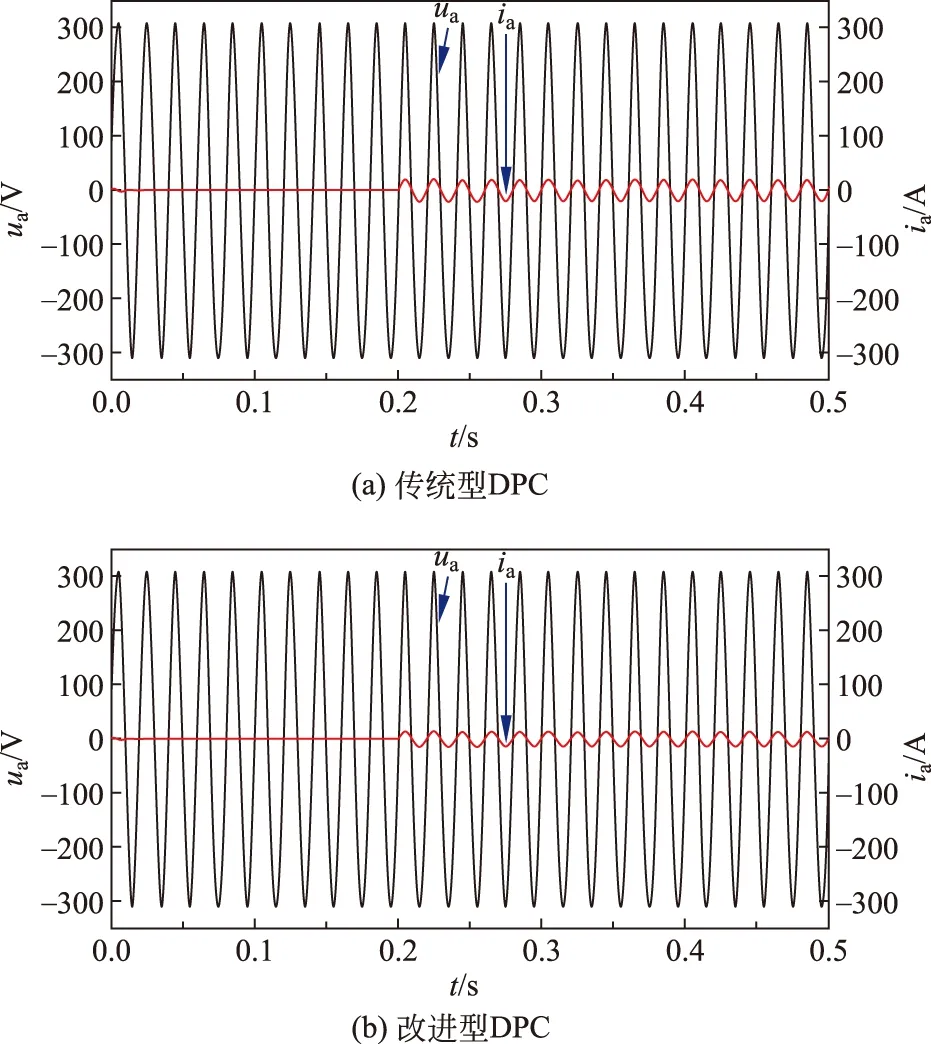
图10 A相电压电流对比图Fig.10 A phase voltage current comparison

5 结论

本文提出的SVPWM MP-DPC策略改进了功率模型、电压外环控制策略和调制方式，使得系统具有良好的动、静态性能。通过PSCAD软件对该控制策略与传统直接功率控制策略进行了对比仿真研究，结果表明，相较于传统型DPC策略，改进型DPC策略系统开关频率固定，网侧谐波含量较少，直流母线电压跟踪性能优越，静态性能良好，同时保留了前者的快速动态响应特性。