空时分组码在PPM 调制下的信道容量

李静

（陕西省建筑职工大学，陕西 西安 710068）

两根发射天线的空时分组码[1]在1998 年由Alamouti SM 研究得出。紧接着，以空时分组码两根发射天线为基础研究了多根发射天线，并且对正交空时分组编码[2]进行了定义。信道容量（Channel Capacity）可以平均最大速率传送信息，其计算方法有多种，通常应用连续信道容量和离散信道容量两类。bit/符号和bit/s 定义为离散信道的基本单位。研究发现，影响信道容量的因素有信噪比、发射天线数、接收天线数、调制数、光强闪烁衰减系数等。无线通信干扰可以转为潜在的通信能力，即每一条独立的信道可由多径线路来充当，不同的信息被同时传送，即加倍地增加了无线光MIMO 的容量，也就是说，多径并行传输多个不同的数据序列。空时编码应用领域广泛，具有很好的发展前景，空时编码体制已经作为第三代移动通信的标准体制，在第四代移动通信系统中也起到了关键作用。

1 信道容量

1.1 平均信息量

按照信息论的概念，统计发送xi和收到yj信息量的平均值，其中，发送xi的不确定程度信息量减去收到yj的不确定程度信息量，可得到C值[3]为：

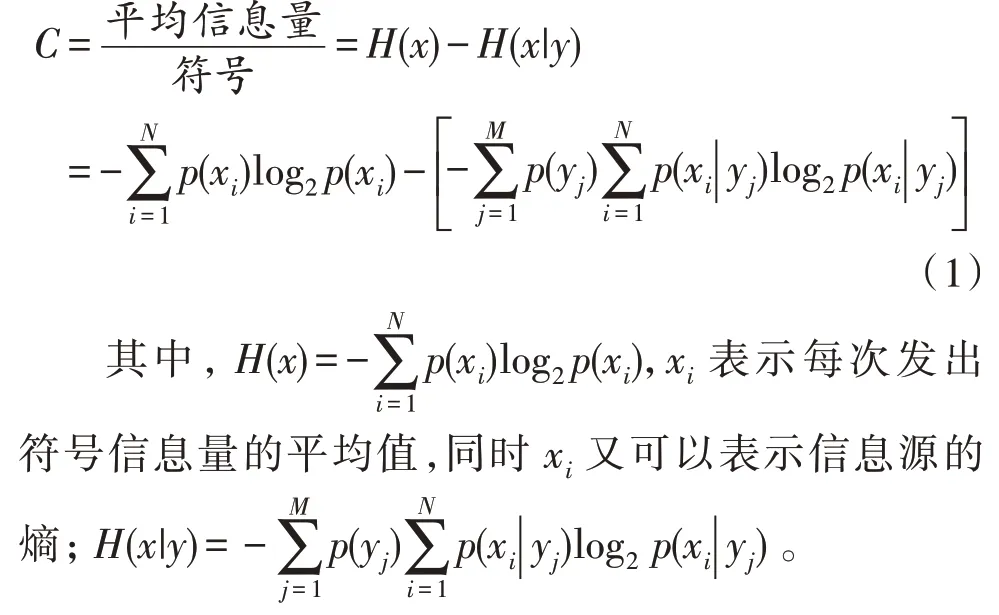
1.2 根据全概率公式、贝叶斯公式得出信道容量公式

p(xi)称为先验概率，定义为发出符号平均信息量xi的概率（i=1，2，…，n）；p(yj)称为后验概率，定义为收到符号平均信息量的概率（j=1，2，…，m）；p(yj|xi)称为转移概率，定义为发出符号平均信息量xi和收到符号平均信息量yj在一定条件下的概率。

根据贝叶斯公式，可得：

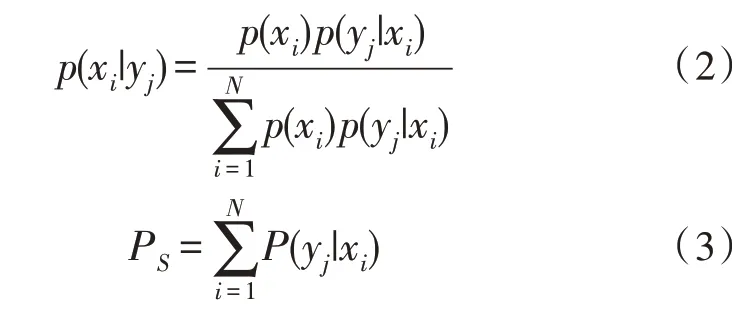
根据全概率公式，可得：

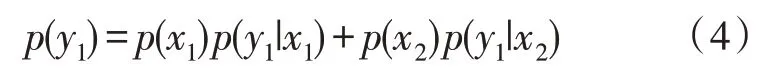
式中，P(y1)表示收到符号y1时的概率，j=1；P(x2)表示发送符号x2的概率，i=2；P(y1|x1)为转移概率，表示发出符号x1在一定条件下收到符号y1的概率；把式（3）、（4）代入式（2）可得p(xi|yj)，最后，代入式（1）中，可以得到信道容量公式。

2 仿真分析和结果

利用蒙特卡罗方法进行仿真试验，仿真的条件为：总发射功率ES不变，ES=1；样本数为100 000，其中，取二进制数据流；光电转换效率η=0.8；试验模型采用大气湍流模型、对数正态分布模型、Gamma-gamma 分布模型下的不同发射天线数和接收天线数目；利用4PPM 调制方法进行调制；闪烁因子SI=0.4 时为弱湍流、SI=0.9 时为中湍流、SI=1.25 时为强湍流。大气结构折射率常数分别为2.10×。距 离L为8 000 m 和1 000 m，波长λ=1.06 μ m。

2.1 α 服从对数正态分布概率密度函数

α服从对数正态分布概率密度函数，如式（5）所示。

式中，μx为平均信息值，为方差，其中μx和满足μx=-，α为光强衰减闪烁系数，A为振动幅度值[4]。

2.2 Gamma-gamma 分布概率密度函数

Gamma-gamma分布概率密度函数如式（6）所示。

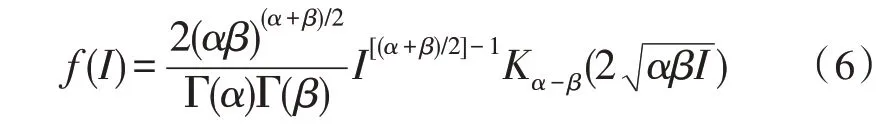
式中，I为接收端的光强，Γ(·) 是gamma 函数，Kα-β(·)是第二类修正贝塞尔函数[5]，α和β定义如下：

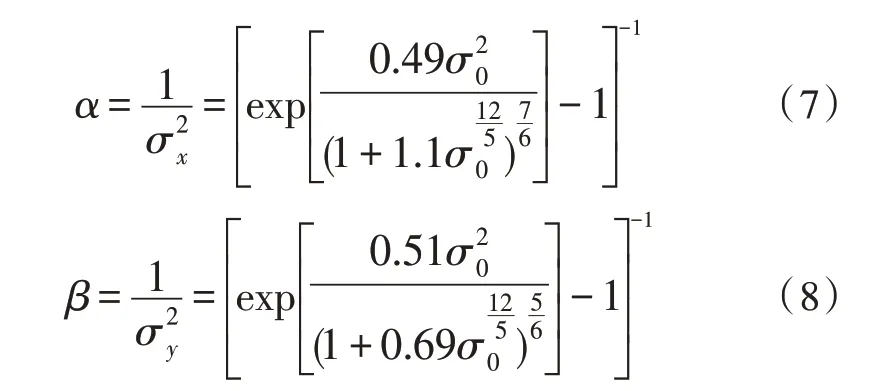
SI为闪烁因子，SI与α和β的关系[6]为SI=1/α+1/β+1/(αβ)。

＜1 为弱湍流；≈1 为中湍流；＞1 为强湍流。

2.3 两种情况下的仿真图像

图1 为SI=0.4 时对数正态分布下的信道容量，Monte Carlo 仿真1×1，2×2，3×3，4×4 系统的信道容量，从发送天线角度来看，当接收天线数目加大时，信道容量明显加大。

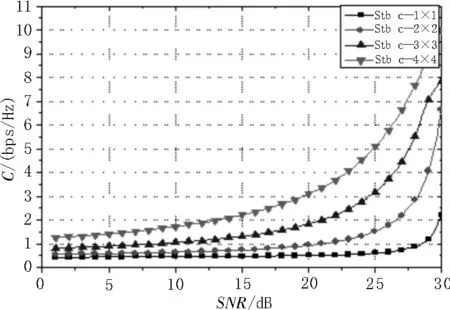
图1 SI=0.4 时对数正态分布下的信道容量

图2 为SI=0.4 时的Gamma-gamma 分布，从仿真图可以得出4×4 的空时分组码系统性能最佳。

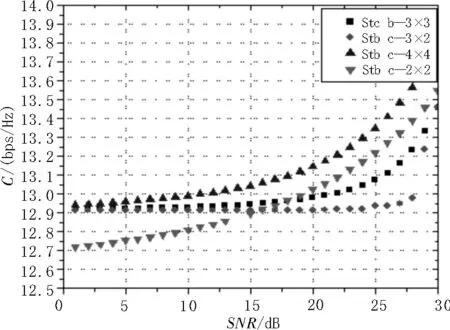
图2 SI=0.4时Gamma-gamma分布下的信道容量

图3 为SI=0.9 时Gamma-gamma 分布下的误码率，Monte Carlo 仿真1×1，1×2，2×1，2×2 系统的误码性能。从仿真图可以得出，2×2 系统的误码率最小，1×1 系统的误码率最大，在PS=10-2时，采用空时分组码后2×2 比2×1 系统性能提高了约10 dB。

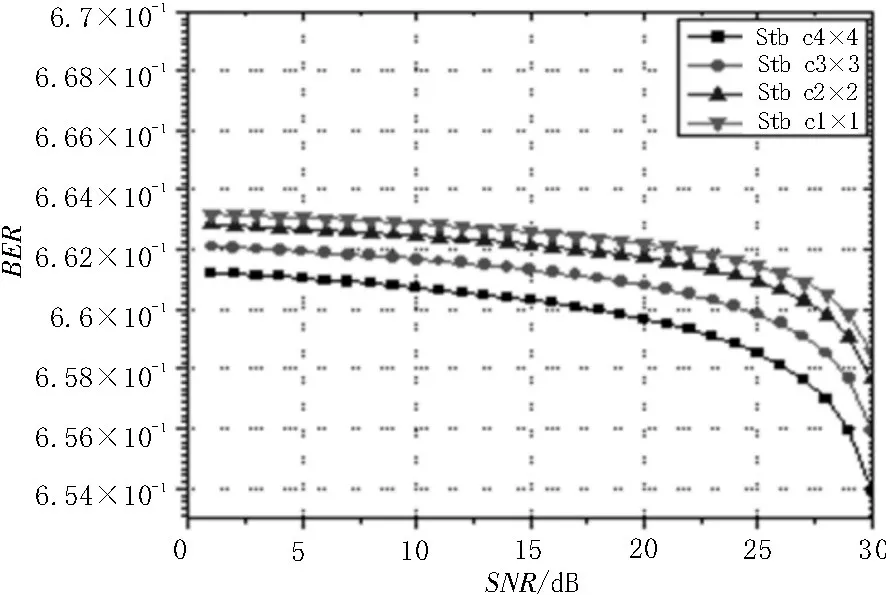
图3 SI=0.9时Gamma-gamma分布下的误码率

图4 为SI=1.25 时Gamma-gamma 分布下的误码率，从仿真图可以看出，在PS=6.6×10-1时,4×4 比1×1 的空时分组码系统性提高了约10 dB。关于对数正态分布和Gamma-gamma 分布下中断概率的研究如图5、6 所示，弱湍流、对数正态分布下的仿真距离L=81 000 m，波长λ=1.06 μm，则大气结构折射率常 数分别为，此时从小到大为0.12、0.32、0.52，中断概率减小信噪比反而增加；在中强湍流信道下，按照Gamma-gamma 仿真对中断概率进行研究。仿真时距离L=8 000 m，波长λ=1.061 μm，大气结构折射率常数分别为由小值逐渐增大时，[α,β]定义为[4,1.6]、[4.3,1.3]、[8,1]，中断概率减小，信噪比不断增大。

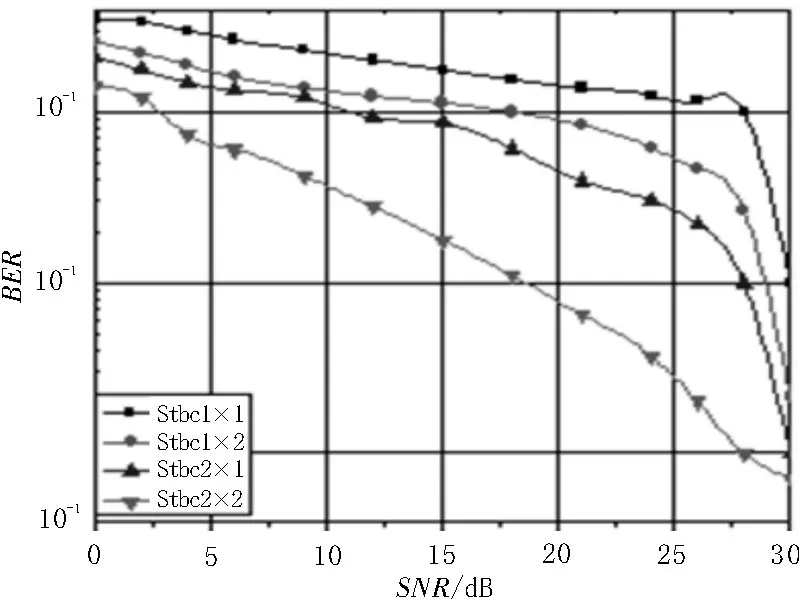
图4 SI=1.25时Gamma-gamma分布下的误码率

图5 PPM调制下对数正态分布的中断概率

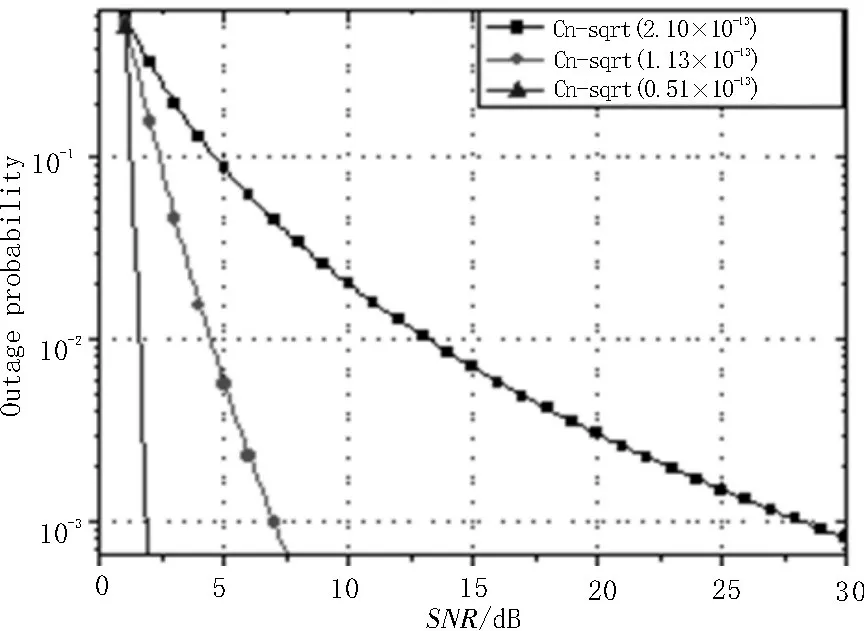
图6 空时分组码在PPM调制下Gamma-gamma分布下的中断概率

3 研究现状分析

Teladar 在1995 年对衰落抑制MIMO 信道容量[7]进行了研究。Foshini 在1996 年给出了多输入多输出分层（D-BLAST）算法[8]，对分层空时编码进行了定义，通过BLAST 实验得到了应用。1998 年TarokhV等人首次提出并定义了STC(空时码）[9-11]。

单根发射天线编码应用推广多根发射天线[12]是Tarokh 等人在Alamouti 方案基本理论上发展的。复信号发射天线数和分集增益达到最大，且它们的和为2，而当时不存在分集增益达到最大和传输速率达到最大时发射天线数为1。同时，文献[13]中提出了准正交或非正交空时分组码。

为了能够获得最大的发射分集增益，利用了STBC 正交设计理论的无时间冗余，采用最大似然译码算法得到最大的发射分集编码增益来降低译码复杂度。空时网格编码的方法是TarokhV 首先提出[14]的。分集增益和编码增益由空时网格编码提出，码元前后发送具有一定的相关性，部分码元发送错误，但是整帧的数据仍正确。空时网格编码在编码过程中的优点：性能较佳、抗衰落能力强、用途广泛等，但还是有一些缺点，比如空时网格编码在编码过程中搜索强的编码比较困难、网格编码在采用维特比译码算法时比较复杂而且计算的效率相对比较低。

4 结论

文中利用先验概率、后验概率、转移概率根据贝叶斯公式、全概率公式得出信道容量C的公式，且得出影响信道容量公式[15]的因素有信噪比、发射天线数、接收天线数、调制数、闪烁因子。

文中主要研究了空时分组码信道容量，以及影响信道容量的中断概率和误码率。通过Monte Carlo 方法进行仿真，从仿真结果得出以下结论：1）在相同的调制方式和编码下，在信道容量好的情况下，其发射天线数多；2）在相同的调制方式和编码下，发送和接收天线数越多，误码率越小；3）大气结构折射率常数一定时，信噪比增加时中断概率却在减小[16-17]。

文中主要按照最基本的信息论的方法推导MIMO 信道容量、中断概率、误码率，采用Matlab 仿真方法分别在对数正态分布模型、Gamma-gamma 分布模型下对不同天线数进行仿真，得出其最优的编码。