变速工况下采煤机行星齿轮传动系统故障诊断
2021-07-30毛清华张勇强赵晓勇张旭辉樊红卫张飞
毛清华, 张勇强, 赵晓勇, 张旭辉, 樊红卫, 张飞
(1.西安科技大学 机械工程学院, 陕西 西安 710054;2.陕西省矿山机电装备智能监测重点实验室, 陕西 西安 710054;3.西安重装智慧矿山工程技术有限公司, 陕西 西安 710000)
0 引言
采煤机是综采工作面核心装备之一,其工作环境恶劣,运行时极易受到煤、矸石等载荷冲击,同时持续遭受水汽、煤尘等腐蚀[1],导致其牵引部行星齿轮传动系统易出现齿轮磨损、点蚀、裂纹等问题[2],轻则影响煤矿生产效率,重则导致设备损坏、生产中断,造成重大经济损失,甚至引发安全事故。因此,对采煤机牵引部行星齿轮传动系统进行故障诊断,对保障采煤机安全运行具有重要意义。
采煤机截割煤层时,因煤层硬度不同,需通过调整牵引速度达到增大截割转矩的目的[3],使得牵引部行星齿轮传动系统处于变速工况,且因行星齿轮传动系统结构复杂,导致振动信号存在多种调制现象[4]。阶次分析是旋转机械振动信号分析及故障诊断的重要技术之一,其特点是能够充分利用转速信息,将变速信号转换为稳速信号[5]。Song Baoyu等[6]采用阶次分析技术提取斜齿轮低速旋转时的故障特征,实现了斜齿轮早期故障特征的准确识别。李静立等[7]针对变速工况下滚动轴承故障振动信号具有多分量调制的特点,将局部均值分解与阶次分析技术相结合,有效应用于变速工况下滚动轴承故障诊断。陈长征等[8]针对风电机组工作环境恶劣和振动信号具有非平稳特性的问题,提出基于阶次分析和小波阈值去噪的故障诊断方法,与FFT(Fast Fourier Transform,快速傅里叶变换)方法相比消除了因转速不稳定引起的频率模糊现象,并通过风场试验验证了该方法的有效性。
本文针对采煤机行星齿轮传动系统变速工况和振动信号调制现象,将阶次分析与包络谱相结合,提出了基于包络阶次谱分析的采煤机行星齿轮传动系统故障诊断方法,可有效提取行星齿轮传动系统的故障特征。
1 包络阶次谱分析原理
1.1 阶次分析
计算阶次跟踪(Computed Order Tracking, COT)[9-10]是目前应用最普遍的阶次分析技术,其在测量轴上安装1个转速计,与振动传感器同时采样信号,以获得同步数据,再根据转速信号计算等角度重采样时间,对原始振动信号在重采样时间进行插值处理,以获得等角度重采样数据,实现阶次跟踪,如图1所示。该方法简化了硬件,通过上位机实现等角度重采样,降低了信号分析成本,且稳定性较强,可保证较高的精确度。
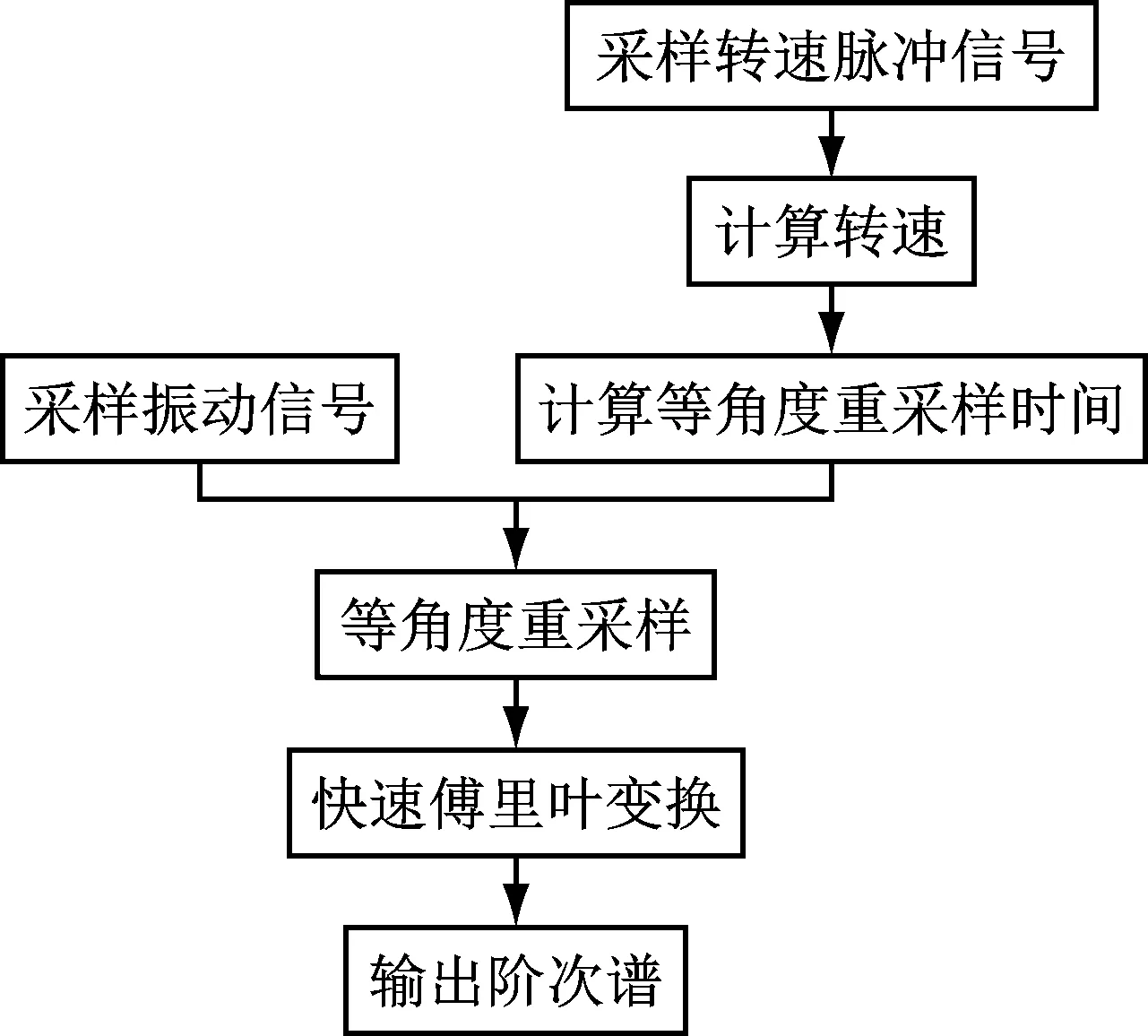
图1 阶次分析流程
阶次定义为参考轴每转内发生的循环振动次数,即
O=60f/n
(1)
式中:O为观测对象的阶次;f为观测对象的振动频率;n为参考轴转速。
观测对象振动频率与参考轴转速之比为恒定值,即设备运行在变速工况时,阶次不会随转速发生改变。
采用阶次分析技术对振动信号进行等角度重采样时,需确定重采样时间。假设设备做匀变速运动,有
(2)
式中:θ(ti)为等角度重采样时间ti对应的转角,i=0,1,2;Δβ为转角增量。
转角θ(t)可用1个一元二次方程表示:
θ(t)=a0+a1t+a2t2
(3)
式中:t为时间;a0,a1,a2为待定系数。
转动相同的转角增量Δβ,通过鉴相装置得到脉冲序列信号,通过相邻2个脉冲间隔时间得到等角度重采样时间的对应转角θ(ti)。t0,t1,t2可直接从脉冲序列信号中提取,将式(2)代入式(3),得到以下矩阵方程:
(4)
求解式(4)可得系数a0,a1,a2:
(5)
根据式(3)可得
(6)
通过离散化进行角域重采样,则转角为
θ(t)=kΔθ
(7)
式中:k为插值系数;Δθ为角度间隔。
根据式(6)、式(7)可得出等间距角位移序列对应的时间序列,即等角度重采样时间序列:
(8)
将式(5)代入式(8)得到整个时间序列后,对原始振动信号进行三次样条插值,得到各个时间节点对应的角域幅值曲线,即角域信号。对其进行频谱分析即可得到信号阶次谱。
阶次分析是将非稳态的时域信号转换为稳态的角域信号。因此行星齿轮传动系统在非稳态下的特征阶次谱与稳态的特征频谱是一一对应的。
1.2 包络阶次谱分析
COT以参考轴的转频为基准阶次1,虽然能将时域变速非平稳信号转换为等角度采样的角域平稳信号[11],但由于角域重采样信号存在调制现象,仅通过阶次分析难以达到理想效果。鉴此,首先对原始振动信号进行Hilbert包络分析,并根据转速信号计算等角度重采样时间序列;然后对振动信号包络进行等角度重采样;最后对重采样的角域信号进行FFT分析,得到其包络阶次谱[12-13]。具体流程如图2所示。

图2 包络阶次谱分析流程
2 仿真分析
为了验证包络阶次谱分析的有效性,进行仿真分析。模拟变速工况下采煤机行星齿轮传动系统存在的调制现象,2个振动仿真信号为
x1(t)=sin 2πt2
(9)
x2(t)=sin 10πt2
(10)
调制仿真信号为
x3(t)=x1(t)x2(t)
(11)
低频信号x1(t)为被调制信号,高频信号x2(t)为载波信号。由式(1)可得x1(t),x2(t)的特征阶次分别为1,5。x1(t),x2(t)波形分别如图3、图4所示,其中g为重力加速度。可看出x1(t),x2(t)频率逐渐增大,通过频谱分析难以辨别信号特征。

(a) 时域

(a) 时域
通过等角度重采样得到的x1(t),x2(t)角域信号及阶次谱分别如图5、图6所示,可看出阶次分析可将变速信号转换为等角度的角域信号,x1(t),x2(t)特征阶次分别为1,5,与理论阶次一致,表明阶次分析可以有效提取变速非平稳信号特征。
(a) 角域信号
(a) 角域信号
调制信号x3(t)波形如图7所示。可看出x3(t)频率逐渐增大,通过频谱分析难以辨别信号特征。x3(t)阶次谱如图8所示,可看出信号经调制后,通过阶次分析得出的特征阶次为4,6,与理论阶次1,5不符。采用包络阶次谱分析得到的x3(t)包络阶次谱如图9所示,可看出特征阶次为1,5,与理论阶次一致,表明本文方法可有效提取变速调制信号的阶次特征。

(a) 时域

图8 x3(t)阶次谱

图9 x3(t)包络阶次谱
3 试验验证
采用动力传动故障诊断综合试验台(图10)的行星齿轮传动系统模拟变速工况下采煤机牵引部行星齿轮传动系统进行故障特征提取试验。该试验台行星齿轮传动系统中的二级太阳轮存在裂纹故障,通过上位机设置电动机转速为0~1 800 r/min,转矩为5 N·m。在第二级行星齿轮传动系统的径向安装加速度传感器,其灵敏度为103 mV/g,信号采样频率为10.24 kHz。

图10 动力传动故障诊断综合试验台
试验台两级行星齿轮传动系统的主要零件转动频率和啮合频率见表1。二级太阳轮裂纹故障特征频率为15.6 Hz。

表1 试验台行星齿轮传动系统主要频率
以电动机输出轴为参考轴,其阶次为1。根据式(1)计算得二级太阳轮裂纹故障的阶次为0.52,一级行星齿轮传动系统的啮合阶次为3.64,二级行星齿轮传动系统的啮合阶次为16.67。变速工况下二级太阳轮出现裂纹故障时振动信号波形如图11所示,电动机端转速脉冲信号如图12所示。根据图11(a)和图12可知,随着电动机转速增大,振动信号幅值增大;根据图11(b)可知二级太阳轮裂纹故障状态下振动信号频谱范围较宽,存在较强的频率混叠现象,没有出现某一固定频率及其倍频成分,因此难以采用频谱分析对变速工况下振动信号进行特征提取。

(a) 时域
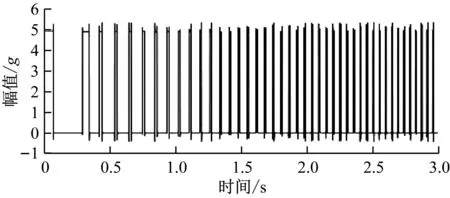
图12 电动机端转速脉冲信号
振动信号阶次谱如图13所示,可看出阶次谱中存在以故障特征阶次的倍频为间隔的调制边带。采用包络阶次谱分析方法得到的包络阶次谱如图14所示,可看出突出阶次为0.494 0,0.975 9,3.494 0,16.660 0,与二级太阳轮裂纹故障阶次0.52、电动机输出轴阶次1、一级行星齿轮传动系统啮合阶次3.64、二级行星齿轮传动系统啮合阶次16.67基本相符,即能够诊断出二级太阳轮发生故障,与实际情况一致。

图13 振动信号阶次谱

图14 振动信号包络阶次谱
4 结语
针对采煤机牵引部行星齿轮传动系统变速工况下的故障诊断问题,提出了一种基于包络阶次谱分析的故障诊断方法。仿真和试验结果表明:阶次分析可有效提取变速工况下不存在调制现象的振动信号特征阶次,而不能有效提取变速工况下调制信号的特征阶次;包络阶次谱分析可有效提取变速工况下调制信号的特征阶次,为变速工况下采煤机牵引部行星齿轮传动系统故障诊断提供了新的途径。
