基于PCSiWaPro软件的土坝和堤坝的稳定性模拟
2021-07-30毛玉芳唐斌斌杭天飞
毛玉芳,唐斌斌,赵 俊,杭天飞,王 盼
(1.宜兴市新庄街道水利站,江苏 宜兴 214200; 2.扬州市勘测设计研究院有限公司,江苏 扬州 225000)
大坝和堤防为防洪的防护结构,堤坝边坡稳定性问题是岩土工程和水利工程中最常遇到的问题之一。影响边坡稳定性的因素很多,其中植被是决定性因素之一。植被对边坡稳定性的显著影响主要有两个方面,通过土壤-植物-大气连续体(SPAC)的水分运动和根系对土壤进行加固。植被是SPAC的主要组成部分,负责水的吸力对抗重力。植物通过吸收部分土壤水分,在斜坡的干燥过程中起着重要的作用。这些被吸收的土壤水分随后将通过蒸腾作用被排到大气中。最终,这种水循环系统将导致更干燥和更稳定的斜坡。近年来,国内外学者对该领域进行了大量的研究,并发展出较为实用的分析边坡稳定性的数值方法。典型的方法有无限斜率方程法、普通切片法、毕肖普简化法、Janbu简化法、Spencer法[1-3]。而无限大边坡方程中含水量与边坡稳定性关系密切,能较好与非饱和坝体水流模拟相结合。PCSiWaPro®软件能基于二维空间上用有限元方法求解理查兹方程,模拟瞬态边界条件下的水饱和度分布,确定上述的影响因素对贯流式和地质不稳定部分饱和地区的土坝的渗流线为边界完全饱和与坝体部分饱和区。
本文利用PCSiWaPro®软件,建立一个包含几何形状、土壤特性、气候参数、土工水力和时变边界条件等信息的大坝二维模型,计算坝体中的水饱和度及大坝空气侧的流量;在模型中设置一个观测点,将渗透线深度的实测值与模拟值进行比较,用于评估天然或人造斜坡的稳定性。
1 工程概况
本文以宜兴市洑西河油车水库堤坝作为研究对象,该水库为中型水库,集水面积41.54 km2,总库容3 324×104m3。2018年,该水库受强降雨、高水位影响,遭遇了50~100年一遇的洪水威胁。该地区暴雨常发地段,受山洪袭击,尤其是在太湖高水位顶托时,河道宣泄不畅,使河道水位雍高,每遇较大降雨,都会使下游城镇、工矿企业和农田受淹成灾,损失严重。水库堤坝具有保护河道沿线人民生活和工农业生产的防洪安全任务,研究该水库堤坝稳定性,对提高水库坝下河道两岸的防洪安全度、增强两岸低洼易涝地区的排涝能力具有积极意义。见图1。
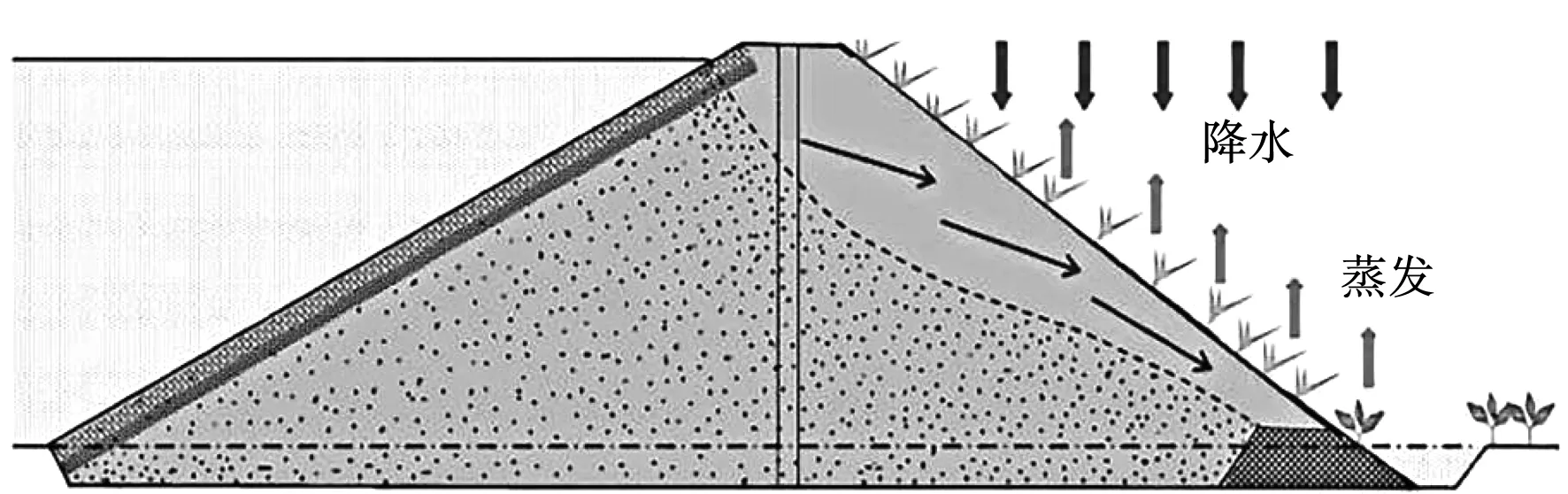
图1 堤坝横断面图
2 基本原理
2.1 无限边坡模型理论
无限边坡模型是最古老和最简单的边坡稳定方法,它假定坝体的任何垂直截面上都存在相同的条件,但该模型无法模拟任何滑坡变异性。无限边坡方程通常是在均质或平均土质的假设下实现的,在这种假设下,边坡的地基总是发生地质力学破坏。分析的目的是以常规安全系数(FS)的形式估计无限边坡破坏的概率[4],无限边坡方程的坡截面见图2。

图2 无限边坡方程的坡截面
均质土的无限边坡安全系数(FS)方程,定义为饱和与非饱和条件下一维无限边坡的抗剪强度与剪应力的比值,公式如下:
(1)

2.2 无限斜率方程
坝体含水量重要相关因素为水深。通过野外测量或非饱和土区模拟,如孔隙水压力和残余体积含水量,可以获得更多的信息。无限斜率方程包含两部分,土体吸力应力特征曲线σs,低于地面以下垂直深度z的函数安全系数FS,公式如下:
(2)
式中:σ为通常由土体自重提供的总应力;uw为孔隙水压力;uα为孔隙气压,θ为体积含水量,θr为残余体积含水量;θs为饱和体积含水量;Se取值为饱和度。θ为瞬态数据收集土壤含水量和土壤吸力(ua-uw)收集的数据用于计算吸应力。
(3)
式中:φ′为内摩擦角;c′为内聚系数;β为坡角;γ为单位重量取决于土壤含水量。
2.3 PCSiWaPro®仿真软件的理论背景
PCSiWaPro®模拟水的流动和污染物在变饱和土壤中的迁移过程,在静止和瞬态边界条件下,流动模型理论采用理查兹方程来计算[5]。这种强非线性偏微分方程计算结果具有滞后效应,特别是含水饱和度与压头之间的关系,在PCSiWaPro®软件中用VAN-GENUCHTEN-LUCKNER方程实现该关系。使用数值有限元方法在两个垂直平面维度上求解瞬态边界条件下的理查兹方程。对于由理查兹方程离散化而产生的线性方程组,采用一种迭代的预条件共轭梯度求解器。理查兹方程和VAN-GENUCHTEN-LUCKNER方程如下:
(4)

(5)
式中:φ为介质(土壤)的孔隙度;hc为湿润相(水)与非湿润相(空气)之间的压头差;α为比例因子;n为斜率,由VAN-GENUCHTEN方程经验参数确定。
3 模型建立与参数确定
3.1 模型建立
PCSiWaPro®软件模拟的模型原型,采用德国德累斯顿大学的水利工程和应用流体力学研究所建立的一个物理大坝模型。该模型堤基宽3.38 m,坡角1∶2,高77 cm。在堤防中采用橡胶墙,橡胶墙可容纳堤防高度的100%(预埋)。在河岸下方,在空气和水边,增加一个基础护堤,高度为30 cm,并允许流入的水和地下水之间的交换。在空气侧坡上建立排水系统,有效地驱散多余的水分。
为求解偏微分理查兹方程,在软件中定义初始条件和边界条件,以整个模型区的压头分布或含水率分布作为初始条件,以时间变化的大坝水边测量的水位作为第一类边界条件,在坝的空气侧定义了一个渗流面,只有当土达到饱和时才允许出水作为第二类边界条件。这样才能更好地表示含水量的变化渗流线上方的非饱和区,使模拟和测量值进行比较。
3.2 参数确定
假设大坝表层覆有防渗层的覆盖砖、砾石和土工织物,没有降水流入大坝,利用具有不同内部岩土结构特征的物理大坝模型进行了多次试验,对模型区域进行离散化,便于表示渗流线上方的非饱和区含水量的变化。同时设置情景分析,估计土壤-水力特性和VAN-GENUCHTEN的参数敏感性。图3给出了水力材料参数α对坝基含水量的影响。

图3 水力材料参数α的灵敏度
由图3可知,坝体内水位变化不大,但与渗流线以上部分饱和区有显著差异,材料参数左边显示比右边更细。这一区域由于黏性较强材料的毛细特性增加而扩大,毛细上升的水更大,这对大坝的空气侧稳定性有负面影响。
4 结果与分析
为模拟大坝计算水位,将坝体、坝下压实土壤、坝区外未扰动土壤的相关参数输入PCSiWaPro®软件,并将水库堤坝的水位测量数据实测值与模拟值进行比较,见图4。在渗透线以上的部分饱和区(深色),也可以检测到滑坡现象。
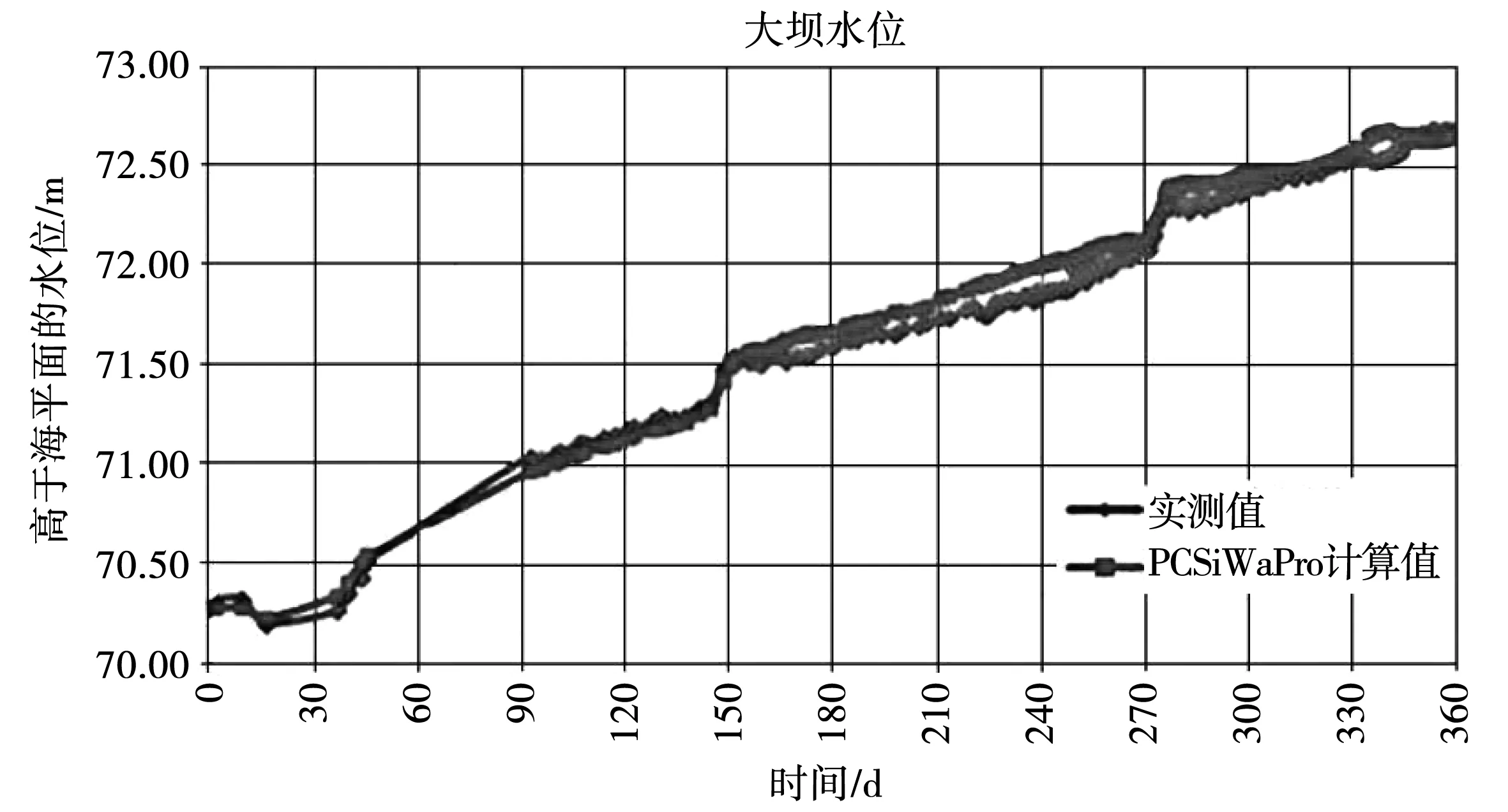
图4 大坝实测水位与计算水位
利用PCSiWaPro®软件,考虑大气条件下750 min后坝体含水量分布,模拟具有大气边界条件的典型负荷情况。图形仿真结果见图5。
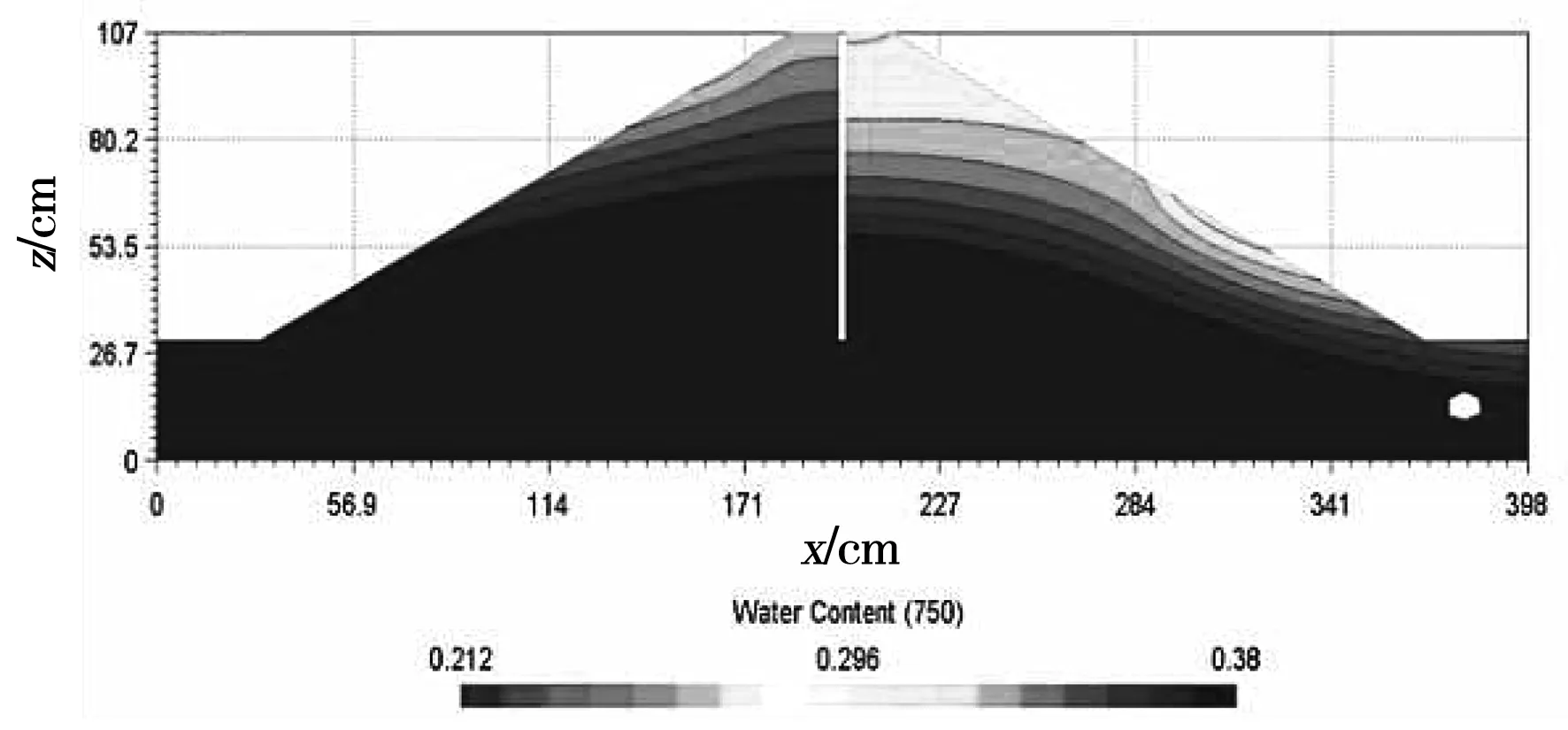
图5 考虑大气条件下750 min后坝体含水量分布
由图5可知,随着排水区含水量的减少,坝基非饱和区含水量增加,气侧存在滑移危险。降水导致额外的水流进入堤坝,从而增加了堤坝的含水量。
5 结 论
通过PCSiWaPro®软件对土坝或堤坝的稳定性进行分析,得出以下结论:①大坝的水位测量数据实测值与模拟值一致性较好,偏差可能是由于估算不准确的水力土壤参数造成的;②大坝物理模型的模拟结果表明,在坝体高度局部饱和的情况下,坝体空气侧的流速可能已经出现,从而影响坝体的稳定性,并可能因土料漂浮而导致滑坡;③研究显示,PCSiWaPro®模型具有在连续规模下模拟长时间的能力。特别是在洪水期间,对坝基含水量的连续监测是判断坝基稳定性的一个很好的指标。这是由于地质力学不稳定已经发生在部分饱和的土壤区域。此外,大坝、堤坝空气侧的植被以及植物根系对大坝稳定性的吸收也有显著影响。依据分析结果,利用PCSiWaPro®软件对大坝水位模拟的仿真结果较好,为评估天然或人造斜坡的稳定性提供了理论参考。
