基于力学-热学-水文地质耦合的堤防稳定性数值模拟
2021-07-30乔磊,赵璇
乔 磊,赵 璇
(德州市水利局 丁东水库运行维护中心,山东 德州 253000)
1 概 述
山东省德州市的丁东水库沿线布设了防洪堤,防洪堤是保护地区免受洪水侵袭的一种常用方法[1]。这种堤防是比较通用的一种岩土结构,但有的堤防较为薄弱,对人民的生活和财产而言存在一定危险,所以监测堤防稳定性也成为当下重点关注的项目[2-3]。如今,研究人员正在寻找一种通用有效的方法来监测堤防稳定性,并预测其破坏的时间和地点[4-5]。许多项目尝试使用热测量,即用光纤特性来测量堤防温度或其他仪器来测量、估计堤防中流体的流量。ISMOP项目是基于温度和孔隙压力传感器建立的一个复杂又危险的预测系统。在实际测量之前,先对水库内水位变化过程中发生的反应进行数值模拟,并得出相应结果,同时为了检验洪水波对堤防稳定性的影响程度需要耦合数值模型。
2 工程概况
丁东水库位于山东省德州市陵城区丁庄乡境内,西北距德州市25.0 km,是一座中型围坝引水式平原水库,属于黄河中下游冲击平原河间洼地。岩性中上部为沙壤土夹裂隙黏土,下部为极细砂、细砂层。坝基地层岩性为第四系全新统冲积层,坝基地层岩性为第四系全新统冲击堆积层(a1Q4),夹湖积堆薄层(1Q4),自上而下分为五大层,10个亚层。堤顶公路为沥青混凝土路,围坝部分全长11 636 m,净宽6 m,隔坝部分全长1 400 m,净宽8.0 m,面层铺设厚度为3 cm。现根据大坝由西至东方向的横截面构建模型,模型见图1。
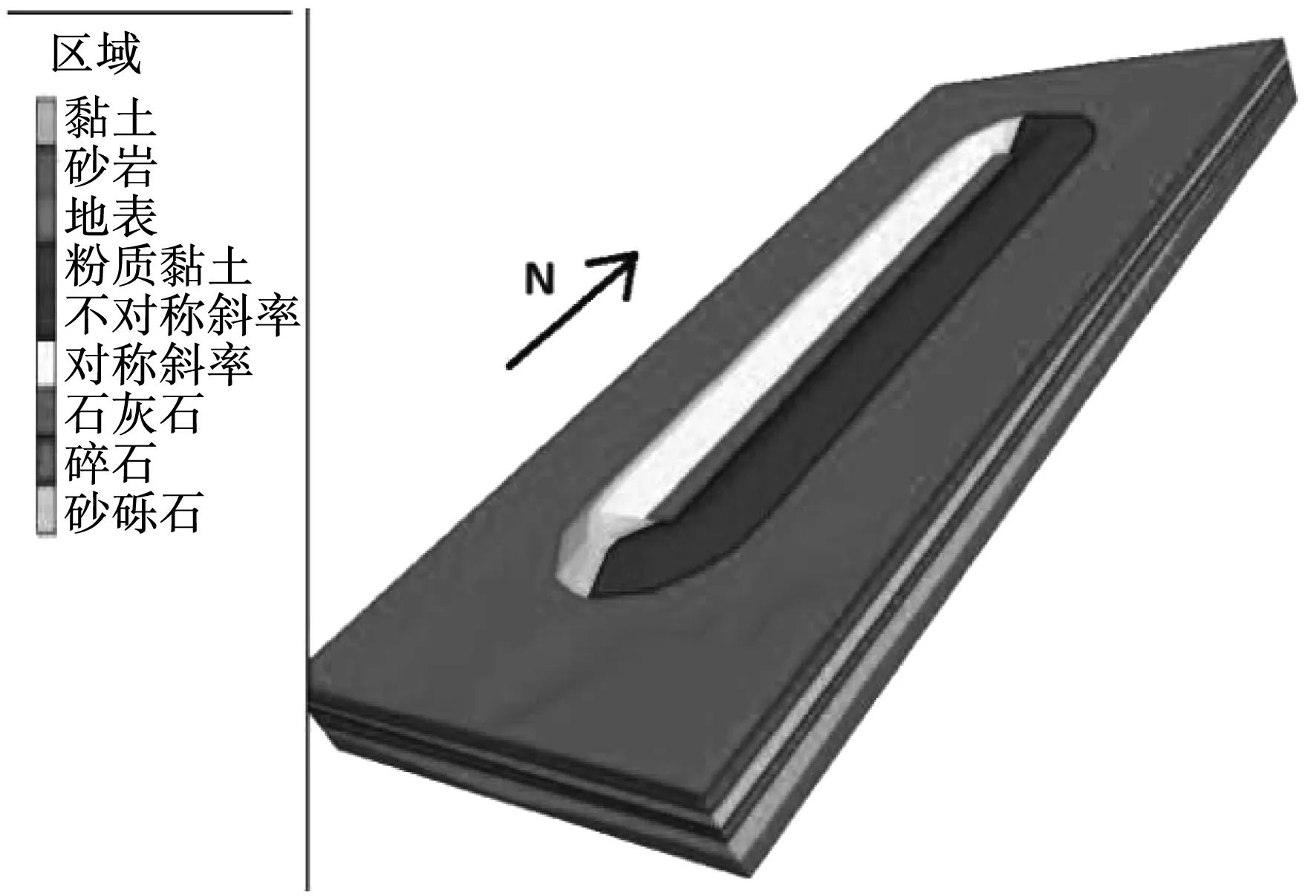
图1 堤坝地质模型
3 数值模拟
本文采用Itasca Flac 2D 7.0软件进行数值模拟。该软件使用有限差分法求解岩土工程问题。
3.1 理论背景
用达西公式表示地下水-力学耦合流体的运输:
qw=-K∇(P-ρwg·x)
(1)
式中:K为流体流动系数(或渗透率);ρw为流体密度;g为重力。
该方程中的流体密度与温度变化相关,可表示为如下形式:
ρw=ρ0[1-βf(T-T0)]
(2)
式中:T0为参考温度;βf为流体体积的热膨胀。
渗透率K与水力传导率kH的关系为:
(3)
当流体流过多孔介质时,有3个力作用在固体基质上,即固体重量、浮力和阻力或渗透力。模拟中都考虑了这些力。
用傅里叶公式描述Flac中的热传递:
qT=-kT∇T
(4)
其中,有效导热系数kT是由两部分构成,分别为流体kwT导热系数和固体ksT导热系数,可由下式表示:
kT=ksT+nSkwT
(5)
在Flac中,热量通过以下两个过程在多孔介质中传递:当热量由流体运动引起时,存在强制对流;当流体运动由温度变化造成的密度差引起时,存在自由对流。
Flac中,用于对流-扩散传热的能量平衡方程如下:

(6)
式中:T为温度;qT为热通量;qw为特定流体的流量;qvT为体积热源强度;ρ0为流体的参考密度;cw为流体的比热容;cT为有效比热容。
cT可定义为如下形式:
cT=ρdCv+nSρ0cw
(7)
式中:ρd和Cv分别为固体物质的体积密度和体积比热容;n为孔隙度;S为饱和度。
3.2 数值模拟
数值模拟建立924×70的方形网格,尺寸为0.1 m。建立的模型深度比地形低2.5 m,为了避免边界效应,偏移量为20 m(从模型边缘到堤岸的距离)。垂直位移固定在模型底部的边缘处,水平位移固定在模型的左右边缘处。用于计算的材料参数见表1。

表1 建模中使用的力学、热学和水文地质特性
再根据以下4个步骤进行建模:①仅计算地质(无堤防)的力;②计算地质和堤防的力;③1 h计算步骤:首先进行流体传递,然后传送热量,最后使水力机械平衡。每一步完成之后,水位和气温的值将随之变化;④安全系数的计算。
图2为根据上述内容建立的带有测量点的2D模型。这些点的位置与坝内温度和孔隙压力传感器的实际位置较接近。点A-D在高于地形0.4 m的地方,两边距离堤防交界点1 m左右。

图2 模拟中的2D模型
4 结果分析
对不同的波浪参数进行17次数值模拟:一次模拟的是平均波浪参数,其余16次模拟只有一个参数发生变化,将各工况列于表2:水位增加对应的测试时间是从0到3.5 m;高水位3.5 m时对应的测试时间;水位下降对应的测试时间是从3.5到0.1 m;低水位0.1 m时对应的测试时间。

表2 数值模拟中波浪阶段的时间 /h
安全系数(FoS)是在每个阶段的波浪结束时进行计算,此参数用于评估洪水过程中堤防的稳定性。当初始土壤温度为8℃、蓄水池内的水温固定在11.04℃时,空气温度见图3,水位变化见图4。

图3 气温和平均波浪在点A-D模拟的温度

图4 平均波浪参数模型的水位和位移长度
分析温度可知,在点B和点C处先开始温度变化,因为点B和点C离水库较近,传感器在点A和点D的反应不如点B和点C明显。
由图5可知,任意时间段,热反应都滞后于孔隙压力传感器的反应,这是因为防洪堤在温度较低的情况下,在入渗过程中发生了冷却作用。在波浪的第一阶段,1 h内垂直和水平方向的位移增加。达到高水位(3.5 m)后,点B和点C的位移开始减少,点A和点D位移继续增加,因为点A和点D距水库较点B和点C更远。当水位下降时,所有点的增加速度都下降。但在低水位(0.1 m)时仍有一些位移,主要是由于堤内水流运动形成的。

图5 基于平均波浪和水位的点A-D的孔隙压力
图6至图9显示了1 h内每阶段的位移、孔隙压力和温度都具有平均波浪。由图6-图9中可以清楚地看到孔隙压力异常,即孔隙含水饱和度不为零,与温度变化或位移变化的区域不对应。
图6所示为第一阶段,水位增加至3.5 m后。不对称(右)堤防和水库底部位移值最大,水库底部附近的孔隙压力在减少,与空气或水接触的区域温度在升高。
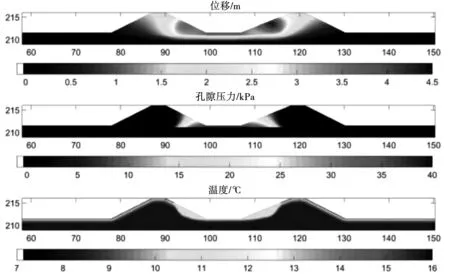
图6 水位上升结束48 h后的位移、孔隙压力和温度
图7所示为水库高水位阶段之后。孔隙压力等值线几乎为椭圆形;最大水流在不透水层上;最大位移在水库底部、也在右边堤防的顶部;温度变化小于水的渗透范围。

图7 高水位结束108 h后的位移、孔隙压力和温度
图8所示的水位下降之后,降低了位移和孔隙压力的值,只有温度超过8℃以上的区域才会增大,这些变化是由空气-土壤对流和水渗透而造成的。这个结论对于最后一个阶段,即图9所示的低水位而言也是正确的,位移接近于零,因此水越过防洪堤顶部的堤防层。

图8 水位停止下降192 h后的位移、孔隙压力和温度
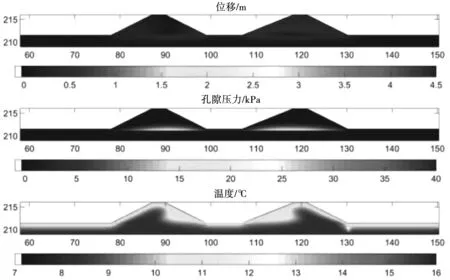
图9 数值模拟结束270 h后的位移、孔隙压力和温度
在所有数值模拟中,安全系数都是在每个阶段结束时计算。不同波形的安全系数见表3,不同波浪阶段的时间见表2,FoS的值按每个阶段最短到最长的时间顺序算出。对于所有测试过的模型,堤坝是稳定的(FoS>1);当水库出水速度最快时,FoS值最低,这个阶段使堤坝稳定性从3.5降低到3.0。

表3 不同波形的安全系数
第一阶段,增加水位时的持续时间对试验结束后的FoS值(变化范围为3.181到3.193)几乎没有影响。高水位(从3.14到3.25)和低水位(从3.09到3.26)的最终FoS值差异最大,长时间的低水位使堤防稳定状态更接近试验前的状态。
5 结 论
根据本文研究内容,结论可分为以下两个方面:
数值模拟结果表明,可以同时计算热力场和水力场的数值,可以用热传感器代替昂贵的孔隙压力传感器,但传感器需放置在不受温度变化影响的位置。此外,热传感器对入渗水的反应要慢于孔隙压力传感器,是因为入渗过程中土壤和水之间发生了能量转换。
稳定性分析结果表明,水位下降,堤防的稳定性随之降低,安全系数从3.5降低至3.0。对所有测试过的洪水波参数来说,堤防是非常稳定的,任一阶段的FoS差异都不大,均小于5%。
