基于非线型滑动面假设的盾构隧道松动土压力计算模型研究
2021-07-30袁大军金大龙郑爱元孙庆文
王 将,袁大军,金大龙,郑爱元,孙庆文
(1.北京交通大学 城市地下工程教育部重点实验室, 北京 100044;2.北京交通大学 土木建筑工程学院, 北京 100044;3.深圳市地铁集团有限公司,广东 深圳 518026;4.济南轨道交通集团有限公司,山东 济南 250014)
土拱效应下盾构隧道的松动土压力的预测对于盾构隧道的合理设计与安全施工是至关重要的。关于土拱效应的理论与实验研究较多,Terzaghi[1]基于Trapdoor实验和极限状态分析所提出的松动土压力计算方法应用最为广泛。Terzaghi认为松动土体的滑动破坏界面上存在一定的剪切力阻碍下沉,将土拱效应解释为松动土与周围土体应力传递,在此基础上,建立极限状态力学模型,很多学者在此基础上深入研究了土拱效应[2-11]。
很多研究是建立在竖直线型滑动面假设基础上的,在该假设下松动土压力的计算模型建立与公式推导相对简单。Terzaghi[1]认为隧道拱顶松动区两侧的滑动边界为竖直线型边界,在该假设下推导得出隧道结构的松动土压力计算公式;Handy[2]考虑主应力轴旋转,认为拱迹线为小主应力的轨迹,并取拱迹线为悬链线型,推导了侧压力系数的计算公式;Kingsley[3]将拱迹线简化为圆弧型,修正了Handy所提出的侧压力系数计算公式;陈若曦等[4]考虑主应力轴旋转效应,基于大主应力拱迹线假设修正了太沙基松动土压力计算方法;蔺港等[5]基于主应力轴旋转理论,建立了考虑基质吸力的松动土压力分析模型;宋锦虎等[6]根据实验结果修正了静水压力下盾构开挖面区域内的侧压力系数,将其用于开挖面前方的土拱计算模型;黎春林[7]认为主应力偏转角度与隧道拱顶位移相关,提出了考虑盾构隧道施工工艺的松动土压力计算方法。
学者们也对滑动面形状做出其他假设,修正松动土压力的计算模型。Shukla等[8]提出了斜直线型滑动面的假设,推导了松动区竖向应力的表达式;吕华伟等[9]根据主应力轴旋转理论得出了斜直线型滑动面的倾角取值方法。陈国舟等[10]和李瑞林等[11]将滑动破坏面形状假设为抛物线,进一步修正了松动土压力计算方法。斜直线与抛物线型滑动面假设虽一定程度上提高了计算精度,但这两种形状假设均缺少相应的实验与理论支撑。另外,目前的松动土压力计算模型中,滑动面剪切力的计算多是基于相关流动法则,而大量试验表面,岩土材料并不服从关联流动法则。
针对上述情况,本文引入滑移线场理论,考虑非关联流动法则,对盾构隧道的松动区滑动面公式进行理论推导,基于本文的滑动面假设并考虑主应力轴旋转效应,求解了松动区边界的侧压力系数,在此基础上得出了盾构隧道的松动土压力计算模型。
1 盾构隧道松动区滑动面形状的讨论
Terzaghi根据Trapdoor试验结果,建立极限状态力学模型,根据单元土条的竖向力平衡推导得出活门之上的竖向应力表达式为
(1)
式中:γ为土的容重;φ为土体内摩擦角;c为土体黏聚力;B为松动区宽度;P0为地表荷载;K为侧压力系数。
将该理论应用于圆形隧道松动土压力求解时,Terzaghi[1]认为隧道拱顶松动区的滑动面形状为竖直线型,见图1。文献[12-14]进行了Trapdoor试验,发现松动区滑动面形状是随着活门的移动量不断变化的,活动门位移量足够大的情况下才能达到Terzaghi所提出的竖直线型滑动面状态,在达到极限状态之前,滑动面形状为弧线状。盾构隧道的主要特点是在施工过程中对土体的扰动相对较小,在施工过程中,通过严格控制掘进面支护压力与壁后注浆压力等施工参数能够有效限制上覆地层的位移。当盾构隧道的覆土位移受到限制时,上覆土体出现不完全成拱的现象[7]。这种不完全成拱的现象本质上是上覆土体未达到主动破坏的极限状态,类似于Trapdoor试验中活动门的“小位移”情况,呈现“弧形破坏面”的状态。
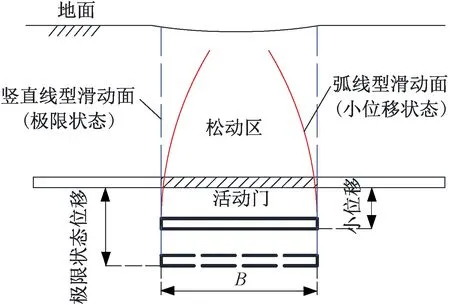
图1 活动门试验结果
现有的松动土压力计算理论中滑动面形状假设见图2。由图2可见,斜直线型滑动面假设与盾构隧道的实际滑动面形状不符;抛物线型滑动面假设虽适用于“弧形破坏面”的状态,但抛物线形状的数学表达式推导尚无相应的理论可依。
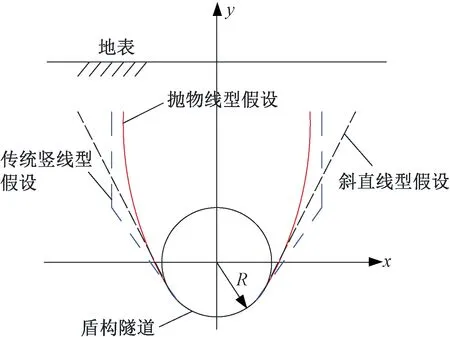
图2 滑动面形状的假设
针对上述情况,本文引入滑移线场理论对盾构隧道松动区的“弧形破坏面”进行分析。现在通用的平面应变滑移线场理论最初是由Kotter提出,随后经一大批著名学者的完善后,于21世纪60年代基本定型[15]。滑移线场理论广泛应用于边坡稳定性分析、土压力计算和地基承载力计算等。对于岩土材料,滑移线在数学上是双曲型微分方程的特征线,在宏观力学上是剪切破坏的应力迹线[16],如果松动区的滑动面边界上的应力状态均达到土体的抗剪强度,则滑动面的轨迹满足滑移线场理论中应力滑移线的特征。由上可知,使用滑移线场理论中的应力滑移线来描述滑动面的轨迹是可行的。综上,本文中假定“弧形滑动面”上的土体已达到其抗剪强度,通过求解应力滑移线得出“弧形滑动面”轨迹的数学表达式。
2 基于滑移线理论的滑动面形状表达式求解
经典的滑移场理论实际上隐含着一个假定,即材料服从相关联的流动法则,材料的剪胀角等于材料的内摩擦角,而大量实验表面岩土体并不服从相关流动法则,对于M-C准则的岩土介质,采用相关联的流动法则会人为扩大剪胀的作用。基于非关联流动法则假定进行滑移线的求解更为合理,所以本文采用基于非相关流动法则的滑移线场理论分析滑动面的应力轨迹线。
2.1 服从非关联流动法则的应力滑移线方程
理想塑性体的平面应变问题中,应力滑移线是各点上的剪切破坏面的连线,每点处存在两个相交的滑移线,见图3。
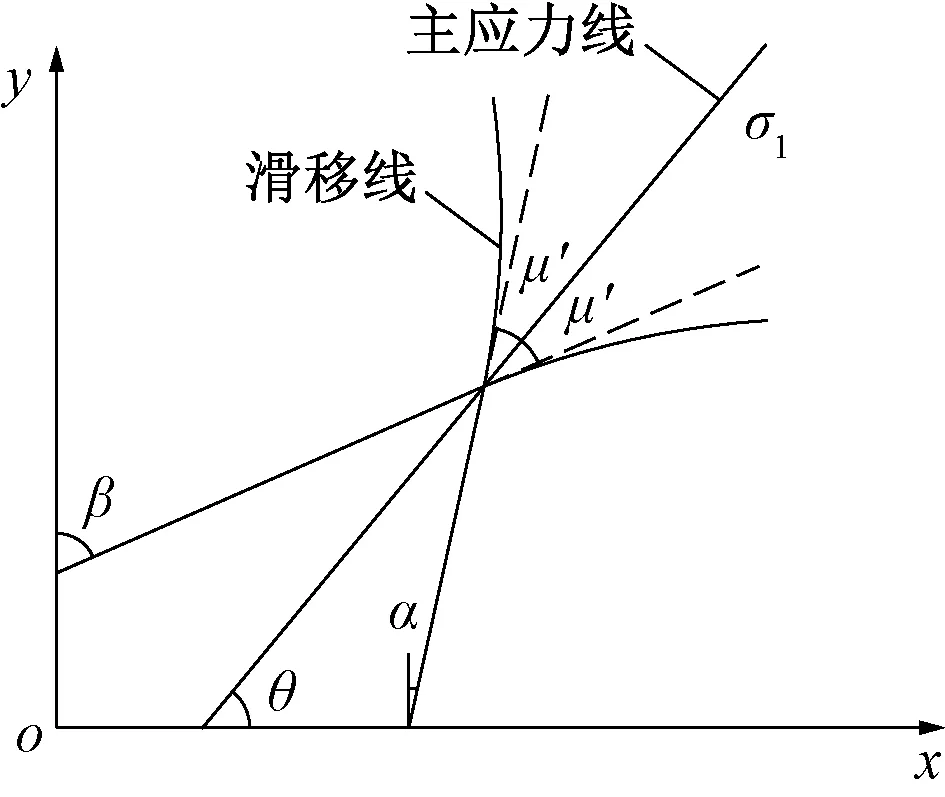
图3 滑移线与主应力线
α、β为滑移线与x、y轴的夹角,满足
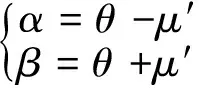
(2)
式中:θ为主应力与x轴夹角;μ′为剪应力与主应力的夹角。
对于M-C材料,在非相关流动法则的假定下,剪应力与主应力的夹角为[17]
(3)
式中:ψ为剪胀角,非关联流动法则的条件下,满足[18-19]
(4)
其中,η为剪胀系数,满足0≤η≤1。
由上所述,滑移线基本方程可表示为
(5)
2.2 应力滑移线求解
在均匀应力场中,θ为常数,在非均匀应力场中θ为变量。对于本文所提及的弧形滑动面,主应力线与x轴的夹角一定是不断变化的,属于非均匀应力场的情况。非均匀应力场中,由于岩土流动方向与应力滑移线成一角度,因而数学上应力滑移线为对数螺旋线[20-22]。因此,应力滑移线可假设为
r=r0exp[θA·tan(θB+ψ/2)]
(6)
式中:r为任意角下螺旋线上某点到极点距离;θA为极角;文献[21-22]认为θB为土体的膨胀角;r0为待定系数。
将式(6)转化为直角坐标系的形式,并进行微分,可得
(7)
由式(7)必须满足式(5),可得
(8)
θB计算式为[22]
(9)
将式(8)、式(9)代入式(6),可得基于非关联流动法则的应力滑移线方程为
(10)
2.3 盾构隧道的滑动面形状表达式求解
为求解式(10)中r0,本文作出如下假定:滑动破坏面终点与水平方向垂直;在非相关流动法则的条件下,滑动破坏面起始点处与水平方向的夹角θ1=π/4+ψ/2,O2点的速度矢量转动角为ψ,则∠O2Ox=ψ,见图4。

图4 本文的滑动面假设
由图4所示几何条件,可得
(11)
r1sinθ1=r0sin(ηφ)+Ha+R(1+sinθ1)
(12)
式中:Ha为成拱高度。
联立式(11)与式(12)求解,可得
(13)
将式(13)代入式(10),转换为直角坐标系,可得滑动破坏面的表达式为
(14)
式中:A1、A2为待定系数。
(15)
由式(14)可知对数螺线线型滑动面的表达式为含有隐函数的方程,难以直接用于松动土压力的解析求解。为了简化推导过程,本文将隧道顶到地面之间的滑动面简化为逼近的斜直线,如图4的中所示逼近线。
根据图4的几何关系,取盾构隧道圆心点处为坐标原点,求得斜直线的数学表达式为
y=A3·x+A4
(16)
式中:A3、A4为待定系数
(17)
(18)
其中,
(20)
3 松动土压力求解
3.1 侧压力系数
在滑动边界处,由于土体间摩擦力的影响,松动区边界处的主应力轴发生旋转,滑移面处的竖向应力σh与水平向应力σv已不再是主应力。本文基于主应力轴旋转理论求解滑动面上正应力σns与松动区竖向应力σv的数值关系,假定拱迹线为大主应力σ1轨迹,其形状为圆弧形,小主应力σ3方向偏转后其与水平向夹角为θm,见图5。

图5 主应力轴旋转示意图
垂直滑动面的主应力轴旋转理论中,滑动面上的剪切力完全发挥,考虑非关联流动法则时,小主应力σ3与水平方向的夹角为π/4+ψ/2,根据本文的滑动面假设,小主应力σ3与水平方向的夹角θm变化为
(21)
式中:θs为滑动面与竖直方向的夹角,由图4的几何关系可得
(22)
剪应力发展示意见图6。

图6 剪应力发展示意
由图6的摩尔应力圆可得
σh=σ1sin2θm+σ3cos2θm
(23)
σv=σ1cos2θm+σ3sin2θm
(24)
(25)
式中:τ为剪应力;θf为不完全发展的摩擦角。
最大主应力与最小主应力的关系为
(26)
式中:Kp为被动土压力系数。
联立式(25)、式(26)可得
(27)
由式(25)与式(27)可得剪应力与竖向应力的关系为
(28)
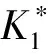
(29)
由图6可知,滑动边界上的正应力表达示为
σns=σvcos2θs+σhsin2θs+τsin2θs
(30)
将式(28)代入式(30),可得松动区内竖向应力与滑动面上正应力之间的关系为
(31)

(32)
其中,
(33)
3.2 松动区内竖向应力
在松动区内任一高度y处取厚度为dy、宽度为By的土条单元,见图7。土条单元受力包括:微分单元土体的自重γ;作用于上下边界的竖向应力σv与σv-dσv;作用于滑动面上的正应力σns和切向应力τns。

图7 土条单元受力状态
根据本文的滑动面假设,任一位置处土条单元的宽度By的表达式为
By=B1+2ytanθs
(34)
式中:
B1=2R(cotθ1+sinθ1)
(35)
在非关联流动的法则的条件下,文献[19]认为滑移线上正应力σ*和剪应力τ*具有类似于M-C准则的关系,表达式为
(36)
式中:强度参数c*、φ*和M-C准则中的c、φ具有相似的意义,它们之间的关系为
(37)
若土体满足非关联流动法则下的M-C破坏准则,滑动面上的切向应力τns可表示为
(38)
综上,由土条单元的竖向力平衡,可得
(39)
将式(31)、式(38)代入式(39),整理后可得
(40)
式中:
(41)
取初值条件为
σv|y=Ha+R=q
(42)
式中:q为地表荷载。
求解微分方程,并将初值条件代入,得出松动区内的竖向应力为
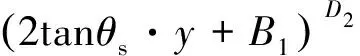
式中:D1、D2、D3分别为待定系数。
(44)
(45)
(46)
同理,对于考虑黏聚力的土体,松动区内的竖向应力表示为
(47)
式中:D4、D5分别为待定系数。
(48)
(49)
式中:c为土体的黏聚力。
4 算例分析
4.1 与现场实测结果的比较
为了验证本文计算模型的精确性,将计算结果与现场实测结果进行对比。现场实测地点位于苏州地铁某区间盾构隧道,监测断面处地质情况与测点布置见图8,该断面处管片外径为6.2 m,隧道顶部覆土厚度约为11.2 m,盾构穿越地层主要为粉细砂地层,相应地层主要物理力学指标见表1。

图8 监测点的布置(单位:m)

表1 地层物理力学指标
将现场实测结果,本文计算模型(剪胀系数η=1.0,服从关联流动法则)、传统竖直滑动面假设计算模型[1]、斜直线型滑动面假设计算模型[8-9]和抛物线型滑动面假设计算模型[11]的结果进行比较,见图9。由图9可知,本文得到的竖向应力分布形式与竖直线型、斜直线型和抛物线型计算模型的竖向应力分布形式一致,即竖向应力沿深度非线性分布,深度增大到一定程度后,竖向应力的增量开始减小,这是由于超过一定深度后,由摩擦作用引起的竖向应力的转移增大。
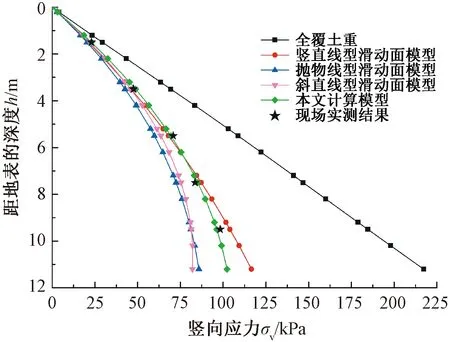
图9 计算结果与实测结果的比较
在覆土范围内,本文模型的计算结果与现场实测结果最为接近。在一定深度内,本文的模型与竖直线型模型的计算结果均接近于实测结果,但超过一定深度后,竖直线型模型的计算结果偏大,这是由于盾构隧道的覆土未达到临界破坏状态,深度越大,真实的松动区边界形状与垂直线形状的差异越大;另外,斜直线型和抛物线型模型的计算结果小于实测结果,主要原因在于此两种计算模型所假设的松动区范围远小于实际范围。
隧道洞顶土压力的理论计算结果与实测拟合结果见图10。由图10可知,抛物线型模型滑动面模型和斜直线型滑动面模型的结果小于实测拟合值,若采用这两种方法进行隧道顶部的荷载预测是不利于工程安全的;另外,对于背景工程,竖直线型滑动面模型(Terzaghi经典方法)的计算结果为116.56 kPa,本文方法的计算结果为102.28 kPa,现场实测拟合值为99.83 kPa,由此得知Terzaghi经典方法高估了隧道洞顶的土压力,本文方法与实测结果更为接近,相较于传统方法,本文模型能够提高隧道洞顶荷载的荷载预测精度。

图10 隧道洞顶土压力的理论计算结果与实测结果比较
4.2 剪胀系数对计算结果的影响
剪胀系数η取值小于1.0时,剪胀角ψ小于内摩擦角φ,土体不再服从相关流动法则。在非关联流动法则的条件下,计算参数同图9所用参数,计算不同的剪胀系数下松动区内的竖向应力分布,结果见图11。
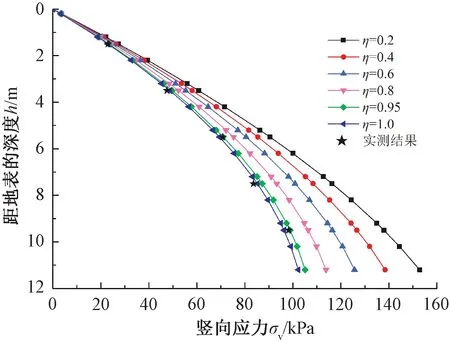
图11 不同剪胀系数下的计算结果
由图11可知,剪胀系数n<1.0时的竖向应力分布特征大致相同,剪胀系数n取值越大,松动区竖向应力分布的非线性越明显;另外,剪胀系数n取值越小,得出的松动区竖向应力越大,作用于盾构隧道顶部的松动土压力越大,这是由于本文的计算模型中,剪胀系数对滑动面的形状影响较大,影响见图12。由图12可见,剪胀系数越小,所得出的松动区宽度越大,导致作用于盾构隧道顶部的松动土压力值计算结果越大。

图12 不同剪胀系数下的滑动面
4.3 内摩擦角对计算结果的影响
不同内摩擦角下的竖向应力计算结果见图13,内摩擦角取值范围:10°~30°,其他计算参数取值同图9中所用参数。由图13可知,当内摩擦角较小时,竖向应力与自重引起的竖向应力分布较吻合。内摩擦角越大,竖向应力分布形式的非线性越为明显,这是由于滑动面上的剪切力随着内摩擦角的增大而变大,土拱效应越明显。
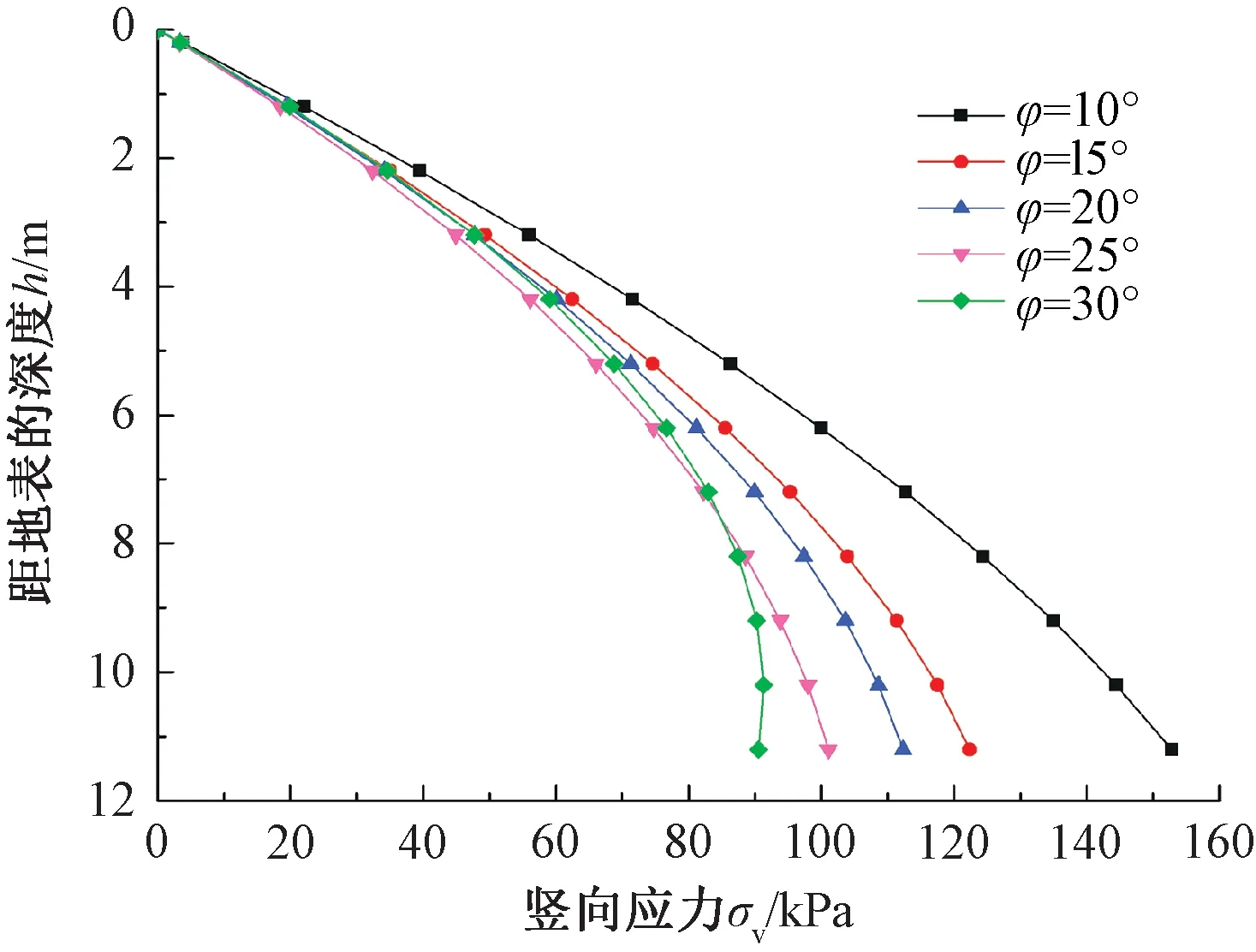
图13 不同内摩擦角下的计算结果
5 结论
本文主要采用理论解析的方法,对盾构隧道的松动土压力计算模型进行了研究,得到如下结论:
(1)引入滑移线场理论,考虑非关联流动法则,推导得出盾构隧道的松动区滑动面形状的数学表达式,根据受力平衡条件推导了松动区竖向应力的计算公式,并将本文方法与现场实测数据进行对比,验证了本文模型能够有效预测盾构隧道的松动土压力值。
(2)将多种计算模型与实测结果进行比较,根据计算结果,斜直线型和抛物线型模型的计算结果小于实测结果,主要原因在于此两种计算模型所假设的松动区范围远小于实际范围。
(3)根据参数分析结果:剪胀系数越小,基于本文方法所得出的松动区宽度越大,导致作用于盾构隧道顶部的松动土压力值计算结果越大。
本文的计算模型仅考虑盾构隧道覆土内滑动面发展至地表的情况,适用于浅埋条件;对于深埋的工况,由于松动区无法发展至地表,本文的计算方法将不再适用,尚须进一步研究。
