动车组车轮多边形磨耗发展历程模拟及车轮粗糙度的影响

宋志坤，任海星，胡晓依，刘元富,刘 伟,李 强

(1.北京交通大学 机械与电子控制工程学院， 北京 100044；2.中国铁道科学研究院集团有限公司铁道科学技术研究发展中心， 北京 100081)

近年来，我国动车组出现了车轮多边形化现象，当运行速度为300 km/h时，车轮表现出18～20阶多边形化[1]，当运行速度为250 km/h时，车轮多边形的主要阶次为23、24阶[2]，高阶车轮多边形磨耗导致轨道和车辆系统中的诸多问题。一方面，车轮多边形会产生高频轮轨冲击载荷，导致转向架零部件发生损坏或者失效，对动车组行驶安全产生重要影响。另一方面，车内噪声在300～400、500～600 Hz频率范围内存在声共振区域，一定车速下，车轮多边形磨耗激励频率处于此频段时，会使车辆系统的振动水平升高，进而激励车体内装板振动，产生振动辐射噪声[3]。因此，不得不在达到镟修里程前对车轮进行镟修，这缩短了车轮的使用寿命，增加了我国高速铁路的运营成本。

只有掌握车轮多边形的形成规律，才能从根本上控制高阶多边形的产生和发展。文献[4]分析了高速下理想1阶到5阶初始多边形磨耗的发展，结果发现多边形磨耗的发展很大程度上取决于轨道特征和激励频率。文献[5]利用车辆/轨道耦合动力学模型结合Archad磨耗模型，研究了地铁列车在直线轨道上的多边形演化历程。结果表明，5～7、14～20阶多边形的增长幅度最大。前者被认为与车辆/轨道耦合系统垂直共振有关，后者可能是由轨道垂直反振引起的。文献[6]通过试验研究了地铁车轮多边形磨耗的影响因素及增长规律，得出地铁车轮的9阶多边形磨耗是由于轮对的一阶弯曲振动引起的。文献[7]研究了轮对柔性对多边形磨耗的影响，发现在急弯轨道上，轮对的扭转模态可以促进多边磨耗的发展，而轮对弯曲模态对多边形磨耗没有促进作用。文献[8]指出轮轨系统摩擦自激振动是导致车轮多边形的主要原因之一。文献[9]研究发现车轮之间钢轨的三阶垂向弯曲共振，导致轮轨法向力在550～650 Hz之间周期性波动，是导致车轮多边形产生的主要原因。

目前，研究人员主要是通过试验与仿真的方法对车轮多边形产生机理进行相关的研究，对车轮多边形发展的整个历程及影响因素研究比较少。从实际应用的角度来看，确定车轮多边形磨耗发展的影响因素，进而提出相应的抑制措施具有重要的现实意义。

为了研究动车组车轮多边形磨耗发展的影响因素，本文建立考虑柔性轮对和柔性轨道的车辆/轨道耦合动力学模型，将其与Archard磨耗模型相结合建立长期磨损迭代模型。模拟动车组车轮多边形产生和发展的全过程，创造性地从车轮多边形整个发展历程的角度研究车轮粗糙度对车轮多边形发展的影响。

1 长期磨损迭代模型的建立

1.1 车辆/轨道耦合动力学模型

由于车轮多边形的激励频率通常较高，传统的多刚体动力学模型覆盖的频率有限，难以满足仿真要求，因此结合有限元软件Ansys与多体动力学软件SIMPACK建立考虑柔性轮对和柔性轨道的车辆/轨道耦合动力学模型[10]。

首先使用多体动力学软件SIMPACK，以某型动车组为研究对象，建立多刚体动力学模型。建立轮对的有限元模型如图1所示。将车轮与车轴视为整体部件，不考虑车轮与车轴的过盈配合关系。整体轮对采用六面体网格划分，单元类型为3D实体单元Solid45。车轮直径为920 mm，踏面廓形为S1002CN，轮对的弹性模量为2.1×105MPa，泊松比为0.3，密度为7.85×103kg/m3。将构建好的柔性轮对模型通过SIMPACK中的FLEXBODY模块导入替换掉刚性轮对。

图1 轮对有限元模型

建立柔性轨道不仅需要建立钢轨的有限元模型，还需要编写柔性轨道的配置文件，利用SIMPACK软件中的FLEXTRACK模块读取配置文件以实现柔性轨道的导入。钢轨廓形采用60 N型钢轨，轨枕间距为0.63 m，轨枕、扣件、道床等轨下结构统一采用弹簧阻尼元件模拟，钢轨的弹性模量、密度、泊松比等参数设置与轮对保持一致，轨道端部采用大刚度、大阻尼进行固定。最终获得的车辆动力学模型见图3。

图2 车辆/轨道耦合动力学模型

1.2 轮轨接触模型

为了研究动车组在运行过程中的高频振动，建立考虑柔性轨道和柔性轮对的车辆/轨道耦合动力学模型，轮轨接触几何计算仍然按照传统的轮轨接触几何方法——迹线法[11]进行计算，轮轨法向接触问题采用Hertz接触理论进行计算，轮轨切向接触问题采用FASTSIM算法进行计算。

在车辆动力学模型中，普遍把Hertz理论应用于法向接触问题的求解，这是因为在很多情况下，采用Hertz理论计算法向接触问题速度较快且精度也满足要求。用于轮轨切向力计算的滚动接触蠕滑率/力模型中大多数是基于Hertz接触理论。因此，本文也采用Hertz接触理论，假设轮轨接触斑为椭圆。

(1)

根据弹性力学和静电势问题相似的假设，可以将椭圆接触斑内的压应力看作根据半椭球高度的坐标来变化，因此接触斑内的压应力分布可以表示为

(2)

式中：pz(x,y)为接触斑内坐标为(x,y)的点承受的压应力；N为轮轨法向力；a、b分别为椭圆的纵、横向半轴长。

对于切向接触问题，采用FASTSIM算法[12]，在该算法中法向应力分布与Hertz理论中法向应力半椭球式的分布有所不同，若把Hertz理论中的法向应力分布应用于FASTSIM算法中会产生较大的误差。因此Kalker从Hertz理论中提取a、b，提出了适合FASTSIM算法的法向应力计算式为

(3)

为了便于计算接触斑内切应力以及滑动速度分布，需要将接触斑离散为多个单元，每个单元内压应力、切应力以及滑动速度等参数保持一致。文献[13]认为将接触斑划分为10×10个单元就可以比较合理地区分出黏着区和蠕滑区以及压应力、切应力的分布情况。文献[14]研究表明，计算精度随着单元格划分数量的增加而提高。因此将接触斑沿纵、横向均匀划分为100×100个单元，单元格纵、横向长度分别为Δx、Δy。

1.3 磨耗模型

在众多计算磨耗模型中，Archard磨耗模型因为其较快的计算速度和较好的计算精度被广泛采用，Archard磨耗模型的定义为

(4)

式中：Vwear为磨耗材料体积；Kw为无量纲的磨耗系数，由接触压力和相对滑动速度共同决定；N为两物体间的法向接触力；d为两接触物体的相对滑动距离；H为两接触物体中较软材料的硬度，在本文中为车轮表面硬度。对于踏面磨耗，磨耗系数在1×10-4～10×10-4范围内，对于轮缘磨耗，磨耗系数在1×10-4～400×10-4之间变化[8]。本文仅研究动车组在直线轨道上的运行情况，轮轨间相对滑动较小，因此假设磨耗系数为常数，取为1×10-4。

为了深入研究接触斑内磨耗分布情况，可将Archard磨耗模型结合FASTSIM算法得出接触斑内磨耗深度的计算式为

(5)

式中：Δz(x,y)为中心坐标为(x,y)的单元格的磨耗深度；ξ1、ξ2、ξ3分别为纵向、横向、自旋蠕滑率；ux、uy分别为纵向、横向的弹性滑动量。

使用Matlab编写程序建立磨耗模型，提取车辆/轨道耦合动力学模型计算出的动力学数据，将其代入到磨耗模型中，计算出接触斑内磨耗深度分布见图3。磨耗深度为0的区域是黏着区，不为0的区域是蠕滑区，在黏着区和蠕滑区的交界处磨耗深度达到最大，在黏着区的末端磨耗深度趋于0。

图3 接触斑内磨耗深度分布

2 车轮多边形发展历程模拟

为研究车轮圆周上磨耗分布情况，将车轮滚动圆均匀离散为3 600个点，每两个采样点之间相隔0.1°，对接触斑内的磨耗深度进行纵向叠加，取平均值表示车轮旋转一圈产生的磨耗积累量。

(6)

式中：Δzk为滚动圆上第k个离散点的磨耗深度；Δz(i,j)为接触斑上纵向第i、横向第j个网格的磨耗深度；MM为接触斑纵向划分的网格数；NN为接触斑横向划分的网格数。

计算完这3 600个采样点的磨耗量后使用40阶傅里叶级数对磨耗进行拟合，可以获得车轮圆周上的磨耗情况，傅里叶级数表达式为

x∈(0,2π)

(7)

式中：N为傅里叶级数的阶次，高阶车轮多边形的阶次一般不超过30，因此，本文N取40。

假设在短距离运行中车轮的磨耗累积量与行驶距离成线性增长，可以将车轮旋转一圈产生的磨耗量乘以放大系数用来表示车轮运行一段距离产生的磨耗量。文献[8]在计算时放大系数取1×106。一般来讲，放大系数的取值越小，计算出的结果与实际越相符。因此，本文中放大系数取2×105，即动车组运行578 km产生的磨耗累积量。以初始车轮多边形减去这个磨耗量获得一个新的车轮多边形，将这个新的多边形代入到车辆动力学模型中，不断重复上述过程就可以获得车辆长距离运行中车轮多边形的发展过程，这个迭代多次以获取车轮多边形长期磨耗的模型被称之为长期磨损迭代模型。

使用长期磨损迭代模型，以实测初始车轮多边形作为输入，未考虑轨道不平顺，模拟动车组运行速度分别为250、300 km/h时，车轮多边形的发展历程，磨耗累积量的极坐标分布见图4。应用40阶傅里叶级数对车轮多边形进行拟合，利用车轮踏面粗糙度水平计算公式得出车轮表面粗糙度的阶次变化图。粗糙度水平计算式为

图4 速度为250、300 km/h磨耗累积

(8)

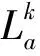
速度为250、300 km/h粗糙度水平阶次变化见图5。

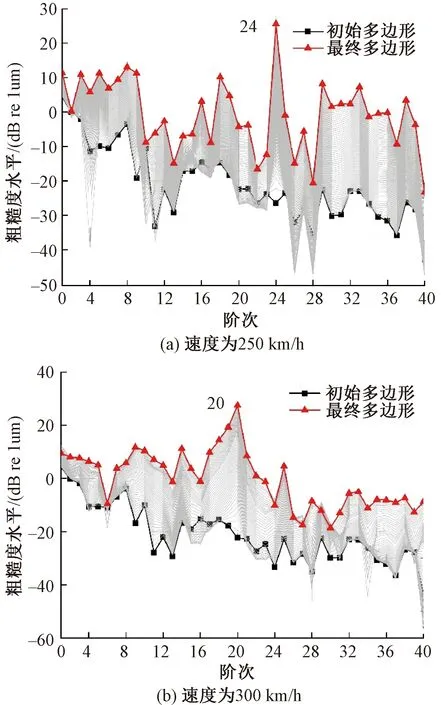
图5 速度为250、300 km/h粗糙度水平阶次变化

文献[2]现场试验发现当列车以速度250 km/h运行时产生的车轮多边形阶次为23、24阶；当列车运行速度为300 km/h时，文献[1]对不同轮径下车轮多边形阶次进行统计分析发现，轮径为860～890 mm的车轮主要由19阶多边形磨耗主导，而轮径为900～920 mm的车轮主要由20阶多边形磨耗主导。

由图5(a)可知，当动车组以250 km/h速度运行时，车轮多边形最终以24阶主导。由图5(b)可知，当动车组以速度300 km/h运行时，车轮多边形最终以20阶主导。这一现象与动车组实际运行中产生的多边形特征相吻合，验证了长期磨损迭代模型的正确性。

根据实测数据与仿真结果发现，当动车组以250、300 km/h速度运行时，最终产生的车轮多边形主导阶次分别为20、24。频率计算式为

(9)

式中：f为激励频率；n为多边形阶次；v为动车组运行速度；r为车轮名义滚动圆半径。

由式(9)计算得出多边形导致的激励频率约为580 Hz，说明在轮对和钢轨之间存在一个固定的振动频率，其应属于结构模态频率，这个振动频率的存在促进了车轮多边形的产生和发展。由式(9)可以发现，多边形最终发展的阶次与动车组运行速度有关，随着速度的改变，多边形的主导阶次会随之发生改变。

3 车轮粗糙度的影响

本文通过长期磨损迭代模型模拟动车组以250、300 km/h速度运行一段距离车轮多边形的发展情况，结果与实际情况相吻合。因此可采用该模型深入研究车轮粗糙度对车轮多边形发展历程的影响。

动车组在长时间运行后，车轮上会产生多种磨耗损伤，包括车轮多边形、踏面磨耗与轮缘磨耗等，这会导致动车组在运行过程中异常振动，影响行车安全。因此需要定期对车轮进行镟修，但由于镟修装置以及各种人为原因导致镟修后的车轮周向并不是完美的正圆，仍然存在一些多边形，这可能会对车轮多边形的发展产生影响。因此本文选取了镟修质量不同的车轮上存在的两种初始车轮多边形，使用长期磨损迭代模型研究其对车轮多边形发展的影响。镟修质量不同的两种初始多边形见图6，其中镟修质量较差的车轮残留了高阶多边形。

图6 两种不同镟修质量的车轮多边形

将这两种初始车轮多边形作为输入，未考虑轨道不平顺，分别计算其车轮多边形的发展情况。运行速度设置为300 km/h，进行30次迭代后的发展情况见图7。由图7可见，镟修质量较差的车轮粗糙度水平在24 dB附近，镟修质量较好的车轮粗糙度水平在16 dB附近。对比之下可以发现，对于镟修质量较差的车轮，多边形发展速度比镟修质量较好的车轮更快，导致最终车轮多边形的粗糙度水平也更高。因此，提升镟修质量，控制初始车轮不平顺对于抑制车轮多边形具有重要的作用。

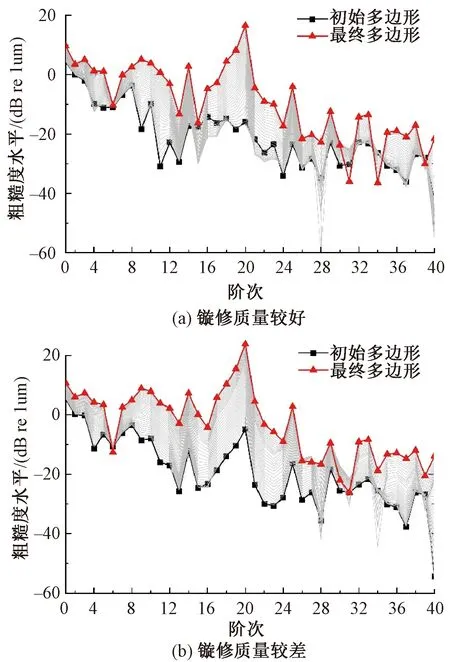
图7 两种镟修质量下粗糙度水平发展过程

4 结论

本文建立考虑柔性轮对与柔性轨道的车辆/轨道耦合动力学模型，利用Matlab与SIMPACK联合仿真将动力学模型与Archard磨耗模型相结合，建立长期磨损迭代模型。使用长期磨损迭代模型研究速度变化对车轮多边形发展的影响，创造性地从车轮多边形的整个发展历程角度分析车轮粗糙度对车轮多边形发展的影响，得到如下结论：

(1)使用长期磨损迭代模型模拟了动车组运行速度为250、300 km/h时车轮多边形的整个发展历程，发现车轮由最初无明显高阶多边形发展到分别以24、20阶多边形占主导，这一现象与动车组实际运行过程中产生的车轮多边形特性相似，验证了长期磨损迭代模型的正确性。

(2)使用频率计算公式发现，车轮多边形的激励频率约为580 Hz，这说明在轮对和钢轨之间存在一个固定的振动频率，这个振动频率的存在促进了车轮多边形的产生和发展。

(3)车轮初始多边形中是否残留着高阶多边形是衡量镟修质量好坏的一个重要指标，对比研究了镟修质量的好坏对车轮多边形发展的影响，结果发现在相同条件下提高镟修质量可以在一定程度上抑制车轮多边形的发展速度。