弹性分开式扣件板下组合静刚度设计影响因素分析

韦 凯，赵泽明，王 显，江万红，王 平

(1.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；2.西南交通大学 土木工程学院，四川 成都 610031；3.中铁二院工程集团有限责任公司，四川 成都 610031)

随着我国经济水平的快速提高，我国轨道交通事业得到了长足发展。扣件系统作为轨道结构的重要组成部分，具有联结钢轨和轨枕、保持轨道几何形位、提供轨道弹性等作用[1]。弹性分开式扣件系统因其扣压力大、安装方便、扣件组合静刚度低等特点被广泛用于我国轨道交通建设中[2]。

传统弹性分开式扣件板下组合静刚度设计方法中假设铁垫板为绝对刚性体，即不考虑铁垫板在锚固螺栓紧固时产生的翘曲变形[3]。根据该假设，传统设计方法往往通过均匀加载测得板下垫板静刚度来近似评价板下组合静刚度大小。同时，文献[3]指出由于铁垫板在实际情况下会发生翘曲变形，这将导致板下组合静刚度实测结果显著小于传统板下组合静刚度设计结果，尤其是在锚固螺栓紧固扭矩较大的情况下。但是文献[3]并未明确指出不同紧固扭矩情况下板下组合静刚度实际值与传统设计值的误差范围，以及是否能够满足工程使用的精度要求等。此外，铁垫板产生的翘曲变形会导致板下垫板处于非均匀受压状态，同时板下垫板又是具有明显非线性弹性特征的高分子材料[4-5]，因此在非均匀受压情况下，板下垫板并非为铁垫板提供均匀的支承刚度。总之，采用传统设计中均匀加载方式得到的板下垫板静刚度与实际服役状态下板下垫板所提供的支承刚度明显不同。

为了完善现有弹性分开式扣件板下组合静刚度的设计理论，本文以我国地铁常用的DZⅢ型弹性分开式扣件为研究对象，首先通过力学试验机测试不同紧固扭矩条件下该类弹性分开式扣件板下组合静刚度，并将实测结果与传统设计方法中均匀加载得到的板下垫板静刚度进行对比，证明铁垫板翘曲变形与板下垫板非线性弹性是导致传统弹性分开式扣件板下组合静刚度设计方法产生误差的主要原因。其次，为了研究铁垫板翘曲变形与板下垫板非线性弹性对板下组合静刚度设计的影响规律，建立了板下组合结构三维非线性有限元模型，在板下组合静刚度理论计算与室内测试结果的对比验证基础上，进一步研究了单独或综合考虑铁垫板翘曲变形与板下垫板非线性弹性特征对板下组合静刚度设计的影响规律及其影响程度，以期对弹性分开式扣件系统的板下组合静刚度设计提供理论指导。

1 扣件系统及刚度设计方法介绍

1.1 DZⅢ型扣件系统

DZⅢ型弹性分开式扣件系统组合结构见图1，主要由e形弹条、轨距挡块、轨下弹性垫板、铁垫板、板下垫板、锚固螺栓、双层弹簧垫圈、调距扣板和预埋套管等组成。e形弹条将钢轨固定于铁垫板上，锚固螺栓将铁垫板固定于混凝土轨枕上，从而避免了更换弹条或钢轨对轨枕的扰动。根据轨道结构线形不同，锚固螺栓的紧固扭矩也有所区别。在直线地段锚固螺栓紧固扭矩设计值为150～200 N·m，在曲线地段锚固螺栓紧固扭矩设计值为200～250 N·m。

图1 DZⅢ型扣件组合图

1.2 传统弹性分开式扣件组合刚度设计方法

传统弹性分开式扣件组合静刚度理论模型见图2。该设计方法假设铁垫板为刚性体，因此板下垫板均匀受压。扣件系统的节点静刚度Ka由铁垫板以上部分的组合静刚度与铁垫板以下部分的组合静刚度串联组成，见式(1)。

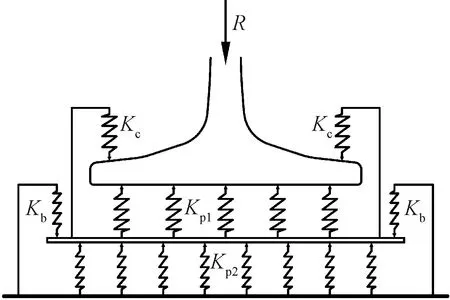
图2 弹性分开式扣件组合静刚度理论模型

(1)

式中：Ka1为板上组装静刚度；Ka2为板下组合静刚度。

板上组合静刚度Ka1由轨下弹性垫板静刚度Kp1与弹条的卸载刚度Kc并联组成。板下组合静刚度Ka2由板下垫板静刚度Kp2与螺栓的卸载刚度Kb并联组成。Ka1、Ka2计算式分别为

Ka1=Kp1+2Kc

(2)

Ka2=Kp2+2Kb

(3)

由于锚固螺栓卸载刚度较小，因此，常将板下垫板静刚度近似视为板下组合静刚度。

基于传统弹性分开式扣件组合刚度设计方法，文献[6-7]计算了DZⅢ型扣件在不同紧固扭矩作用下锚固螺栓对铁垫板产生的预紧力，并参考规范(GB/T 21527—2008)《轨道交通扣件系统弹性垫板》[8]中的静刚度测试方法，采用均匀加载的方式对板下垫板静刚度Kp2进行了测试。本文将结合该文献中的测试结果，与板下组合静刚度Ka2实测结果进行对比分析，并开展弹性分开式扣件板下组合静刚度设计影响因素的研究。

2 试验测试与分析

以氯丁橡胶板下垫板为例，应用力学试验机对DZⅢ型扣件系统不同紧固扭矩下的板下组合静刚度进行测试，同时记录荷载施加过程中铁垫板不同位置处的位移，揭示铁垫板翘曲变形的程度。将不同紧固扭矩条件下均匀加载方式得到的板下垫板静刚度Kp2与板下组合静刚度Ka2实测结果进行对比，明确传统板下组合设计刚度与实际刚度的误差范围，展现铁垫板翘曲变形与板下垫板非线性弹性对弹性分开式扣件板下组合静刚度设计的影响程度。

2.1 试验准备

试验设备及配件主要包括DZⅢ型铁垫板、氯丁橡胶板下垫板、双层弹簧垫圈、调距垫板、锚固螺栓以及力学试验机。首先，对板下结构进行组合，通过锚固螺栓将双层弹簧垫圈、调距垫板、铁垫板、板下垫板固定于混凝土短轨枕上，并应用扭矩扳手对锚固螺栓施加紧固扭矩，使之达到设计安装状态。然后，将板下组合结构置于力学试验机测试平台上，按照相应的测试方法对板下组合静刚度进行测试。

2.2 测试流程

由于目前针对弹性分开式扣件板下组合静刚度测试暂无相关规范明确规定，因此，本文借鉴文献[9]中扣件系统组合静刚度相关测试方法展开测试。

正式加载前，先将百分表调零，并以3 kN/s的加载速度对板下组合结构进行3次0 ～ 60 kN的预加载，以消除板下垫板高分子材料的Mullins效应[10]。然后，再以2 kN/s的加载速度进行正式加载，当施加至单组扣件承担的车辆荷载50 kN时保持60 s，待百分表读数稳定后，记录其变形结果。重复以上试验流程2次，取3次测试结果平均值，板下组合静刚度计算式为

(4)

式中：F1、F2分别为起始荷载0 kN、终点荷载50 kN；D1、D2分别为起始荷载、终点荷载对应的百分表位移读数。

为探究铁垫板在板下组合静刚度测试时产生翘曲变形的程度，沿铁垫板锚固螺栓孔对角线上分别设置了6个测点。测点1-1、1-2分别位于钢轨轨底外侧5 mm且距铁垫板边缘40 mm处的铁垫板上；测点2-1、2-2分别位于铁垫板边缘5 mm处，见图3(a)；测点3-1、3-2分别位于钢轨轨底上方内侧5 mm处，见图3(b)。由于铁垫板在锚固螺栓紧固作用下已发生向上的翘曲变形，钢轨在施加50 kN荷载情况下可近似视为刚性体，不考虑弹性变形。因此，测点3-1、3-2位置处垂直位移的平均值可间接反映铁垫板中部的垂向位移。板下组合静刚度评价时，采用测点3位置处的位移变形进行计算。

图3 铁垫板翘曲变形测点布置

2.3 测试结果

荷载施加后铁垫板不同位置的位移变形见图4，图中所示垂向位移为负代表向下变形，垂向位移为正代表向上变形。不同紧固扭矩条件下变形规律相同，这里仅对螺栓紧固扭矩为250 N·m的工况进行展示。从图4可以看出，铁垫板在车辆荷载作用下发生了明显的不均匀变形，最大变形位于铁垫板中部，变形值为0.89 mm(即测点3-1与测点3-2变形的平均值)；最小变形位于铁垫板边缘处，变形值为0.12 mm，二者相差0.77 mm。试验证明铁垫板产生的不均匀变形与传统设计方法中的变形假设存在明显差异。因此，在板下组合静刚度设计时，不应将铁垫板视为刚性体。

图4 铁垫板不同测点位置变形

不同紧固扭矩情况下，板下组合静刚度实测结果见图6，其中，均匀加载测得的板下垫板静刚度参考文献[7]。从图5可以看出，板下组合静刚度Ka2实测结果与板下垫板静刚度Kp2均随着紧固扭矩的增加相应提高。当紧固扭矩分别为150、200、250 N·m时，板下组合静刚度与板下垫板静刚度分别为44.5、54.1、60.0 kN/mm与61.3、84.2、116.6 kN/mm。

图5 板下垫板静刚度与板下组合静刚度实测值

通过对比板下组合静刚度Ka2实测结果与板下垫板静刚度Kp2可以发现，板下组合静刚度随紧固扭矩的增长规律与传统设计方法明显不符。在传统设计方法中，板下组合静刚度Ka2由板下垫板均匀加载得到的静刚度Kp2与锚固螺栓卸载刚度Kb两部分组成，即在任何扭矩情况下板下组合静刚度Ka2均应大于板下垫板的静刚度Kp2，见式(3)。而实测结果表明：在紧固扭矩为150 ～ 250 N·m范围内，板下组合静刚度Ka2实测结果均小于板下垫板均匀加载得到的静刚度Kp2，并且该结论与文献[3]中所述考虑铁垫板翘曲时实测结果小于设计结果的规律一致。当紧固扭矩分别为150、200、250 N·m时，板下组合静刚度传统设计值与实测值至少相差37.8%、55.9%与94.3%，无法满足工程设计要求。

3 板下组合静刚度有限元分析

为分析铁垫板翘曲变形与板下垫板非线性弹性特征对弹性分开式扣件板下组合刚度设计的影响，本文借助有限元软件ABAQUS，建立了板下组合结构非线性有限元模型进行分析。该模型将铁垫板考虑为弹性体，可仿真荷载施加过程中产生的翘曲变形；同时，板下垫板力学参数采用实测荷载-位移曲线[6]，可反映高分子材料的非线性弹性特征。在研究各因素对板下组合静刚度设计结果的影响规律之前，首先对板下组合静刚度测试流程进行仿真，并将仿真结果与实测结果进行对比，验证有限元模型的正确性；然后，分别研究铁垫板翘曲变形与板下垫板非线性弹性单一因素对板下组合静刚度设计的影响规律，并明确各因素产生的设计误差范围。

3.1 板下组合结构模型建立与验证

3.1.1 有限元模型建立

板下组合结构非线性有限元模型主要包括铁垫板、板下垫板、混凝土轨枕三部分。其中，铁垫板、混凝土轨枕采用线弹性模型，相关力学参数见表1。采用八节点六面体单元对铁垫板及混凝土轨枕进行网格划分，单元尺寸为5 mm。由于板下垫板在荷载施加过程中会产生较大变形，故采用了适用于橡胶类高分子材料大变形分析的Yeoh超弹性模型[11-13]，该模型参数通过有限元软件中输入的实测荷载-位移曲线拟合得到，本次采用氯丁橡胶拟合得到的模型参数分别为C10=0.303、C20=-0.028、C30=0.001 8。均匀加载条件下拟合得到的板下垫板荷载/位移曲线与实测结果[6]的对比情况见图6。同时，为了提高板下垫板的网格划分质量，采用了四结点线性四面体杂交单元对板下垫板进行划分，单元尺寸为5 mm。

表1 有限元模型参数

该模型通过约束铁垫板锚固螺栓孔位置处的纵向与横向变形，等效模拟锚固螺栓对铁垫板的固定作用，混凝土轨枕底部则采用了全约束方式，见图7。同时，铁垫板、板下垫板、混凝土轨枕之间均采用了罚函数接触算法来处理板下垫板大变形导致的不收敛问题[14]。在荷载施加方面，由于该三维有限元模型主要用于研究铁垫板及板下垫板的受力特征与变形情况，故将锚固螺栓紧固扭矩产生的预紧力在调距扣板面积范围内均匀施加至铁垫板上。荷载施加主要分为两步，首先施加锚固螺栓紧固扭矩产生的预紧力[6]，作用区域为铁垫板上调距扣板范围内，见图7(a)；然后施加车辆荷载，作用区域为铁垫板中部与钢轨轨底接触的区域，见图7(b)。

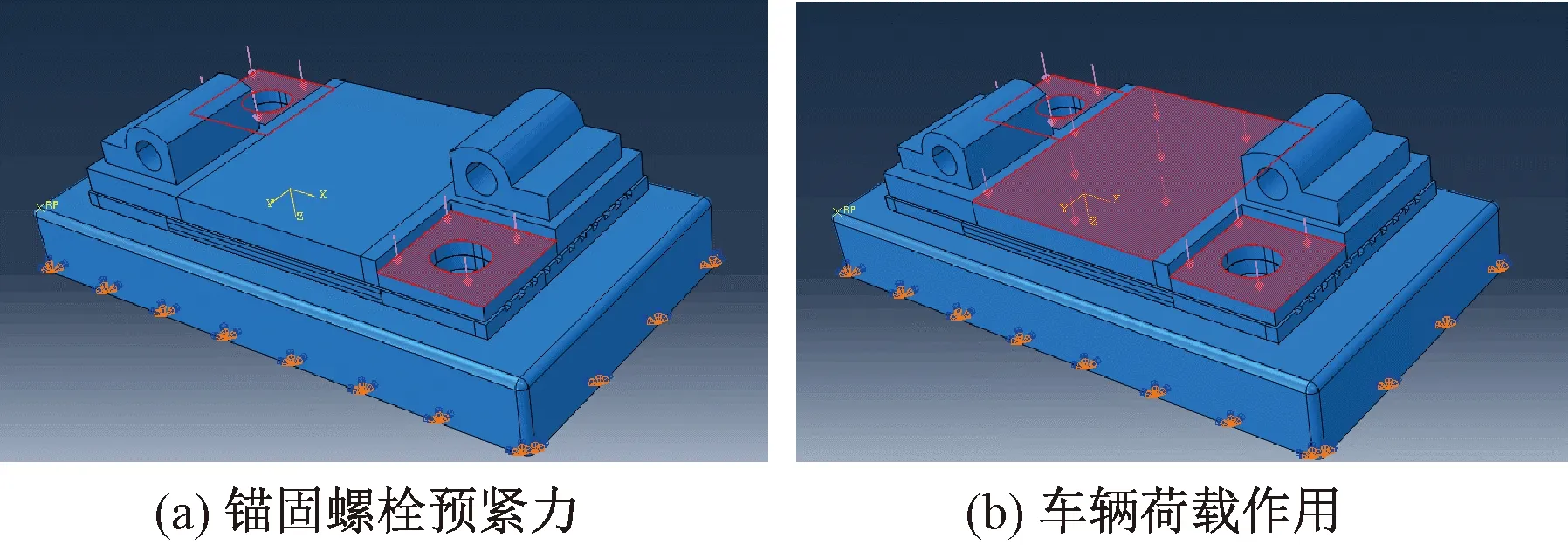
图7 板下组合静刚度荷载仿真设置

3.1.2 有限元模型验证

在锚固螺栓紧固扭矩作用下，铁垫板与板下垫板产生的位移变形见图8(a)；叠加车辆荷载作用后，铁垫板与板下垫板位移变形见图8(b)，不同紧固扭矩条件下变形规律相同，这里仅展示锚固螺栓紧固扭矩为250 N·m的工况。从图8可以看出，无论是在锚固螺栓紧固扭矩作用还是在车辆荷载作用下，铁垫板始终处于向上的翘曲变形状态，并且板下垫板始终非均匀受压，锚固螺栓孔位置处压缩程度最大，铁垫板中部位置处压缩程度较小。

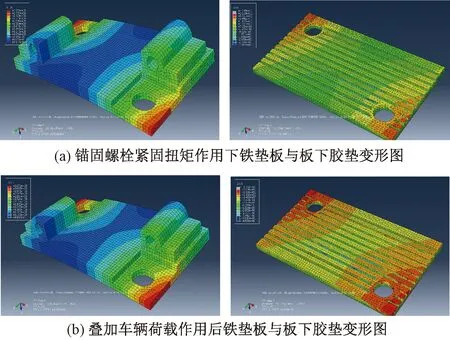
图8 板下组合结构真实变形

在锚固螺栓紧固扭矩以及车辆荷载作用下，铁垫板锚固螺栓孔对角线上的变形见图9(a)，相比铁垫板仅在锚固螺栓紧固扭矩作用下的翘曲变形而言，叠加车辆荷载作用后铁垫板的翘曲变形有所缓解。车辆荷载作用前后，铁垫板不同位置处位移变形仿真结果与实测结果对比见图9(b)，相同位置处有限元计算结果与实测结果基本一致。从板下垫板非均匀变形情况来看，在施加车辆荷载后，锚固螺栓孔位置处的位移变形为0.12 mm，小于相同扭矩均匀加载条件下的变形0.41 mm[6]，且小于板下垫板中部的位移变形0.82 mm，即锚固螺栓孔位置处的板下垫板实际刚度大于相同紧固扭矩情况下均匀加载得到的垫板刚度，且大于板下垫板中部位置处的实际刚度。因此，板下组合静刚度设计时需要考虑由铁垫板翘曲变形引起的板下垫板支承刚度不同的影响。

图9 铁垫板不均匀变形对比验证

不同紧固扭矩情况下，板下组合静刚度仿真计算结果与实测结果对比见图10。当同时考虑铁垫板翘曲变形与板下垫板非线性弹性因素影响时，不同紧固扭矩下板下组合静刚度设计值与实测结果基本相同。紧固扭矩为150、200、250 N·m时，板下组合静刚度设计值分别为43.7、52.7、61.1 kN/mm，与实测结果误差分别为1.8%、2.4%、1.9%，可满足工程设计误差要求，同时也验证了有限元模型的正确性。

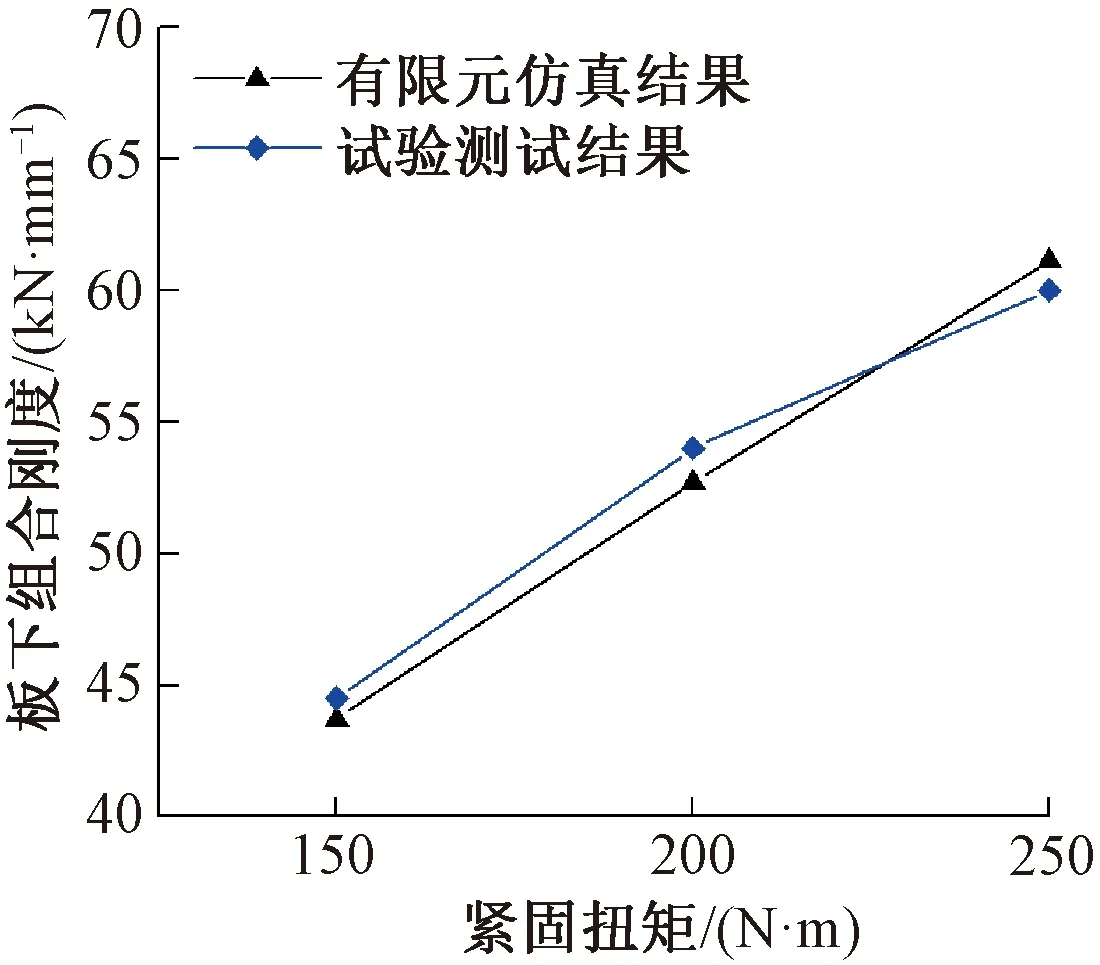
图10 板下组合静刚度对比验证

3.2 设计因素影响分析

为进一步分析铁垫板翘曲变形与板下垫板非线性弹性单一因素对板下组合静刚度设计的影响规律，计算工况见表2。其中，工况1～3不考虑铁垫板翘曲变形因素，仅分析板下垫板非线性弹性在不同紧固扭矩情况下对板下组合静刚度设计的影响。仿真分析时，将有限元模型中的铁垫板设置为刚性体，板下垫板仍采用Yeoh超弹性模型，以反映其非线性弹性。工况4～6不考虑板下垫板非线性弹性特征，仅分析铁垫板翘曲变形因素在不同紧固扭矩情况下对板下组合静刚度设计的影响。此时，有限元模型中将铁垫板考虑为弹性体，板下垫板采用线弹性模型，垫板刚度为文献[6]中对应扭矩情况下均匀加载得到的割线刚度，见图5。

表2 计算工况

当仅考虑板下垫板非线性弹性因素时，不同紧固扭矩条件下板下组合静刚度设计值见图11。由于铁垫板被考虑为刚性体，在相同荷载大小的情况下，无论是采用均匀加载方式还是按照实际荷载分布方式进行加载，对测试结果均不会造成影响，所以该设计结果与均匀加载得到的板下垫板静刚度基本相同。当紧固扭矩分别为150、200、250 N·m时，板下组合设计刚度分别为62.6、82.4、114.4 kN/mm，与板下垫板静刚度相差2.1%、2.2%、1.8%，与板下组合静刚度实测结果相差40.6%、52.6%、90.7%。由此可见，仅考虑板下垫板非线性弹性，对提高板下组合静刚度设计精度几乎没有影响，不同紧固扭矩情况下仍无法满足工程设计使用要求。

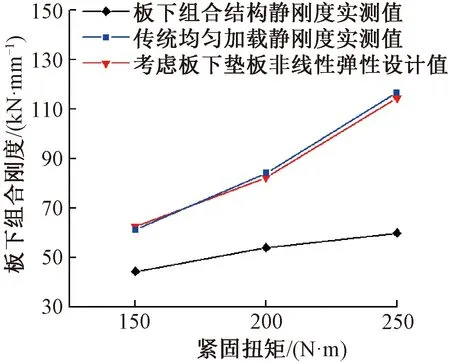
图11 仅考虑板下垫板非线性因素

在仅考虑铁垫板翘曲变形，不考虑板下垫板非线性弹性因素时，不同紧固扭矩情况下设计刚度与实测结果对比见图12。当紧固扭矩分别为150、200、250 N·m时，板下组合设计刚度分别为45.2、58.5、76.9 kN/mm，与板下组合静刚度实测值相差1.6%、8.2%、28.3%。可以看出，相比仅考虑板下垫板非线性弹性而言，仅考虑铁垫板翘曲变形因素时的板下组合静刚度设计误差明显减小，尤其是紧固扭矩较低的情况。然而，设计误差随着紧固扭矩的提高不断增大，在扭矩较大时仍无法满足工程设计使用要求。这是因为在紧固扭矩较小时，板下垫板不均匀受压程度较小，并且板下垫板基本处于线弹性阶段。设计时采用均匀加载得到的割线刚度与实际情况下板下垫板静刚度大小较为接近，所以设计误差较小。当紧固扭矩较大时，由于板下垫板在均匀加载条件下非线性弹性阶段的割线刚度大于实际情况下板下垫板中部位置处的刚度，所以导致板下组合静刚度设计值大于板下组合静刚度实测结果。此外，随着紧固扭矩的提高，氯丁橡胶材料的非线性增强，铁垫板中部位置处采用的均匀加载得到的割线刚度相比真实值更大，从而导致设计误差随着紧固扭矩的提高而不断增大。

图12 仅考虑铁垫板翘曲变形因素

结果表明，针对弹性分开式扣件系统，板下组合静刚度设计方法无论忽略铁垫板的翘曲变形还是忽略板下垫板的非线性弹性，都将会导致板下组合静刚度设计结果与实际结果产生较大误差，无法准确反映板下组合静刚度随紧固扭矩的变化规律。铁垫板翘曲变形与板下垫板非线性弹性在荷载作用过程中是相互影响相互作用的两个因素，铁垫板的翘曲变形导致板下垫板不同位置处的压缩状态不同，板下垫板非均匀压缩导致不同位置处刚度不同，从而又将进一步影响铁垫板的翘曲变形。因此，板下组合静刚度的设计必须同时考虑铁垫板翘曲变形以及板下垫板非线性弹性因素的影响。

4 结论

本文通过试验测试与有限元仿真方法，研究了弹性分开式扣件板下组合结构各部件的真实服役情况。对比了板下组合静刚度实测结果与传统板下组合刚度设计结果的差异，研究了铁垫板翘曲变形与板下垫板非线性弹性因素对板下组合静刚度设计的影响，得到以下结论：

(1)传统板下组合静刚度设计方法忽略了铁垫板翘曲变形与板下垫板非线性弹性特征，导致板下组合静刚度设计值与实测值相差较大，并且设计误差随着紧固扭矩的增加而增大。当紧固扭矩分别为150、200、250 N·m时，设计误差为37.8%、55.9%、94.3%，无法满足工程设计精度要求。

(2)采用板下组合结构非线性有限元模型分析时，同时考虑铁垫板翘曲变形与板下垫板非线性弹性因素的共同影响，仿真得到的板下组合静刚度及铁垫板翘曲变形与实测数据基本一致。在设计紧固扭矩为150～250 N·m范围内，板下组合静刚度最大设计误差仅为2.4%，可达到工程设计精度要求。

(3)若仅考虑板下垫板非线性弹性因素，设计结果与传统均匀加载得到的静刚度基本一致，荷载施加方式不会影响设计结果，对板下组合静刚度设计精度的提高几乎没有影响。若仅考虑铁垫板翘曲变形，相比传统设计方法而言，板下组合静刚度设计误差在不同紧固扭矩情况下均明显减小，但仍随紧固扭矩的增加而增大。当紧固扭矩为250 N·m时设计误差为28.3%，同样无法满足工程设计要求。

该设计误差主要由板下垫板非线性弹性因素导致，板下垫板非线性弹性越强，相同紧固扭矩情况下的设计误差越大。

为了准确设计弹性分开式扣件板下组合静刚度，充分反映板下组合结构的真实变形与受力特征，板下组合静刚度的设计必须同时考虑铁垫板翘曲变形与板下垫板非线性弹性因素的综合影响。