基于随机森林偏差校正和多源遥感数据的天然次生林地上生物量估测

赵颖慧，蔡鑫垚，甄 贞

（东北林业大学 a.林学院；b.森林生态系统可持续经营教育部重点实验室，黑龙江 哈尔滨 150040）

森林蓄积量和生物量的精确估测是评估生态系统过程、碳平衡及气候变化的重要基础[1]。森林生物量分为地上生物量（Above ground biomass,AGB）和地下生物量（Below ground biomass,BGB），地上生物量包括树干、树枝和树叶生物量[2]。遥感技术不断地提高能够快速、准确地提取不同尺度的森林参数[3]，使得森林AGB 的高精度估测成为可能。以Landsat为代表的多光谱数据对植被指数的提取越来越精确，而植被指数、不同波段的组合与森林生物量大多呈正相关性[4]。激光雷达（Light Detection and Ranging,LiDAR）对植被垂直结构尤其是林冠下层结构有很强的探测能力，对森林参数的提取和定量反演有一定的优势[5]，但LiDAR 数据缺少对光谱信息的表达，且存在点云穿透性缺失的情况，不能有效地提升反演尺度[6]。因此要进行较大尺度的森林AGB 估算，就要结合LiDAR 数据高精度森林参数的提取和Landsat 光学遥感数据对AGB 的空间拓展[7]。

森林AGB 估测方法有传统的多元回归方法[8]、偏最小二乘回归（Partial least squares regression,PLSR）[9]和逐步回归（Multiple stepwise regression,MSR）[10]等，但传统的预测模型往往存在着区域差异性而难以大范围推广[11]。现阶段，生物量预测模型由传统的统计回归模型向非参数化模型拓展，例如：神经网络（Neural network,NN）[9]、支持向量机（Support vector machine,SVM）[12]、K最邻近法（K-nearest neighbor,KNN）[13]和随机森林（Random forest,RF）[11]等，它们更能揭示森林AGB 与多源遥感数据之间的非线性复杂关系[14]，此外还能降低估测模型中大量预测因子的数据维度[15]。高煜堃[16]基于多源数据的亚热带森林AGB 估测中，在进行特征筛选和最优特征组合后构建的SVM 模型精度较MSR 提升60.2%以上，对AGB 小于40 t·hm-2和大于120 t·hm-2区域的预测精度可以提高14.6%。在森林结构参数的估测中，RF 和BP 神经网络以森林植被指数和纹理因子为特征变量能够保持较高的准确性[17]，同时当有大量共线性强且包含高异常点的数据输入时，RF 模型能保持较好的鲁棒性[18]。但对于森林结构复杂、郁闭度较高的地区，由于光谱信息的饱和导致非参数模型估测精度的降低，因此需要对模型进行改进如参数优化[19]和偏差校正[20-21]等，能有效地提升模型估测精度。

综上所述，结合多源遥感数据进行森林AGB估测已十分常见，但大多数只研究了多源遥感数据在估测中的协同，很少有在郁闭度较高的天然次生林中采用非参数模型及随机森林偏差校正模型进行大尺度估测森林AGB。本研究以东北林业大学帽儿山实验林场为研究区域，结合2015年机载激光雷达（Airborne laser scanning,ALS）数据和2016年Landsat 8 OLI 数据以及森林资源连续清查固定样地复测数据，提取高度、地形信息、植被指数和纹理因子等信息，对特征变量筛选后，使用传统的MSR 和非参数模型（SVM 和RF）对郁闭度较高的天然次生林森林AGB 进行估测及对比分析，之后用随机森林偏差校正（Bias-corrected RF,BCRF）模型进行校正，为较大尺度的森林AGB 估测提供依据。

1 材料与方法

1.1 研究区概况

研究区为东北林业大学帽儿山实验林场（127°29′～127°44′E，45°14′～45°29′N），位于黑龙江省尚志市帽儿山镇境内，场址距市区80 km。林场总面积约26 496 hm2，共10 个施业区，平均海拔为300 m。地处中温带大陆性季风气候影响区，具有典型的温带季风气候特征。本研究样地均属典型的东北东部天然次生林，主要树种包括：落叶松Larix gmelinii、红松Pinus koraiensis、云杉Picea koraiensis、白桦Betula phatyphylla、榆树Ulmus pumila、色木、椴树Tilia amurenisis、水曲柳Fraxinus mandshurica、胡桃楸Juglans mandshurica、黄菠萝Phellodendron amurense、杨树Populus davidiana和柞树Querus mongolica等，研究区域位置及样地分布如图1所示。

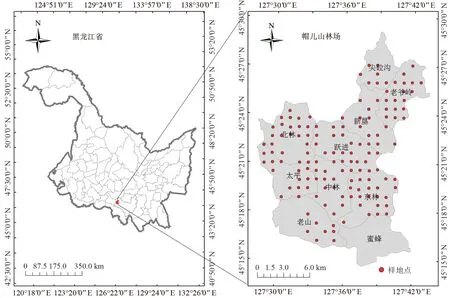
图1 研究区位置和样地分布Fig.1 The location of study area and plot distribution

1.2 研究数据获取

1.2.1 遥感数据

ALS 数据获取于2015年9月，是由中国林业科学研究院的LiCHY 系统搭载的LiDAR 传感器（Riegl LMS-Q680i）进行扫描获取的二级产品。激光传感器发射脉冲最大频率400 kHz，波长为1 550 nm，扫描角度±30°，采样间隔1 ns，垂直精度0.15 m，平均点云密度3.6 点·m-2，旁向重叠度≥60%。

Landsat8 OLI 数据获取于地理空间数据云（http://www.gscloud.cn/），时间为2016年6月24日，OLI 传感器光谱范围覆盖9 个波段，选用其中的2～7 波段，空间分辨率为30 m，辐射分辨率为12 bit，还包括一个15 m 的全色波段，成像宽幅为185 km×185 km。

1.2.2 样地数据

样地数据为2016年森林资源连续清查固定样地复测数据，剔除异常样地点（由于样地点所在的Landsat8 OLI 影像提取的纹理特征变量存在异常值）后使用其中的142 块30 m×20 m 的菱形样地，对样地内胸径DBH（Diameter at breast height）大于5 cm 每木检尺，记录胸径（cm）、树种、郁闭度等。

1.3 数据预处理

ALS 数据预处理包括：首先将点云按样地位置进行切片处理[22]，之后去除离群点和高程异常点[19]后，分为地面点和非地面点；将地面点云数据利用邻近像元内插[23]算法生成数字高程模型（Digital elevation model,DEM）；样地ALS 点云数据减去相应的DEM 值即为样地尺度的归一化点云数据[8]。

Landsat8 OLI 数据预处理包括：辐射定标、大气校正和几何精校正。在进行几何精校正时，利用相对误差较小的21 个同名地物点对Landsat8 OLI 数据进行校正，误差控制在0.1 个像元以内。

1.4 样地AGB 计算

利用东北林区主要树种的生物量可加性模型系统[24]计算地上生物量，分别对树干、树枝和树叶部分的生物量进行估算，相加后得到AGB，如公式（1）所示：

式中：w为生物量；D为胸径；a*、b*为模型参数；ɛ为模型残差；s，b，f，a分别代表树干、树枝、树叶和地上生物量；依据不同的树种参数值不同，详见文献[24]。按树种分别计算样地内每株树的生物量，然后样地内单木生物量之和，与样地面积相除，得到单位面积生物量。

1.5 特征变量提取

1.5.1 ALS 数据特征变量提取

以样地ALS 归一化点云数据提取高度分位数、高度统计变量和地形变量共3 组变量。在LiDAR所有回波中，首回波较稳定[22]，因此本研究从10%到99%每隔10%计算分位数[25]。另外，Shi等[26]研究表明以5%为间隔计算的分位数之间高度相关，故保留以25%为间隔计算的分位数[27]。本研究最后选取13 个分位数变量：H10、H20、H25、H30、H40、H50、H60、H70、H75、H80、H90、H95和H99，这些高度分位数对生物量有极强的解释性[23,28]。

高度统计变量共9 个：最大值（Hmax）、最小值（Hmin）、均值（Hmean）、标准差（Hstd）、峰度（Hkurtosis）、偏斜度（Hskewness）、方差（Hvariance）、众数（Hmode）和变异系数（Hcv）[19]。另外，坡度、坡向可作为AGB 估测的辅助数据[29]，本研究以地面点计算的DEM 数据获得2 个地形变量：坡向（aspect）、坡度（slope）。

最后，以样地ALS 点云提取的13 个高度分位数变量、9 个高度统计变量和2 个地形变量分别取平均，为样地尺度的24 个ALS 特征变量。

1.5.2 Landsat8 OLI 特征变量提取

本研究首先选取预处理后的OLI 数据的2、3、4、5、6、7 波段并进行波段组合，由于原始多光谱影像波段数多，且波段间存在不同程度的相关性，因此选择合适的波段进行组合可以减小数据的冗余性，同时不同波段组合后，会使植被特征更明显[7]，选择表1所示的波段组合；本研究分别计算8 个植被指数作为特征变量，包含：归一化植被指数（Normalized difference vegetation index,NDVI）、土壤调节比值植被指数（Soil adjusted ratio vegetation index,SARVI）、差值植被指数（Difference vegetation index,DVI）、垂直植被指数（Perpendicular vegetation index,PVI）、土壤调节植被指数（Soil adjusted vegetation index,SAVI）、增强植被指数（Enhanced vegetation index,EVI）、修正的土壤调节植被指数（Modified soil adjusted vegetation index，MSAVI）和修正的简单比值植被指数（Modified simple ratio vegetation index,MSR），计算公式见文献[23]。另外，纹理信息是密集的遥感像元的特征显示，往往能够反映森林地上植被的分布情况，在森林AGB 估测过程中纹理信息是极其重要的参数值，因此本研究在提取纹理前对图像进行默认窗口（3×3）的傅里叶变换，之后以灰度共生矩阵（Gray level co-occurrence matrix,GLCM）提取纹理特征[30]：均值（Mean,ME）、方差（Variance,VA）、均匀性（Homogeneity,HO）、对比度（Contrast,CO）、相异性（Dissimilarity,DI）、熵（Entropy,EN）、二阶矩（Second moment,SM）和相关性（Correlation,CR），计算公式见文献[30]。最终，基于Landsat8 OLI 共提取22 个OLI 特征变量，即6 个波段组合、8 个植被指数和8 个纹理信息。

表1 本研究中应用的波段组合计算公式†Table 1 The formula of band combination used in this study

1.6 特征变量筛选

由于光学遥感数据间存在一定的共线性，容易造成研究数据的冗余[31]，而ALS 数据也会因为数据量众多造成特征变量不敏感导致估测精度降低[32]，因此需要进行特征变量筛选。本研究采用逐步回归法（Stepwise）将合适的变量选入模型并剔除引起多重共线性的变量。若自变量使统计量F很小且t检验结果不显著（P＞0.1），将其剔除并进行下一个自变量筛选；若F值较大且t检验达到显著水平（P＜0.05），则该变量进入模型，进入模型的方差膨胀因子（Variance Inflation Factor,VIF）越大多重共线性越强[33]。

1.7 AGB 估测模型的构建

将142 块固定样地的80%（113 块）以筛选后的特征变量因子构建AGB 估算模型，以剩余20%（29 块）样地作为检验数据。在AGB 估测模型研究中，本研究采用的评价指标有：调整决定系数（），均方根误差（RMSE），相对均方根误差（rRMSE）[34]来评价模型预测性能。一般情况下，RMSE 和rRMSE 值越小，模型预测性能越好，具体计算公式详见参考文献[34-35]。

本研究选取的基础模型是多元逐步回归（MSR），它是统计方法中应用最广泛的参数化算法，支持向量机（SVM）和随机森林（RF）是最典型的非参数化回归模型，模型的泛化能力和拟合精度要优于传统的参数模型[7,36]，具体原理此处不再赘述，重点介绍随机森林偏差校正。

随机森林（RF）是从原始样本中有放回的进行多次随机抽样，并对每次抽取的样本以及样本特征变量建立决策树，利用样本特征变量进行判决，综合所有决策树的预测经投票得出最终结果[37]。由于研究中特征变量的重要性程度不同，如果决策树中重要性强的特征变量被无差别的随机抽样就会导致回归结果的偏差，为避免这种情况，可以对RF 模型预测结果进行偏差校正，即随机森林偏差校正（Bias-corrected RF,BCRF）。BCRF 一般可以通过调整残差实现，主要包括内置偏差校正（Bias corrected,BC）和残差旋转偏差校正[21]（Residual rotation,RR）。BC 偏差校正原理是建立简单的线性回归模型，将样本数据中计算的偏差回溯到模型本身完成偏差校正，使预测值更加靠近真实值；RR 偏差校正原理是将带有偏差的趋势线进行旋转，实现数据偏差的减小完成偏差校正，其结果近似于将偏差回溯到预测值本身。Zhang 等[20]研究表明BC 和RR 偏差校正精度相似，RR 偏差校正对数据量大于1 000 以上的数据集校正效果最佳，对数据量较小的数据集选取BC 偏差校正[38]结果更稳定。因此，本研究使用R 软件提供的RF 包中的BC 进行偏差校正。BC 偏差校正是首先需要随机选择一部分RF 模型的预测值Y作为测试集并计算其残差r，建立响应函数如公式（2）所示，然后将RF 模型的预测值代入公式（2）计算得，最后将代入公式（3）得到最终的YBCRF，完成内置偏差校正。

2 结果与分析

2.1 特征变量筛选结果

特征变量筛选（表2）后，ALS 数据保留了4个特征变量：Hskewness（高度偏斜度）、aspect（坡向）、slope（坡度）和H90（90%高度分位数）；Landsat8 OLI 数据保留了2 个特征变量：即SAVI（土壤调节植被指数）和b42（波段4、2 组合）；多源数据（ALS+Landsat8 OLI）保留了7 个变量：CR（相关性）、b547（波段5、4、7 组合）、b53（波段5、3 组合）、Hskewness（偏斜度）、aspect（坡向）、slope（坡度）、H90（90%高度分位数）。

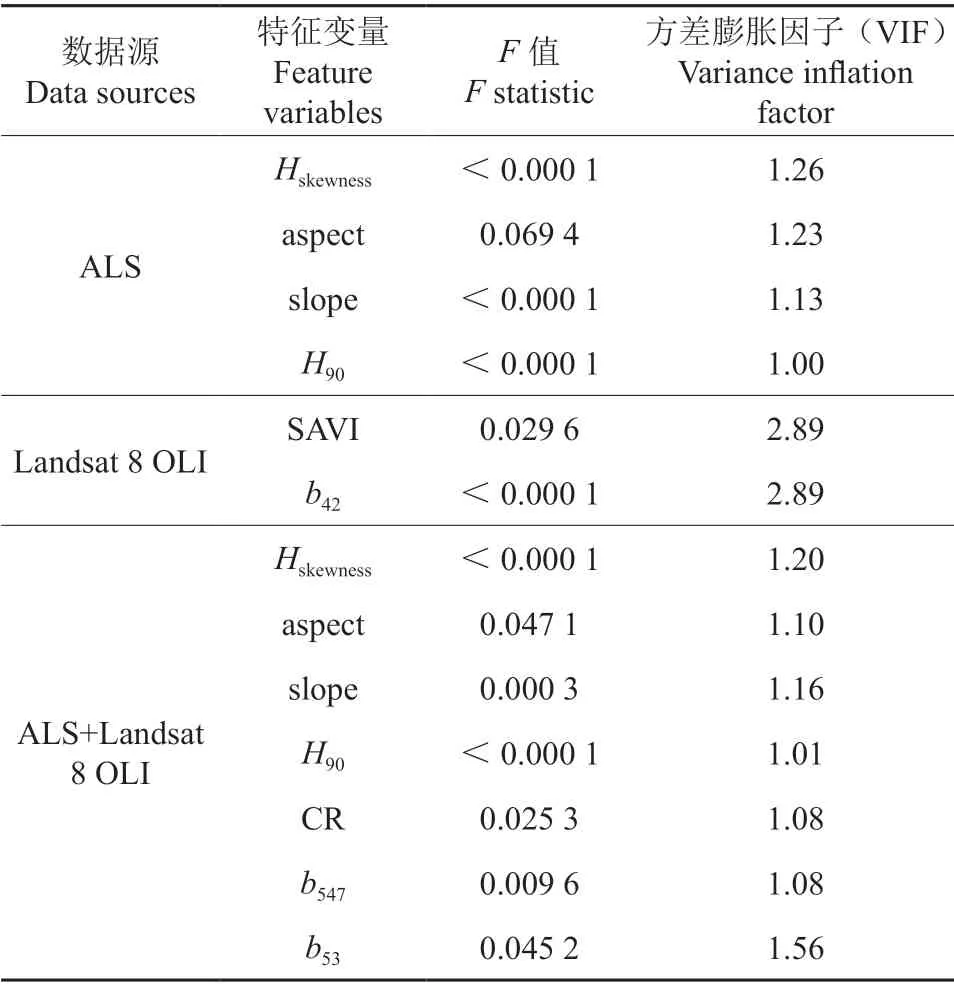
表2 基于不同数据源的特征变量筛选结果†Table 2 The feature selection results based on different data source

2.2 森林AGB 估测模型

以ALS 数据、Landsat8 OLI 数据和多源数据（ALS+Landsat8 OLI）3 种数据源对29 块检验样地分别应用3 种模型（MSR、SVM 和RF）进行森林AGB 预测，并计算相应的RMSE 和rRMSE进行精度评价（表3），对实测生物量和预测生物量建立响应函数（图2）。

表3 基于不同模型的精度评价结果†Table 3 The results of accuracy assessment based on different models

图2 样地实测值与各个模型预测值的关系Fig.2 Relationships of measured and predicted aboveground biomass values with different models

从图2a—c 可以看出，基于MSR 模型，多源数据（ALS+Landsat8 OLI）的AGB 拟合优度要高于应用单一数据源ALS 或Landsat8 OLI 数据源，为0.523 2；从图2d—f 可以看出，基于SVM 模型，多源数据AGB 拟合优度最高，为0.644 5；从图2g—i 可以看出，基于RF 模型，同样是多源数据拟合优度最高，为0.680 1。RMSE 和rRMSE 的结果（表3）定量地证实了这一情况，即基于多源数据的模型预测性能均表现最优，Landsat8 OLI 数据估测精度最低。无论应用哪种数据源，3 种模型（MSR、SVM 和RF）中RF 模型预测性能最优（RMSE 最小达到49.71 t·hm-2，rRMSE 最小达到32.48%），SVM模型次之（RMSE 最小达到52.80 t·hm-2，rRMSE最小达到35.28%），MSR 模型估测精度最低（RMSE 最小达到57.29 t·hm-2，rRMSE 最小达到43.26%）。从估测值和实测值的线性回归图可以看出，无论使用哪一种数据和回归模型，都会出现比较明显的AGB 估测低值偏高、高值偏低的现象，因此对估测精度最高的多源遥感数据+RF 模型进行RF 偏差校正。

2.3 RF 偏差校正结果

以多源遥感数据（ALS+ Landsat8 OLI），采用RF 偏差校正后精度如图3所示。从图2i 和图3可以看出，RF 模型进行偏差校正后的预测精度有一定的提升，模型的拟合精度提高了12%以上（由0.68 提高到0.77），预测结果更加接近1∶1 趋势线；表征模型内部稳定性[33]的RMSE 由49.71 t·hm-2减小到43.26 t·hm-2，rRMSE 由32.48%减小到21.84%，减小了10.64%。因此，引入偏差校正后模型预测性能提升显著，BCRF 模型预测稳定性得到提高。

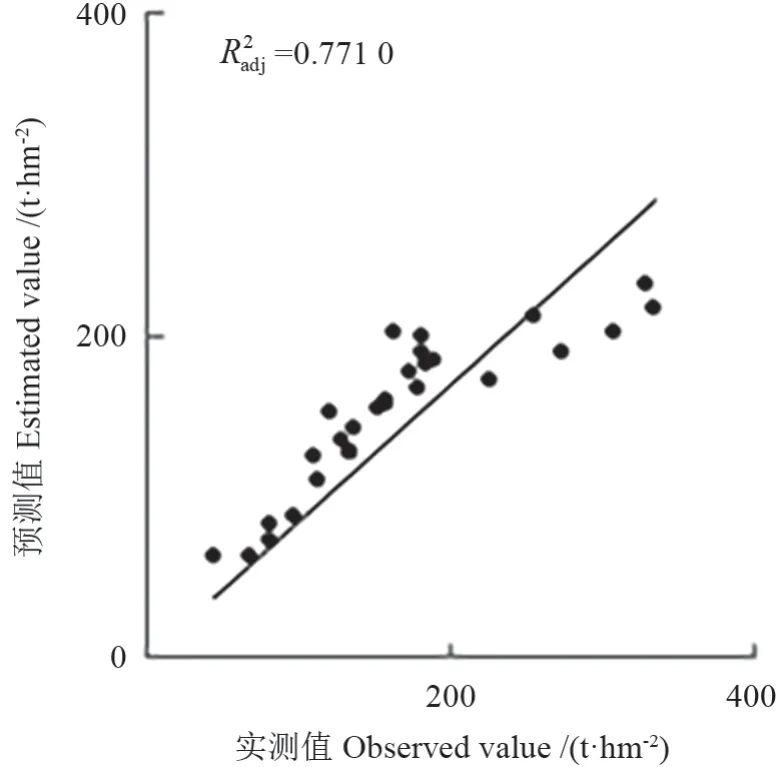
图3 样地实测值与BCRF 预测值关系Fig.3 Relationships of measured and estimated AGB using BCRF

将RF 和BCRF 的残差进行对比，结果如图4所示。由图4可以看出，偏差校正后的模型残差呈下降趋势，尤其在RF 模型残差较大和预测生物量值小于100 t·hm-2范围时残差下降程度较大，在此范围内偏差校正对模型的改进效果最佳，在其他生物量范围内，改进效果不明显。因此BCRF模型的偏差校正效果与生物量值大小有关。

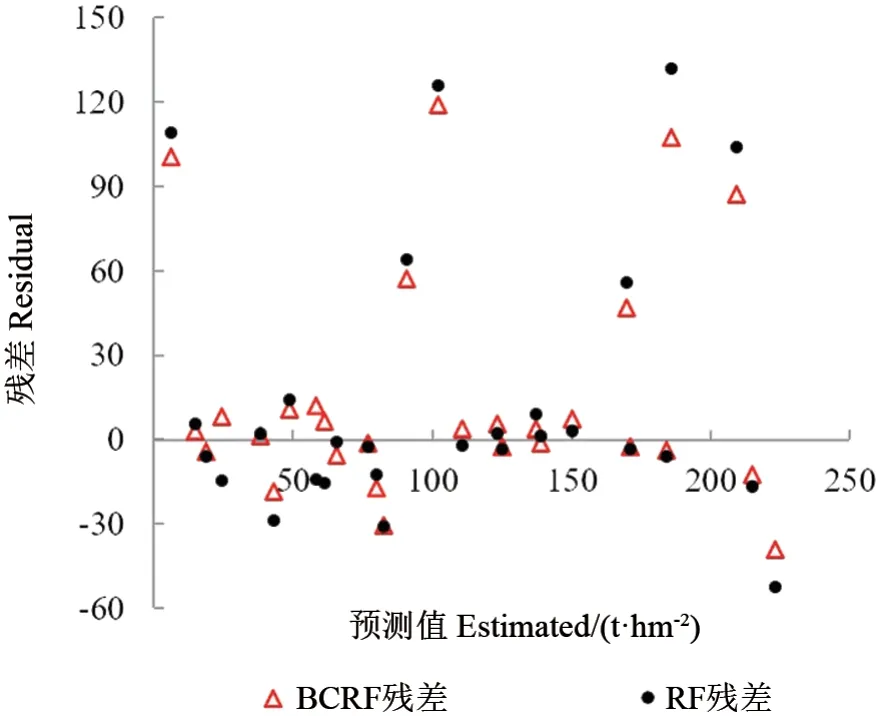
图4 RF 模型与BCRF 模型残差对比Fig.4 Comparison of residuals between RF and BCRF

2.4 森林AGB 估测值分段精度评价

上述结果分析了基于不同数据源和模型算法的总体精度，但是无法提供不同AGB 范围影响下的模型预测性能。故以多源遥感数据（ALS+Landsat8 OLI）的4 种估测模型（MSR、SVM、RF 和BCRF），分别计算RMSE 和rRMSE，并对森林AGB 估测值进行分段精度评价，结果如图5所示：

由图5a—b 可以看出，估测模型性能在不同的AGB 范围存在差异性，但RMSE 和rRMSE 所反映的趋势大体相同。当AGB 在100～200 t·hm-2范围时，模型（MSR、SVM、RF 和BCRF）中的RMSE 和rRMSE 是最小的，模型对生物量的估测精度最佳；当AGB 大于200 t·hm-2范围时，模型的估测精度最差（RMSE 和rRMSE 最大）。

图5 4 种估测模型在不同AGB 范围内的RMSE 和rRMSE 统计Fig.5 Comparison of four models on RMSE and rRMSE in different AGB ranges

当AGB 小 于100 t·hm-2时，4个模型RMSE和rRMSE 的排序为：BCRF＜RF＜SVM＜MSR，排序越靠前RMSE 和rRMSE 越小，模型的预测精度也最高；BCRF 的rRMSE 从MSR 的59.92%减小到30.63%，模型性能提升最为显著。在AGB处于100～200 t·hm-2，预测性能最佳的是BCRF模型（RMSE=13.72 t·hm-2，rRMSE=8.69%），最差的是MSR 模型（RMSE=48.87 t·hm-2，rRMSE=28.15%）；在AGB 大于200 t·hm-2范围内，RMSE 的排序为：BCRF＜RF＜MSR＜SVM，BCRF 的RMSE=70.13 t·hm-2，rRMSE=34.58%，相较于SVM 模型，分别减小19.21 t·hm-2和12.93%。综上可得，无论是总体还是分段计算的RMSE 或rRMSE，BCRF 模型对AGB 的估测精度明显优于其他模型的精度，表现为有较低的RMSE 和rRMSE；尤其在100～200 t·hm-2的AGB 范围内，BCRF 模型对估测精度的改进是显著的，同时看到，SVM 模型（RMSE=23.55 t·hm-2，rRMSE=16.13%）相较于MSR 模型，RMSE 减小25.32 t·hm-2，rRMSE 减小12.02%；RF 模型（RMSE=16.42t·hm-2，rRMSE=10.36%）相较于MSR 模型，RMSE 减小32.45 t·hm-2，rRMSE 减小17.79%，可见非参数模型对估测精度的改进程度在此范围内是显著的；在AGB 小于100 t·hm-2和大于200 t·hm-2范围内，非参数模型的RMSE 或rRMSE（除BCRF 模型外）也较MSR 变小，减小量均在10.0%以下。

对比RF 模型和BCRF 模型，发现偏差校正对预测模型性能提升是明显的。当AGB 小于100 t·hm-2时，RMSE 由57.27 t·hm-2（RF 模型）减小到了29.61 t·hm-2（BCRF 模型），rRMSE由41.62% 下降到30.63%；当AGB 处在100～200 t·hm-2范围内时，RMSE 由16.42 t·hm-2（RF 模型）减小到13.72 t·hm-2（BCRF 模型），rRMSE由10.36%下降到8.69%；当AGB 大于200 t·hm-2时，RMSE 由77.56 t·hm-2（RF 模型）减小到70.13 t·hm-2（BCRF 模型），rRMSE 由36.80%减小到34.58%。模型性能提升最明显的是AGB 小于100 t·hm-2的区间内，对预测精度的改进效果为其他区间的5 倍以上，BCRF 模型明显地提升了AGB 小于100 t·hm-2范围内的生物量估测精度。结合图4的残差可以看出，在AGB 小于100 t·hm-2范围内，BCRF 模型通过将修正的残差弥补到预测值上实现了预测精度的提升，有效地解决了AGB估测中出现的小值偏大现象。

3 结论与讨论

3.1 讨 论

3.1.1 多源数据在AGB 估测中的协同作用

单独使用ALS 或Landsat8 OLI 数据对森林AGB 的估测精度是有限的，尤其在郁闭度和生物量较高的天然次生林地区，Landsat8 OLI数据容易产生光谱饱和现象，AGB 估测精度欠佳。ALS 数据的引入可提高AGB 估测的精度。从表3和图2可以看出，基于MSR模型，多源数据（ALS+Landsat8 OLI）（=0.52,RMSE=57.29 t·hm-2,rRMSE=43.26%）的结合较单独使用ALS 数据（=0.47,RMSE=61.25 t·hm-2,rRMSE=45.79%）拟合优度提高了10.6%，模型预测性能提升2.5%，较单独使用Landsat8 OLI 数据（=0.19,RMSE=76.75 t·hm-2,rRMSE=50.82%）拟合优度提高了173.7%，预测性能提升7.6%；基于SVM 模型，多源数据（ALS+Landsat8 OLI）（=0.64,RMSE=52.80 t·hm-2,rRMSE=35.28%）的结合较单独使用ALS 数据（=0.53,RMSE=57.36 t·hm-2,rRMSE=37.86%）拟合优度提高了20.8%，模型预测性能提升2.6%；较单独使用Landsat8 OLI 数据（=0.16,RMSE=71.76 t·hm-2,rRMSE=50.58%）拟合优度提高了300.0%，预测性能提升15.3%；基于RF 模型，多源数据（ALS+Landsat8 OLI）（=0.68，RMSE=49.71 t·hm-2,rRMSE=32.48%）的结合较单独使用ALS 数据（=0.64,RMSE=52.58 t·hm-2,rRMSE=34.25%）拟合优度提高了6.3%，预测性能提升1.8%，较单独使用Landsat8 OLI 数据（=0.21,RMSE=69.46 t·hm-2,rRMSE=47.26%）拟合优度提高了223.8%，模型预测精确度提高了14.8%。Laurin 等[39]利用ALS 和高光谱数据对非洲热带森林进行AGB 估测，当与多源数据结合时，估测精度均提高20.0%以上，这与本文研究结果相似。本研究中，使用Landsat8 OLI 数据进行AGB 估测时，拟合优度仅为0.19，rRMSE为50.82%，在两种遥感数据中表现最差。探究原因如下，除因为光谱饱和现象导致的估测精度偏低的原因外，由于Landsat8 OLI 数据分辨率（30 m×30 m）与样地大小（20 m×30 m）不匹配也是另一方面原因。在数据预处理阶段对Landsat8 OLI数据已进行焦点统计，通过邻域计算减小误差。但尺度不匹配问题始终存在，产生的混合像元导致植被指数和纹理因子等特征变量与样地实测信息存在匹配误差，一定程度上降低了AGB 估测精度。在之后的研究中，希望找到合适的方法解决尺度不匹配的问题，提升光学遥感数据对AGB 的估测精度。综上，以多源遥感数据结合的方式提升森林AGB 的估测精度是可行的。

3.1.2 基于不同模型的AGB 估算

基于多源数据（ALS+Landsat8 OLI），RF和SVM 模型对AGB 的估测精度均优于MSR 模型，拟合优度提高了30.0%，rRMSE 减小了10.78%，模型预测性能得到提升。与传统统计回归模型相比，非参数模型更适合AGB 估测，能够揭示与数据维度有关的非线性问题，这与Tian 等[40]的研究结果一致。另外，基于多源数据RF 模型精度高于SVM 模型，RMSE 减少3.09 t·hm-2，rRMSE 减小2.8%。探究原因如下，RF 的一个主要优点是自举采样和变量抽样，其中所有变量子集都是随机选择的，使用标准回归树的每个节点进行最佳分割。在这种情况下，由于对输入变量的变化相对不敏感，RF 模型可以降低算法的过拟合和多重共线性风险，从而提高了算法对预测数据的泛化性和鲁棒性，这与Wang 等[18]的研究结果相似。RF 算法适合于多变量大样本的数据集，以其本身抽样随机性实现多变量预测；SVM 算法适合小样本少变量甚至有缺失数据的数据集[41-42]，利用在高维空间中变量稳定的拓扑关系实现多变量拟合，但是本研究为了将非参数模型（SVM、RF 和BCRF）与基础模型（MSR）相比较，对特征进行了筛选和统一，结果发现RF 模型仍然有较大的优势。

基于多源数据，不同的估测模型对森林AGB预测值的RMSE 分布在43.26～57.29 t·hm-2之间，同时所有的估测模型针对不同的AGB 范围其模型性能也各不相同。当AGB 小于100 t·hm-2时，SVM、RF 和BCRF 模型相较于MSR 模型的RMSE 均有所降低，且rRMSE 平均减小20.5%，模型预测性能提升20.5%；当AGB 范围在100～200 t·hm-2时，SVM、RF 和BCRF 模型相较于MSR 模型的RMSE 平均减小30.97 t·hm-2，且rRMSE 平均减小16.42%，模型预测性能提升16.4%；当AGB 大于200 t·hm-2时，MSR、RF 和BCRF 模型相较于SVM 模型的RMSE 平均减小12.71 t·hm-2，rRMSE 平均减小9.47%，预测性能提升9.5%。因此，以RF 和BCRF 模型为代表的非参数模型在AGB 处于100～200 t·hm-2范围时估测精度的提升效果是最佳的，其模型的性能和稳定性表现最优。在AGB 小于100 t·hm-2和大于200 t·hm-2时，RF 和SVM 模型提升估测精度效果不佳，没有解决小值高估和大值低估的现象。探究原因如下，研究中需要一定量样本对机器学习模型进行训练，但是由于生物量估测饱和现象的普遍存在，导致当训练样本没有足够的代表性时，机器学习语言会将饱和现象也作为训练学习的本领，最终导致此现象无法显著消除[43]。研究结果与高煜堃[16]研究结果相似，即RF等非参数模型对森林AGB 较低（小于100 t·hm-2）或较高（大于200 t·hm-2）的区域不敏感。因此，BCRF、RF 与SVM 等非参数模型对森林AGB 预测精度在AGB 处于100～200 t·hm-2范围内最佳，在其余范围有一定的限制。

3.1.3 RF 模型偏差校正在AGB 估测中的优势

BCRF 模型通过调整残差实现了预测精度的提高，将初始RF 模型的由0.68 提高到0.77。特别地，当AGB 范围在小于100 t·hm-2时，BCRF 模型比RF 模型的RMSE 降低27.66 t·hm-2，rRMSE 减小10.99%。在其他范围内，rRMSE 平均降低1.95%，因此BCRF 模型在AGB 范围在小于100 t·hm-2时估测精度是最佳的，且模型稳定性最强。在一定程度上削弱了蒙诗栎等[30]研究中出现的生物量估测的饱和现象，使模型在AGB 小于100 t·hm-2范围内估测值偏大的误差降低11.0%，研究结果与Jongwoo 等[21]对RF 回归模型的偏差校正结果一致。但研究中，对于大于200 t·hm-2范围的AGB 低估现象依然无法显著削弱，探究原因如下，内置的BC 模型对残差偏大的值进行修正时，收敛性较弱。在本研究的基础上，需要进一步讨论和解决光谱信息、纹理因子的变量效能，探讨RF 模型偏差校正的完善性。

3.2 结 论

本研究使用ALS 数据和多光谱Landsat8 OLI数据，探究两种数据源在对天然次生林AGB 估测中的协同作用，以及非参数模型（SVM、RF 和BCRF）对AGB 的估测潜力和适用性。研究结果表明：两种数据源的结合能够明显提高AGB 的拟合优度（比使用ALS 数据提升6.3%以上，比使用Landsat8 OLI 数据提升219.7%以上）；在3种模型（MSR、SVM 和RF）中，RF 的拟合能力最好，模型精度最佳，相较于MSR 模型RMSE 减小7.58 t·hm-2，rRMSE 减小10.78%；相较于SVM 模型RMSE 减小3.09 t·hm-2，rRMSE 减小2.8%；RF 偏差校正模型（BCRF）相较于RF 模型，RMSE 减小6.45 t·hm-2，rRMSE 减小10.64%。

BCRF 模型的使用总体上可以提升AGB 估测精度，在AGB 处于100～200 t·hm-2范围最佳，尤其在AGB 小于100 t·hm-2时，相较于RF 模型，RMSE 减小27.66 t·hm-2，rRMSE 减小10.99%，可以有效地削弱AGB 估测中的小值高估现象，预测性能提升11.0%，为精确探测生物量分布阈值提供了可行方法，也为东北林区AGB 的精准估算提供了技术支持。