基于直觉模糊集和亮度增强的医学图像融合
2021-07-30张林发张榆锋李支尧
张林发,张榆锋*,王 琨,李支尧
(1.云南大学信息学院,昆明 650500;2.昆明医科大学第三附属医院超声科,昆明 650118)
0 引言
不同的医学成像技术能提供组织或器官的互补信息,如核磁共振图像(Magnetic Resonance Imaging,MRI)检测人体内部软组织,正电子发射断层成像(Positron Emission computed Tomography,PET)、单光子发射计算机断层成像(Single-Photon Emission Computed Tomography,SPECT)获取器官的代谢信息,用于肿瘤或血管疾病检测[1]。在医疗实践中,由于医生需要对多模态医学图像进行分别观察,从而导致疾病诊断准确度和效率的降低。医学图像融合技术可以将多模态图像中的相关信息结合起来,有助于疾病的诊断和治疗[2]。
图像融合方法中像素级融合因图像失真度最小而应用最为广泛[3]。像素级融合方法可以分为两类:空间域和变换域[4]。前者由于直接在空域处理图像导致融合效果较差[5-6](如文献[6]中对图像进行明度、色调、饱和度(Intensity,Hue,Saturation;IHS)变换,而IHS 变换容易造成频谱失真),因此后者成为研究热点[7]。基于变换域图像分析工具的图像融合方法可以分为三个过程:图像分解、系数融合和图像重构。变换域的方法如图像金字塔等[8-11]。多尺度变换(Multi-Scale Transforms,MST)也是经典的变换域方法,能够弥补图像金字塔不具有方向性的缺点,吸引了许多学者的注意,如小波变换[12]、轮廓波变换[13]、剪切波变换[14]。其他MST 方法如局部拉普拉斯滤波器(Local Laplacian Filter,LLF),LLF 在医学图像融合应用也是经过三个过程,如文献[15]中应用LLF 进行图像分解,然后在高频和低频分别采用兴趣区和区域能量最大的融合策略。和MST 相比,多尺度几何变换(Multi-scale Geometric trAnsform,MGA)是MST 的改进方法,具有平移不变性,融合图像不会出现伪Gibbs 效应。MGA 主要包括非下采样轮廓波变换(Non-Subsampled Contourlet Transform,NSCT)和非下采样剪切波变换(Non-Subsampled Shearlet Transform,NSST)。文献[16]中首先通过NSCT将源图像分解成高频和低频子带,然后分别对其采用基于二型模糊逻辑和区域特征的融合策略;文献[17]中提出了基于视觉特征和NSCT的融合方法。但NSCT运算耗时较多,因此NSST成为基于MGA 融合方法的主流。文献[18]中提出了使用结构张量和NSST 分别取提取图像细节信息和几何特征的医学图像融合方法;文献[19]中提出了结合NSST 和ripplet变换的融合方法,高频子带采用基于改进拉普拉斯的融合策略,低频子带基于空间频率进行融合。图像分析工具是融合策略有效性的基础,而提高变换域方法融合质量的关键是融合策略的设计[20]。近年来,脉冲耦合神经网络(Pulse Coupled Neural Network,PCNN)被广泛应用于高频或低频子带的处理[21-24]。如文献[24]中提出使用NSCT 分解源图像,低频采用最大选择策略,高频采用尖峰皮质模型进行医学图像融合。但基于PCNN 的融合方法效果依赖于手动设置的参数,自适应程度较低[25]。稀疏表示(Spare Representation,SR)和MGA 类似,不同在于MGA 使用固定原子,而SR 通过基于目标数据集预先建立完备字典去表示图像。基于SR的融合方法首先获得稀疏系数,然后对稀疏系数进行融合[26-28]。为了进一步提高融合图像质量,SR 和MST 结合的方法被提出,如文献[29]中提出先对图像多尺度变换,然后对低频子带采用基于SR的融合策略。然而由于获取稀疏系数的过程使用匹配追踪类算法,往往时间复杂度较高。为了获得更多特征应用于融合,文献[30]中提出将尺度不变特征变换应用于提取图像局部细节信息。文献[31]中首先对图像进行两层分解,利用引导滤波提取尺度信息对细节层进行融合。近年来,直觉模糊集理论能够处理不确定性问题被应用于图像处理[32-35]。文献[33]中提出了基于分数阶导数和直觉模糊集理论的多聚焦图像融合。文献[35]中首先使用二维经验模态分解替代NSST 中非下采样金字塔对红外和可见光图像进行分解,然后提出基于模糊集理论的融合策略,取得了较好的效果。
传统融合方法通过融合策略设计来同时解决两个关键问题,即细节提取和能量保存[7-31],容易出现源图像信息失真或结果图像能量保存不足等问题。鉴于此,本文提出了一种基于直觉模糊集和亮度增强的融合方法。和传统方法不同在于,该方法分别解决细节提取和能量保存问题:首先使用NSST 分解源图像得到低频和高频子带,其次对于低频子带和高频子带设计不同的策略进行融合,然后通过NSST逆变换得到中间结果图像,最后针对中间结果图像进行亮度增强得到融合图像。实验结果表明,和传统融合方法相比,无论是客观评价还是主观评价,本文方法都能够获得更好的效果。
1 基本理论
1.1 非下采用剪切波变换
剪切波变换(Shearlet Transform,ST)[36]利用仿射系统得到,对于连续小波,合成膨胀的二维仿射系统定义为:

其中:ψ∈L2(R2);A表示膨胀矩阵;S是剪切矩阵,且|detS|=1;k和j分别是方向和尺度参数。对于任意f∈L2(R2),MAS(φ)都可以构成一个紧支撑框架。式(1)中Aj和MST 相关联,Sk与区域面积恒定的几何变换关联。这种特殊的结构使人们可以构造基元素在各个尺度各个方向的紧支撑框架,从而使ST具备了方向敏感性,提高了对奇异信号的表现能力[37]。
但ST 不具有平移不变性,针对这个问题,NSST 将剪切滤波器从伪极化网络映射到笛卡儿坐标系[37],从而摒弃了下采样操作,实现平移不变性,过程如图1 所示,包括非下采样金字塔滤波器组(Non-Subsampled Pyramid Filter Bank,NSPFB)和剪切波滤波器组(Shearlet Filter Bank,SFB)。

图1 NSST分解过程Fig.1 Process of NSST decomposition
1.2 模糊熵
模糊熵是模糊集理论的重要内容,也是对信号概率分布的一种测度[38]。信号中频率组成越复杂,模糊熵越大,表示信号包含的信息越丰富。
设论域X={x1,x2,…,xn},则模糊熵通过以下步骤得到:
1)对X截取窗口长度设定为m,步长为1,则可产生N-m+1个子序列,不同序列之间的距离通过dij=max|xi+k(t)-xj+k(t)|(k=0,1,…,m-1)计算得到,且i≠j,最后可以得到由dij构成的列表矩阵Q。
2)为了减少运算量,统计列表矩阵Q每一行大于阈值F=0.01 的个数占总数N-m+1 的比例,第q行比例记为Cq,当Cq为0 时则将q行舍弃处理。依据式(2)计算得到Φ,式中P为剩余行数。

其中:D是距离d的模糊隶属度,通过式(3)得到,式(3)中n和r分别是D的梯度和宽度。

3)通过式(4)得到模糊熵。

2 融合方法
本文方法由信息提取部分和能量保存两部分组成,如图2所示。

图2 本文融合方法框架Fig.2 Framework of the proposed fusion method
2.1 基于直觉模糊集理论的图像融合
本部分方法以已完成配准图像为前提。以MRI和PET融合为例,IM表示MRI 图像,IP表示PET 图像,实现过程如图3所示,其中除源图像以外的灰度图像做了伪彩色处理。主要步骤为:

图3 本文图像融合流程Fig.3 Flowchart of the proposed image fusion method
1)NSST 分解:对规格为N×N输入图像IM和输入图像IP进行L层NSST 分解,每层分解方向数矩阵K(l)(l∈[1,L])。分别得到低频和高频子带,即NSSTM={LM,}和NSSTP={LP,},其中LM和分别是输入图像IM的低频子带和第L层第K个方向高频子带。
2)低频子带融合:利用区域能量和方向能量的模糊熵来融合从而得到融合图像低频子带。
3)高频子带融合:分别对输入图像IM和输入图像IP进行IHS 变换,使用明度分量的区域能量引导非隶属度函数的确定,最后得到融合图像高频子带。
4)NSST 重构:分别对第2)和第3)步的结果低频子带和高频子带做NSST逆变换,得到图像R。
2.1.1 低频融合过程
图像经过NSST分解后,能量主要集中在低频子带。通过保存低频子带的能量,能够更好地保存源图像的信息。在医学图像融合中,只使用区域能量(Local Energy,LE)无法充分捕获源图像特征[33]。本文提出结合区域能量和方向能量(Direction Energy,DE)的模糊熵来设计融合策略。
区域能量定义见式(5):
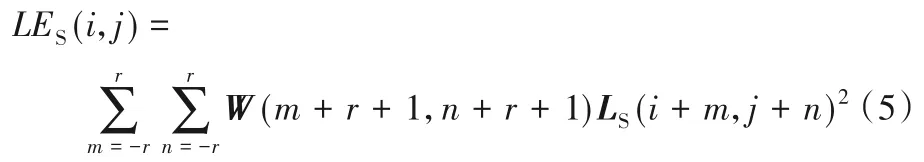
其中S ∈{M,P},W是加权矩阵。W的计算公式为:

方向能量采用sobel 算子在水平和竖直两个方向提取图像,定义如下:

其中:⊗表示卷积操作;Si(i=1,2)表示不同方向的sobel 滤波器,定义见式(8)、(9)。

在PET图像纯色信息分布区域或MRI的图像空间轮廓分布区域会出现区域能量和方向能量的急剧变化,从而导致融合过程互补信息的丢失。为了避免这种情况发生,对方向能量使用本文1.2 节中的理论求得模糊熵ENTS,如果模糊熵越大说明所包含的信息越丰富,基于LES和DES的ENTS来融合图像的低频子带,通过式(10)得到,式中A(i,j)是关于源图像IM和IP的低频子带的函数。

2.1.2 高频融合过程
在社会生产及科学研究中,非此即彼的二值逻辑无法对模糊概念进行描述。直觉模糊集(Intuitionistic Fuzzy Set,IFS)理论[39]能够较好地描述模糊关系,直觉模糊集A定义如式(11)所示,式中X是非空集合。

此外,对于X中的每个模糊子集,有三个概念对其进行描述,除了非隶属度函数γA和隶属度函数μA(两者的关系见式(12)),还有直觉指数πA(x)描述对象属于直觉模糊集的反对程度,可以衡量x对A的犹豫程度,定义见式(13)。

直觉模糊集理论已在其他图像融合应用场景(如多聚焦图像融合、可见光和红外图像融合)成功应用[33-35]。在医学图像融合中,高频子带包含病理图像的边缘、纹理等信息[2],融合高频对于保存源图像的细节信息具有重要作用。而高频子带中某一像素隶属于MRI图像或PET图像的程度是一个不确定性问题,本文将直觉模糊集理论用于这一问题的处理。隶属函数的确定是直觉模糊集理论的核心,传统的优先关系定序法中优先关系依赖于手动设置[39]。
鉴于此,针对医学图像融合的特点,本文提出一种改进的基于优先关系定序法的隶属度函数确定方法。该方法的核心在于基于源图像的亮度分量的区域能量来确定优先关系,从而确定保留源图像信息的优先关系,有利于诊断信息的提取。
改进的基于优先关系定序法的IFS 隶属度函数确定算法步骤如下:
步骤1 输入n个对象μ1,μ2,…,μn。
步骤2 确定优先关系矩阵C=(cij)n×m,其中cij∈[0,1]表示ui相对于uj的优越程度。特殊地,当cij=0,cji=1 时表示ui比uj没有任何优越程度。本文提出基于图像亮度分量的区域能量来确定。
首先利用式(14)~(17)对图像进行IHS变换[6]。
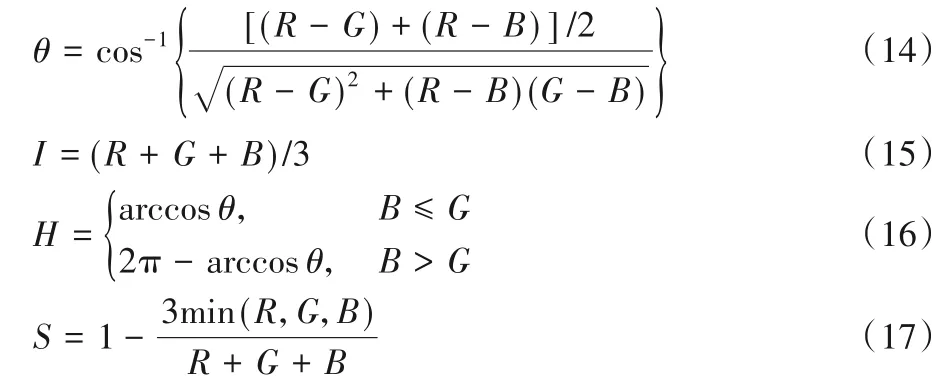
然后对亮度分量I利用式(5)、(6)计算得到LEIS,并进一步依据LEIS利用式(18)、(19)来确定优先关系矩阵。

2.2 基于柯西函数的图像亮度增强
由于2.1 节中得到的融合图像光谱信息及其互补信息保持度较高,但是亮度不足,视觉上表现较暗。为此,需要一种不改变图像色调信息为前提,仅改变亮度的方法,从而达到能量保存的目的。
难点在于,如果单一调整图像的RGB 任一通道,会导致光谱信息失真。因此,本文提出一种基于柯西函数的图像亮度信息增强方法,步骤如下:
1)对2.1 节中得到的图像R进行色调、饱和度和明度(Hue,Saturation,Value,HSV)变换[40],如式(24)~(27),得到色调分量H、饱和度分量S、明度分量V。H取值范围是0°~360°,取值范围内三等分处对应光谱色红绿蓝,例如H(i,j)为120°表示图像在像素(i,j)处光谱色为绿色。S和V取值范围是0~1,S数值越接近1,表示越接近光谱色;V表示光谱色明亮程度,数值越大说明光谱色反射比越大。


2)为了保持光谱信息不变,不对色调分量H进行调整,只改变饱和度分量S、明度分量V。构建柯西函数γ,见式(28),其中p为γ的调整参数,取值范围为0~2;τ、ℓ 分别为饱和度分量S、明度分量V的调整参数;函数υ定义见式(29),变量IRS和IRV定义分别见式(30)、(31)。

3)通过式(32)求解柯西函数γ的L-2最大范数,得到τ、ℓ。然后依据τ、ℓ调整饱和度分量S、明度分量V,如式(33)、(34),能够引起RGB 数值增大,从而改变亮度分量(结合式(24)~(27)、(15)可知)。
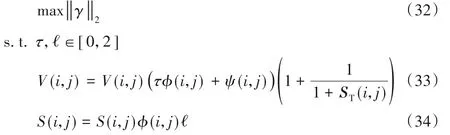
4)最后使用HSV逆变换得到融合结果图像F。
为获得p的最优取值,将结构相似度(Structural SIMilarity,SSIM)[41]作为图像亮度增强效果评价指标,定义如式(35),式中uM为2.1 节中得到的融合图像(下称源图像)的均值,uF为亮度增强后得到的图像(下称增强图像)的均值,稳定系数C1=6.502 5,C2=58.522 5。在p取值范围内,增强效果和p是凸函数关系,见图4,并在p=1处取得最优值。
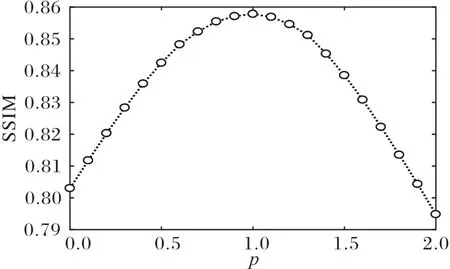
图4 不同p值时源图像和增强图像SSIM曲线Fig.4 SSIM of source image and enhanced image with different p values

为了进一步验证增强效果及p取值为1的优越性,使用15组图像(每组包含源图像及增强图像)从色调分量、饱和度分量、亮度提升效果三个方面进行实验验证。
色调分量是对图像纯色属性的直接描述,决定光谱波长。当p=1 时,通过式(36)得到源图像的区域能量分布,式中HO表示源图像的色调分量。同理得到其余图像的区域能量分布,15组图像的色调分量区域能量分布见图5,可知图像亮度增强前后色调分量没有发生变化。

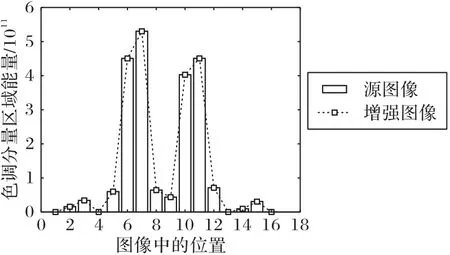
图5 源图像和增强图像色调分量区域能量对比Fig.5 Local energy comparison of hue component between source image and enhanced image
取不同p值,实验图像的饱和度区域能量分布见图6,当p=1时对源图像曲线的依从性最好。

图6 不同p值时增强图像和源图像饱和度区域能量对比Fig.6 Local energy comparison of saturation between source image and enhanced image with different p values
亮度提升效果验证过程为首先对每组图像进行IHS 变换得到亮度分量;然后使用式(37)得到亮度提升百分比,式中IO和IE分别为源图像和增强图像的亮度分量,m为IO中非零像素的个数;最后同理得到不同p值不同图像的亮度提升百分比,如图7 所示。由实验结果可知,p=1、p=1.1、p=1.2 时亮度平均提升66.44%、63.70%、61.08%。
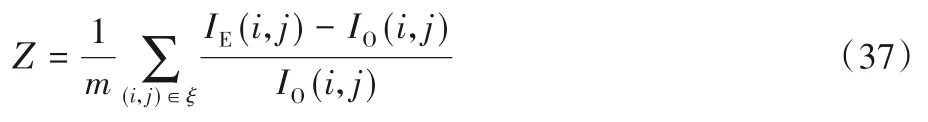
由图7 中可知亮度增强方法在不同图像中亮度增强百分比波动较大。结合式(15),亮度的改变本质上是调整彩色图像的RGB 分量,而像素点光谱通过RGB 分量的比例混合来决定。由于在同等视觉效果下,不同颜色需要的亮度增强百分比不同,所以亮度增强效果的波动和图像不同颜色区域构成比例直接相关。
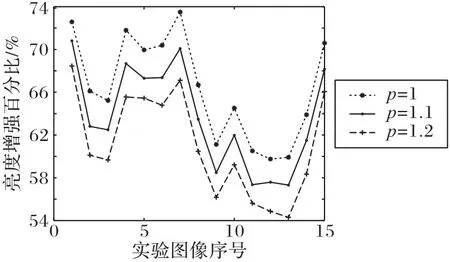
图7 不同p值时亮度增强百分比Fig.7 Percentage of intensity enhancement with different p values
为了验证结论,首先选取6 组图像(每组图像包含源图像及增强图像)进行实验,源图像及对应增强图像如图8 所示。然后由于MRI 图像和PET 图像融合结果图像主要区域为四种:无光谱信息区域、黄色区域、蓝色区域、红色区域,分别对图8 中每张源图像选取四个实验区域,并放大四倍放置在左上角(对应无光谱信息区域)、右上角(对应黄色区域)、左下角(对应蓝色区域)和右下角(对应红色区域)。

图8 实验图像及选取的颜色区域Fig.8 Experimental images and selected color areas
最后同样使用式(37)进行计算得到不同图像所选取的实验区域亮度增强百分比,如图9 所示,四个实验区域平均亮度增强百分比分别为89.88%、54.86%、46.82%、25.52%。
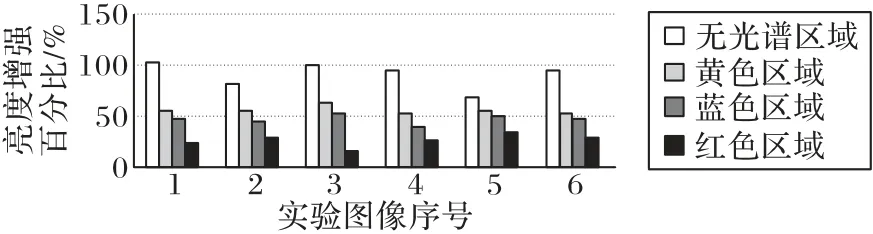
图9 不同图像不同区域亮度增强百分比Fig.9 Percentage of intensity enhancement in different areas of different images
综上所述,本文提出的亮度增强方法在参数最优时,能够在不改变图像光谱信息及对比度情况下有效地改变图像亮度,且由于不同图像特征不同,会使亮度增强百分比在合理范围内波动。
3 实验与结果分析
为评估本文方法的图像融合效果,使用18 组不同病理状态的MRI 和PET 图像、25 组MRI 和SPECT 图像进行融合实验(数据集地址为:http://www.med.harvard.edu/AANLIB/),图像规格为256×256,且已完成图像配准。将本文方法(代码见https://github.com/bananatreelookbajiao/medical-image-fusion)和基于传统框架的图像融合方法进行对比,包括:GF[31]、NSCT[24]、NSST[19]、DWTDE[12]、DFIFT-EF[30]、IHS-PCA[6]、MSTSR[29]和LLF-IOI等方法[15],所对比方法的参数均依据对应论文进行设置。本文方法中NSST 分解层数L=4,每层分解方向数矩阵K=[8,8,16,16],亮度增强方法中p=1。实验环境为Intel Core CPU i5-8250U @ 1.6 GHz,内存8 GB,操作系统Windows 10(64 bit),编程软件为Matlab R2017a。
3.1 视觉质量
图10~13 是18 组MRI 和PET 图像融合结果中4 组不同病理形态的融合结果,而图14~17 是25 组MRI 和SPECT 图像融合结果中4 组不同病理形态的融合结果,其中Proposed-1 和Proposed-2 都是由本文方法得到的图像,Proposed-1 表示未经亮度增强方法处理的图像。GF 和MST-SR 方法无法提取MRI图像的纹理信息,同时还出现亮度不足的问题;NSST、DWTDE 和DFIFT-EF方法得到的图像光谱信息严重失真或丢失;NSCT对于轮廓信息和光谱信息都不能保存;LLF-IOI方法存在较大的噪声干扰,无法在临床中为医生提供准确的诊断信息;和本文方法相比,IHS-PCA 方法在图9 中能量保持度不足,在图10~17 中将源于PET 图像的功能信息丢失。由此可知,本文方法在细节信息提取、能量保存等方面表现最好,具有最好的视觉对比度。
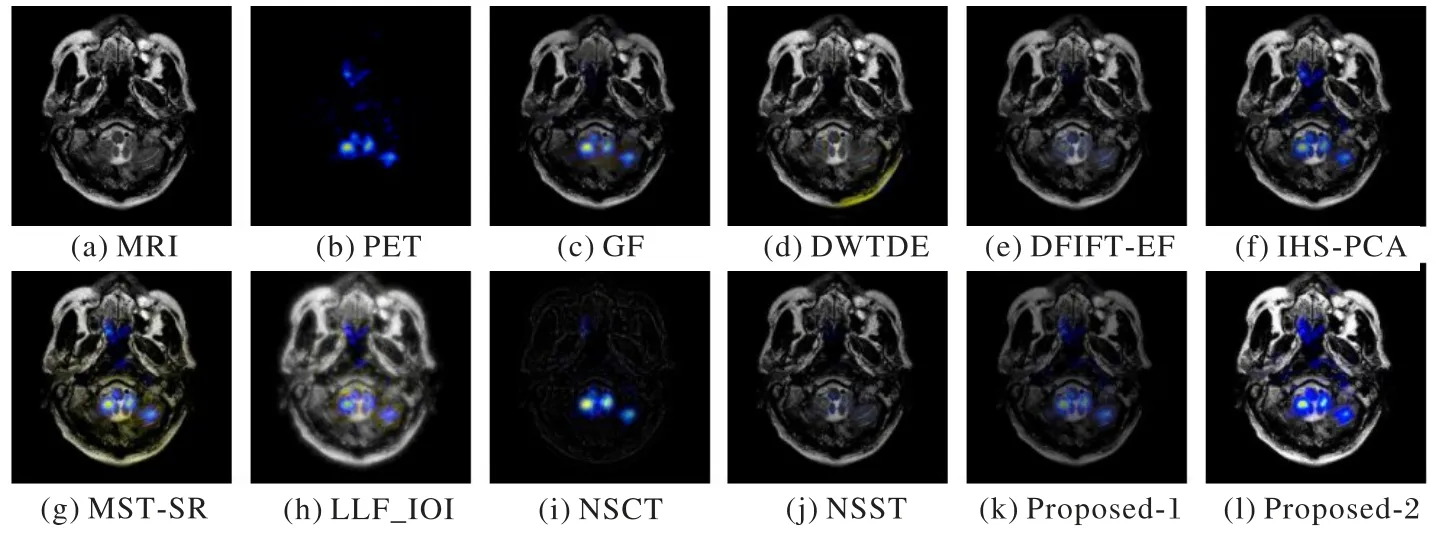
图10 第一组MRI和PET图像融合结果Fig.10 The first group of MRI and PET image fusion results

图11 第二组MRI和PET图像融合结果Fig.11 The second group of MRI and PET image fusion results

图12 第三组MRI和PET图像融合结果Fig.12 The third group of of MRI and PET image fusion results

图13 第四组MRI和PET图像融合结果Fig.13 The fourth group of of MRI and PET image fusion results
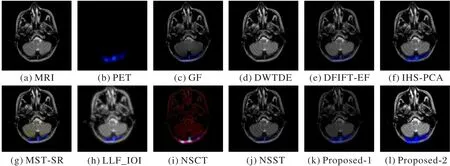
图14 第一组MRI和SPECT图像融合结果Fig.14 The first group of of MRI and SPECT image fusion results

图15 第二组MRI和SPECT图像融合结果Fig.15 The second group of MRI and SPECT image fusion results
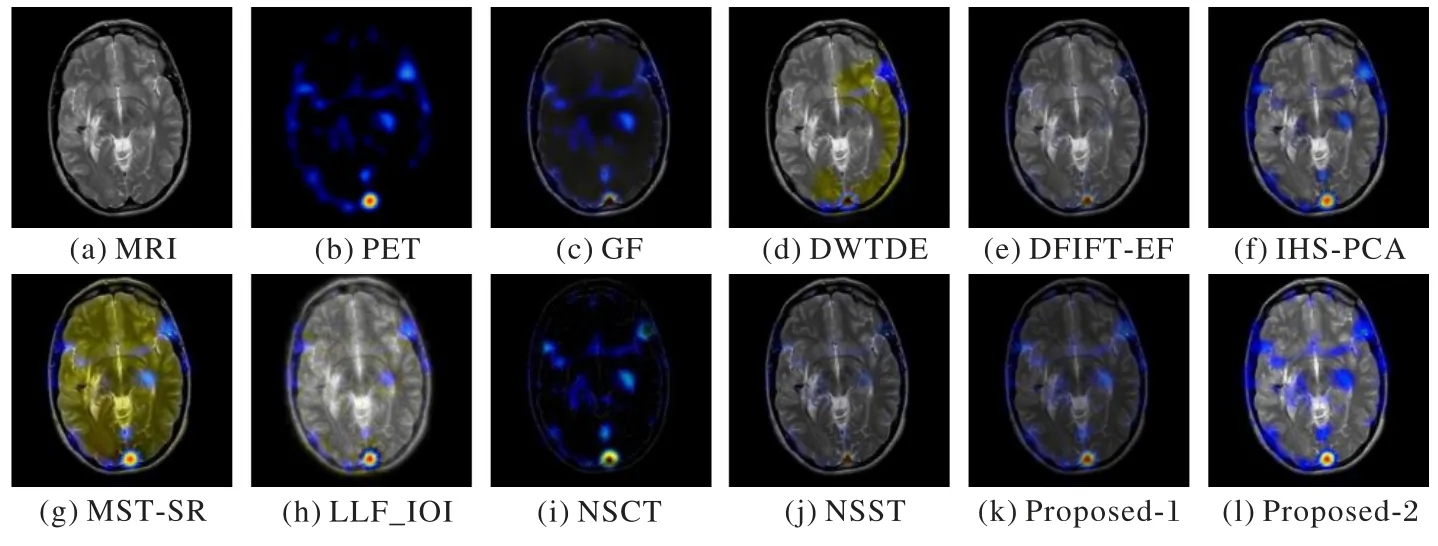
图16 第三组MRI和SPECT图像融合结果Fig.16 The third group of MRI and SPECT image fusion results
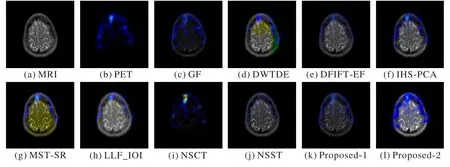
图17 第四组MRI和SPECT图像融合结果Fig.17 The fourth group of MRI and SPECT image fusion results
此外,为了尽可能展示本文的融合效果,分别选取MRI和PET、MRI 和SPECT 图像融合结果各6 组,置于图18 和图19中,每组图像源图像置于上方,增强图像放置于下方。

图18 本文方法对部分MRI和PET图像融合结果Fig.18 Fusion results of some MRI and PET images by using the proposed method
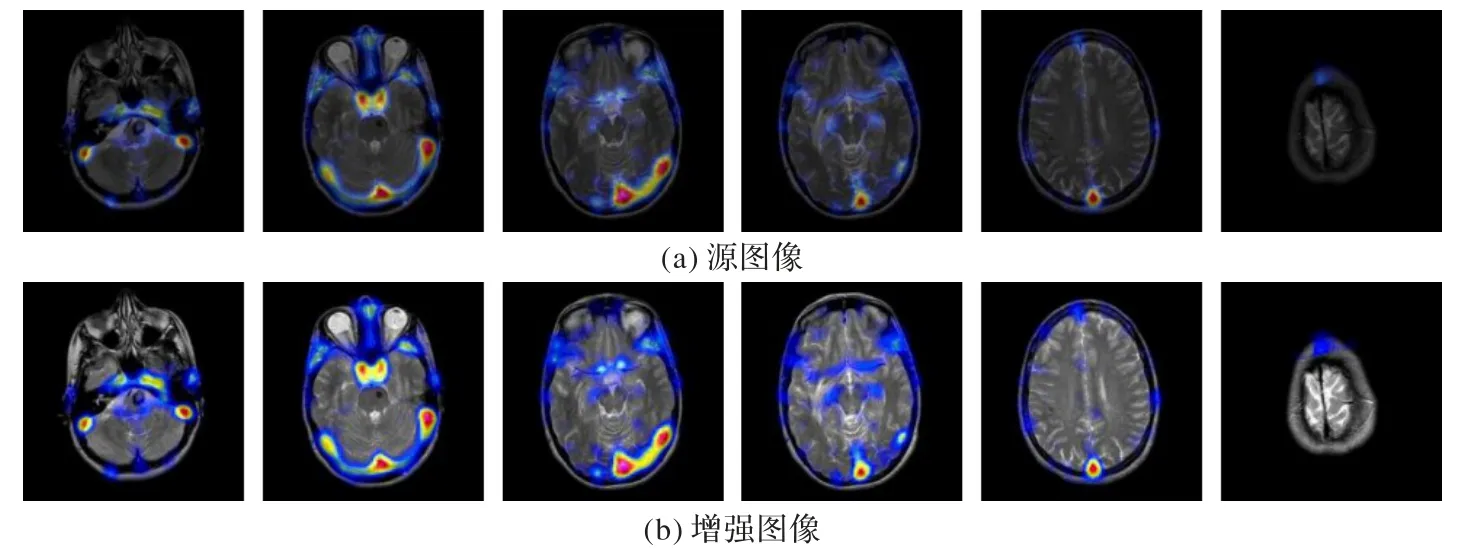
图19 本文方法对部分MRI和SPECT图像融合结果Fig.19 Fusion results of some MRI and SPECT images by using the proposed method
3.2 客观评价
使用以下五个客观评价指标对不同方法的融合结果进行分析,这五个指标数值越大,表示质量越好。
标准差(Standard Deviation,SD)计算方式如下:

互信息(Mutual Information,MI)[42]计算公式如下,其中MIM,F、MIP,F分别表示IM和F、IP和F互信息:

空间频率(Spatial Frequency,SF)[1]由空间行频率RF和空间列频率CF组成:
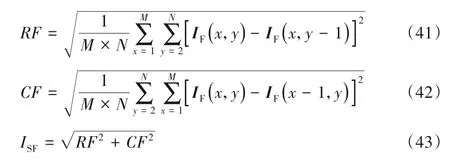
Piella评价指标Q[1]基于结构相似度和对比度来评价融合图像质量,计算公式如下:
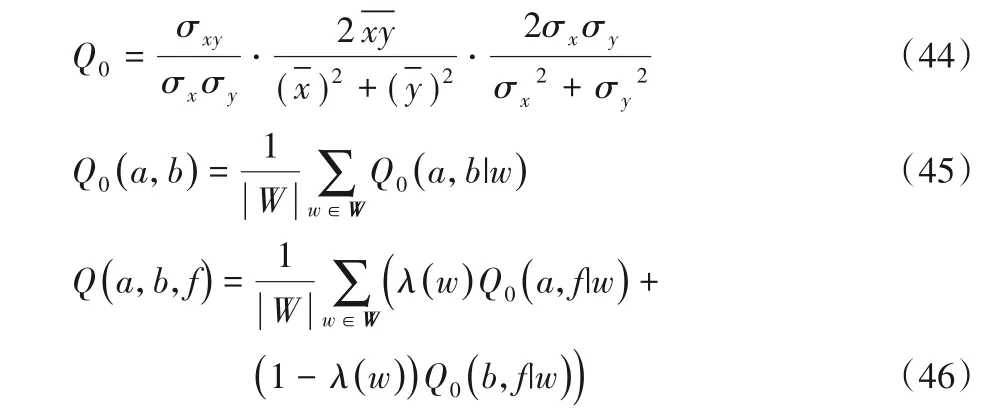
平均梯度(Average Gradient,AG)[42]定义为:
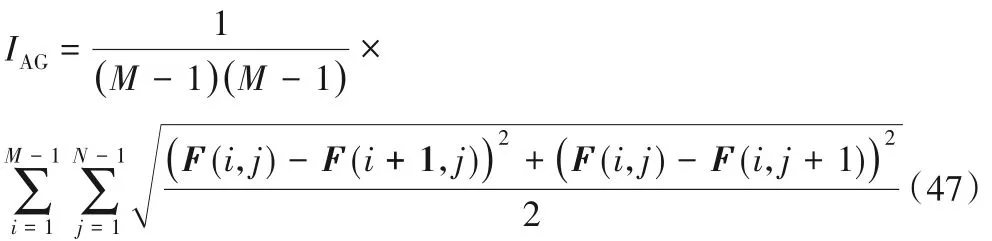
信息熵EI(Entropy of Information,EI)[1]表达式为:

MI能够衡量结果图像中来自源图像的信息量;SF用于反映融合图像灰度变化快慢程度;Q 可以描述图像的视觉对比度;AG用来检测图像的清晰程度;EI可以表征图像灰度分布的空间特征,评价图像信息的丰富程度;SD可以反映融合图像整体对比度。表1是18组MRI和PET图像和25组MRI和SPECT图像使用不同融合方法的客观评价指标均值。和其他8 种传统方法相比,在MRI 和PET 图像融合实验中,除了SD,本文方法在其他五个客观评价指标均具有优势,在MRI 和SPECT 图像融合实验中,本文方法在MI、SF、AG和EI等四个客观评价指标优于对比方法。综合客观评价指标所代表的含义,本文方法能够更好地提取MRI图像的空间结构、软组织、纹理等信息,同时可以提高PET或SPECT图像的光谱信息保持度。由于PET/SPECT图像通过光谱来反映诊断信息,所以本文方法的对于融合效果的提升对于临床诊断具有重要意义。

表1 不同融合方法下的客观评价指标均值对比Tab.1 Comparison of mean values of objective indicators under different fusion methods
4 结语
本文工作主要体现在三个方面:1)提出了一种医学图像融合框架,和传统框架不同,该框架分成两部分来分别处理图像融合中两个关键问题(细节提取和能量保存)。2)基于本文提出的融合框架,提出了一种针对医学图像的融合方法。3)提出了一种图像亮度增强方法,通过15 组图像的实验结果表明,该方法在最优参数情况下能够将能量不足的源图像亮度平均提升66.44%,从而得到较好视觉效果的结果图像,且不改变源图像的光谱信息分布。最后使用43 组不同形态不同类型的医学图像进行融合实验,从实验结果可知,和基于传统框架的融合方法相比,本文方法视觉质量最好,同时在六个客观评价指标上均都具有明显优势,验证了本文框架的优越性。
