基于协同进化的约束多目标优化算法
2021-07-30张祥飞鲁宇明张平生
张祥飞,鲁宇明,张平生
(南昌航空大学航空制造工程学院,南昌 330063)
0 引言
在实际工程应用中,很多优化问题在优化多个目标的同时还需要处理各种类型的约束,这类问题被称为约束多目标优化问题(Constrained Multi-objective Optimization Problem,CMOP)。早在十几年前,研究人员针对CMOP 求解已经提出了以无约束的多目标优化方法加约束处理技术的求解方法[1-3]。随着科技的发展,实际工程应用中的要求也随之提高,使用以往的方法已经难以满足实际使用需求,因此各种新型约束多目标优化算法被陆续提出。文献[4]中提出了一种多阶段的优化方法,在不同的阶段采取不同的优化方法;文献[5]中提出了一种推拉搜索框架,将求解过程分成推拉两个搜索阶段,采用多阶段的算法一般具有较快的收敛速度。
由于协同进化算法在求解大规模、高维度和动态优化问题时取得了良好的效果[6-8],近些年部分研究人员开始运用协同进化的思想求解CMOP,并取得了良好的效果。文献[9]中设立了面向收敛的存档和面向多样性的存档两个种群,面向收敛的存档同时优化约束和目标,面向多样性的存档仅优化目标,两个种群在交配选择和环境选择相互合作;文献[10]中将CMOP 分解成约束单目标优化问题,对每个约束单目标优化问题设置独立的种群进行演化,同时设置了一个用于收集其他子种群中非劣解的子种群,基于协同进化的算法往往可以获取良好的结果。
以上两种类型约束多目标优化算法虽然具有各自的优势,但也存在一定的不足。例如文献[4-5]中提出的算法虽然具有良好的收敛速度,但高度依赖决定搜索阶段切换的参数大小选取;文献[9]中算法在高维CMOP 上的平衡收敛性和多样性具有良好表现,但是在低维优化问题上表现一般。文献[11]中从MOEA/D 内在机制及约束处理技术的适应性上展开研究,提出了一种权重向量和个体间的重新匹配策略实现对多样性和收敛性的兼顾。本文借鉴文献[11]的研究思路,从多阶段和协同进化两种优化方式的互补性展开研究,提出基于协同进化的约束多目标优化算法,通过融合多阶段和协同进化这两种优化方式,具有良好的收敛性能,同时能够较好地兼顾多样性和收敛性。
1 相关研究
1.1 CMOP及其相关定义
不失一般性,一个CMOP表达如式(1)所示:

式中:x是一个D维的决策变量;Ω表示决策空间;F(x)由n个实值目标函数组成的目标空间;l和q分别表示不等式和等式约束的数量。
通常情况下,等式约束都会转化成不等式约束的形式,如式(2)所示:
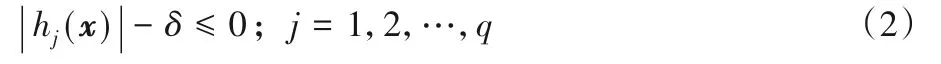
其中:δ为等式约束的容忍参数,一般设定为0.000 1。
决策变量x的约束违反程度如式(3)所示:

定义1 可行解。决策变量x当且仅当G(x)=0时,决策变量x为可行解,否则决策变量x为不可行解。
定义2 Pareto 支配。决策变量xuPareto 支配决策变量xv,记为xu≺xv,当且仅当:
1)∀i∈{1,2,…,m}满足fi(xu)≤fi(xv);
2)∃j∈{1,2,…,m}满足fj(xu)<fj(xv)。
定义3 Pareto 最优解。决策变量xu作为Pareto 最优解,当且仅当决策变量xu在整个目标集中为非支配解。
定义4 理想点(ideal point)。理想点z*可表示为z*=(i=1,2,…,n),决策变量x为可行解。
定义5 极值点(nadir point)。极值点znad可表示为znad=,决策变量x为Pareto最优解。
1.2 约束处理技术
近二十几年以来,针对单目标优化问题已经有很多约束处理技术被提出,主要有可行性准则、罚函数法、ε 约束处理法和多目标优化法等[12]。但这些约束处理技术一般不能直接运用于求解CMOP,虽然它们通过拓展或修改可以运用于求解CMOP,但这类方法具有很大的局限性,在处理低可行域、强约束和不连续帕累托前沿等类型问题时难以取得良好的效果。
在求解CMOP 上,主要有多阶段和协同进化两种优化方式。多阶段优化方式一般是将优化过程划分为多个阶段,不同的阶段采用不同的约束处理技术或优化不同的对象,如文献[4-5]中通过多阶段的形式实现了多种约束处理技术的优势互补。协同进化是指多个对象通过一定的机制和策略开展协同搜索的进化技术,比如多种群、多算法、多操作和多策略集成式进化[13],这类方法大多采取多种群或多种约束处理技术集成式进化。文献[14-15]中通过多种群的形式集成了多种约束处理技术,不同的种群采用不同的约束处理技术,然后通过种群之间的各种交互方式实现信息共享,有效地发挥了多种约束处理技术优势。
2 基于协同进化的约束多目标优化算法
考虑从可行解的搜索阶段和协同进化阶段入手设计本算法。
1)第一阶段,创建多个子种群的稳态演化方法,保证在演化初始阶段可以获取一批高质量可行解,同时保持种群的多样性;
2)第二阶段,基于可行性准则和指定的子种群规模,将种群中的个体分成两个子种群,并对两个子种群分别采用网格约束分解和加权转化单目标的方法引导两个子种群的进化,分别负责算法的多样性和收敛性。
综上所述,给出本文算法的主要步骤:
步骤1 初始化规模为N1+N2的种群P。
步骤2 若种群P中可行解数量小于N1,执行第一阶段演化方法;否则,在种群P中选择N1个可行解为子种群P1,子种群P2=P-P1,执行第二阶段演化方法,合并两个子种群。
步骤3 若满足算法停止条件,则输出种群中的可行解;否则,转步骤2。
2.1 稳态演化方法
由于约束数量、形式及数学特性等方面的影响,一个约束优化问题的可行域可能会非常小或离散,这往往会导致求解该问题的算法收敛效果不佳,甚至无法收敛的情况发生。对于一个约束多目标优化问题来讲,在优化多个目标的同时需要处理约束问题,因此在进行多目标优化之前,为配合协同进化,我们需要获取一个拥有一定数量可行解且具有良好多样性的种群。因此,本文提出了一种稳态的演化方法。差分进化[16]因其简单和有效的搜索能力而受到广泛使用,所以稳态演化选用差分进化作为该方法的搜索引擎。差分进化主要由变异、交叉和选择组成,其中一般常使用的变异算子如式(4)~(6)所示:

其中:xr1、xr2和xr3是三个相互不同的个体;xbest是种群中最好的个体;F是变异因子。
交叉算子主要在目标向量xi和变异向量vi当中生成实验向量ui=(ui,1,ui,2,…,ui,D),二项式交叉算子如式(7)所示:

其中:randj是在[0,1]区间的随机数;jrand是{1,2,…,D}中随机的一个整数;CR是交叉因子。
图1 展示了稳态演化方法的框架:首先将种群随机地划分为m个子种群,然后以式(6)、(7)进行变异和交叉操作,得出相应子种群的后代,在每个子种群之间使用约束支配准则(Constrained Dominance Principle,CDP)[1]更新筛选父本与子代,得到一个新的子种群,最后这些新的子种群集成新的种群P。该方法的目的在于保持种群多样性的同时寻找到高质量的可行解。
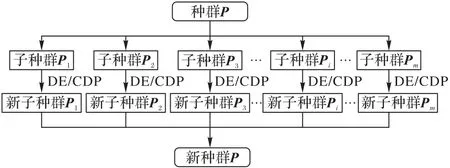
图1 稳态演化结构Fig.1 Steady-state evolution structure
2.2 协同进化策略
在协同进化部分,考虑到CMOP 的Pareto 前沿可能具有各种形状,例如凸或凹型、连续或不连续等,为了可以更好地维持种群的多样性,进而获取完整的Pareto 前沿,本文采用一种基于网格的约束分解方法维持种群的多样性。相较于当前常用的权值求和、切比雪夫和基于惩罚的边界交叉(Penaltybased Boundary Intersection,PBI)分解的方法,该方法利用网格系统维持种群的多样性,在Pareto 前沿为凹型时更具优势,有助于提升算法的普适性。基于网格的约束分解和加权的方法被分别运用于优化两个子种群P1和P2,以达到同时兼顾多样性和收敛性的目的,并结合一定的交互机制实现两个子种群之间的信息共享,进而实现两个子种群之间的协同进化。
2.2.1 基于网格的约束分解
基于网格约束分解的方法由文献[17]针对多目标优化问题(Multi-objective Optimization Problem,MOP)提出,并结合基于分解的排序和字典排序选择进入下一代的解,该方法能够较好维持进化过程中种群的多样性。因此,本文引用文献[17]的演化方法运用于子种群P1的演化。其中,基于网格的约束分解方法具体介绍如下:
1)网格系统的设置。
首先,各个目标根据理想点和极值点之间区间划分为K个子区间,则每个子区间的间隔宽度可以定义如式(8)所示:

对于可行解x的第j个目标所在的子区间计算如式(9)所示:
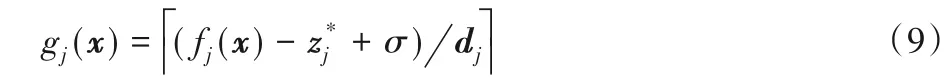
2)约束分解的定义。
约束分解的定义以网格系统为基础,其中第l个目标上的第k个子问题定义如式(9)所示:
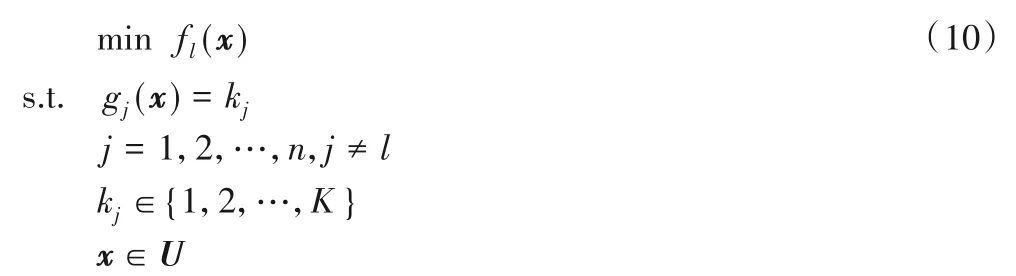
其中:K是一项决定子区间(网格)数量的参数;U表示决策空间中的可行域。
通过将每个目标均匀分成K个区间,把多目标优化问题分解成n×Kn-1个子问题。其中,第l个目标的第k个子问题所包含的解集定义如式(11)所示:
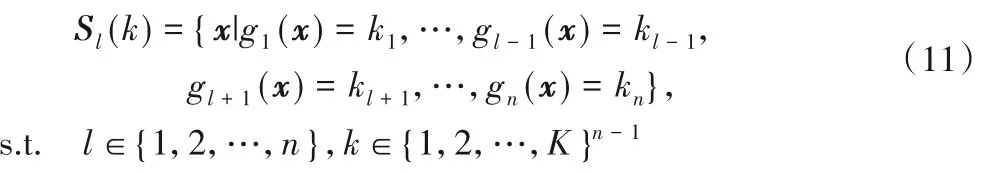
3)基于排序的选择方法。
基于排序的选择方法主要由基于分解的排序和字典排序组成,主要用于选择进入下一代演化的个体。以上部分介绍了约束分解的子问题,每个解集Sl(k)都包含一个解集,基于分解的排序主要对于每个解集Sl(k)按式(11)进行排序,因此每个解都具有n个排序值,然后通过字典排序选择前N1个解作为下一代的父本种群。如图2和表1所示,该问题为网格参数K=4 时的双目标优化问题,经过基于分解的排序后,每个解的排序值如表1 第二列所示(括号前数字为排序值),第三列前7个解为字典排序后选择的解(标注√)。
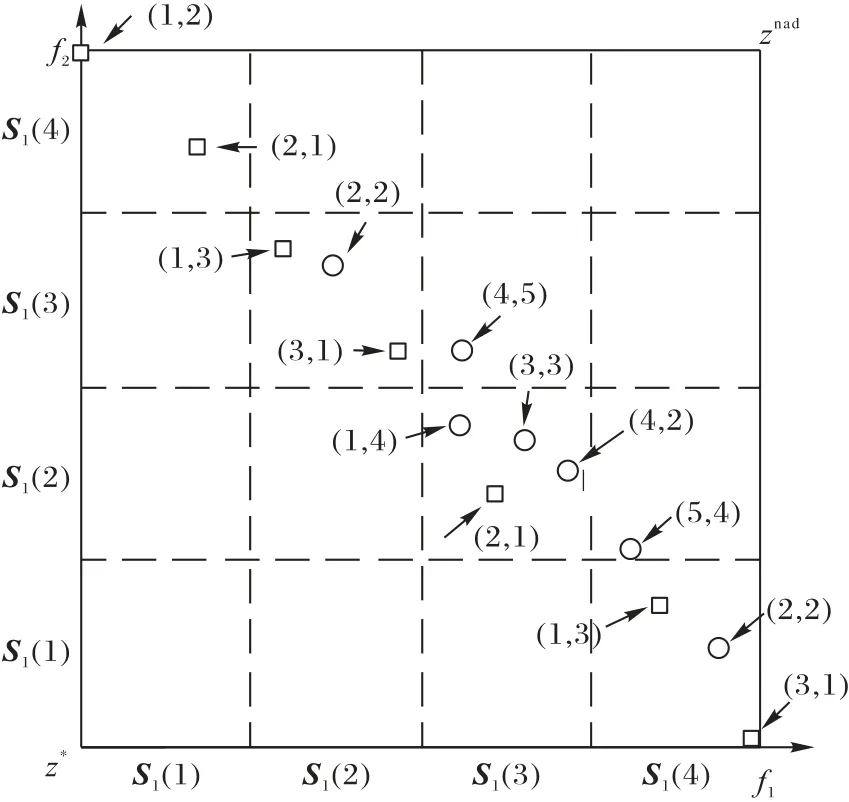
图2 双目标优化问题在网格系统中所有解的排序Fig.2 Ranking of all solutions of bi-objective optimization problem in grid system
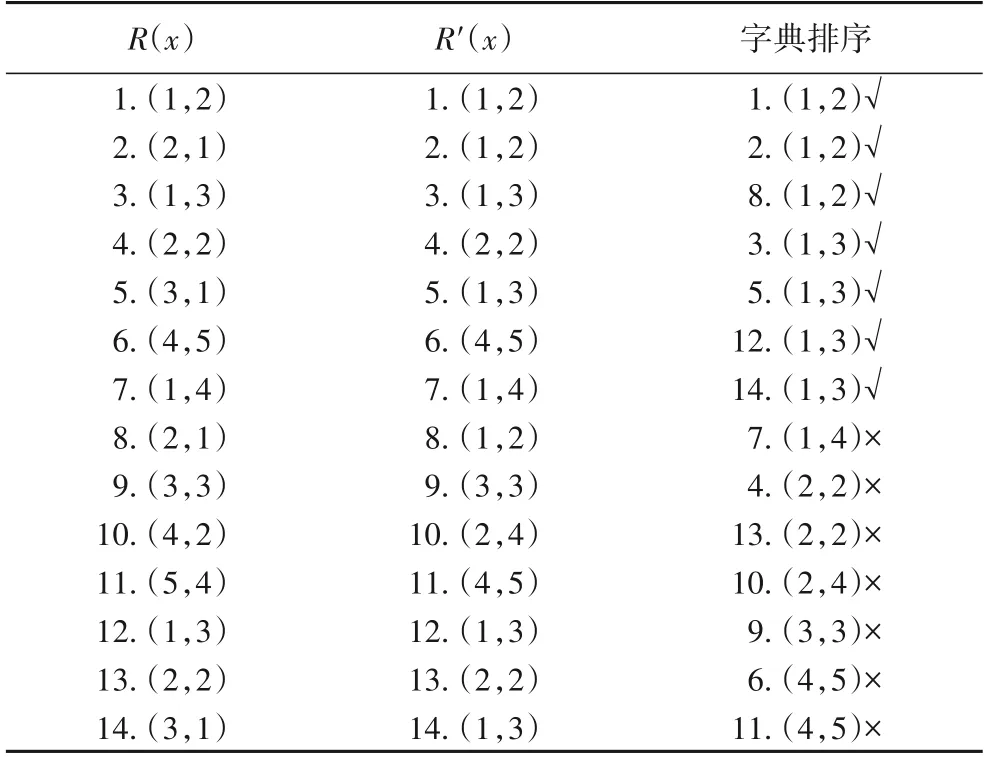
表1 K=4时基于分解的排序和字典排序的过程Tab.1 Procedures of decomposition-based ranking and lexicographic sorting when K=4
2.2.2 加权转化方法
求解CMOP 最终目的是为了获取Pareto 前沿,虽然通过加权的方式将CMOP 转化成约束单目标优化问题仅仅只能获取该问题Pareto 前沿中的某一个解,但该方式可以显著地提高算法的收敛性能。设置合适的权值既可以保持算法具有良好的收敛性又能尽可能地搜索到Pareto前沿的中部位置。
在权值的设置上,文献[4]中提出了一种特殊的加权方式将CMOP 转化为约束单目标优化问题,该方法显著地提升了算法的收敛能力。在子种群P2的演化过程中,为提升算法整体收敛能力,同样也采用类似的加权方法将CMOP 转化成约束单目标优化问题来处理,并采用式(5)的变异方式和基于可行性准则的约束处理技术对子种群P2进行演化。其中,加权方法如式(12)所示:

2.2.3 交互机制
在协同进化过程中,通过种群间的有效交互方式实现信息共享,可以显著地改善算法的求解效果。本文基于可行性准则及设定的子种群规模将种群P划分为两个子种群P1和P2,并分别采用基于网格的约束分解和加权的方式进行演化。在2.2.1 节中,我们采用文献[17]的演化方式对子种群P1进行演化,虽然该方法可以较好地维持种群的多样性,但在约束优化问题中,这种基于网格的演化方法难以跳出不可行域,进而会导致算法无法收敛。为解决该问题,在子种群P2的变异方式中,随机地选择子种群P1中构成理想点的个体作为xbest,引导子种群P2向理想点的位置演化,演化过程中子种群P2所获取的高质量个体通过种群重组的方式进入子种群P1,进而引导子种群P1的进化,并跳出不可行域。
3 实验与分析
为验证本文算法的性能,选择变量维度在6 到16 之间且具有凹和凸型Pareto 前沿的约束多目标优化问题CF[18]和DOC[4]测试问题集进行测试及分析。选择了基于约束支配准则的非支配排序遗传算法(Nondominated Sorting Genetic Algorithms Ⅱ based on Constrained Dominance Principle,NSGA-Ⅱ-CDP)[1]和近几年新提出的约束多目标优化算法:两阶段算法(Two-Phase algorithm,ToP[4])、推拉搜索算法(Push and Pull Search algorithm,PPS[5])和约束多目标优化的双存档进化算法(Two-Archive Evolutionary Algorithm for Constrained Multiobjective Optimization.C-TAEA)[9]作为对比。
3.1 评价指标
本实验中选取反向世代距离(Inverted Generational Distance,IGD)和超体积指标(Hypervolume,HV)作为评价指标。IGD 指标衡量的是真实Pareto 前沿中的点到所求得Pareto 前沿近似解集之间最小距离的平均值;HV 指标是指被非支配解集覆盖的目标空间区域大小。设P*是真实Pareto前沿上均匀采样的解集,PR是算法求得的Pareto前沿近似解集,其定义分别如式(13)、(14)所示:
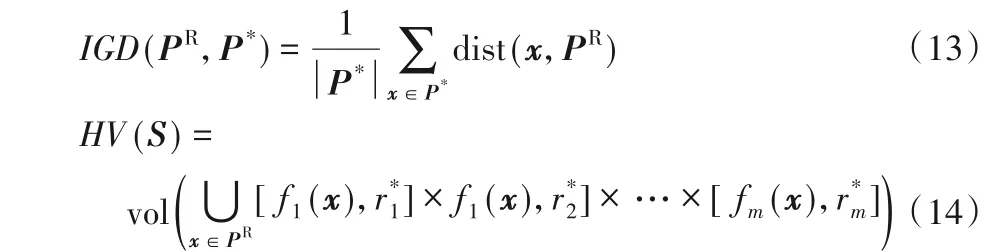
其中:dist(x,P)表示个体x∈P*到PR上离其最近个体之间的欧氏距离;|P*|是集合P*中的基数;vol(·)表示勒贝格测度;表示分布在目标空间的参考点,参考点为Pareto 前沿极值点的1.1 倍。IGD 的值越小或HV 值越大,表示该算法具有越好的收敛性和多样性,也说明PR更加近似Pareto前沿。
3.2 实验参数设置
设置种群大小N=450,根据文献[17]中的建议设置子种群N1=300,网格划分参数K=140,邻居间隔设置为5;N2=150,稳态演化的子种群划分数量m=30;所有算法的终止条件为函数评估次数达到300 000;对于所有测试问题集算法独立运行51次,最后结果取平均值。
3.3 实验结果及分析
实验比较了本文算法与NSGA-Ⅱ-CDP、ToP、PPS 和CTAEA 在测试集CF 和DOC 的IGD 和HV 指标的平均值和均方差,结果如表2和表3所示,其中粗体IGD和HV指标结果为五种算法中最优结果,NaN 表示未寻找到可行解,括号内为均方差结果。在测试集中,测试集CF1~CF3 的Pareto 前沿是这些问题在无约束情况下Pareto 前沿的一部分;测试集CF4~CF7的主要难点在于搜索前沿,因为很多Pareto 前沿的点分布在约束边界位置。相对于前者,测试集CF4~CF7 对算法是否能够有效兼顾多样性和收敛性能提出了更高的要求。测试集DOC 同时拥有目标与决策变量之间约束,更符合实际应用需求。

表2 IGD的均值与均方差对比Tab.2 Comparison of mean and mean squared deviation for IGD

表3 HV的均值与均方差对比Tab.3 Comparison of mean and mean squared deviation for HV
与NSGA-Ⅱ-CDP 和C-TAEA 算法相比,对于测试集CF 和DOC,本文算法在IGD和HV指标上均能获得较好的结果。
与PPS 算法相比,对于CF 测试集中CF3、CF4 和CF7 以及DOC 测试集,本文算法在IGD 指标和HV 指标上获得较好的结果,而PPS 算法在测试问题CF1、CF2 和CF5 上取得较好结果。
与ToP 算法相比,对于测试集中CF2、CF4 和CF7 以及DOC 测试集,本文算法在IGD 指标和HV 指标上获得较好结果,对于测试问题CF3,两种算法在HV 指标上获得了相似的结果,而ToP算法在测试问题CF1和CF5取得较好结果。
在收敛性和多样性平衡方面,协同进化过程中,单目标演化起到引导种群进化的作用,多目标演化起到维持种群多样性的作用,图3分别描绘了本文算法在DOC1问题上早中晚三个时期的两个子种群的目标空间中分布情况。从图中可以看出,在协同进化初期阶段,第一阶段的稳态演化在搜索到一定的可行解后,种群中的可行解在目标空间分布相对均匀,保持了良好的多样性;在协同进化中期阶段,子种群P2引导子种群P1演化,跳出不可行域,同时子种群P1基于网格约束分解的演化方法主要通过参考点的方式维持种群的多样性,避免收敛到局部的Pareto 前沿;在协同进化后期阶段,子种群P1引导种群演化过程结束,子种群P1中个体逐渐聚集于Pareto 前沿的一个端点,子种群P2采用的多样性管理措施发挥作用。基于邻居关系的演化方法和网格多样性管理方法在维持种群多样性方面具有良好的优势,因此,采用单目标和多目标相结合的协同进化方式在兼顾收敛性和多样性方面具有良好的收敛效果。
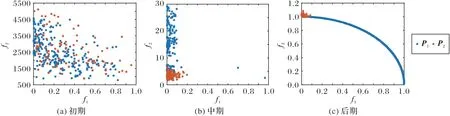
图3 DOC1的协同进化过程Fig.3 Coevolutionary process of DOC1
综上所述,本文算法在测试集上取得的良好结果,得益于多阶段和协同进化两种优化方式的良好结合,在第一阶段的稳态演化以多个子种群分别演化的形式保持种群的多样性,并搜索高质量的可行解;第二阶段的协同进化阶段以双种群协同演化的方式兼顾收敛性和多样性。其中,两个子种群分别以基于网格约束分解的方式和加权的方式实现算法的多样性和收敛性,两个子种群通过交互机制实现各自所分配任务的协同。因此,本文算法在求解具有低可行域、强约束和不连续Pareto 前沿的测试集DOC 中表现出了良好的优势,在求解更注重搜索能力的测试集CF时也具有良好的效果。
3.4 参数敏感性分析
3.4.1 子种群数量m
为研究稳态演化中设定的子种群数量对算法性能的影响,分别在测试问题CF1、CF3、DOC1、DOC4 和DOC6 上测试了当m分别为10、15、25、30、45 时的求解效果,以算法独立运行51 次结果的平均IGD 值作为评价标准,函数评价次数为300 000。测试结果如表4所示,可以看出,本文算法在稳态演化阶段中采用具有相对较低敏感性的子种群数量。
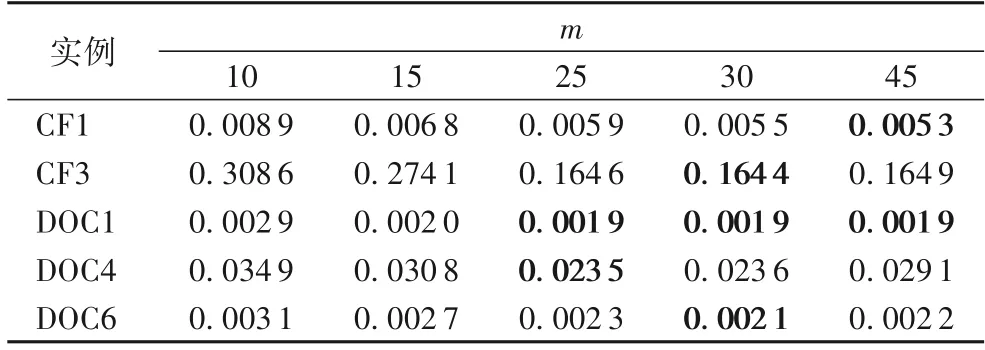
表4 m取不同值时的IGD均值对比Tab.4 Comparison of mean values of IGD with different m
3.4.2 子种群规模N2
为研究协同进化中子种群数量对算法性能的影响,本文分别在测试问题CF1、CF3、DOC1、DOC4 和DOC6 上测试了四种子种群规模(N1,N2)组合形式别为(300,50)、(300,100)、(300,150)、(300,200)时求解效果。由于本文采用基于网格约束分解的方法,所以按文献[17]中的建议设定N1=300。以算法独立运行51 次结果的平均IGD 值作为评价标准,函数评价次数为300 000。测试结果如表5所示,可以看出,本文算法在稳态演化阶段中采用具有相对较低敏感性的子种群数量。
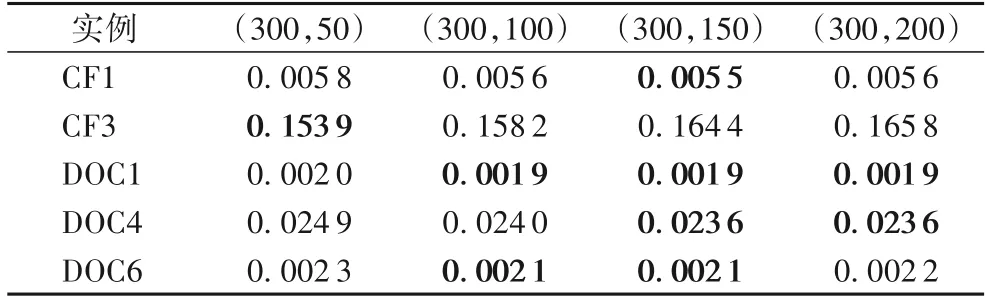
表5 N2取不同值时的IGD均值对比Tab.5 Comparison of mean values of IGD with different N2
4 实例验证
采用盘式制动设计问题[19]进一步检验本文算法的有效性。该问题具有两个目标,分别是制动器的重量和停止时间;包含四个变量,其中x1和x2分别是制动器内外圈直径,x3表示啮合力,x4表示摩擦面的数量;该问题的约束条件分别是半径之间的最小距离、制动的最大长度、压力、温度和扭矩限制,具体优化问题及约束如式(15)所示,其中:x1∈[55,80],x2∈[75,110],x3∈[1000,3 000],x4∈[2,20]。
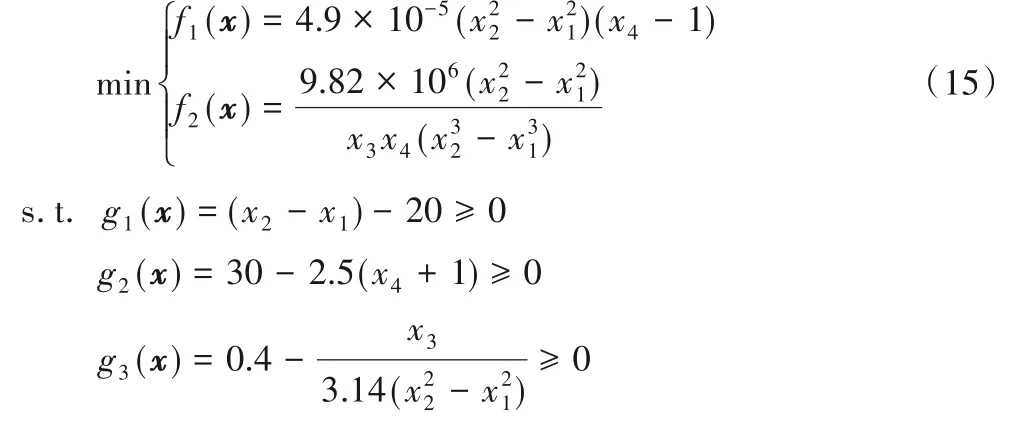
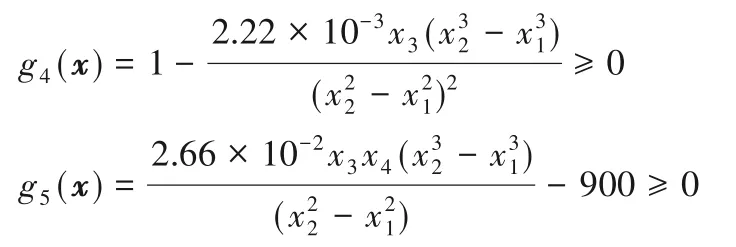
各算法在该问题上独立运行51 次,函数评价次数设定为300 000,比较求解结果HV 值的最优值(best)、均值(mean)与标准差(std),参考点按照本文算法获取的最大极值点的1.1倍设定。
求解结果如表6 所示,可以看出,本文算法较对比算法具有一定的优势。

表6 五种算法在盘式制动设计问题上的HV指标比较Tab.6 Comparison of five algorithms on disk brake design problem in terms of HV indicator
5 结语
本文提出了一个基于协同进化的约束多目标优化算法,通过网格约束分解和加权的方式实现协同进化,能有效地兼顾进化过程中算法的收敛性和多样性,并结合稳态演化方法以保证该算法前期具有良好搜索性能,最后通过测试集和实例验证了算法的有效性。算法的不足之处在于采用基于网格约束分解的方法导致算法种群规模较大,相同评价次数的情况下,本文算法迭代次数偏低,影响求解质量,因此,多样性管理措施将是未来主要研究方向。
