贪婪的量测划分机制下的多传感器多机动目标跟踪算法
2021-07-29朱圣棋房云飞
杨 标 朱圣棋 余 昆 房云飞
(西安电子科技大学雷达信号处理国家重点实验室 西安 710077)
1 引言
随机有限集[1](Random Finite Set, RFS)自提出以来,因其优越的跟踪性能以及较低的算法复杂度而备受关注[2]。多目标多伯努利(Multi-target Multi-Bernoulli, MeMBer)滤波器[1]是基于RFS理论的一种有效的多目标跟踪滤波器,其能够有效地对多目标的个数和状态进行有效地估计。但是传统的MeMBer滤波器只能对(线性和非线性系统下)具有单一运动模式的目标进行跟踪,一旦目标具备较强的机动特性,传统的MeMBer滤波器便会难以为继。因此,在MeMBer滤波器的基础上,国内外学者进行了大量的研究[3–5]和改进。
在机动目标跟踪领域,交互式多模型[6,7](Interacting Multiple Mode, IMM)策略是一种高效的机动目标状态预测方法。其首先利用当前的量测信息对模型概率进行预测更新;再利用更新后的模型概率和得自不同模型的目标状态预测值,对机动目标的状态进行加权混合估计;最终达到对机动目标状态正确预测的目的。IMM策略常常作为一种有效的机动目标状态预测方法嵌入多目标跟踪算法[8,9]中,以达到对多个机动目标的个数、状态进行有效的估计,并输出各个目标航迹的目的。
对于低检测概率目标的跟踪问题,最为直接有效的方法为多个传感器共同检测,所以多传感器多目标跟踪算法在微弱目标跟踪领域扮演着重要的角色。文献[10,11]介绍了广义的多传感器(Multi-Sensor, MS)概率假设密度(Probability Hypothesis Density, PHD)滤波器,但是因其具有较大的算法复杂度而难以实现。所以在文献[12,13]提出了一种复杂度较低的迭代校正(Iterative Correction, IC)策略下的多传感器PHD和多传感势平衡概率假设密度(Cardinality balance Probability Hypothesis Density, CPHD)滤波器,但算法复杂度仍旧较高。最近,文献[14,15]通过提出贪婪的量测划分策略,提出了一种计算上近似实现的多传感器CPHD滤波器和多传感器MeMBer滤波器,极大地提高了多传感器多目标跟踪算法的运算效率。
现代军事中,往往对低检测概率(如隐形飞机,雷达散射截面RCS小的目标等)下高机动目标跟踪算法的要求极高,因此针对低检测概率下高机动目标跟踪算法的研究具有重要的意义。本文利用IMM策略、MeMBer滤波器以及基于贪婪的量测划分策略的多传感器技术提出了一种新的交互式多传感器多目标多伯努利(Interacting Multiple Mode Multi-Sensor Multi-target Multi-Bernoulli filter,IMM-MS-MeMBer)滤波器,并与传统的基于迭代校正方法下的交互式迭代校正多传感器多目标多伯努利(Interacting Multiple Mode Iterative Correction Multi-sensor Multi-target Multi-Bernoulli filter, IMM-IC-MeMBer)滤波器、基于单模型下的多传感器多目标多伯努利滤波器(Multi-Sensor Multitarget Multi-Bernoulli filter base on Constant Velocity model, CV-MS-MeMBer)、交互式单传感器多目标多伯努利(Interacting Multiple Mode Single Sensor Multi-target Multi-Bernoulli Filter, IMMSS-MeMBer)滤波器进行对比。验证了杂波环境中,所提IMM-MS-MeMBer滤波器对多个低检测概率高机动目标的优良跟踪性能以及其在运算效率上的优势。
2 系统模型
2.1 动态模型


2.2 多传感器量测模型

3 贪婪的多传感器量测划分
贪婪的多传感器量测划分算法主要分为以下5步:


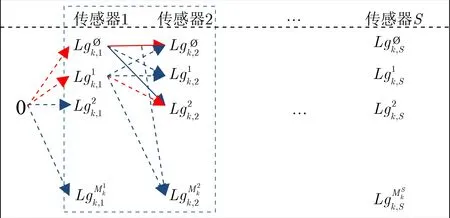
图1 贪婪的多传感器量测选择

4 交互式多传感器多伯努利粒子滤波算法
本节在IMM算法、贪婪的多传感器量测划分、传统的MeMBer滤波器的基础上,推导了一种新的IMM-MS-MeMBer滤波器。
4.1 IMM-MS-MeMBer预测


4.2 IMM-MS-MeMBer更新

k时刻目标的个数估计为
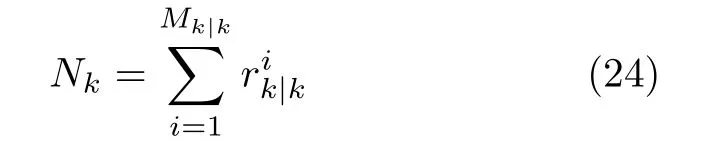
5 数值实验
5.1 实验环境


图2 真实目标轨迹
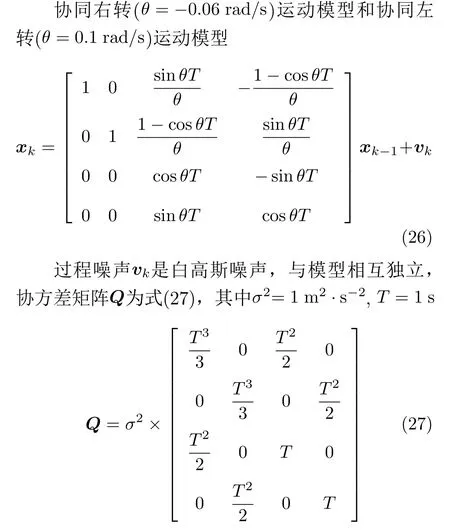
在模型概率预测中,模型间转移考虑为随机的,认为各个模型间相互转移的概率相同,所以实验中模型转移概率矩阵设置为
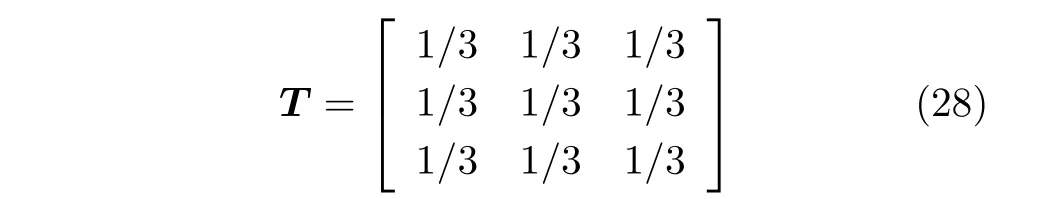
实验中共设置S=5个传感器,位置分别为[0,0], [-400,-400], [400,400], [-400,0]和[400,0],量纲为m。传感器量测模型[15]为

5.2 实验结果分析
图3和图4分别为传感器检测概率PD=0.5, 杂波率λ=8时,IMM-MS-MeMBer滤波器对多机动目标的位置和速度估计效果图。由图3和图4可以看出本文所提IMM-MS-MeMBer滤波器能够在杂波环境中,实现对多机动目标位置和速度的估计。
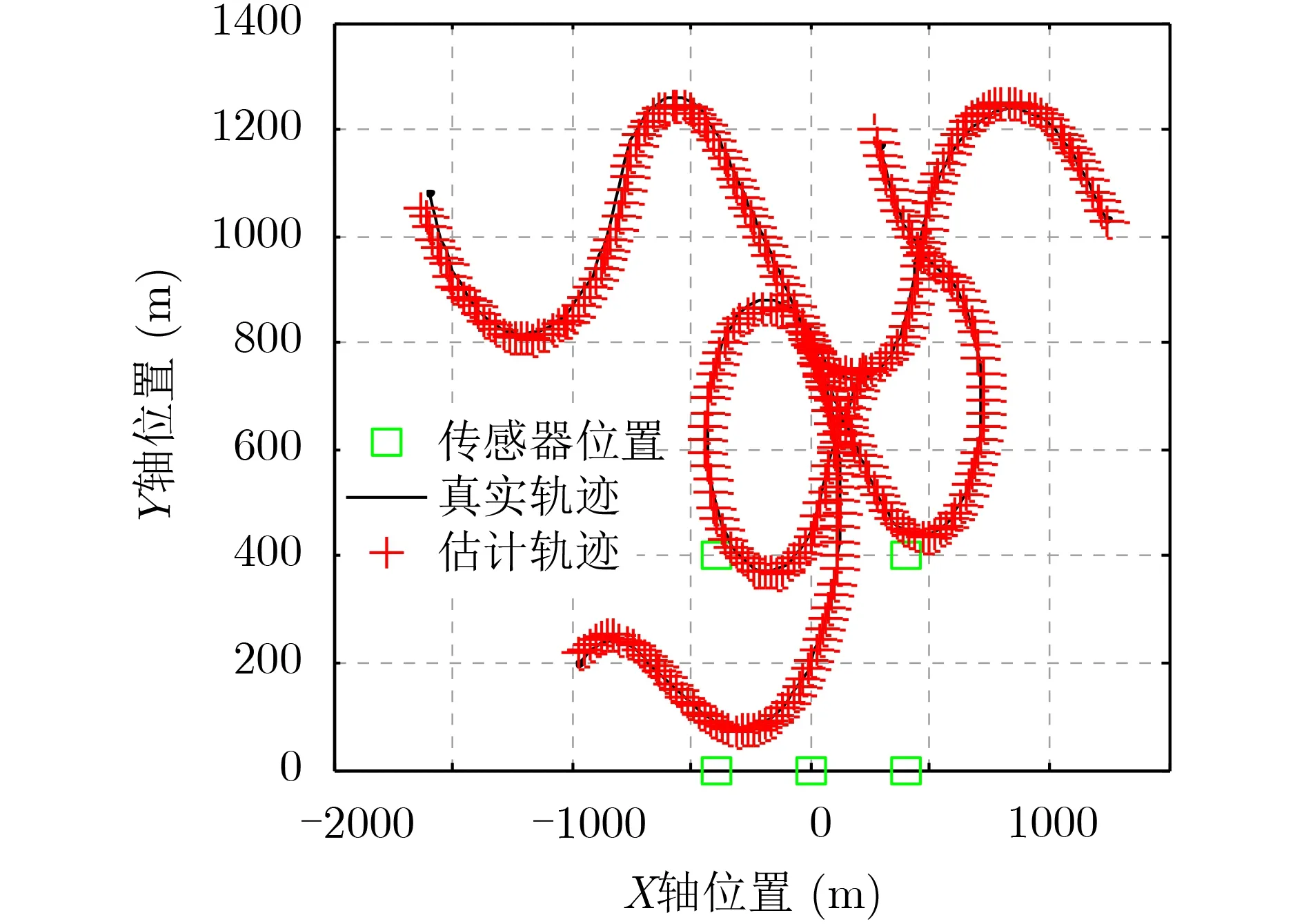
图3 多机动目标位置估计
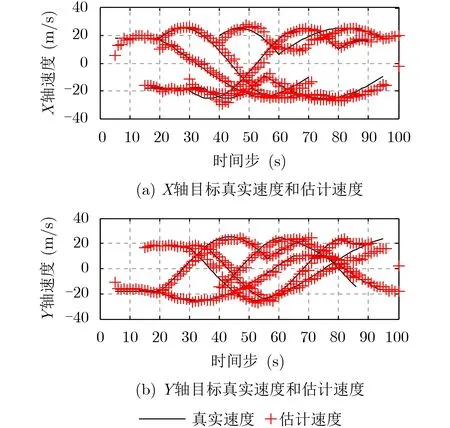
图4 多机动目标速度估计
表1给出了图5、图6和图7中图例的说明。图5的图例中,0代表真实机动目标的个数。图5和图6分别为不同算法、不同条件下多机动目标个数的估计、OSPA误差估计图。通过观察图5和图6,可得:(1)本文所提IMM-MS-MeMBer滤波器在不同杂波率下都能够有效地实现对多机动目标个数的估计,当目标新生和死亡时,不同杂波率下IMMMS-MeMBer滤波器都会出现OSPA距离误差峰值。同等条件下,IMM-MS-MeMBer滤波器比IMM-MS-CPHD滤波器对目标状态和个数的估计性能好,估计得到的OSPA距离误差更小,这是因为IMM-MS-MeMBer滤波器对目标状态提取时不需要对粒子进行聚类,而IMM-MS-CPHD滤波器则需要通过聚类算法来提取目标状态,滤波器性能的好坏受到了聚类算法的影响;(2)在同等条件下,随着时间推移,单模型下CV-MS-MeMBer滤波会因为机动目标状态估计中的模型失配问题,逐渐丢失目标,所以不能得到正确的目标个数估计,OSPA距离误差也会随着时间的推移越来越大。相较于单模型下CV-MS-MeMBer滤波,IMM-MSMeMBer滤波则能够有效解决单模型下因模型失配造成的目标丢失问题;(3)当检测概率较低(如PD=0.5和PD=0.7)时,IMM-SS-MeMBer滤波器根本无法对多个机动目标的状态形成有效的估计,随着时间的推移,目标个数估计性能会急剧恶化,OSPA距离误差也会急剧增大。但是随着检测概率提升,IMM-SS-MeMBer滤波器对目标个数的估计性能会逐渐逼近正确值。相较于IMM-SS-MeMBer滤波器,在PD=0.5时,本文所提IMM-MSMeMBer滤波器则能够准确地估计多机动目标的个数,且具有较小的OSPA距离误差。说明了本文所提IMM-MS-MeMBer滤波器能够解决目标低检测概率难以跟踪的问题;(4)相同条件下,与传统的多传感器IMM-IC-MeMBer滤波器相比,IMM-MSMeMBer滤波器在对多机动目标个数的估计上也能达到理想的效果且相对稍加稳定,在OSPA距离误差上,IMM-MS-MeMBer滤波器明显更小,说明相同条件下IMM-MS-MeMBer滤波器具备更加优越的性能。

表1 图5、图6和图7中图例的含义说明
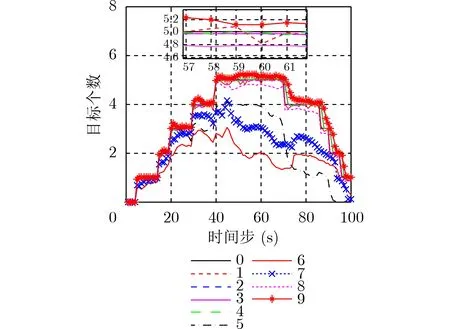
图5 多机动目标个数的估计
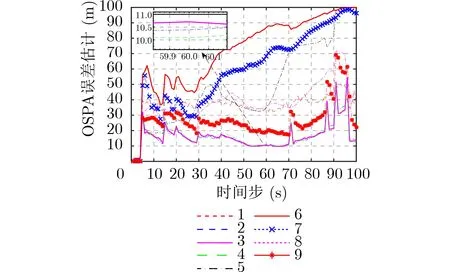
图6 多机动目标OSPA误差距离估计
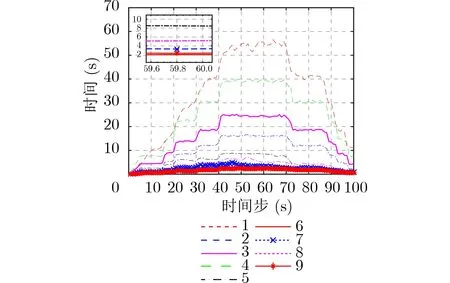
图7 不同条件不同算法运算复杂度统计
通过图7对不同条件下不同算法运行时间的统计,可以看出相较于传统的IMM-IC-MeMBer滤波器,本文所提的IMM-MC-MeMBer滤波器在计算复杂度上得到了极大的改善;由于引入了IMM算法对机动目标的状态进行预测,所以相较于单模型下的CV-MS-MeMBer滤波器,本文所提的IMMMC-MeMBer滤波器需要更大的运算量,但是相较于性能方面的提升,计算复杂度的提升是可以接受的;此外,结合IMM算法和贪婪的量测划分算法可以得到IMM-MS-CPHD滤波器。IMM-MSCPHD滤波器相较于IMM-MC-MeMBer滤波器具有较低的运算复杂度,这是因为本质上IMM-MSCPHD滤波器与IMM-MC-MeMBer滤波器的机理是完全不同的,IMM-MS-CPHD滤波器会对每个时刻的粒子总数进行约束,它能够随着时间的迭代保持一个稳定的复杂度。但是IMM-MC-MeMBer滤波器中的伯努利成分则会随着时间的迭代呈指数性增长,即使预先设定了伯努利成分个数的上限,算法的运算花费也会随着时间的迭代而达到一个峰值才能保持稳定。
6 结论
本文提出一种新的IMM-MS-MeMBer滤波器,并通过数值实验得到了以下结论:第一,IMMMS-MeMBer滤波器通过引入当前量测信息对目标的运动状态进行多模加权估计,从而解决了机动目标的状态预测问题;第二,IMM-MS-MeMBer滤波器通过贪婪的量测划分策略实现了量测的有效划分,进而有效地解决了目标的低检测概率能以检测和跟踪问题;第三,IMM-MS-MeMBer滤波器能够在杂波环境中利用角度和多普勒信息实现对目标的位置和速度的联合估计;第四,IMM-MS-MeMBer滤波器相对于IMM-IC-MeMBer滤波器,极大地提高了多传感器多机动目标算法的运算效率。
