相参处理间隔较短条件下基于稀疏重构及形态成分分析的航管雷达风电场杂波抑制
2021-07-29何炜琨毕峰华王晓亮
何炜琨 毕峰华 王晓亮 张 莹
(中国民航大学天津市智能信号与图像处理重点实验室 天津 300300)
1 引言
风能是一种清洁而稳定的新能源,在环境污染和温室气体排放日益严重的今天,风力发电作为全球公认的可以有效减缓气候变化、提高能源安全、促进低碳经济增长的方案,得到各国政府、机构和企业的高度关注[1,2]。近年来我国风力发电产业飞速发展[3]。研究表明,风电场回波可能对航管监视雷达的目标检测产生负面影响[4–9],使得航管监视雷达出现目标检测概率降低、虚警率上升等问题。因此,风电场杂波抑制技术的研究对于提升航管监视雷达工作性能、保障空中交通安全具有重大意义。
近些年来,国内外很多学者从信号处理方面对风电场杂波抑制技术展开研究。Naqvi等人[10]及南京电子技术研究所曹永贵等人[11]分别利用匹配追踪(Matching Pursuit, MP)和正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法对杂波进行抑制,两种算法都需要构造风轮机杂波字典,计算量较大且需要一定量的先验信息才能保证算法性能。Karabayir等人[12]提出一种基于CLEAN算法的风轮机杂波抑制方法,通过构造仅含风轮机杂波的辅助回波信号,将该回波信号从雷达接收回波中减去实现风轮机杂波抑制,但是在构造辅助回波信号的时候需要一定量先验信息。本文在航管雷达风电场杂波抑制方面也开展了一系列研究工作。对于风电场杂波(或杂波扩展主瓣)与飞机目标不在同一距离单元的场景,利用风轮机杂波的频谱展宽特征使用谱中心补偿方法抑制杂波[13],对于风电场杂波(或杂波扩展主瓣)与飞机目标在同一距离单元的场景,在回波数据充足并且具有一定先验信息的基础上基于缺省数据幅度和相位估计(Gapped-data Amplitude and Phase EStimation, GAPES)算法实现风轮机回波两个相反多普勒频率峰值之间缺省数据的重构,对重构后的数据利用杂波的周期性进行抑制[14]。
Uysal等人[15]根据稀疏优化理论,提出基于形态成分分析(Morphological Component Analysis,MCA)算法实现风轮机杂波抑制,根据风轮机杂波与飞机目标在不同变换域的稀疏性,分离出风轮机杂波。该方法可以处理目标与杂波处于同一距离单元问题,同时由于不需要建立字典,计算效率相比MP等贪婪算法更高。之后第38研究所的夏鹏等人[16]利用该方法对凝视模式下的风轮机杂波进行了有效抑制。但是在扫描模式中,相参处理间隔(Coherent Processing Interval, CPI)较短常常会造成相干脉冲数较少,由此导致回波信号谱分辨率降低及风轮机杂波的时变多普勒特征不明显等问题,MCA算法性能受到影响,因此本文针对短CPI条件下风电场先验信息不足且杂波(或杂波扩展主瓣)与目标处于同一距离单元场景下的风轮机杂波抑制问题进行讨论。
本文针对实际雷达系统中短CPI造成的谱分辨率较低及各信号分量变换域稀疏性不明显导致MCA算法性能下降的问题,首先利用稀疏重构算法提高信号谱分辨率和稀疏性,在此基础上利用MCA算法完成对风轮机杂波的抑制。
2 基于MCA的风电场杂波抑制
MCA算法利用不同信号在不同变换域的不同稀疏特性实现信号的分离[15]。风轮机由于叶片不断运动旋转会产生时变多普勒的特征,因此认为风轮机杂波在时频域相比频域更加稀疏;在一个CPI内,飞机目标可认为是恒速运动的,所以其多普勒频率是恒定的,因此认为飞机目标的频域稀疏性更好[15,16]。
风电场杂波抑制问题实际上就是将回波信号中飞机目标和风轮机杂波进行分离问题。已知飞机信号和风轮机杂波可以分别在频域和时频域进行稀疏表示,根据MCA的理论,可转变为求解信号与杂波在频域和时频域的最优表示系数的问题。针对此问题可通过分裂增广拉格朗日收缩算法(Split Augmented Lagrangian Shrinkage Algorithm,SALSA)[17]迭代优化求解,完成信号的分离。MCA算法中变换域矩阵A通常满足帕塞瓦尔形式[17],即
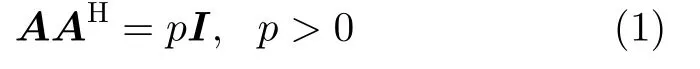
其中,(·)H表示共轭转置;p为帕塞瓦尔常数,通常设置为1;I是单位阵。
依据MCA算法原理,算法性能取决于待分离信号(目标与杂波)是否能在不同的变换域进行稀疏表示。实际应用中存在的短CPI条件下接收到的雷达回波信号由于观测时间较短,飞机信号和风轮机杂波的频域稀疏性相近且风轮机杂波的时变多普勒特征不够明显,此时MCA算法的性能将会受到影响。
3 稀疏重构算法
3.1 雷达回波稀疏重构
根据以上分析可知,风轮机杂波会产生时变多普勒,因此在时频域中稀疏性比频域要好。但在瞬态时间内,风轮机多普勒频率几乎不变,认为瞬态风轮机回波可在频域稀疏表示,同时飞机目标可在频域稀疏表示,因此风电场雷达回波滑窗得到的瞬态信号分量(包括飞机、风轮机)可以在频域进行稀疏表示。
本文所采用的稀疏重构算法,首先短CPI回波数据相当于较长CPI回波数据发生了尾部数据缺省;其次依据风电场雷达瞬态回波可以在频域稀疏表示理论,给出缺省数据的重构算法,即对滑窗得到的逐个信号分量基于分裂增广拉格朗日收缩算法(SALSA)求解回波数据在频域的最优表示系数,完成各信号分量中缺省数据的恢复,再由恢复后的多个信号分量逆滑窗重构完整数据,提升短CPI情况下雷达回波谱分辨率及信号的稀疏特征。
3.1.1 问题描述

其次利用增广拉格朗日方法(Augmented Lagrangian Method, ALM)[19]反复迭代,求解w1和x1,直到收敛。具体实现如表1所述。
表1中,d类似于拉格朗日乘数,通常初始化为0向量;µ为步长。式(8)中的优化问题可以利用软阈值方法求解;式(9)中优化问题是一个有约束的最小二乘问题,可利用洛必达法则及矩阵运算对其进行求解。上述求解过程可进一步进行简化,如表2所示。


表1 ALM迭代求解算法

表2 对应化简求解算法
式(12)避免求逆运算,以此降低该算法的计算量,因此得到最终算法,如表3所示。以此获取第1个信号分量中缺省数据的恢复。短CPI数据稀疏重构的过程就是逐个信号分量中缺省数据恢复的过程。

表3 最终求解算法
3.2 基于稀疏重构及MCA的风电场杂波抑制
依据3.1节,航管雷达短CPI回波数据的稀疏重构问题,可转变为滑窗后逐个信号分量通过SALSA在频域迭代优化求解最优表示系数,继而进行逆滑窗完成缺省数据的恢复问题,在此基础上基于传统MCA算法进行杂波抑制,以此解决短CPI条件下MCA杂波抑制性能下降的问题。基于稀疏重构及MCA的风电场杂波抑制实现框图如图1所示。
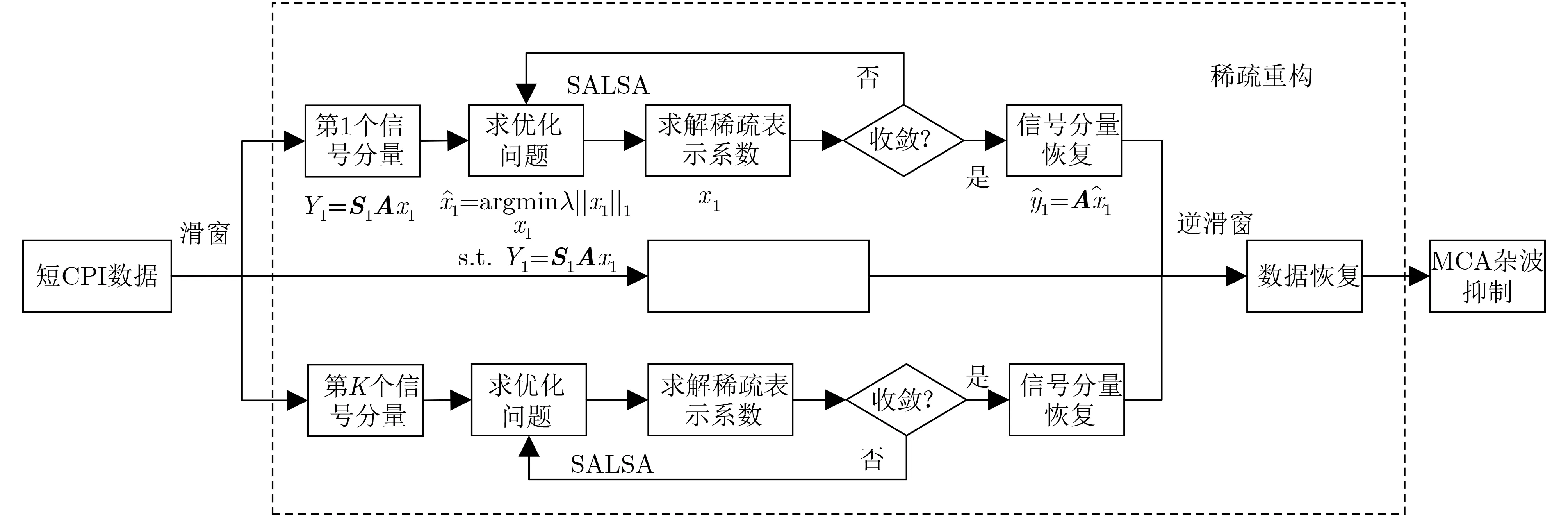
图1 基于稀疏重构及MCA算法的风电场杂波抑制实现框图
4 实验结果及分析
4.1 实验设计
本文实验主要从雷达视线与风轮机某个叶片是否发生垂直两种情况进行分析。对于一个CPI内风轮机某个叶片与雷达视线是否垂直,可以利用风轮机杂波在垂直条件下会产生频谱展宽进行判断;还可以利用本课题组之前方案,基于霍夫变换进行判断[14],在此不再赘述。
首先雷达视线与风轮机单个叶片发生垂直条件下,基于MCA算法对仿真数据进行处理,并利用实测数据进行验证,对实测的仅含风电场杂波数据进行地杂波滤除后计算风轮机杂波平均功率,再按照一定的信杂比(Signal-to-Clutter Ratio, SCR)约束人为添加飞机目标,对比分析实验结果。其次雷达视线与单个风轮机叶片非垂直情况下,针对仿真及实测数据分别基于MCA和稀疏重构后的MCA算法进行风电场杂波抑制,对比分析实验结果及算法性能。
4.2 垂直条件下的风电场杂波抑制
本节主要讨论短CPI条件下雷达视线与某一叶片发生垂直情况下的杂波抑制问题。分别针对仿真及实测数据进行处理验证。
4.2.1 仿真数据
参考典型风轮机模型以及雷达的相关参数[14],仿真参数如表4、表5所示。提取某一特定距离单元(距离单元数为221)的接收信号,接收信号对应的幅度谱如图2(a)所示,圆圈处为飞机目标。基于MP算法杂波抑制后的结果如图2(b)所示;基于MCA算法分离飞机目标及风轮机杂波,结果如图2(c)和图2(d)所示。可以看出,无论MP算法还是MCA算法都能有效地完成杂波抑制。
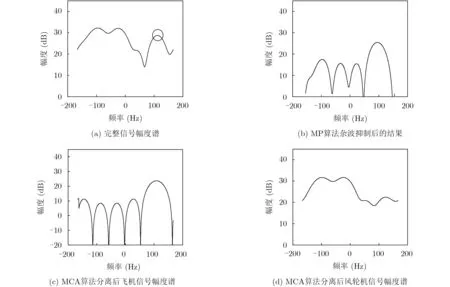
图2 MP及MCA算法的杂波分离(抑制)结果
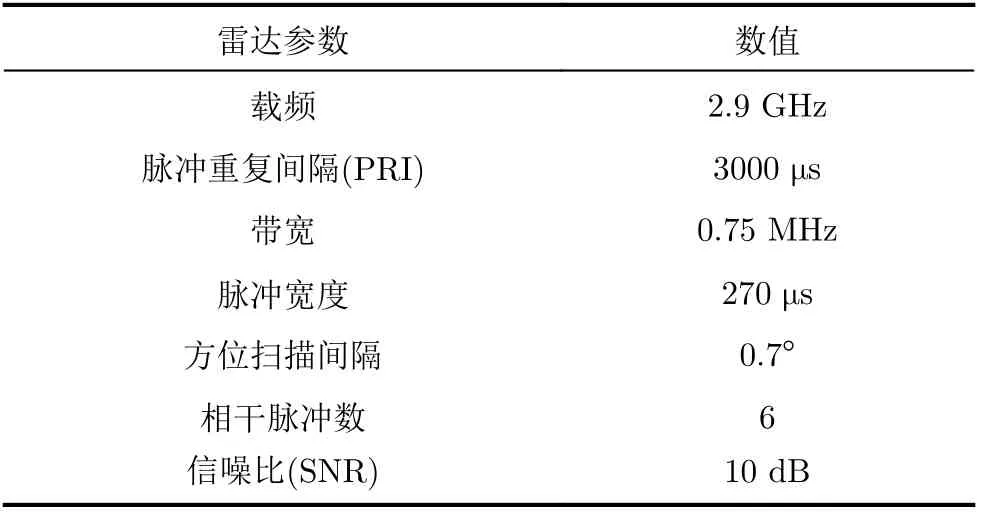
表4 雷达参数

表5 风轮机参数
4.2.2 实测数据
实测数据的相关参数如表6所示。从只有风电场杂波的实测数据中筛选垂直状态下相应距离单元回波数据(第698帧364距离单元数据)。去0通道后以SCR-20 dB为约束加入飞机目标后的信号幅度谱如图3(a)所示,圆圈处为飞机目标。此时可以观察到幅度谱右侧存在明显展宽。对该数据基于MP算法及MCA算法进行杂波抑制,从图3中可以看出,MP算法杂波抑制后的结果如图3(b)所示。基于MCA算法杂波抑制结果如图3(c)和图3(d)所示。由图3可看出,MP算法杂波抑制效果不是很理想;MCA算法处理后飞机信号可以分离出来,大部分风轮机杂波得到有效抑制。
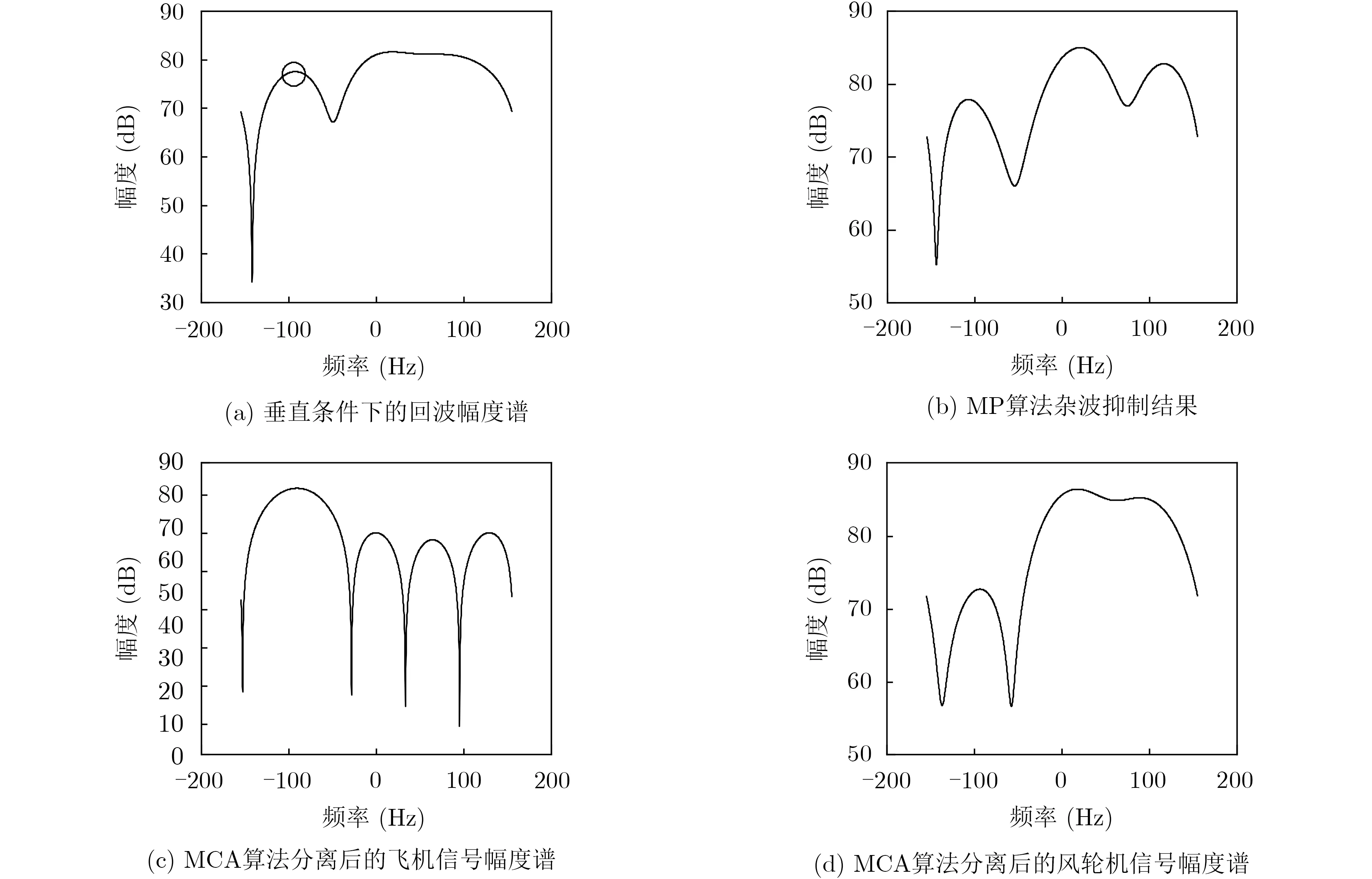
图3 MP及MCA算法的杂波分离(抑制)结果
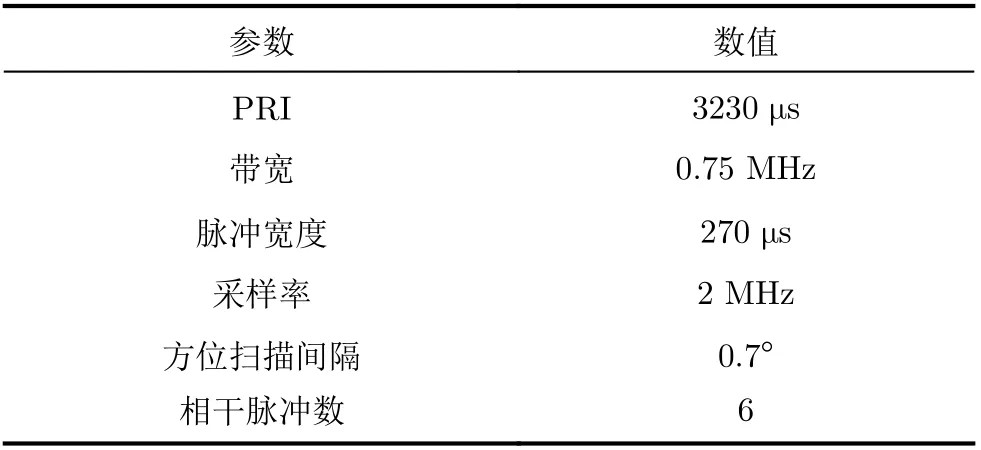
表6 实测数据相关参数
由实验结果可知,短CPI条件下,当雷达视线与风轮机单个叶片发生垂直时,MCA算法更容易在频域获取飞机信号的最优表示系数,以此解决该条件下的风轮机杂波抑制问题。但是MP算法的性能依赖于字典,并不稳定。进而相对于MCA方法而言,MP算法的杂波抑制性能难以保证。
需要说明的是,当飞机信号频谱在风轮机频谱展宽范围内时,MCA算法也能有效抑制风轮机杂波。因此MCA算法可以解决短CPI条件下雷达视线与单个叶片发生垂直时的杂波抑制问题。
4.3 非垂直条件下的风电场杂波抑制
本节主要讨论短CPI条件下信号谱分辨率较低、稀疏特征不明显导致MCA算法性能下降的问题。分别针对仿真及实测数据进行处理并验证。
4.3.1 仿真数据
仿真参数如表4、表5所示,其中相干脉冲数为4,单个叶片与雷达波束初始夹角为60°。雷达回波幅度谱如图4(a)所示,圆圈处为飞机目标。对该数据基于传统MCA算法及本文方法进行杂波抑制,结果如图4所示。
从图4中可以看出短CPI条件雷达视线与某个叶片非垂直状态下,回波信号谱分辨率较低,飞机和风轮机回波的频域稀疏性相近且风轮机回波的时频域稀疏性不明显,导致MCA算法不能进行有效的杂波抑制;稀疏重构后数据回波谱分辨率有所提高,飞机信号的频域稀疏性相对更好,此时利用MCA算法可以得到想要的飞机信号。因此稀疏重构后的MCA算法可以解决短CPI条件下雷达视线与单个叶片非垂直时的杂波抑制问题。多次实验发现当相干脉冲数小于等于4个时,MCA算法难以完成杂波抑制,此时可以采用本文的稀疏重构与MCA结合的算法进行处理。
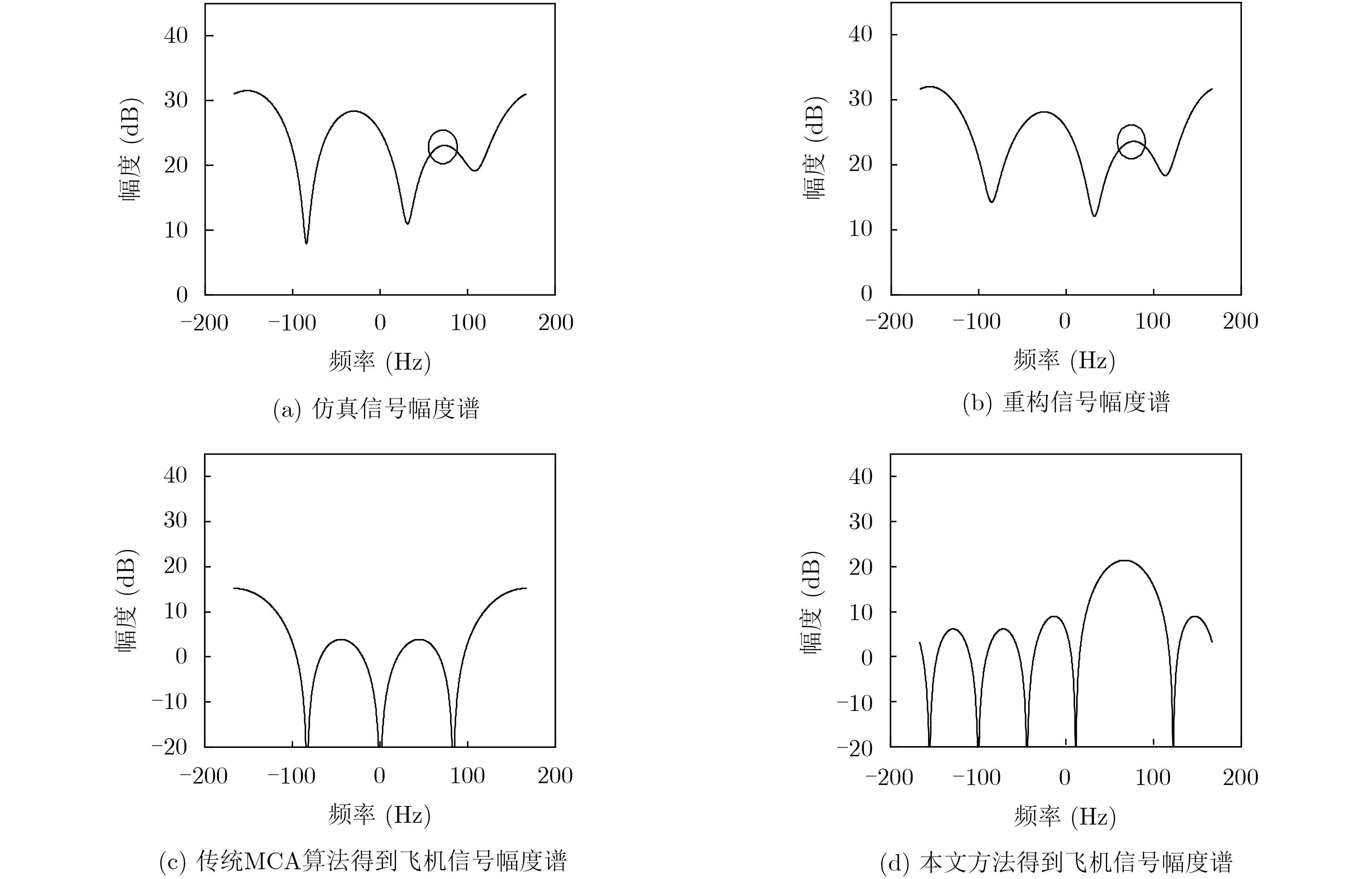
图4 传统MCA算法和本文方法仿真结果
4.3.2 实测数据
实测数据的相关参数如表6所示。为得到短CPI实测数据,文中实测数据在已知杂波所在距离单元时,提取该距离单元(第30帧416距离)风电场杂波实测数据,在此基础上,根据该距离单元杂波的平均功率及相应的SCR,相干叠加仿真飞机目标回波(雷达参数与实测数据所用雷达参数一致),以此构造待处理的雷达回波数据。选取前5个脉冲数据去零通道后在SCR约束下添加飞机目标后的幅度谱如图5(a)所示,圆圈处为飞机目标。对该数据基于传统MCA算法及本文方法进行杂波抑制,结果如图5所示。
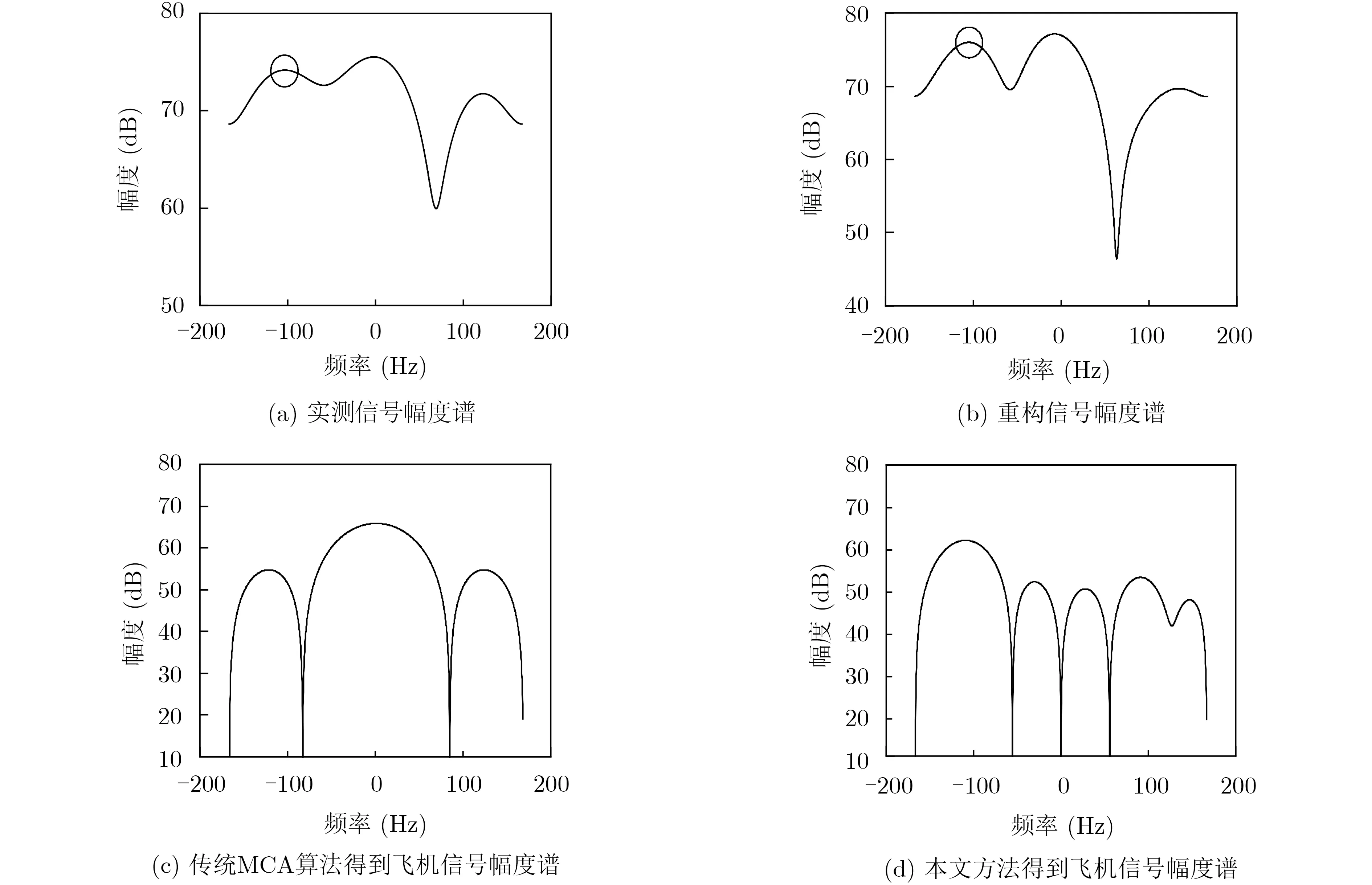
图5 传统MCA算法和本文方法实测结果
通过对实测数据的处理,可以得出与仿真数据同样的结论,稀疏重构可以提高回波信号谱分辨率及稀疏特性,进而提升MCA算法的杂波抑制性能。
需要说明的是,当回波频谱里无法体现飞机信号特性时,该稀疏重构算法应用受限。另外在多次实验中尝试较长CPI接收的数据中低于40%的数据遭遇空间强干扰导致其中某些数据无效时,该稀疏重构算法能将完整信号恢复出来,再利用MCA算法可以对风轮机杂波成功抑制。
5 结束语
针对短CPI导致的航管监视雷达回波数据谱分辨率降低及信号分量变换域稀疏特性不明显,难以采用传统MCA算法对杂波进行抑制的问题,本文提出稀疏重构算法和MCA算法结合来解决。首先稀疏重构处理能提高短CPI条件下回波数据谱分辨率和稀疏特性,其次MCA算法可以处理目标与杂波处于同一距离单元问题。实验结果表明,针对短CPI造成的有效数据不足问题,经过稀疏重构后信号的谱分辨率明显提高,同时飞机信号的频域稀疏性有所提升,此时MCA算法能够将飞机信号分离出来,同时杂波得到有效抑制。与MP算法相比,本文方法的性能不受限于字典的构建。另外,需要说明的是,本文方法适应于一个距离单元存在一台风轮机的情况,对于一个距离单元存在多台风轮机的情况,是后续的研究重点。
