基于IGWO-BP算法的轨道交通短时客流预测*

张艺铭 陈明明 石 磊 康蓉桂

（兰州交通大学交通运输学院 兰州730070）

0 引 言

客流计划是对运输计划期间线路客流的规划。传统意义上的客流预测选取中长期的时间跨度，目的是为线网规划及行车计划编制提供依据[1]。随着乘客对公共交通服务水平要求的提高，根据短时客流对运营情况进行及时的反馈与调整，已成为运营工作的重要环节。轨道交通短时客流预测是指在线网线路的稳定运营阶段，对未来某一时间段内线路、区间、车站的客流进行短期预测，其预测结果的时间跨度一般在5～15 min[2]。精确的预测结果对轨道交通运营有着重要意义。若预测客流量远高于实际客流量，会造成列车满载率过低，增加运营成本；若预测客流量远低于实际客流量，则导致列车拥挤度过高，服务质量下降。

与中长期客流相比，短时客流具有更强的随机性和非线性，传统的预测方法已经不适用于短时客流预测。短时客流预测常用的方法有：卡尔曼滤波、灰色理论、支持向量机、深度学习。J.Roos等[3]考虑历史数据的不完整性，提出1种基于动态贝叶斯网络的方法，通过结构期望最大化（EM）算法学习模型的结构和参数，然后引导滤波器进行预测；白伟华等[4]通过异常值识别扩展了卡尔曼滤波，使其能对噪声进行识别和过滤来进行短时交通流预测。帅斌等[5]考虑铁路客流在特殊时段内具有波动性和随机性，分布并不均衡，采用灰色GM模型进行客流量预测；王兴川等[6]构建基于小波分解与重构的GM-ARIMA模型来预测短时客流。郭旷等[7]基于周期性差分自动平滑回归模型和支持向量机理论，构建了短时客流预测组合模型，捕捉短时客流的周期性特征和局部非线性特征，并引入广义自回归条件异方差模型来构建短时客流不确定性预测模型；Sun等[8]设计了小波-支持向量机混合模型，运用小波技术对客流数据进行高低频分解，然后运用SVM进行预测。赵阳阳等[9]为降低样本噪声对客流预测模型的干扰,结合深度学习理论,提出了1种基于经验模态分解与长短时记忆神经网络的短时地铁客流预测模型；Hao等[10]提出了1种基于注意力序列模型的端到端深度学习框架，用于预测大规模地铁系统中的短期客流；赵建立等[11]提出1种将卷积神经网络（CNN）与残差网络（resNet）相组合的预测模型，用于城市轨道交通多站点短时客流量预测问题。卡尔曼滤波和灰色理论是基于参数的预测模型，通过捕获能够代表数据特征的参数，在有限的维度上建立预测模型。参数模型的本质是对均值的预测，无法预测极值，在预测非线性和不确定性客流量时，其预测性能变差。支持向量机、深度学习是非参数的预测模型，它对目标函数不做过多的假设，能够在没有先验知识的情况下，通过对训练数据进行拟合而学习出某种映射关系，鲁棒性较强，能够解决极值问题，在处理非线性和随机性较强的短时客流预测问题上具有较大优势。

BP神经网络是深度学习的1种类型，具有良好的自学习和自适应能力，已被大量应用于流量预测[12-14]。但是，传统的BP网络对初始权值阈值敏感，在训练过程中极易陷入局部最优而找不到具体问题的解。灰狼优化算法（GWO）是由澳大利亚学者S.Mirjalili等[15]提出的1种元启发式算法，它是受到了灰狼捕食猎物活动的启发而开发的1种优化搜索算法，具有结构简单、概念清晰、容易实现、全局性能好的特点[16]，在路径优化、故障诊断、性能检测、参数优化方面已获得了良好效果，但在客流量预测方面的应用较少。

本文研究了基于灰狼优化算法和BP神经网络的短时客流预测方法。计算不同时间段历史客流数据的相关系数，确定BP神经网络的输入输出方式；用余弦收敛因子和动态权重替代原始灰狼优化算法中的线性收敛因子和固定权重；用改进后的灰狼优化算法优化BP神经网络的权值和阈值。

1 轨道交通短时客流预测分析

在预测下1个时间段客流量时，一般要进行客流量调查，取得相关资料，结合过去的客流量统计和客流量变化规律，在本时间段客流计划实际完成情况的基础上加以确定。用{Xi，j|1≤i≤I，1≤j≤J}表示第i天第j个时间段的历史客流量（单位：人次）。其中：I为总天数；J为时间段总数；用{X I+1，j|1≤j≤J}表示预测客流量（单位：人次）；则轨道交通的短时客流量预测见图1。

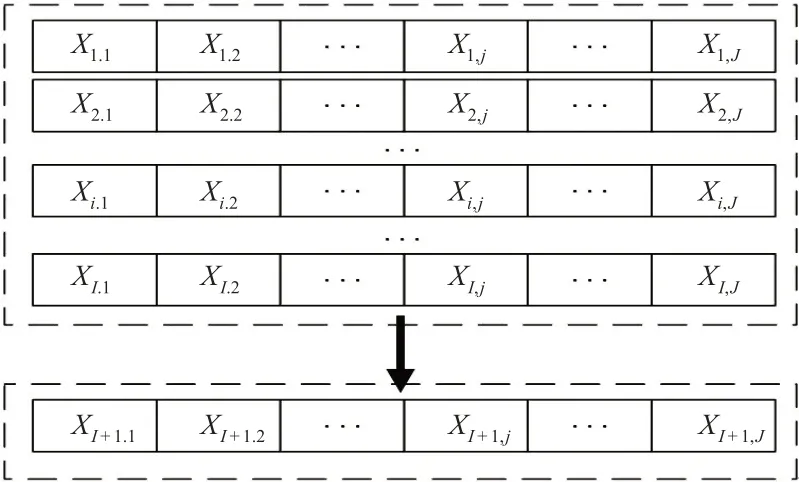
图1 轨道交通的短时客流量预测Fig.1 Forecasting the short-term passenger flow for rail transit

2 IGWO-BP算法

轨道交通短时客流预测是依靠站点的历史客流数据进行的。本文获取站点历史进站客流数据并对原始数据进行处理；按照BP网络的节点数选取规则构建神经网络并初始化权值和阈值；用改进的灰狼优化算法（IGWO）对初始化的权值和阈值寻优，将适应度最好的权值和阈值输出作为BP网络的最优权值和阈值；输入客流数据训练BP网络并输出预测结果。算法流程见图2。

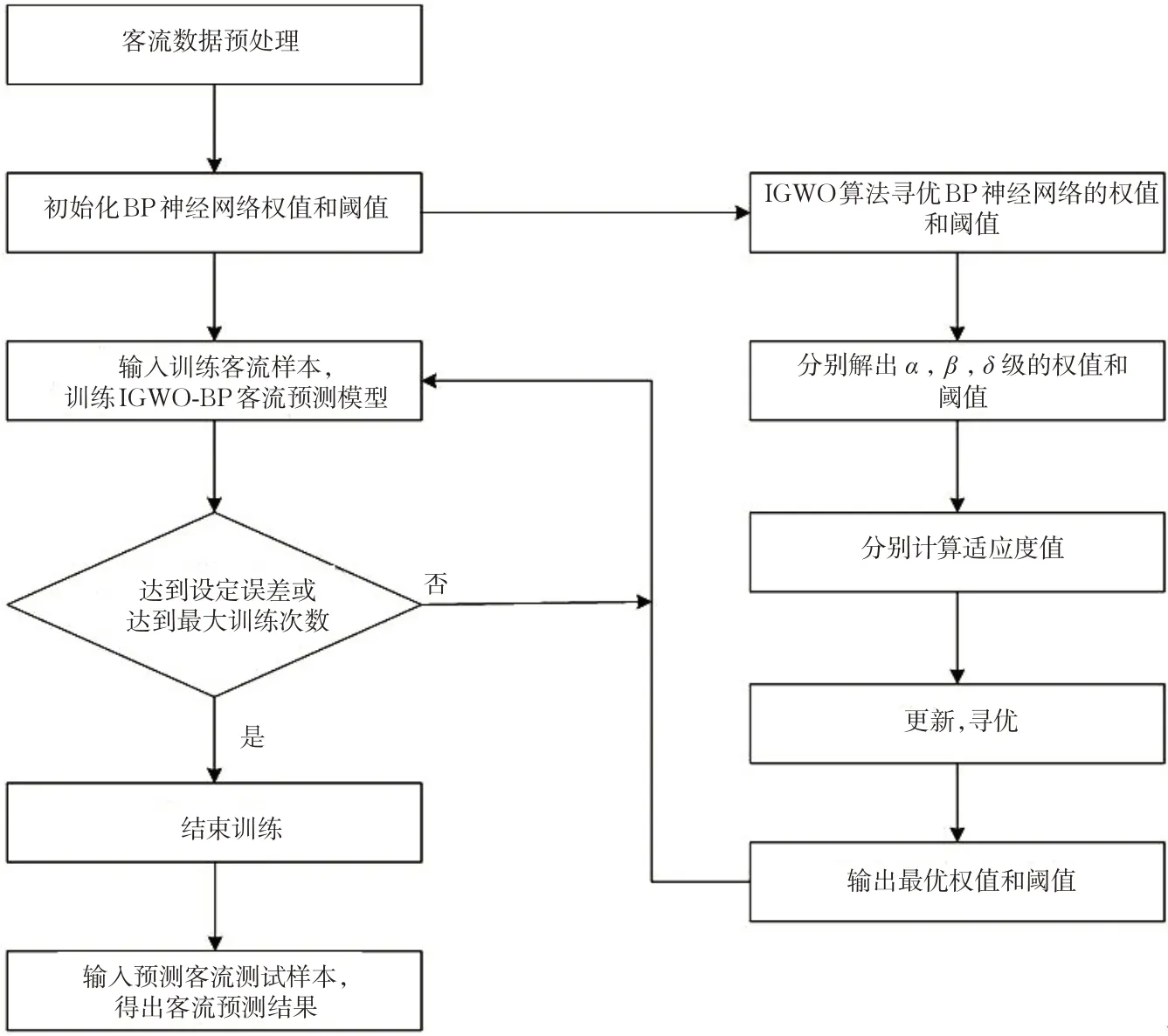
图2 IGWO-BP算法流程图Fig.2 Flow of the IGWO-BP algorithm

2.1 原始数据预处理

轨道交通短时客流预测所用的原始数据一般来源于AFC刷卡数据。若出现信号波动或机器故障，就会导致AFC传输错误，造成部分数据缺失或滞后。因此，对原始数据做如下处理。

1）剔除原始数据中明显偏高或偏低的数据，对比分析客流随时间变化的趋势。

2）相关系数是研究变量之间相关程度的量。对有相同趋势的客流数据做相关性分析，根据式（1）计算相关系数。

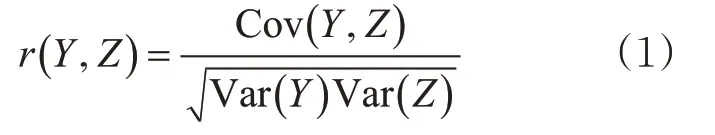
式中：r(Y，Z)为相关系数；Cov(Y，Z)为Y与Z的协方差；Var(Y)为Y的方差；Var(Z)为Z的方差。|r(Y，Z)|介于0～1之间，其值越接近1说明变量Y与Z的相关性越强。

2.2 适应度函数

在算法训练过程中，目标是轨道交通网络实际客流量与预测客流量误差最小[17]。即算法的适应度函数见式（2）。

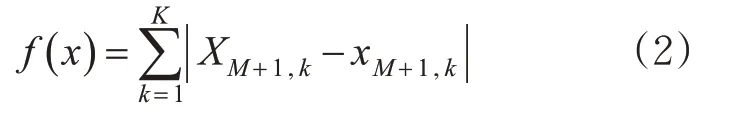
式中：X M+1，k和x M+1，k分别为第k个训练样本的客流量预测值和实际值，人次；K为样本的总数量。

2.3 IGWO算法寻优

在BP网络学习过程中，给每个连接权值和阈值赋予（-1,1）内的随机量来进行算法初始化，然后反向传播不断调整网络的权值和阈值，使网络的误差平方和最小，最终获得期望的结果[18]。当初始权值和阈值被赋予了不恰当的值，就会导致BP网络陷入局部最优，影响算法的效率。用IGWO算法优化BP网络的初始权值和阈值，就能够避免此种情况的发生。

2.3.1 GWO算法寻优

GWO算法寻找BP神经网络最优权值和阈值的过程即为灰狼寻找并捕获猎物的过程，见图3。将初始权值和阈值整体看作是灰狼种群，它们遵循α→β→δ→ω的等级制度。每代个体中适应度最好的权值和阈值标记为α，为种群的领导者；其次为β，负责协助α的工作；再次为δ，负责初始权值和阈值整体的侦查工作；其余为ω，负责完成高等级权值阈值交代的工作。最优权值和阈值即为α的值。

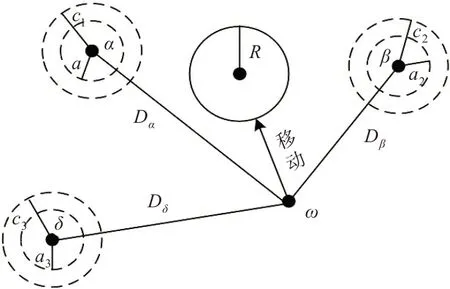
图3 GWO算法寻优过程Fig.3 Optimization process of the GWO algorithm

假设初始权值和阈值的总数为N，每个个体的位置为G={G1，G2，…，G N}，寻优过程中每个个体按照式（3）寻找目标。

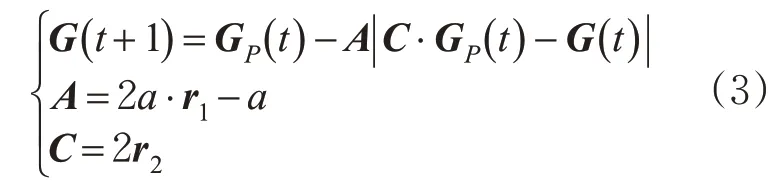
式中：t为迭代次数；G p(t)为目标在第t次迭代的位置；G(t)为个体在第t次迭代的位置；A，C为系数向量；r1，r2为标量在[0 ,1]之间的随机向量；tmax为最大迭代次数；a为收敛因子，它随迭代次数的增加从2线性减小至0，其表达式为

当 |A|＞1时，初始权值和阈值个体从候选解向外发散，来进行全局搜索，寻找其他潜在最优解；当|A|＜1时，初始权值和阈值个体从候选解向目标集聚，以进行局部搜索，逼近最优解。

初始权值和阈值寻找到目标后，各自按照式（5）～（6）逐步更新其位置靠近最优解。式（6）决定初始权值和阈值移动的方向。

经过多次迭代后，即可找到最优解。

2.3.2 原始灰狼优化算法的改进

通常，对于元启发式群智能优化算法，在其迭代过程的前期，应加强群体中个体的全局搜索能力；在迭代过程的后期，应增强算法的收敛能力[19]。在GWO算法中，全部搜索和局部搜索由A决定，而A的值由收敛因子a决定。根据式（3）可知，a由2线性递减至0的过程中，全局搜索与局部搜索约各占50%，将导致算法容易陷入局部最优。因此，引入余弦思想，对收敛因子a改进，其表达式见式（7）。

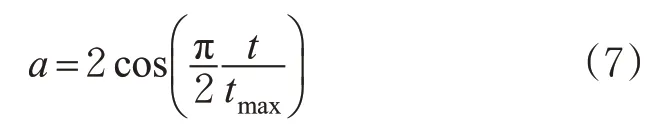
式（7）所示的收敛因子收敛曲线见图4，可以看出改进后的收敛因子大于1的时段明显多于线性收敛因子。使得算法在迭代前期，能提高寻找到全局最优解的可能性，在迭代后期，拥有更快的下降速度，局部搜索速度更快。

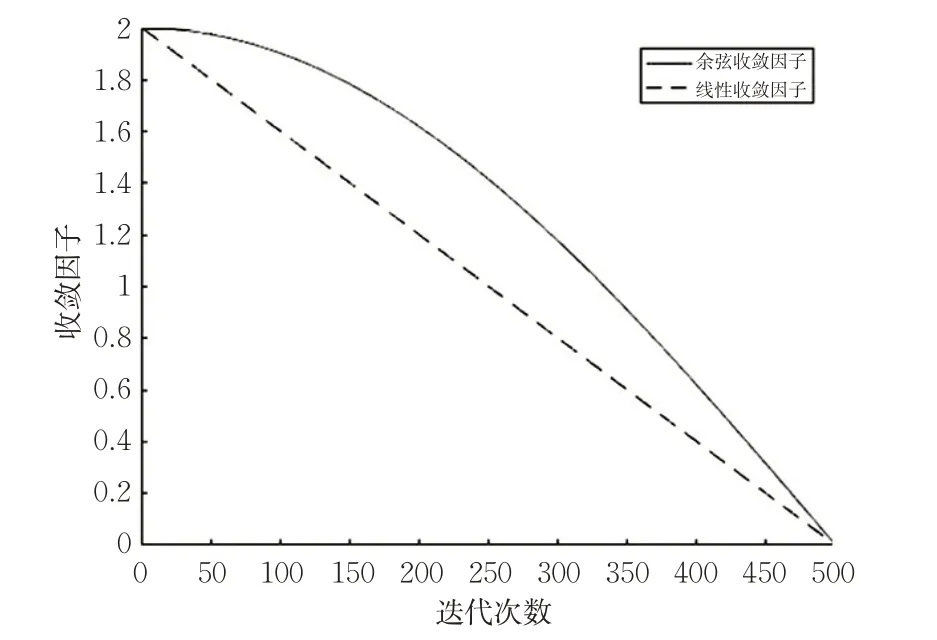
图4 收敛因子收敛曲线Fig.4 Convergence curve of convergence factors

在位置更新式（6）中，不同等级的权值和阈值均匀的影响着下一次的移动方向，但实际上，α，β，δ等级的权值和阈值在种群中的作用存在差异，因此，引入动态权重策略对其改进，其表达式见式（8）。

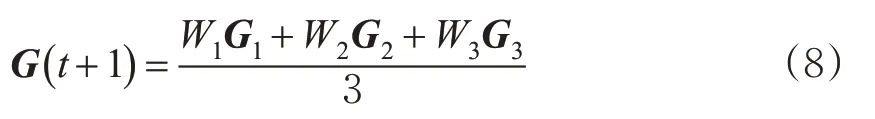
式中

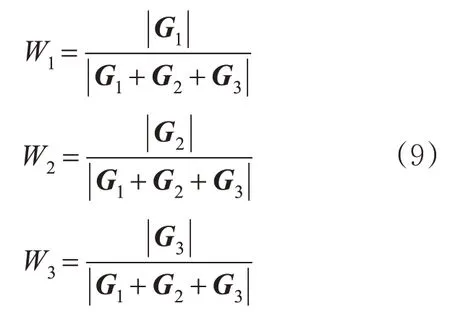
改进后，权值和阈值可根据权重对下1次的种群移动方向起作用，距离目标越近，作用越大。

IGWO算法寻找最优权值和阈值的步骤如下。

步骤1。种群初始化，设定种群规模N；最大迭代次数tmax；维度D；解空间上限ub；下限lb等。

步骤2。初始化参数a，A，C。

步骤3。计算每个种群个体的适应度，将适应度最好的3个个体依次标记为第1代α，β，δ。

步骤4。判断是否达到最大迭代次数，若没有达到最大迭代次数，转步骤5；若达到最大迭代次数，转步骤9。

步骤5。计算每个权值和阈值的位置。

步骤6。更新参数a，A，C。

步骤7。计算当前所有权值和阈值的适应度，若当前候选解的适应度值高于最优解，则替换最优解。

步骤8。更新Gα，Gβ，Gδ，转步骤4。

步骤9。输出最优解Gα。

2.4 评价指标

本文采用平均绝对误差MAE、均方根误差RMSE、平均绝对百分比误差MAPE这3个指标对算法的预测结果进行评价。其计算公式见式（10）～（12）。

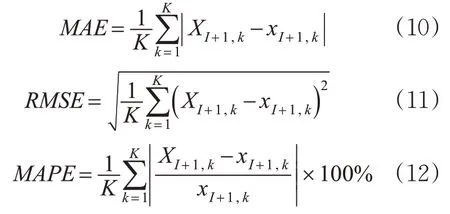
式中：X I+1，k和x I+1，k分别为第k个测试样本的客流量预测值和实际值，人次；K为样本的总数量。MAE，RMSE，MAPE都是用来度量预测误差的量，其值越小，预测性能越好。

3 实例分析

本文选用来源于西安市轨道交通2号线龙首原站2019年11月1日—12月31日早高峰07:00—09:00时间粒度为15 min的进站客流数据，本次共得到488组数据。

剔除不合理数据后，随机挑选包含工作日与非工作日在内的客流数据进行对比，结果见图5。可以发现工作日与非工作日呈现不同的客流趋势，其中工作日的客流走势大致相同，非工作日的客流走势大致相同。利用式（1）对相同工作日客流矩阵进行相关性分析，表1为同1 d工作日不同时段客流量相关系数计算结果，表2为同1 d工作日相同时段客流量相关系数计算结果。可以发现，表2数据相关性更高，达0.96，说明用相同时段的历史客流量做预测精度更高，实用性更强。

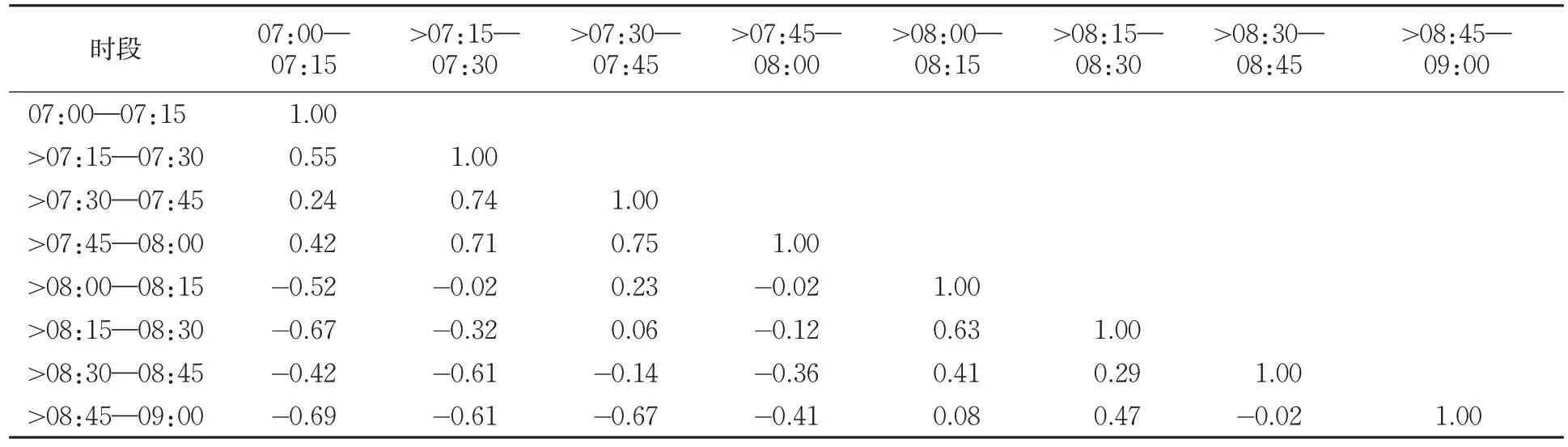
表1 同1 d工作日不同时段客流量相关系数Tab.1 Correlation coefficient of the passenger flow at different time of the same working day

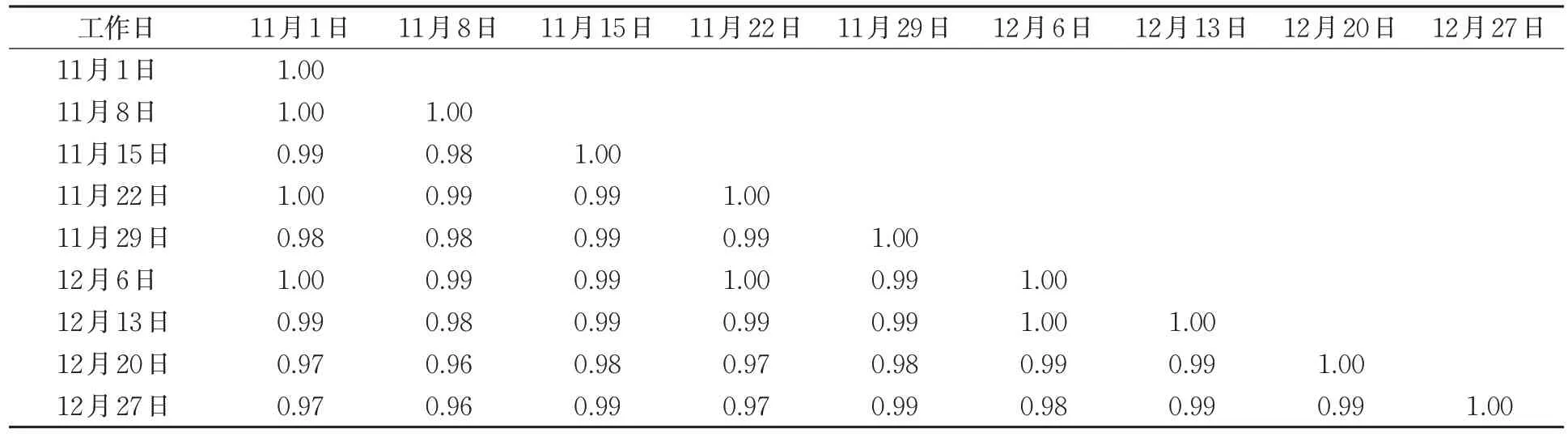
表2 同1 d工作日同一时段客流量相关系数Tab.2 Correlation coefficient of the passenger flow at the same time of the same working day

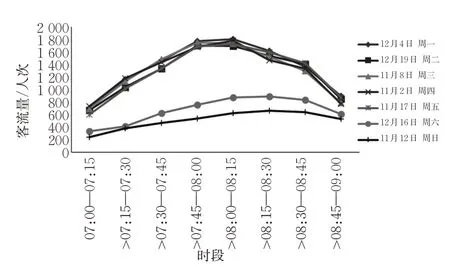
图5 不同日期进站客流量对比Fig.5 Comparison of the inbound passenger flow on different days

使用Matlab 2016a软件编写程序进行客流预测。选取9个周三的客流数据，将前8个周三的数据作为训练集，预测第9个周三相同时段的客流量，并与第9个周三的实际进站客流量对比验证。BP网络拓扑结构为3-9-1，隐含层和输出层均选用tansig函数传递，训练函数选用traindx。训练次数为10 000，学习速率为0.01，目标误差为1/10 000。IGWO算法的种群规模为N=30，搜索空间维度为D=46，最大迭代次数为tmax=30。IGWO-BP算法的最优权值和阈值计算值见表3。

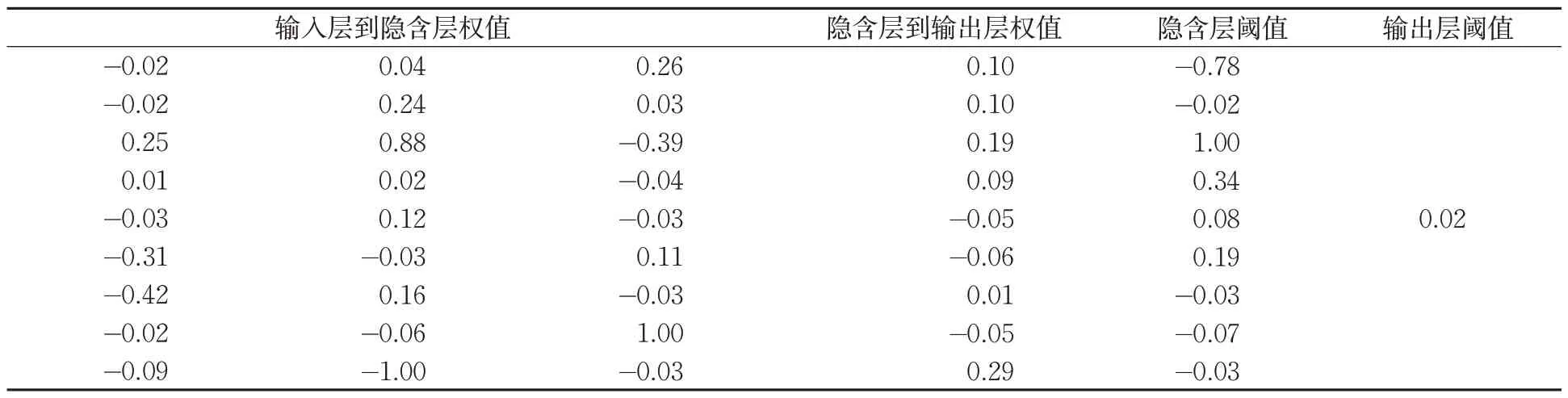
表3 IGWO-BP算法权值和阈值计算值Tab.3 Calculated values of the weight and threshold of the IGWO-BP algorithm

将上述数据输入本文构建的IGWO-BP算法，运行20次，最优1次的预测结果和预测结果的平均值见图6。可知：IGWO-BP算法最优1次预测值与平均值的客流量走势基本一致，且预测值更接近真实值。IGWO-BP算法多次预测结果见图7。IGWO-BP算法同一时间段的多次预测值都集中在某1个值的附近，说明采用IGWO算法优化BP网络的权值和阈值后，预测结果稳定性有了很大提升。在IGWO-BP算法的多次预测结果中均出现了第5个时间段（08：00—08：15）和第6个时间段（08：15—08：30）的预测值远小于实际值，第7个时间段（08：30—08：45）的预测值远大于实际值的情况，这是因为神经网络只能根据输入数据的特点进行预测，而短时客流具有较强的随机性，前8个周三这3个时间段的客流量与第9个周三的客流量相差过大，说明IGWO-BP算法学习能力强，适应性好。

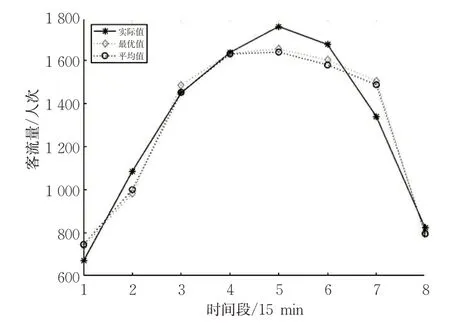
图6 IGWO-BP算法预测结果最优值和平均值Fig.6 Optimal and average values of predicting the IGWO-BP algorithm

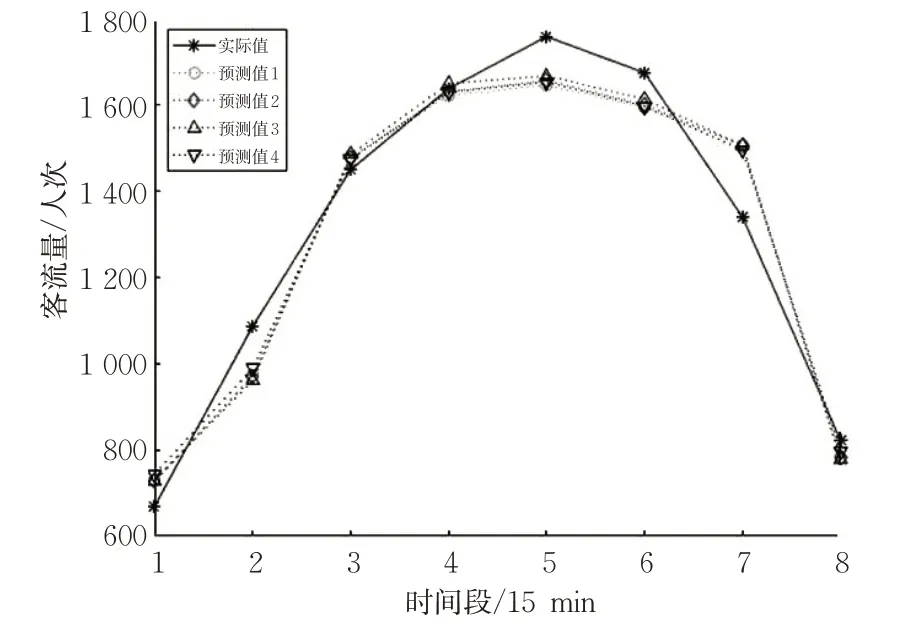
图7 IGWO-BP多次预测结果对比Fig.7 Predicting results of the IGWO-BP algorithm

根据式（5）～（7）计算IGWO-BP算法预测结果的评价指标见表4，RMSE的平均值为89.65，MAPE的平均值为1.16%，标准差为0.01，说明该算法对于短时客流预测可以取得较高的精度，算法的稳定性强。

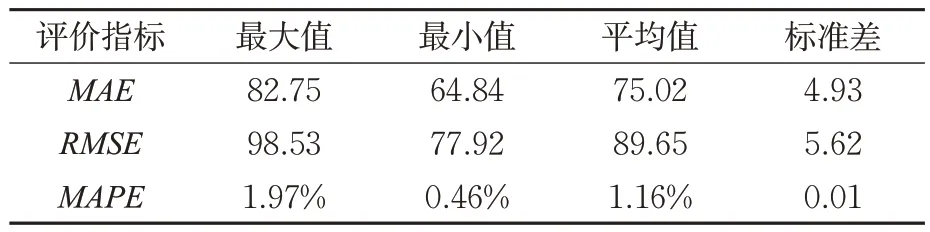
表4 IGWO-BP算法预测结果评价指标Tab.4 Evaluation of the forecast results of the IGWO-BP algorithm

为了验证IGWO-BP算法的有效性，将IGWO-BP的预测结果与其他几种常用的短时客流预测模型进行比较。对比的模型包括卡尔曼滤波（KF）、灰色模型（GM）、支持向量机（SVM）、BP神经网络（BPNN）、原始灰狼算法优化的BP神经网络（GWO-BP）。龙首原站不同模型的短时客流预测结果见图8。从图中可以看出，KF和GM的预测结果较差，SVM、BPNN、GWO-BP、IGWO-BP预测结果的走势相近，IGWO-BP的预测结果与实际值的拟合度最高，准确度最好。

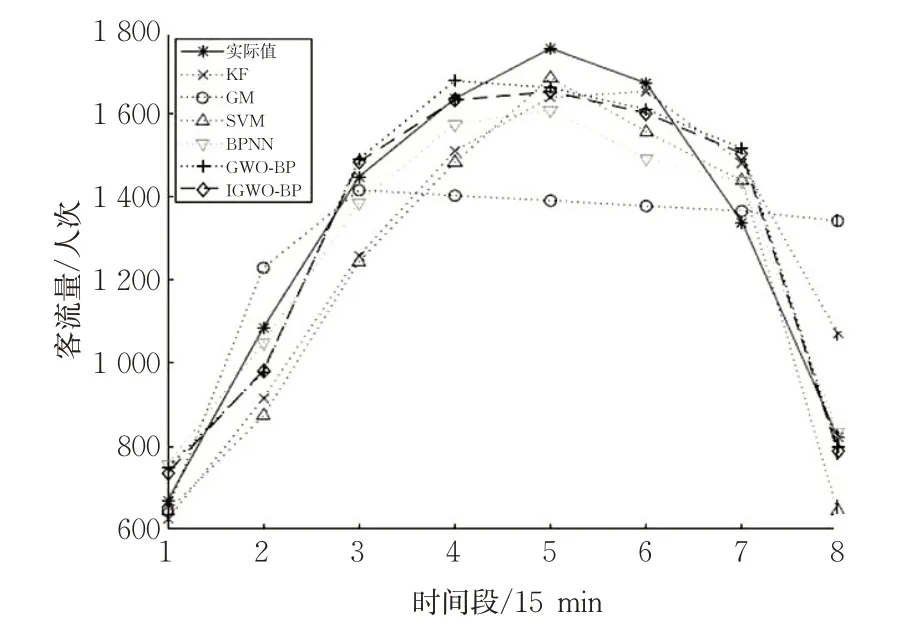
图8 不同模型预测结果对比Fig.8 Comparison of the predicting results of different models

为了准确反映不同模型的预测性能，计算不同模型预测结果的评价指标见表5。表5中数据显示，IGWO-BP算法的各项指标计算结果均小于其他模型，说明IGWO-BP的预测结果最准确。与其他模型相比，IGWO-BP算法预测结果的准确度提升了8.29%，稳定提升了6.45%。KF和GM的预测结果与实际客流量相差较大，是因为KF和GM是参数型预测模型，不适用于非线性和随机性较强的短时客流预测问题。SVM和BPNN可以学习线性关系，但由于其需要大量的原始数据作为支撑，预测效果精度不高。GWO-BP能够得到相对较好的预测结果，但需多次运行，且每次的预测结果稳定性不强。IGWO-BP算法由于引入了余弦思想和动态权重策略，能够很好的适用于非线性关系，预测结果精度高，算法多次运行结果稳定。

表5 预测结果评价指标对比Tab.5 Comparison of evaluation indices for predicting results

4 结束语

轨道交通短时客流预测能够为交通运营管理提供重要参考。本文利用BP神经网络能学习和存储大量的输入/输出模式映射关系而无需事前揭示描述这种映射关系的数学方程的优点来预测短时客流量，并对基本灰狼算法的收敛因子和位置更新公式进行改进，引入改进的灰狼优化算法（IGWO）优化BP网络的权值和阈值，提高BP网络的预测精度和稳定性。

实例验证结果显示，与传统的客流量预测方法相比，采用IGWO优化BP神经网络的权值和阈值，不需要复杂的公式计算，只需同期历史数据即可进行预测，并且在预测精度和稳定性方面均获得了良好的效果。将IGWO-BP算法的预测结果与常用的几种短时客流预测模型（KF、GM、SVM、BPNN、GWO-BP）比较，表明与其他模型相比，IGWO-BP算法具有最高的精确度和稳定性，评价指标也是最优。

短时客流量具有非线性和随机性的特点，极易受天气、突发大型事件等的影响而发生变化，并且在不同空间分布也有很大差别。下一步将在此问题上进一步研究。