灵活多车场多类型的叫车接送问题的规划模型*

陈可嘉 方云飞 骆佳艺

（福州大学经济与管理学院 福州350116）

0 引言

叫车接送运输（dial-a-ride transportation，DART）是指乘客打电话到运营中心告知其接送需求（包括接送起点和终点）后，运营中心的调度员根据乘客预约信息规划路线，并指派车辆接送用户，完成接送任务的面向预约的运输方式[1-2]。这种运输方式作为公共交通运输的1种补充形式，主要是为行动不便的老年人和残疾人设计门到门的接送服务，所使用的车辆配备有轮椅坡道或者轮椅升降机，车内除了正常的座位，还配有担架位、轮椅位，以满足乘客的不同需求，为他们的出行提供便利。随着老年人口比例逐年上升，以及医疗保健服务不断发展，叫车接送运输的需求量日益增长。考虑到运输对象多为特殊群体，为了设计合适的运输路线以避免用户就医延误、实现高质量的服务，过去40年来，叫车接送问题（Dial-a-ride Problem，DARP）已经被研究人员广泛探讨[3]。

DARP是车辆路径问题（vehicle routing problem，VRP）的延伸。然而，DARP不同于VRP及其扩展问题，因为DARP涉及到人而不是货物的运输。DARP满足乘客给定接送起点和终点的接送需求，并且可同时服务多名乘客。因此，DARP关注乘客在特殊要求下出行服务的高水平高质量。一般情况下，DARP旨在最大限度地降低车辆运营成本（主要与车辆行驶成本相关），同时达到乘客可接受的服务水平（主要包括服务时间窗要求、位置资源要求和乘坐时间限制等）。

尽管DARP是1个NP-hard问题，但目前学者对这个问题已经进行了诸多研究，大量的启发式方法被提出并广泛应用于这个问题。孙博等[4]针对随机正态分布乘客需求的DARP问题，提出基于集对分析的调度方法，得到较好的结果。孙继洋等[5]设计了基于引力模型的启发式算法，有效解决了考虑乘客动态需求的DARP问题。Parragh等[6]分析了多车型DARP问题，提出了1种基于变邻域搜索的启发式算法。Häme[7]设计了1种自适应插入启发式算法，有效解决了只考虑单一车辆的DARP。Parragh和Schmid[8]针对DARP提出了1种高效的混合算法，将变邻域搜索（variable neighborhood search，VNS）集成到列生成中，并将其与大邻域搜索（Large Neighborhood Search，LNS）相结合，在较短的计算时间内得到了较好的结果。Muelas等[9]给出了1种用于处理大城市或人口稠密地区中常见的大规模情景DARP问题的分布式VNS算法，并在旧金山市进行测试，得到了较好的结果。Ritzinger等[10]考察了带时间窗的DARP问题，提出了1种基于动态规划思想的元启发式算法，并将其集成到大邻域搜索框架中。Tripathy等[11]基于改进蚁群优化算法来研究多车型DARP问题。Masmoudi等[12]设计了1种混合遗传算法，为不同类型用户、多车型车队规划车辆路径。关于解决该问题的精确算法，文献中很少出现。Cordeau[13]针对DARP设计了精确的分支切割算法，并且求解了多达4辆车和48个出行需求的实例。基于Cordeau的研究，Ropke等[14]建立了1个新的模型，减少了变量和约束的数量，求解了多达8辆车和96个出行需求的DARP实例。Liu等[15]同样采用了分支切割方法，解决了1个实际生活中的叫车接送问题，同时考虑了多次出行，多类型车辆，多类型需求等因素。

近年来，越来越多的实际限制因素被学者们考虑并进行DARP研究，不同类型的车辆[16-18]，如多个车场[19]，和乘客需求等[20-21]。但之前关于DARP的文献中普遍都有1个假设，即每辆车结束工作的车场与开始工作的车场必须相同。Kek等[22]首次提出灵活车场的概念，即允许车辆自由在任何车场开始和结束其路线，并将其考虑进车辆路径问题的研究中。实验证实引入灵活车场假设的车辆路径问题的行驶成本比固定车场车辆路径问题的行驶成本最多可降低近50%。Markov等[23]考虑了1个带灵活车场的垃圾回收车辆路径问题，通过对现实案例的测试，实验表明允许车辆灵活返回车场能够将车辆行驶距离平均节约14.6%。

灵活车场是1种在实践中较少出现的情况，因此在大多数研究中常常被忽略。然而，合适地使用这种灵活性，允许车辆结束任务车场不同于开始工作车场，可以显著地节约车辆行驶成本。基于此，笔者在现有研究的基础上引入灵活车场的假设，研究了1个新的DARP扩展问题——灵活多车场多类型的叫车接送问题（Multiple Depots Heterogeneous Dial-a-ride Problem with Flexible Depots，MDHDARP-FD），以总行驶成本最小为目标，构建了MDHDARP-FD的混合整数非线性规划数学模型。为使该模型易于求解，对原模型进行约束线性化、变量聚合和添加有效不等式等处理，形成1个新的线性规划模型，并利用数学规划求解器CPLEX进行求解。通过典型算例以及系列算例的测试，验证了该模型的有效性。

1 问题描述与模型建立

1.1 问题描述

MDHDARP-FD旨在设计1组车辆路线以满足一定数量的接送需求。每个需求包括到指定的出发地接乘客并将其送至指定的目的地。乘客可能在出发地或者目的地指定时间窗，要求在时间窗内被服务。如果车辆太早到达，就得等到时间窗的开始时间才能开始服务。另外，MDHDARP-FD还需要满足一系列约束，比如车辆行驶时间，乘客乘车时间，车辆位置资源等。目标是最小化所有车辆的总行驶成本。

本文中，MDHDARP-FD作为标准DARP的扩展问题，在DARP基础上考虑了多车场和多类型。其中，多类型是指使用的车辆上配备有多种位置资源类型（例如常规座位、轮椅位、担架位）和接送的乘客具有不同位置资源需求类型。另外，与现有文献中的标准DARP和一些扩展问题不同，MDHDARP-FD假设具有灵活车场，即车场对所有车辆开放，每辆车可以在不同的车场开始和结束其路线。只要能使成本最小化，每辆车可以在任何车场停止其路线。通过引入车辆结束路线时返回车场的灵活性，可以减少其行驶时间和叫车接送服务的总运营成本。

传统的DARP问题中，假设有1个同类型车辆构成的车队，所有车辆都有相同的用户承载量，并且往返于单一车场，接送单一类型的用户；与传统的DARP问题相比，MDHDARP-FD考虑更为一般的情形，包括多个车场，多类型用户，每个用户不同的资源需求（例如常规座位和轮椅位置），相应的车队拥有不同类型车辆，每辆车配备不同类型及数量的资源。

1.2 符号说明

集合和参数。

V：点集，V=M∪P∪D∪M’，其中M和M’分别表示出发车场和返回车场的集合，P和D分别表示乘客需求起点和需求终点的集合。

A：弧集。

R：车辆位置资源集合。

K：车辆集合。

C rk：车辆k上配备位置资源r的数量。

：节点j对位置资源r的需求数量。

L：乘客最大乘车时间。

T k：车辆k的最大行驶时间。

si：节点i的服务时间。

[ei，l i]：节点i的服务时间窗。

cij：从节点i到节点j的行驶成本。

tij：从节点i到节点j的行驶时间决策变量。

：车辆k经过弧（i，j）时为1，否则为0。

：车辆k在节点i的开始服务时间。

：离开节点i时车辆k上位置资源r的使用量。

1.3 模型构建

基于上述参数和决策变量，建立MDHDARP-FD的混合整数非线性规划模型P0见式（1）～（16）。

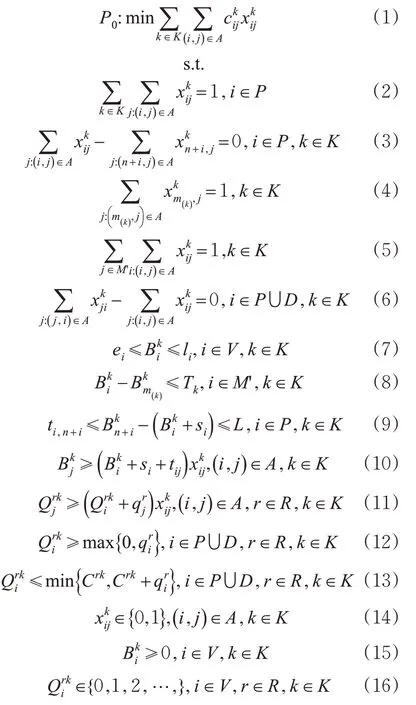
上述模型中，式（1）为目标函数，表示最小化所有车辆的总行驶成本；式（2）～（3）确保每个乘客被服务的次数只有1次，并且每个乘客的起点和终点由同1辆车服务；式（4）～（6）限制每辆车k从车场m(k)出发，并在服务结束时可以返回到任意1个车场；式（7）表示每个需求节点的时间窗约束；式（8）和式（9）分别表示每辆车的最大行驶时间约束和每个乘客的最大乘车时间约束；当车辆k经过弧（i，j）时，式（10）和式（11）分别定义了节点j的开始服务时间和离开节点j时车辆位置资源的使用量；式（12）～（13）表示车辆位置资源使用量约束；式（14）～（16）分别定义了0-1整数决策变量、非负连续型决策变量和非负整数决策变量。

与传统的DARP模型相比，约束式（4）和式（5）在传统DARP问题中每辆车到达路线终点后需返回出发车场上的基础上，使每辆车可以在不同的车场开始和结束其路线；约束式（7）和式（8）除了设置乘客需求起点和需求终点的集合外，还包括了出发车场和返回车场的集合，使得车辆的路线具有灵活性；约束式（16）使车辆上配备的位置资源类型多样化，并满足接送乘客的不同位置资源需求类型。

2 模型重构

上述MDHDARP-FD问题考虑了多个车场、多类型位置资源和乘客需求，并且假设车辆可以在服务结束时回到任何1个车场，比标准的DARP更复杂。因此，想要直接求解原模型P0是非常困难的。为了使MDHDARP-FD易于求解，本文对P0模型进行重构，进行了约束线性化、变量聚合和添加有效不等式等处理，获得1个新的模型。

在约束线性化过程中，非线性约束被重写为等价的线性约束，因此原模型转化为线性规划模型。在变量聚合过程中，本文将具有相同性质的决策变量进行聚合，以减少变量数量，降低问题规模。此外，还引入了一些有效不等式来强化模型。上述重构过程参考了文献[19]中提到的方法。详细描述如下。

2.1 约束线性化

在模型P0中，约束式（10）和式（11）是非线性的，因此P0不能直接使用线性规划求解器进行求解。为此，本文引入了1个很大的正数M来线性化这2个约束。

以约束式（10）为例，当车辆k经过弧（i，j）即=1时，我们有≥+si+t ij，否则约束（10）不起作用。因此，约束式（10）可以重写为

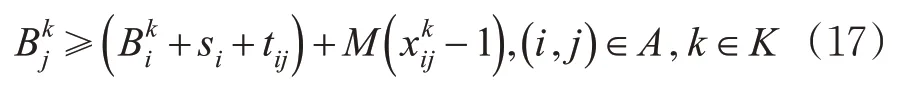
式中：M为1个很大的正数。

同样的，车辆位置资源的使用量约束（11）可以重写为

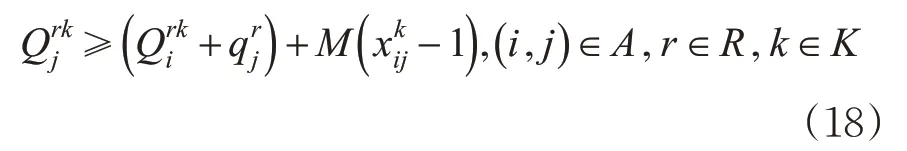
通过引入1个很大的正数M，将非线性约束式（10）和式（11）可以分别由等价线性约束式（17）和式（18）代替，原模型也转换为线性规划模型，并且新的线性规划模型的解与原模型解一致，从而使得线性规划求解器能够求解本文问题。

2.2 变量聚合

根据前面MDHDARP-FD问题的描述，每个需求节点（需求起点或需求终点）只被1辆车访问1次，那么所有与车辆无关的服务时间变量都可以用1个简单的变量代替。具体来说，对1个固定的节点i∈P∪D，所有k∈K的都可以被变量Bi代替。因此，时间窗约束式（7）可以等价于约束式（19）～（21）。

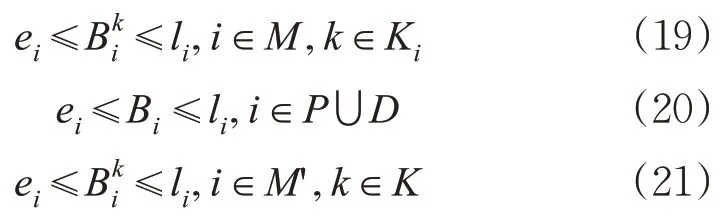
式中：Ki为位于出发车场i的车辆集合。因为需求节点i∈P∪D只可能被1辆车经过1次，而车场i∈M∪M'可能被多辆车经过，因此在式（20）中使用聚合后的变量Bi，在式（19）和式（21）中仍然使用以区分不同的车辆。

类似的，约束式（9）和式（10）可以分别替换为式（22）和式（23）～（25）。

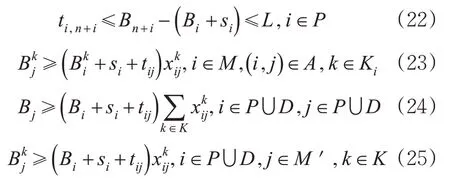
另外，式（23）～（25）可以用2.1描述的方法进一步转化为线性约束。

通过聚合除出发车场和终点车场之外每个节点上的时间变量，可以减少整个MDHDARP-FD问题中变量和约束的数量，模型的复杂性大大降低。

2.3 有效不等式

尽管原模型P0已经转化为线性规划模型，并且随着变量聚合，决策变量和约束的数量都减少了，但是求解MDHDARP-FD仍然是困难的。为了有效地解决这个问题，引入多个不等式来减少所考虑问题的搜索空间。

如果1辆车经过弧（j，i），由于j点时间窗下界为e j，最早到达i点时间为e j+d j+t ji，那么最早服务i点的时间为e j+d j+t ji或ei，具体取决于二者的大小。当到达i点时间e j+d j+t ji小于i点时间窗下界ei，则需要等待至ei才开始服务；当到达i点时间e j+d j+t ji大于i点时间窗下界ei，则无需等待。考虑到每1个节点i∈P∪D只能被1辆车经过，因此时间窗下界可以强化为约束式（26）。

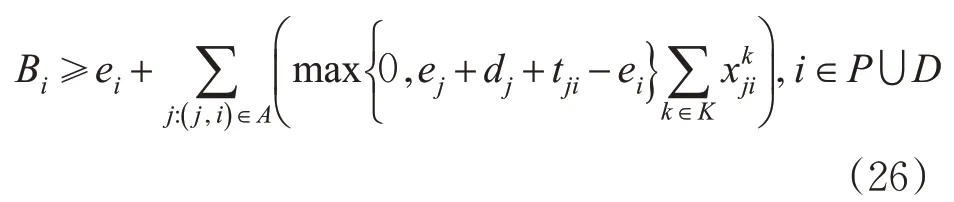
通过考虑反向弧，时间窗上界可以强化为约束式（27）。

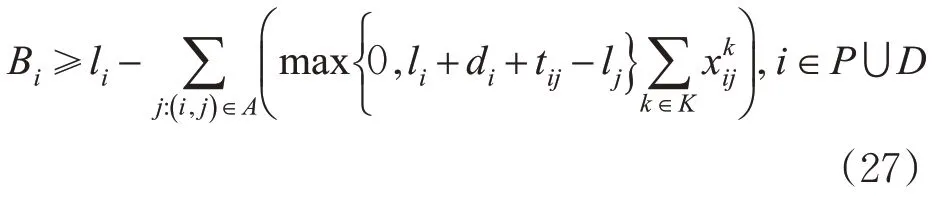
同样的，位置资源的使用量的下界也可以强化为约束式（28）。

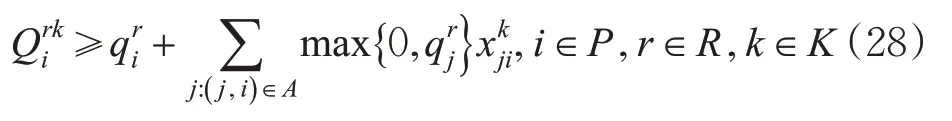
通过引入多个有效不等式，能够进一步收紧时间窗的上下界窗口，强化不同车辆在弧（j，i）上的优先关系，并确保同1个请求的2个节点在同1条路线上。

3 算例分析

为了验证上述模型的有效性，本文选取文献[19]中提供的datasetU和datasetE这2组算例进行测试。2组算例来源于奥地利格拉茨市红十字会在病人运输领域的真实情况，在接送老年人和残疾人的情况下，一些乘客可能要求坐轮椅接送，而另一些乘客可能使用常规车辆座位；在运送病人的情况下，乘客可能需要用担架运送。其中，datasetU组算例考虑单一类型的位置资源和乘客需求，datasetE组算例引入了4种位置资源类型，并且不同的乘客对这4种位置资源的需求不同。所选用的算例中车辆数量范围为2～4辆，乘客需求数量范围为16～30个。与文献[19]类似，我们在实验时假设有4个车场（坐标分别为[-5，-5]，[5，5]，[-5，5]，[5，-5]），可用车辆最初分布于不同车场，第1辆车安排到第1个车场，第2辆车安排到第2个车场，以此类推。与文献[19]不同的是，MDHDARP-FD假设车辆具有灵活车场，即车场对所有车辆开放，每辆车可以在任何车场结束其路线。

本文借助数学规划求解器CPLEX12.6.3，在Intel Core i5 2.50GHz处理器、8GB内存、Windows 7系统的电脑上运行求解。

3.1 典型算例实验与结果分析

以datasetE组算例中的Ea4-16作为典型算例进行实验。算例Ea4-16中有4辆车，需要完成16个乘客的接送需求。4辆车分别位于[-5，-5]，[5，5]，[-5，5]，[5，-5]这4个车场。每辆车上配备有3个常规座位（其中1个员工座位、2个病人座位）、1个担架位、1个轮椅位。车辆最大行驶时间为240 min。

乘客需求信息见表1。每个乘客需求包含1个需求起点和1个需求终点。序号1～16为乘客需求起点的信息，序号17～32为对应的需求终点信息。所有的点在[-10，10]2的欧式平面随机生成。其中一半的需求在起点设时间窗，一半在终点设时间窗。时间窗长度为15 min。每个需求节点（需求起点或需求终点）的服务时间为3 min，乘客最长乘车时间为30 min。不同的乘客对4种位置资源的需求不同。

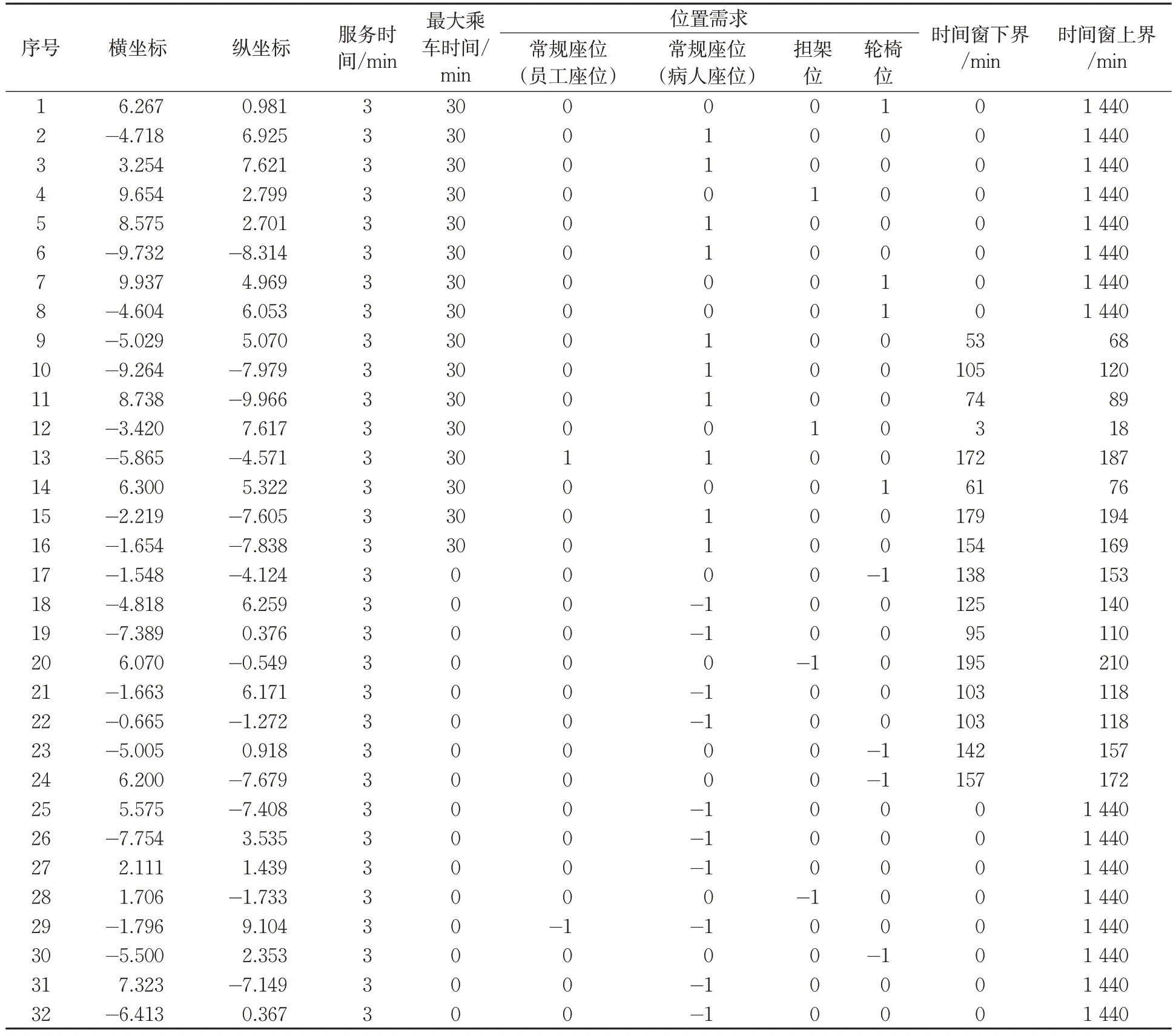
表1 算例Ea4-16的乘客需求信息Tab.1 Passengers'demand information of Example Ea4-16

对于上述典型算例，混合整数非线性规划模型重构后共有20 385个约束条件，3 852个变量，其中3 780个整数变量。运用CPLEX进行求解，用时1 661.44 s，主要结果见表2。根据求解结果绘制出车辆接送路线，见图1，相应的最优接送路线列于表3中。

表2 算例Ea4-16的模型求解结果Tab.2 Model solution results of Example Ea4-16

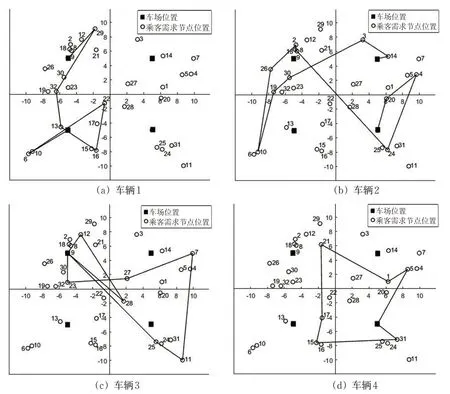
图1 算例Ea4-16的车辆接送路线图Fig.1 Route for vehicles of Example Ea4-16

表3 算例Ea4-16的最优接送路线Tab.3 Optimal route of Example Ea4-16

从算例结果可以看出，本文所建立的模型能在满足车辆行驶时间约束、乘客乘车时间约束、车辆位置资源约束、时间窗约束等的基础上，得到1组实现乘客接送需求的最优车辆路线。并且，由图1（d）和表3可知，车辆1和车辆2在接送结束后并没有返回其出发车场，而是返回距离接送结束点最近的车场，能够减少车辆的行驶时间，从而使得所有车辆总行驶成本更小。

3.2 系列算例实验与结果分析

本文从文献[19]提供的Dataset U和Dataset E这2组算例中各选取8个算例进行实验，并将求解结果与文献[13]、文献[17]和文献[19]的结果进行比较（见表4）。表4中“MDHDARP-FD”列、“MD-H-DARP”列、“H-DARP”列、“2-index-DARP”列和“DARP”列分别表示本文MDHDARP-FD的最优值、文献[19]中MD-H-DARP的最优值、文献[17]中H-DARP和2-index-DARP的最优值和文献[13]中“DARP”的最优值。“G1（%）”列“、G2（%）”列、“G3（%）”列和“G4（%）”列分别给出了MDHDARP-FD和MD-H-DARP、H-DARP、2-index-DARP和DARP最优值之间的差距。另外，表4中还给出了MDH-DARP-FD以s为单位的计算时间，用CPU表示。

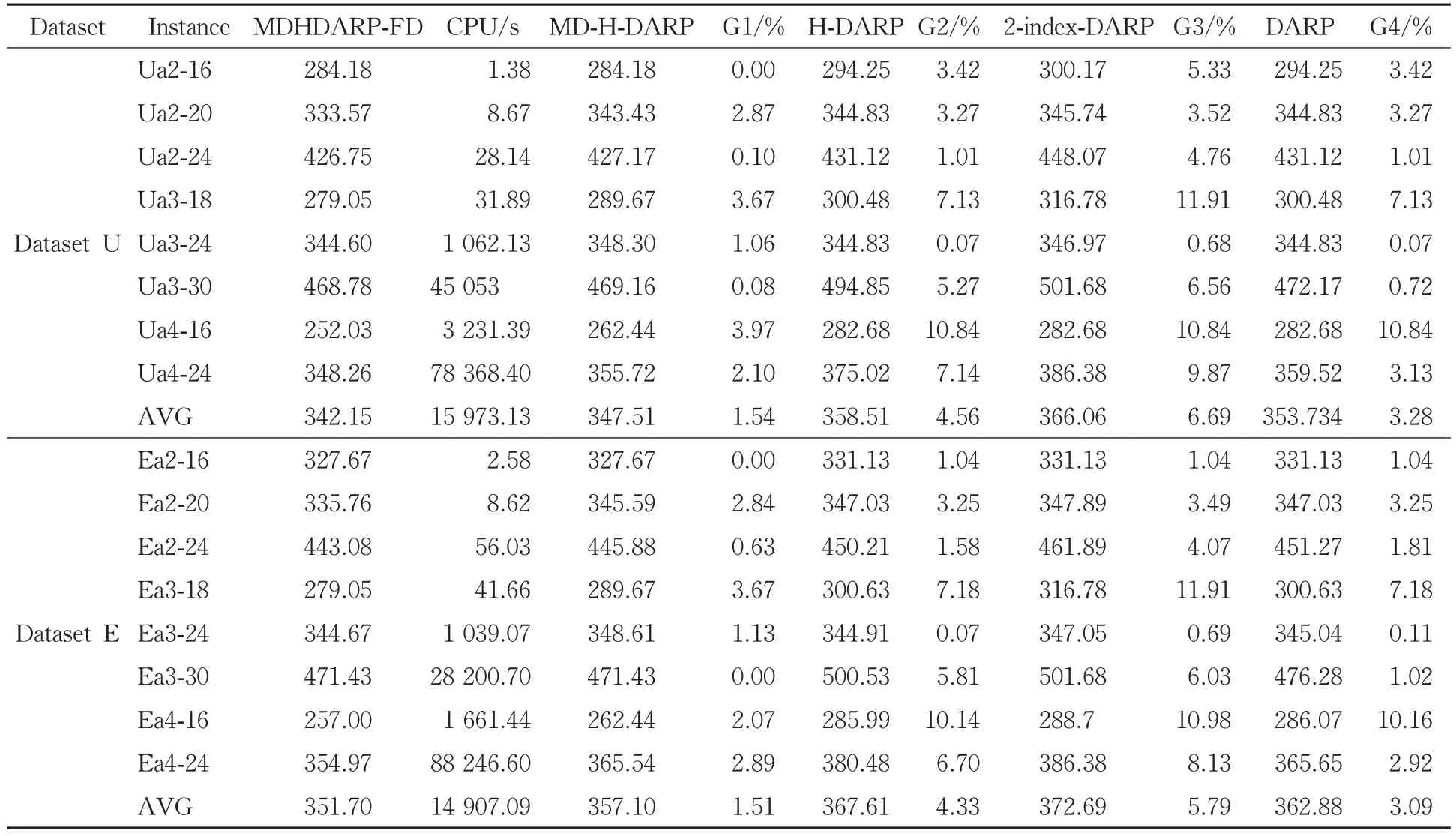
表4 系列算例求解结果及比较Tab.4 Comparison results of examples

从表4可以看出，对于所有的测试算例，MDHDARP-FD的最优值都小于MD-H-DARP、H-DARP、2-index-DARP和DARP的最优值，这意味着叫车接送服务的总行驶成本可以随着灵活车场的引入而减少。对于具有单一类型的情况（Dataset U），MDHDARP-FD较MD-H-DARP总行驶成本平均降低1.54%，较H-DARP平均降低4.56%，而平均需要15 973.13 s才能获得最优解。对于具有多类型的情况（Dataset E），MDHDARP-FD较MD-H-DARP和H-DARP的总行驶成本分别平均下降1.51%和4.33%，平均运行14 907.09 s得到最优解。值得注意的是，MDHDARP-FD最优解与H-DARP最优解之间的差距可以达到10%以上，例如Ua4-16和Ea4-16。

4 结束语

本文研究了DARP的1个新的扩展问题MDHDARP-FD，首次将灵活车场引入叫车接送问题，并以总行驶成本最小为优化目标，构建MDHDARP-FD的混合整数非线性规划模型。为使该模型易于求解，进行一系列降低原模型复杂度的处理，如约束线性化、变量聚合、添加有效不等式等措施，从而获得1个解空间较小的新线性规划模型。最后，通过典型算例以及一系列标准算例验证了模型的有效性，证实了叫车接送服务的总行驶成本可以随着灵活车场的引入而减少。由于MDHDARP-FD问题是1个NP-Hard问题，当问题规模增大时，难以利用精确算法来快速求解。因此，在未来的研究工作中，我们将设计基于禁忌搜索、领域搜索等智能算法框架的高效问题解决方案，以在可接受的计算时间内获得高质量的问题近似解。。